3.1.4: Viscosity

Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. Every single fluid inherently has viscosity. The less viscous the fluid is, the easier is the movement (fluidity). For instance, it is well known that the honey has low fluidity (high viscosity), while water presents, compared to honey, high fluidity (low viscosity). Viscosity is a property of the fluid, but affects only if the fluid is under movement. Viscosity describes a fluid’s internal resistance to flow and may be thought as a measure of fluid friction. In general, in any flow, layers move at different velocities and the fluid’s viscosity arises from the shear stress between the layers that ultimately opposes any applied force.

Viscosity stress

The viscosity force is a friction force and therefore the shear stress \(\tau\) (viscosity stress) is a force over a unity of surface.

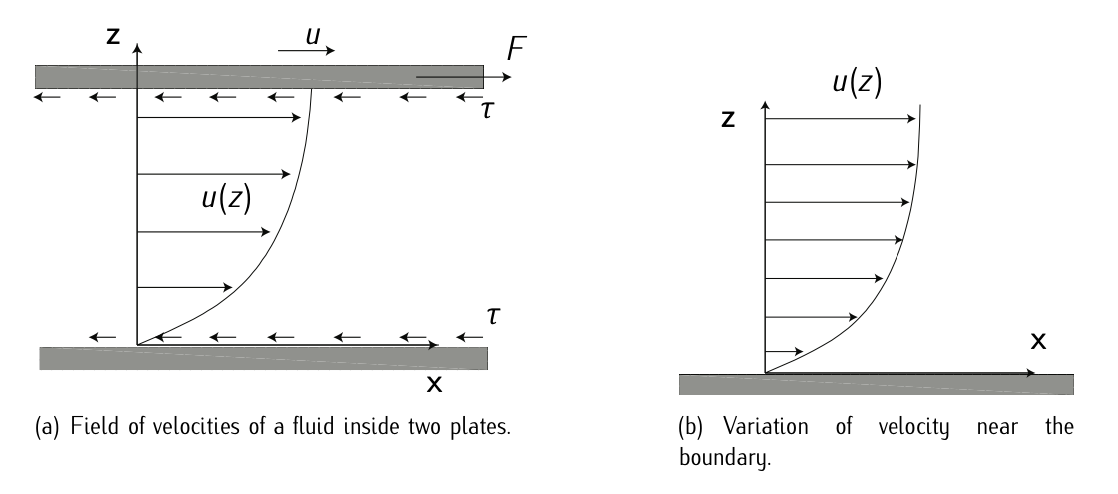
Figure 3.5: Viscosity. Adapted from \(F_{\text{RANCHINI}}\) et al. [4]

The relationship between the shear stress and the velocity gradient can be obtained considering two plates closely spaced at a distance \(z\), and separated by a homogeneous fluid, e.g., water or oil. Assuming that the plates are very large, with a large area \(A\), and that the lower plate is fixed, let a force \(F\) be applied to the upper plate. Thus, the force causes the substance between the plates to undergo shear flow with a velocity gradient \(du/dz\). The applied force is proportional to the area and velocity gradient in the fluid:

\[F = \mu A \dfrac{du}{dz},\]

where coefficient \(\mu\) is the dynamic viscosity.

This equation can be expressed in terms of shear stress, \(\tau = F/A\). Thus expressed in differential form for straight, parallel, and uniform flow, the shear stress between layers is proportional to the velocity gradient in the direction perpendicular to the layers:

\[\tau = \mu \dfrac{du}{dz}.\]

Some typical values of \(\mu\) in regular conditions are: \(0.26 [N \cdot s/m^2]\) for oil; \(0.001 [N \cdot s/m^2]\) for water; and \(0.000018 [N \cdot s/m^2]\) for air.

Boundary layer

If one observes the flow around an airfoil, it will be seen that fluid particles in contact with the airfoil have null relative velocity. However, the velocity of the particles at a (relatively low) distance is approximately the velocity of the exterior stream. This thin layer, in which the velocity perpendicular to the airfoil varies dramatically, is known as boundary layer and plays a very important role.

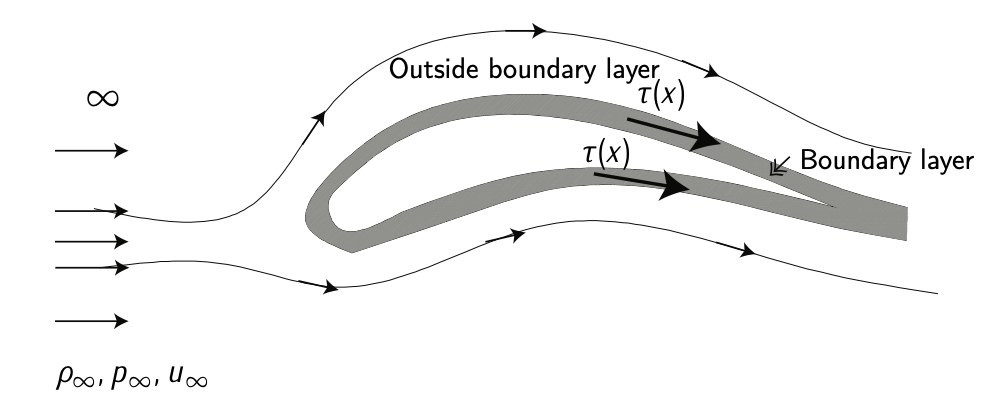
Figure 3.6: Airfoil with boundary layer. The boundary layer has been overemphasized for clarity. Adapted from Franchini et al. [4].

The aerodynamic boundary layer was first defined by Ludwig Prandtl in 1904 Prandtl [5]. It allows to simplify the equations of fluid flow by dividing the flow field into two areas: one inside the boundary layer, where viscosity is dominant and the majority of the drag experienced by a body immersed in a fluid is created, and one outside the boundary layer where viscosity can be neglected without significant effects on the solution. This allows a closed-form solution for the flow in both areas, which is a significant simplification over the solution of the full Navier-Stokes equations. The majority of the heat transfer to and from a body also takes place within the boundary layer, again allowing the equations to be simplified in the flow field outside the boundary layer.

In high-performance designs, such as commercial transport aircraft, much attention is paid to controlling the behavior of the boundary layer to minimize drag. Two effects have to be considered. First, the boundary layer adds to the effective thickness of the body through the displacement thickness, hence increasing the pressure drag. Secondly, the shear forces at the surface of the wing create skin friction drag.

Reynolds number

The dimensionless Reynolds number is due to the studies of Professor Osborne Reynolds (1842-1912) about the conditions in which the flow of fluid in pipes transitioned from laminar flow to turbulent flow. Reynolds used a fluid made of a mixture of water and glycerin, so that varying the mixture the viscosity of the fluid could be modified. When the proportion of glycerin was high, the flow was smooth; by injecting a thread of ink in a pipe with the fluid the thread of ink was flowing smoothly. When the proportion of water was high, by injecting the ink in the pipe a spinning movement was noticed (vortexes) and soon the ink was blurred into the fluid. Reynolds called laminar flow the smooth flow and turbulent flow the chaotic one. He also proved that the character of the flow depended on an dimensionless parameter:

\[\text{Re} = \rho V D/\mu,\]

where \(V\) is the mean velocity of the fluid and \(D\) is the diameter of the pipe. Posterior research named this number the Reynolds number.

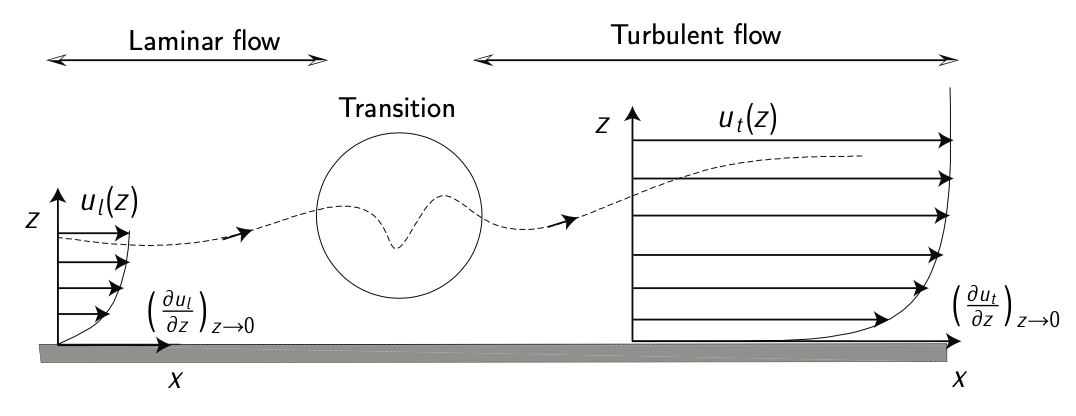
Figure 3.7: Boundary layer transition. Adapted from \(F_{\text{RANCHINI}}\) et al. [4].

More precisely, the Reynolds number \(\text{Re}\) is a dimensionless number that gives a measure of the ratio of inertial forces to viscous forces and consequently quantifies the relative importance of these two types of forces for given flow conditions:

\[\text{Re} = \dfrac{\rho V^2 D^2}{\mu VD}.\]

Laminar flow occurs at low Reynolds numbers, where viscous forces are dominant, and is characterized by smooth, constant fluid motion; turbulent flow occurs at high Reynolds numbers and is dominated by inertial forces, which tend to produce chaotic eddies, vortices, and other flow instabilities.

In the movement of air around the wing, instead of \(D\) it is used the chord of the airfoil, \(c\), the most adequate characteristic longitude. In flight, the Reynolds number is high, of an order of millions, which means the viscosity effects are low and the boundary layer is thin. In this case, the Euler Equation (3.1.3.3) can be used to determine the exterior flow around the airfoil. However, the boundary layer can thicken and the boundary layer drops off along the body, resulting in turbulent flow which increases drag.

Therefore, at high Reynolds numbers, such as typical full-sized aircraft, it is desirable to have a laminar boundary layer. This results in a lower skin friction due to the characteristic velocity profile of laminar flow. However, the boundary layer inevitably thickens and becomes less stable as the flow drops off along the body, and eventually becomes turbulent, the process known as boundary layer transition. One way of dealing with this problem is to suck the boundary layer away through a porous surface (Boundary layer suction). This can result in a reduction in drag, but is usually impractical due to the mechanical complexity involved and the power required to move the air and dispose of it. Natural laminar flow is the name for techniques pushing the boundary layer transition aft by shaping of an airfoil or a fuselage so that their thickest point is aft and less thick. This reduces the velocities in the leading part and the same Reynolds number is achieved with a greater length.