7.1.10: Payload-range diagram
- Page ID
- 78156
Weights of the aircraft
Let us start defining the different weights of the aircraft:
-
\(OEW\): The Operating Empty Weight is the basic weight of an aircraft including the crew, all fluids necessary for operation such as engine oil, engine coolant, water, unusable fuel and all operator items and equipment required for flight but excluding usable fuel and the payload. Also included are certain standard items, personnel, equipment, and supplies necessary for full operation.
-
\(PL\): The Payload is the load for what the company charges a fee. In transportation aircraft it corresponds to the passenger and its luggage, together with the cargo.
-
\(FW\): The Fuel Weight of an aircraft is the total weight of fuel carried at take off and it is calculated adding the following two weights:
1. \(TF\): Trip Fuel is the total amount of fuel estimated to be consumed in the trip.
2. \(RF\): Reserve Fuel is the weight of fuel to allow for unforeseen circumstances, such as an inaccurate weather forecast, alternative arrival airports, etc. -
\(TOW\): The TakeOff weight of an aircraft is the weight at which the aircraft takes off. \(TOW = OEW + PL + FW\).
-
\(LW\): The Landing Weight of an airplane is the total weight of the airplane at destination with no use of reserve fuel. \(LW = OEW + PL + RF\).
-
\(ZFW\): the Zero Fuel Weight of an airplane is the total weight of the airplane and all its contents, minus the total weight of the fuel on board. \(ZFW = OEW + PL\).
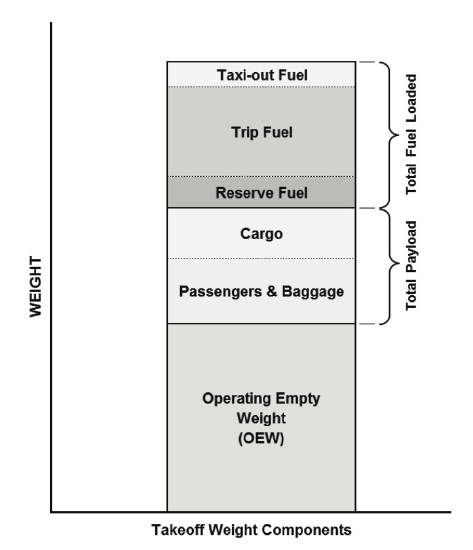
Figure 7.8: Take-off weight components. © Mohsen Alshayef / Wikimedia Commons / CC-BY-SA-3.0.
Limitation on the weight of an aircraft
Due to different features, such structural limits, capacity of tanks, or capacity of passengers and cargo, some of the weights have limitations:
- \(MPL\): The Maximum PayLoad of an aircraft is limited due to structural limits and capacity constraints.
- \(MFW\): The Maximum Fuel Weight is the maximum weight of fuel to be carried and it is limited by the capacity of tanks.
- \(MZFW\): The Maximum Zero Fuel Weight is the maximum weight allowed before usable fuel and other specified usable agents (engine injection fluid, and other consumable propulsion agents) must be loaded in defined sections of the aircraft as limited by strength and airworthiness requirements. It may include usable fuel in specified tanks when carried instead of payload. The addition of usable and consumable items to the zero fuel weight must be in accordance with the applicable government regulations so that airplane structure and airworthiness requirements are not exceeded.
- \(MTOW\): The Maximum Takeoff Weight of an aircraft is the maximum weight at which the pilot of the aircraft is allowed to attempt to take off due to structural or other limits.
- \(MLW\): The Maximum Landing Weight of an aircraft is the maximum weight at which the pilot of the aircraft is allowed to attempt to land due to structural or other limits. In particular, due to structural limits in the landing gear.
Payload-range diagram
A payload range diagram (also known as the elbow chart) illustrates the trade-off between payload and range. The top horizontal line represents the maximum payload. It is limited structurally by maximum zero fuel weight (\(MZFW\)) of the aircraft. Maximum payload is the difference between maximum zero-fuel Weight and operational empty weight (\(OEW\)). Moving left-to-right along the line shows the constant maximum payload as the range increases. More fuel needs to be added for more range.
Weight in the fuel tanks in the wings does not contribute as significantly to the bending moment in the wing as does weight in the fuselage. So even when the airplane has been loaded with its maximum payload that the wings can support, it can still carry a significant amount of fuel.
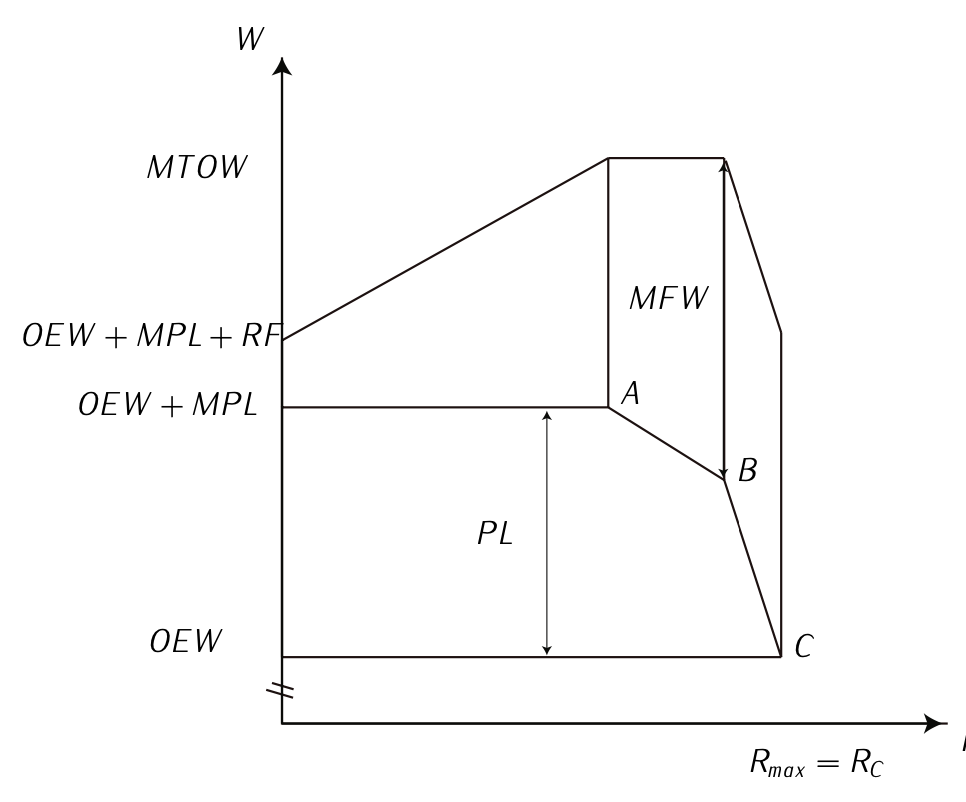
Figure 7.9: Payload-range diagram.
The vertical line represents the range at which the combined weight of the aircraft, maximum payload and needed fuel reaches the maximum take-off weight (\(MTOW\)) of the aircraft. See point A in Figure 7.9. If the range is increased beyond that point, payload has to be sacrificed for fuel.
The maximum take-off weight is limited by a combination of the maximum net power of the engines and the lift/drag ratio of the wings. The diagonal line after the range-at- maximum-payload point shows how reducing the payload allows increasing the fuel (and range) when taking off with the maximum take-off weight. See point B in Figure 7.9.
The second kink in the curve represents the point at which the maximum fuel capacity is reached. Flying further than that point means that the payload has to be reduced further, for an even lesser increase in range. See point C in Figure 7.9. The absolute range is thus the range at which an aircraft can fly with maximum possible fuel without carrying any payload.
In order to relate the ranges with weights we can use to so-called Breguet equation:
\[R = \dfrac{1}{g\eta_j} VE \ln \dfrac{TOW}{LW},\]
For the three marked points, respecitvely \(A\), \(B\) and \(C\):
\[R_A = \dfrac{1}{g\eta_j} VE \ln \dfrac{MTOW}{OEW + MPL + RF},\]
\[R_B = \dfrac{1}{g\eta_j} VE \ln \dfrac{MTOW}{MTOW - MFW + RF},\]
\[R_C = \dfrac{1}{g\eta_j} VE \ln \dfrac{OEW + MFW}{OEW + RF},\]


