7.2.4: Longitudinal stability and control

Last updated
Save as PDF

Page ID: 78161

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Longitudinal static stability

Consider an aircraft in horizontal, steady, linear flight. The aircraft is in equilibrium under equations (7.2.3.3)-(7..2.3.4).

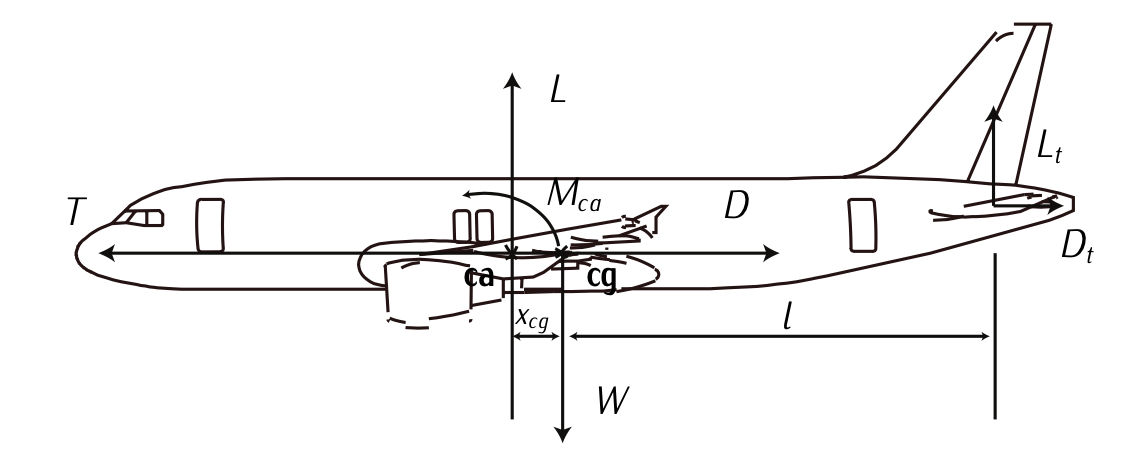
截屏2022-02-07 下午10.10.58.png
Figure 7.13: Longitudinal equilibrium. Adapted from Franchini and García [3].

Consider now that such equilibrium is perturbed by a vertical wind gust, so that the angle of attack increases, that is, there is a perturbation in the angle of attack. In this case, both \(L\) and \(L_t\) increase according to the lift-angle of attack curves (we assume that the behavior for the horizontal stabilizer is similar to the one for the wing⁷) so that we have \(L + \Delta L\) and \(L_t + \Delta L_t\). If \(\Delta L_t l > \Delta L\), then the angle of attack tends to decrease and the aircraft is statically stable. On the contrary, the aircraft is statically unstable. In other words, the torque generated by the horizontal stabilizer is stabilizer (so the name). Obviously, this also depends on the relative position of the aerodynamic centers with respect to the center of gravity of the aircraft8. Therefore, the aerodynamic design is also key to determine the static stability.

The external longitudinal moments acting on the center of gravity can be made dimensionless as follows:

\[\dfrac{\sum M_{cg, y}}{\tfrac{1}{2} \rho SV_{\infty}^2 \bar{c}} = c_{M, cg},\]

where \(\sum M_{cg, y} = -M_{ca} + Lx_{cg} - L_t l\) and \(\bar{c}\) is the mean chord of the aircraft. The dimensionless equation is:

\[c_{M, cg} = c_{M0} + c_{M\alpha} \alpha + c_{M \delta_e} \delta_e,\label{eq7.2.4.2}\]

where \(c_{M, cg}\) is the coefficient of moments of the aircraft with respect to its center of gravity, \(c_{M0}\) is the coefficient of moments independently of the angle of attack and the deflection of the elevator, \(c_{M\alpha}\) is the derivative of the coefficient of moments of the aircraft with respect to the angle of attack, and \(c_{M\delta_e}\) is the derivative of the coefficient of moments of the aircraft with respect to the deflection of the elevator. The coefficients of Equation (\(\ref{eq7.2.4.2}\)) \(c_{M0}\), \(c_{M\alpha}\), and \(c_{M\delta}\) depend on the geometry and the aerodynamics of the aircraft.

截屏2022-02-08 下午8.38.59.png
Figure 7.14: Longitudinal stability. Adapted from Franchini and García [3].

In Figure 7.14 the coefficient of moments of two aircraft as a function of the angle of attack is shown for a given center of gravity, a given aerodynamic center for wing and horizontal stabilizer, and a given deflection of the elevator. The intersection of the curves with the abscissa axis determine the angle of attack of equilibrium \(\alpha_e\). Imagine that a perturbation appears, for instance a wind gust which decreases the angle of attack so that both aircrafts have an angle of attack \(\alpha_1 < \alpha_e\). In the case or aircraft (a), the \(c_{M,cg,b} > 0\) (the curve for \(\alpha_1\) is above the abscissa axis), which means the moment tends to pitch up the aircraft so that it returns to the initial state of equilibrium: the aircraft is statically stable. In the case or aircraft (b), \(c_{M,cg,b} < 0\) (the curve for \(\alpha_1\) is below the abscissa axis) and the moment tends to pitch down the aircraft, so that it is statically unstable.

From this reasoning, we can conclude that for an aircraft to be statically stable it must be fulfilled:

\[\dfrac{dc_{M,cg}}{d\alpha} = c_{M\alpha} < 0.\]

\(c_{M\alpha}\) depends, among other, of the center of gravity of the aircraft. Therefore, one of the key issues in the design of an aircraft is to determine the center of gravity to make the aircraft statically stable. This is not trivial, since the center of gravity varies during the flight (depends on the payload, varies as the fuel is burnt, etc.). Therefore, during a flight the pilot (or the autopilot in control systems) must modify the angle of attack to maintain the flight in the equilibrium (since \(\alpha_e\) varies). As the center of gravity makes its way aft the angle of attack of equilibrium increases. There is a point for which \(c_{M\alpha} = 0\), the neutral point. The center of gravity can not go back beyond this point by any means because \(c_{M\alpha} > 0\) and the aircraft becomes statically unstable.

Longitudinal control

The coefficient \(c_{M\delta_e}\) is referred to as the power of the longitudinal control and represents a measure of the capacity that the elevator has to generate a moment and, therefore, to change the angle of attack at which the aircraft can fly in equilibrium (\(\alpha_e\)).

An elevator's positive deflection \((\delta_e > 0)\) generates an increase in the horizontal stabilizer's lift (\(\Delta L_t\)), which gives rise to a negative pitch moment \(M_{cg} < 0\) (\(c_{M\delta_e} < 0\)). In the condition of equilibrium, the sum of moments around the center of gravity is null, and therefore it must be fulfilled that

\[c_{M, cg} = c_{M0} + c_{M\alpha} \alpha + c_{M\delta_e} \delta_e = 0.\]

Two main problems can be derived in the longitudinal control:

Determine the deflection angle of the elevator, \(\delta_e\), to be able to fly in equilibrium at a given angle of attack, \(\alpha_e\):
\[\delta_e = \dfrac{-c_{M0} - c_{M\alpha} \alpha_e}{c_{M\delta_e}}\]
Determine the angle of attack to fly in equilibrium, \(\alpha_e\), for a known deflection of the elevator, \(\alpha_e\):
\[\alpha_e = \dfrac{-c_{M0} - c_{M\delta_e} \delta_e}{c_{M\alpha}}\]

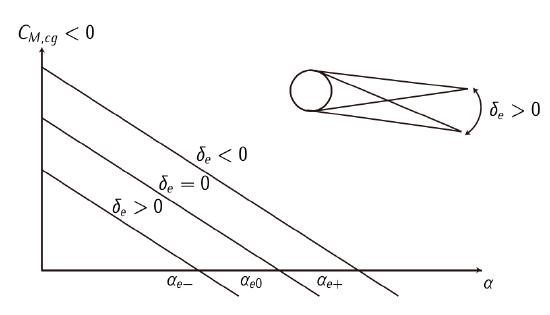
截屏2022-02-08 下午8.53.27.png
Figure 7.15: Effects of elevator on moments coefficient. Adapted from Franchini and García [3].

Figure 7.15 shows the effects of the elevator’s deflection in the angle of attack of equilibrium. Simplifying, for a \(\delta_e < 0\), the angle of attack of equilibrium at which the aircraft flies increases and so does the coefficient of lift. Since the lift must be equal to weight, the aircraft must fly slower. In other words, the elevator is used to modify the velocity of a steady horizontal flight.

As we have pointed out before, the geometric condition of the aircraft vary during the flight. Therefore it is necessary to re-calculate this conditions and modify the variables continuously. This is made using control systems.

7. To be more precise, it is necessary to derive a model which gives us the effective angle of attack of the stabilizer since the wing modifies the incident current. However, this will be studied in posterior courses.

8. remember that the aerodynamic center is the point at with the pitching moment does not vary with respect the increase in \(C_L\).