12.2: Orientation between reference frames
- Page ID
- 77997
According to the classical mechanics, to orientate without loss of generality a reference frame system \(F_I\) with respect to another \(F_F\): if both have common origin, it is necessary to perform a generic rotation until axis coincide; if the origin differs, it is necessary, together with the mentioned rotation, a translation to make origins coincide.
There are different methods to orientate two systems with common origin, such for instance, directors cosinos, quaternions or the Euler angles, which indeed will be used in this dissertation.
Euler angles represent three composed and finite rotations given in a pre-establish order that move a reference frame to a given referred frame. This is equivalent to saying that any orientation can be achieved by composing three elemental and finite rotations (rotations around a single axis of a basis), and also equivalent to saying that any rotation matrix can be decomposed as a product of three elemental rotation matrices.
The pre-establish order of elemental rotations is usually referred to as Convention. In aeronautics and space vehicles it is universally utilized the Tailt-Bryan Convention. Such convention is also referred to as Convention 321.
If the three components of a vector \(\vec{A}\) in \(F_I\) are known, the transformation or rotation matrixx \(L_{F_I}\) expresses a vector \(\vec{A}\) in the reference system \(F_F\) as follows:
\[\vec{A}_F = L_{F_I} \vec{A}_I\]
\(L_{F_I}\) can be obtained by simply obtaining the three individual rotation matrixes and properly multiplying them.
Given two reference systems, \(F_I\) and \(F_F\), with common origin, we want to make \(F_I\) coincide with \(F_F\): first we rotate \(F_I\) around axis \(z_I\) an angle \(\delta_3\), obtaining the first intermediate reference systems \(F_1\). Second, we rotate system \(F_1\) around axis \(y_1\) an angle \(\delta_2\), obtaining the second intermediate reference system \(F_2\). Third, we rotate the system \(F_2\) around axis \(x_2\) an angle \(\delta_1\), obtaining the final reference system \(F_F\).
First, we express the unit vector of \(F_1\) as a function of unit vector of \(F_I\):
\[\begin{bmatrix} \vec{i}_1 \\ \vec{j}_1 \\ \vec{k}_1 \end{bmatrix} = \begin{bmatrix} \cos \delta_3 & \sin \delta_3 & 0 \\ -\sin \delta_3 & \cos \delta_3 & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} \vec{i}_I \\ \vec{j}_I \\ \vec{k}_I \end{bmatrix}\]
The rotation matrix will be:
\[L_{1I} = R_3 (\delta_3) = \begin{bmatrix} \cos \delta_3 & \sin \delta_3 & 0 \\ -\sin \delta_3 & \cos \delta_3 & 0 \\ 0 & 0 & 1 \end{bmatrix}.\]
where \(R_3 (\delta_3)\) is the notation of the individual matrix of rotation of an angle \(\delta_3\) around the third axis (axis \(z\)).
Therefore, the vector \(\vec{A}\) expressed in the first intermediate reference frame \(F_1\) (Notated \(\vec{A}_1\)) will be:
\[\vec{A}_1 = L_{1I} \vec{A}_I.\]
Operating analogously for the second individual rotation:
\[\begin{bmatrix} \vec{i}_1 \\ \vec{j}_1 \\ \vec{k}_1 \end{bmatrix} = \begin{bmatrix} \cos \delta_2 & 0 & -\sin \delta_2 \\ 0 & 1 & 0 \\ \sin \delta_2 & 0 & \cos \delta_2 \end{bmatrix} \begin{bmatrix} \vec{i}_1 \\ \vec{j}_1 \\ \vec{k}_1 \end{bmatrix}\]
\[L_{21} = R_2 (\delta_2) = \begin{bmatrix} \cos \delta_2 & 0 & -\sin \delta_2 \\ 0 & 1 & 0 \\ \sin \delta_2 & 0 & \cos \delta_2 \end{bmatrix}\]
\[\vec{A}_2 = L_{21} \vec{A}_1.\]
Finally, for the third individual rotation:
\[\begin{bmatrix} \vec{i}_F \\ \vec{j}_F \\ \vec{k}_F \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos \delta_1 & \sin \delta_1 \\ 0 & -\sin \delta_1 & \cos \delta_1 \end{bmatrix} \begin{bmatrix} \vec{i}_2 \\ \vec{j}_2 \\ \vec{k}_2 \end{bmatrix}\]
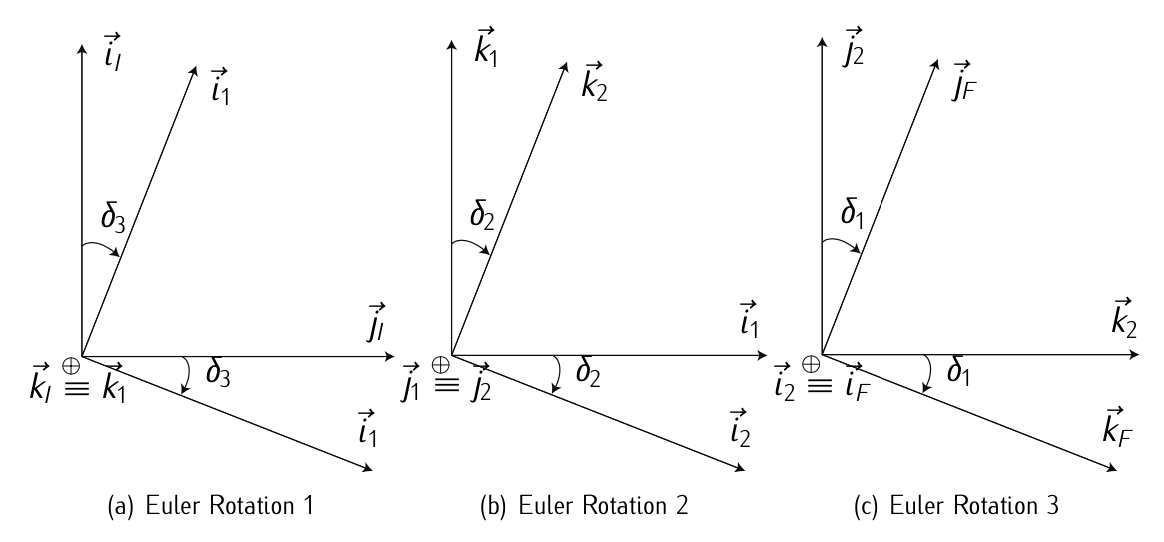
Figure 12.1: Fuler angles
\[L_{F2} = R_1 (\delta_1) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos \delta_1 & \sin \delta_1 \\ 0 & -\sin \delta_1 & \cos \delta_1 \end{bmatrix}\]
\[\vec{A}_F = L_{F2} \vec{A}_2.\]
Composing:
\[\vec{A}_F = L_{F2} L_{21} L_{1I} \vec{A}_I,\]
and the global rotation matrix will be:
\[L_{FI} = \begin{bmatrix} \cos \delta_2 \cos \delta_3 & \cos \delta_2 \sin \delta_3 & -\sin \delta_2 \\ \sin \delta_1 \sin \delta_2 \cos \delta_3 - \cos \delta_1 \sin \delta_3 & \sin \delta_1 \sin \delta_2 \sin \delta_3 + \cos \delta_1 \cos \delta_3 & \sin \delta_1 \cos \delta_2 \\ \cos \delta_1 \sin \delta_2 \cos \delta_3 + \sin \delta_1 \sin \delta_3 & \cos \delta_1 \sin \delta_2 \sin \delta_3 - \sin \delta_1 \cos \delta_3 & \cos \delta_1 \cos \delta_2 \end{bmatrix}\]


