13.2.4: Proposed solution

Last updated
Save as PDF

Page ID: 78428

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Hereby, an schematic solution for the aircraft trajectory is proposed. Notice that, for the sake of conciseness, only the climb phase is presented. Both Cruise and descent phases are left as exercises to the students:

An Airbus A320 is selected. A Python based code (A320.py), including A320 BADA parameter values, is provided along the text.
A Python based code (file ODE_Aircraft.py), including values and description of the different steps, is also provided.
A 4th order Runge-Kutta method is used to solve the set of differential equations. Notice that numerical methods are out of the scope of this course; they are to be studied within a numerical calculus course.

截屏2022-03-15 下午8.37.06.png
Figure 13.4: Aircraft climb motion solution.

The evolution mass, true airspeed, altitude, and flight path angle, is presented in Figure 13.4. Notice that the oscillations in Flight Path Angle and True airspeed are natural with open-loop, fixed controls (as it is our case): they correspond to the activation of the so-called phugoid mode. Real aircraft include close-loop control systems that counteract this oscillating behaviour. Aircraft engine modes and aircraft response to both open-loop and close loop control are out of the scope of this course. They should be studied in advanced courses of mechanics of flight and aircraft dynamic stability and control.

A320.py data file

截屏2022-03-15 下午8.38.19.png

Main file ODE_Aircraft.py

截屏2022-03-15 下午8.42.23.png
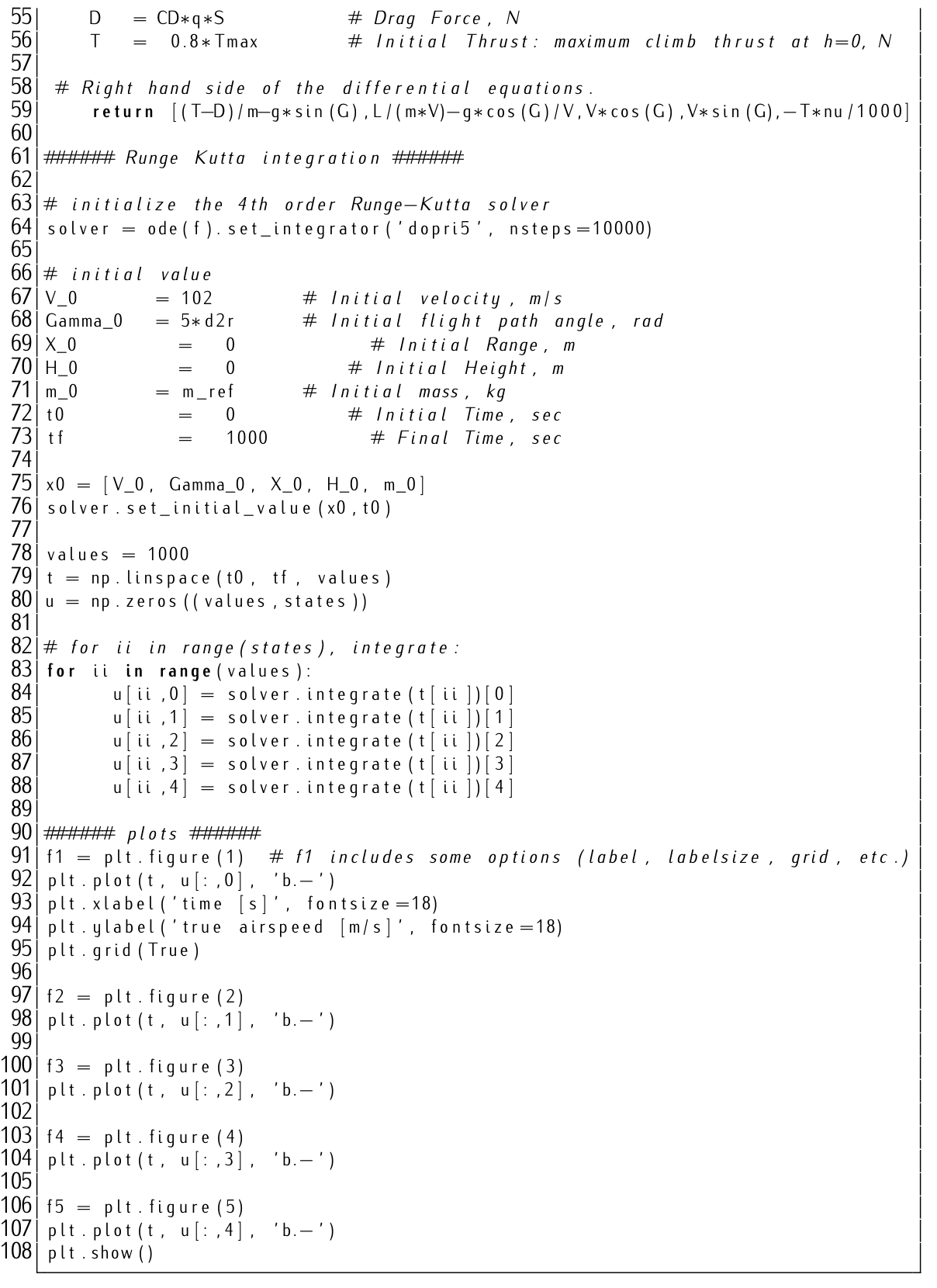
截屏2022-03-15 下午8.44.06.png

Figure 13.4 presents the solution obtained after running the given code in Python. Notice that this solution corresponds only to the climb phase. Recall what was mentioned before on the oscillations.

Students are challenged to complete the exercise by integrating a cruise phase and then a descent phase. Students are also challenged to solve the problem in a more operational manner, that is, instead of ascending at constant Thrust and optimum coefficient of lift, something that aircraft do not do in real operation, one could set two constraints to close up the degrees of freedom of the problem:

ascent at a rate of climb of 2000 ft/min;
follow a constant CAS procedure (say 250 kts), reach the transition Mach (say M = 0.78), and then a constant Mach.

The student should observe how oscillations disappear.