2.2: Visible and Near Infrared Optical Spectroscopic Sensors for Biosystems Engineering
- Page ID
- 46843
Nathalie Gorretta
University of Montpellier, INRAe and SupAgro
Montpellier, France
Aoife A. Gowen
UCD School of Biosystems and Food Engineering
University College Dublin, Ireland
Variables
Introduction
Optical sensors are a broad class of devices for detecting light intensity. This can be a simple component for notifying when ambient light intensity rises above or falls below a prescribed level, or a highly sensitive device with the capacity to detect and quantify various properties of light such as intensity, frequency, wavelength, or polarization. Among these sensors, optical spectroscopic sensors, where light interaction with a sample is measured at many different wavelengths, are popular tools for the characterization of biological resources, since they facilitate comprehensive, non-invasive, and non-destructive monitoring. Optical sensors are widely used in the control and characterization of various biological environments, including food processing, agriculture, organic waste sorting, and digestate control.
The theory of spectroscopy began in the 17th century. In 1666, Isaac Newton demonstrated that white light from the sun could be dispersed into a continuous series of colors (Thomas, 1991), coining the word spectrum to describe this phenomenon. Many other researchers then contributed to the development of this technique by showing, for example, that the sun’s radiation was not limited to the visible portion of the electromagnetic spectrum. William Herschel (1800) and Johann Wilhelm Ritter (1801) showed that the sun’s radiation extended into the infrared and ultraviolet, respectively. A major contribution by Joseph Fraunhofer in 1814 laid the foundations for quantitative spectrometry. He extended Newton’s discovery by observing that the sun’s spectrum was crossed by a large number of fine dark lines now known as Fraunhofer lines. He also developed an essential element of future spectrum measurement tools (spectrometers) known as the diffraction grating, an array of slits that disperses light. Despite these major advances, Fraunhofer could not give an explanation as to the origin of the spectral lines he had observed. It was only later, in the 1850s, that Gustav Kirchoff and Robert Bunsen showed that each atom and molecule has its own characteristic spectrum. Their achievements established spectroscopy as a scientific tool for probing atomic and molecular structure (Thomas, 1991; Bursey, 2017).
Many terms are used to describe the measurement of electromagnetic energy at different wavelengths, such as spectroscopy, spectrometry, and spectrophotometry. The word spectroscopy originates from the combination of spectro (from the Latin word specere, meaning “to look at”) with scopy (from the Greek word skopia, meaning “to see”). Following the achievements of Newton, the term spectroscopy was first applied to describe the study of visible light dispersed by a prism as a function of its wavelength. The concept of spectroscopy was extended, during a lecture by Arthur Schuster in 1881 at the Royal Institution, to incorporate any interaction with radiative energy according to its wavelength or frequency (Schuster, 1911). Spectroscopy, then, can be summarized as the scientific study of the electromagnetic radiation emitted, absorbed, reflected, or scattered by atoms or molecules. Spectrometry or spectrophotometry is the quantitative measurement of the electromagnetic energy emitted, reflected, absorbed, or scattered by a material as a function of wavelength. The suffix “-photo” (originating from the Greek term phôs, meaning “light”) refers to visual observation, for example, printing on photographic film, projection on a screen, or the use of an observation scope, while the suffix “-metry” (from the Greek term metria, meaning the process of measuring) refers to the recording of a signal by a device (plotter or electronic recording).
Spectroscopic data are typically represented by a spectrum, a plot of the response of interest (e.g. reflectance, transmittance) as a function of wavelength or frequency. The instrument used to obtain a spectrum is called a spectrometer or a spectrophotometer. The spectrum, representing the interaction of electromagnetic radiation with matter, can be analyzed to gain information on the identity, structure, and energy levels of atoms and molecules in a sample.
Two major types of spectroscopy have been defined, atomic and molecular. Atomic spectroscopy refers to the study of electromagnetic radiation absorbed or emitted by atoms, whereas molecular spectroscopy refers to the study of the light absorbed or emitted by molecules. Molecular spectroscopy provides information about chemical functions and structure of matter while atomic spectroscopy gives information about elemental composition of a sample. This chapter focuses on molecular spectroscopy, particularly in the visible-near infrared wavelength region due to its relevance in biosystems engineering.
Concepts
Light and Matter Interaction
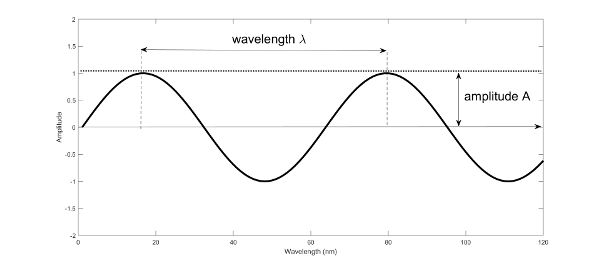
Spectroscopy is based on the way electromagnetic energy interacts with matter. All light is classified as electromagnetic radiation consisting of alternating electric and magnetic fields and is described classically by a continuous sinusoidal wave-like motion of the electric and magnetic fields propagating transversally in space and time. Wave motion can be described by its wavelength \(\lambda\) (nm), the distance between successive maxima or minima, or by its frequency ν (Hz), the number of oscillations of the field per second (Figure 2.2.1). Wavelength is related to the frequency via the speed of light c (3 × 108 m s−1) according to the relationship given in Equation 2.2.1.
\[ \lambda = \frac{c}{v} \]
Sometimes it is convenient to describe light in terms of units called “wavenumbers,” where the wavenumber is the number of waves in one centimeter. Thus, wavenumbers are frequently used to characterize infrared radiation. The wavenumber, \(\bar{\nu}\) is formally defined as the inverse of the wavelength, \(\lambda\) expressed in centimeters:
\[ \bar{\nu}=\frac{1}{\lambda} \]
The wavenumber is therefore directly proportional to frequency, ν:
\[ v = c\bar{\nu} \]
leading to the following conversion relationships:
\[ \bar{\nu} (\text{cm}^{-1}) = \frac{10^{7}}{\lambda{\text{(nm)}}} \]
\[ \lambda{\text{(nm)} = \frac{10^{7}}{\bar{\nu}(\text{cm}^{-1})}} \]
The propagation of light is described by the theory of electromagnetic waves proposed by Christian Huygens in 1878 (Huygens, 1912). However, the interaction of light with matter (emission or absorption) also leads to the particle nature of light and electromagnetic waves as proposed by Planck and Einstein in the early 1900s. In this theory, light is considered to consist of particles called photons, moving at the speed c. Photons are “packets” of elementary energy, or quanta, that are exchanged during the absorption or emission of light by matter.
| Wavelength \(\lambda\) |
Wavenumber \(\bar{\nu}\) |
Relation | |
|---|---|---|---|
|
Unit |
cm |
cm−1 |
\(\bar{\nu}= \frac{1}{\lambda}\) |
|
nm |
cm−1 |
\(\bar{\nu}= \frac{10^{7}}{\lambda}\) |
The energy of photons of light is directly proportional to its frequency, as described by the fundamental Planck relation (Equation 2.2.6). Thus, high energy radiation (such as X-rays) has high frequencies and short wavelengths and, inversely, low energy radiation (such as radio waves) has low frequencies and long wavelengths.
\[ E =h\nu=\frac{hc}{\lambda}=hc\bar{\nu} \]
where E = energy of photons of light (J)
h = Plank’s constant = 6.62607004 × 10−34 J·s
ν = frequency (Hz)
c = speed of light (3 ×108 m s−1)
\(\lambda\) = wavelength (m)
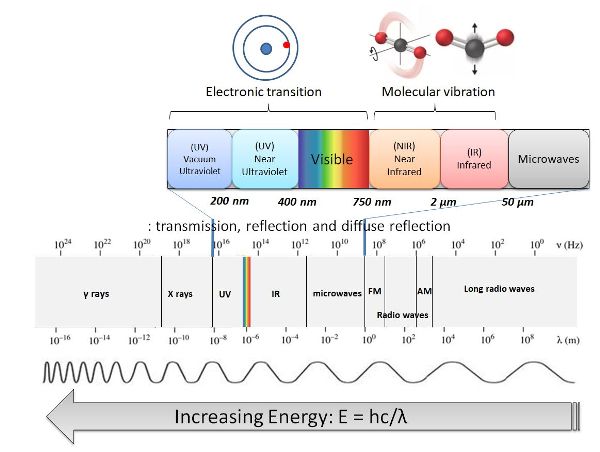
The electromagnetic spectrum is the division of electromagnetic radiation according to its different components in terms of frequency, photon energy or associated wavelengths, as shown in Figure 2.2.2. The highest energy radiation corresponds to the γ-ray region of the spectrum. At the other end of the electromagnetic spectrum, radio frequencies have very low energy (Pavia et al., 2008). The visible region only makes up a small part of the electromagnetic spectrum and ranges from 400 to about 750 nm. The infrared (IR) spectral region is adjacent to the visible spectral region and extends from about 750 nm to about 5 × 106 nm. It can be further subdivided into the near-infrared region (NIR) from about 750 nm to 2,500 nm which contains the short wave-infrared (SWIR) from 1100–2500 nm, the mid-infrared (MIR) region from 2,500 nm to 5 × 104 nm, and the far-infrared (FIR) region from 5 × 104 nm to 5 × 106 nm (Osborne et al., 1993).
When electromagnetic radiation collides with a molecule, the molecule’s electronic configuration is modified. This modification is related to the wavelength of the radiation and consequently to its energy. The interaction of a wave with matter, whatever its energy, is governed by the Bohr atomic model and derivative laws established by Bohr, Einstein, Planck, and De Broglie (Bohr, 1913; De Broguie, 1925). Atoms and molecules can only exist in certain quantified energy states. The energy exchanges between matter and radiation can, therefore, only be done by specific amounts of energy or quanta \( \Delta{E} =h\nu \). These energy exchanges can be carried out in three main ways (Figure 2.2.3): absorption, emission, or diffusion.
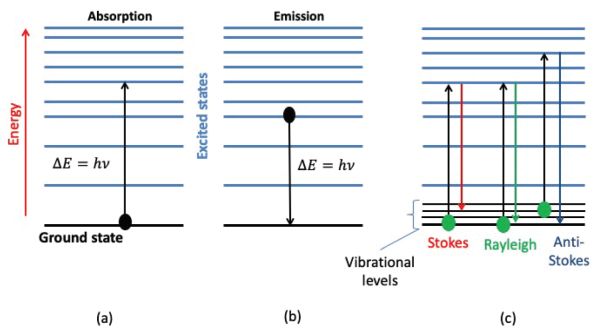
In absorption spectroscopy, a photon is absorbed by a molecule, which undergoes a transition from a lower-energy state Ei to a higher energy or excited state Ej such that Ej – Ei = hν. In emission spectroscopy, a photon can be emitted by a molecule that undergoes a transition from a higher energy state Ej to a lower energy state Ei such that Ej – Ei = hν. In diffusion or scattering spectroscopy, a part of the radiation interacting with matter is scattered in many directions by the particles of the sample. If, after an interaction, the photon energy is not modified, the interaction is known as elastic. This corresponds to Rayleigh or elastic scattering, which maintains the frequency of the incident wave. When the photon takes or gives energy to the matter and undergoes a change in energy, the interaction is called inelastic, corresponding, respectively, to Stokes or anti-Stokes Raman scattering. Transitions between energy states are referred to as absorption or emission lines for absorption and emission spectroscopy, respectively.
Absorption Spectrometry
In absorption spectrometry, transitions between energy states are referred to as absorption lines. These absorption lines are typically classified by the nature of the electronic configuration change induced in the molecule (Sun, 2009):
- • Rotation lines occur when the rotational state of a molecule is changed. They are typically found in the microwave spectral region ranging between 100 μm and 1 cm.
- • Vibrational lines occur when the vibrational state of the molecule is changed. They are typically found in the IR, i.e., in the spectral range between 780 and 25,000 nm. Overtones and combinations of the fundamental vibrations in the IR are found in the NIR range (Figure 2.2.2).
- • Electronic lines correspond to a change in the electronic state of a molecule (transitions of the energetic levels of valence orbitals). They are typically found in the ultraviolet (approx. 200–400 nm) and visible region (approx. 200–400 nm). In the visible region (350–800 nm), molecules such as carotenoids and chlorophylls absorb light due to their molecular structure. This visible spectral range is also used to evaluate color (for instance, of food or vegetation). In the ultraviolet spectral range, fluorescence and phosphorescence can be observed. While fluorescence and phosphorescence are both spontaneous emission of electromagnetic radiation, they differ in the way the excited molecule loses its energy after it has been irradiated. The glow of fluorescence stops right after the source of excitatory radiation is switched off, whereas for phosphorescence, an afterglow can last from fractions of a second to hours.
The spectral ranges selected for measurement and analysis depend on the application and the materials to be characterized. Absorption spectroscopy in the visible and NIR is commonly used for the characterization of biological systems due to the many advantages associated with this wavelength range, including rapidity, non-invasivity, non-destructive measurement, and significant incident wave penetration. Moreover, the NIR range enables probing of molecules containing C-H, N-H, S-H, and O-H bonds, which are of particular interest for characterization of biological samples (Pasquini, 2018; 2003). In addition to the chemical characterization of materials, it is possible to quantify the concentration of certain molecules using the Beer-Lambert law, described in detail below.
Beer-Lambert Law
Incident radiation passing through a medium undergoes several changes, the extent of which depends on the physical and chemical properties of the medium. Typically, part of the incident beam is reflected, another part is absorbed and transformed into heat by interaction with the material, and the rest passes through the medium. Transmittance is defined as the ratio of the transmitted light intensity to the incident light intensity (Equation 2.2.7). Absorbance is defined as the logarithm of the inverse of the transmittance (Equation 2.2.8). Absorbance is a positive value, without units. Due to the inverse relationship between them, absorbance is greater when the transmitted light is low.
\[ T= \frac{I}{I_{0}} \]
\[ A=log(\frac{1}{T})=log(\frac{I_{0}}{I}) \]
where T = transmittance
I = transmitted light intensity
I0 = incident light intensity
A = absorbance (unitless)
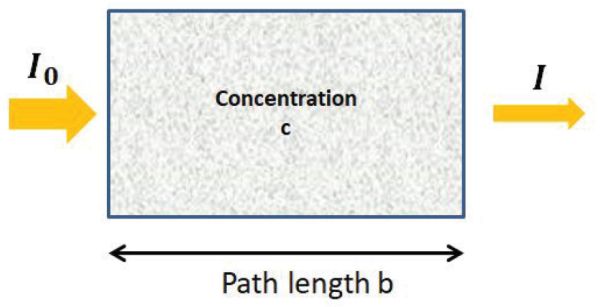
The Beer-Lambert law (Equation 2.2.9) describes the linear relationship between absorbance and concentration of an absorbing species. At a given wavelength λ, absorbance A of a solution is directly proportional to its concentration (C) and to the length of the optical path (b), i.e., the distance over which light passes through the solution (Figure 2.2.4, Equation 2.2.9). When the concentration is expressed in moles per liter (mol L−1), the length of the optical path in centimeters (cm), the molar absorptivity or the molar extinction coefficient ε is expressed in L mol−1 cm−1.
Molar absorptivity is a measure of the probability of the electronic transition and depends on the wavelength but also on the solute responsible for absorption, the temperature and, to a lesser extent, the pressure.
\[ A=\epsilon bC \]
where A = absorbance (unitless)
ε = molar absorptivity or molar extinction coefficient = Beer-Lambert proportionality constant (L mol−1 cm−1)
b = path length of the sample (cm)
C = concentration (mol L−1)
Beer-Lambert Law Limitations
Under certain circumstances, the linear relationship between the absorbance, the concentration, and the path length of light can break down due to chemical and instrumental factors. Causes of nonlinearity include the following:
- • Deviation of absorptivity coefficient: The Beer-Lambert law is capable of describing the behavior of a solution containing a low concentration of an analyte. When analyte concentration is too high (typically >10 mM), electrostatic interactions between molecules close to each other result in deviations in absorptivity coefficients.
- • High analyte concentrations can also alter the refractive index of the solution which in turn could affect the absorbance obtained.
- • Scattering: Particulates in the sample can induce scattering of light.
- • Fluorescence or phosphorescence of the sample.
- • Non-monochromatic radiation due to instrumentation used.
Non-linearity can be detected as deviations from linearity when the absorbance is plotted as a function of concentration (see example 1). This is usually overcome by reducing analyte concentration through sample dilution.
Spectroscopic Measurements
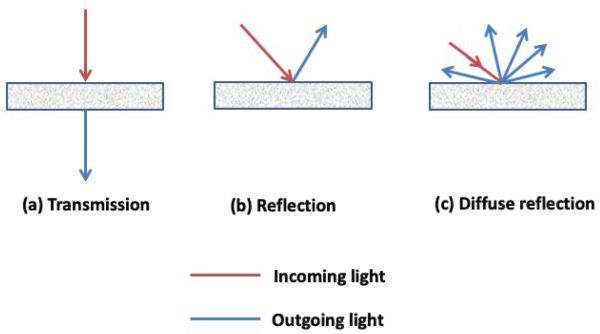
Spectrometers are optical instruments that detect and measure the intensity of light at different wavelengths. Different measurement modes are available, including transmission, reflection, and diffuse reflection (Figure 2.2.5). In transmission mode, the spectrometer captures the light transmitted through a sample, while in reflectance mode, the spectrometer captures the light reflected by the sample. In some situations, e.g., for light-diffusing samples such as powders, reflected light does not come solely from the front surface of the object; radiation that penetrates the material can reappear after scattering of reflection within the sample. These radiations are called diffuse reflection.
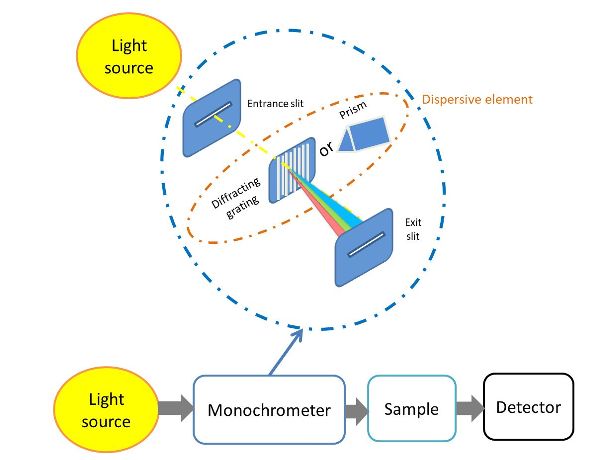
Spectrometers share several common basic components, including a source of light energy, a means for isolating a narrow range of wavelengths (typically a dispersive element), and a detector. The dispersive element must allow light of different wavelengths to be separated (Figure 2.2.6).
The light source is arguably the most important component of any spectrophotometer. The ideal source is a continuous one that contains radiation of uniform intensity over a large range of wavelengths. Other desirable properties are stability over time, long service life, and low cost. Quartz-tungsten halogen lamps are commonly used as light sources for the visible (Vis) and NIR regions, and deuterium lamps or high-powered light emitting diodes may be used for the ultraviolet region.
The light produced by the light source is then focused and directed to the monochromater by an entrance slit. A grating diffraction element is then used to split the white light from the lamp into its components. The distance between the lines on gratings (“grating pitch”) is of the same order of magnitude as the wavelength of the light to be analyzed. The separated wavelengths then propagate towards the sample compartment through the exit slit.
Depending on the technology used for the detector, the sample can be positioned before or after the monochromater. For simplicity, this chapter describes a positioning of the sample after the monochromater; the entire operation described above is valid regardless of the positioning of the sample.
In some spectrometers, an interferometer (e.g. Fabry-Pérot or Fourier-transform interferometer for UV and IR spectral range, respectively) is used instead of a diffraction grating to obtain spectral measurements. In this case, the initial beam light is split into two beams with different optical paths by using mirror arrangements. These two beams are then recombined before arriving at the detector. If the optical path lengths of the two beams do not differ by too much, an interference pattern is produced. A mathematical operation (Fourier transform) is then applied to the obtained interference pattern (interferogram) to produce a spectrum.
Once the light beams have passed through the samples, they will continue to the detector or photodetector. A photodetector absorbs the optical energy and converts it into electrical energy. A photodetector is a multichannel detector and can be a photodiode array, a charge coupled device (CCD), or a complementary metal oxide semiconductor (CMOS) sensor. While photodetectors can be characterized in many different ways, the most important differentiator is the detector material. The two most common semiconductor materials used in Vis-NIR spectrometers are silicon (Si) and indium gallium arsenide (InGaAs).
Spectral Imaging
Spectral imaging is a technique that integrates conventional imaging and spectroscopy to obtain both spatial and spectral information from an object. Multispectral imaging usually refers to spectral images in which <10 spectral bands are collected, while hyperspectral imaging is the term used when >100 contiguous spectral bands are collected. The term spectral imaging is more general. Spectral images can be represented as three-dimensional blocks of data, comprising two spatial and one wavelength dimension.
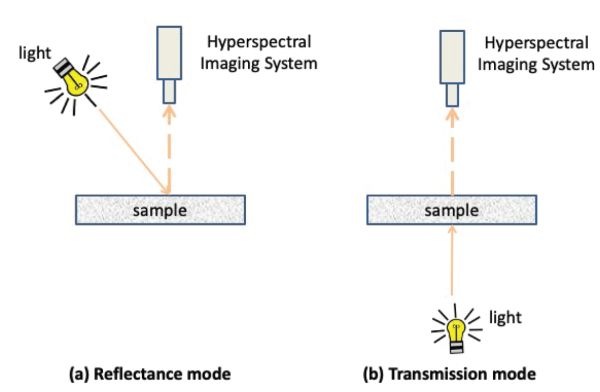
Two sensing modes are commonly used to acquire hyperspectral images, i.e., reflectance and transmission modes (Figure 2.2.7). The use of these modes depends on the objects to be characterized (e.g., transparent or opaque) and the properties to be determined (e.g. size, shape, chemical composition, presence of defects). In reflectance mode, the hyperspectral sensor and light are located on the same side of the object and the imaging system acquires the light reflected by the object. In this mode, the lighting system should be designed to avoid any specular reflection. Specular reflection occurs when a light source can be seen as a direct reflection on the surface of an object. It is characterized by an angle of reflection being equal to the angle of incidence of the incoming light source on the sample. Specular reflection appears as bright saturated spots on acquired images impacting their quality. In transmittance mode, the detector is located in the opposite side of the light source and captures the transmitted light through the sample.
Applications
Vegetation Monitoring in Agriculture
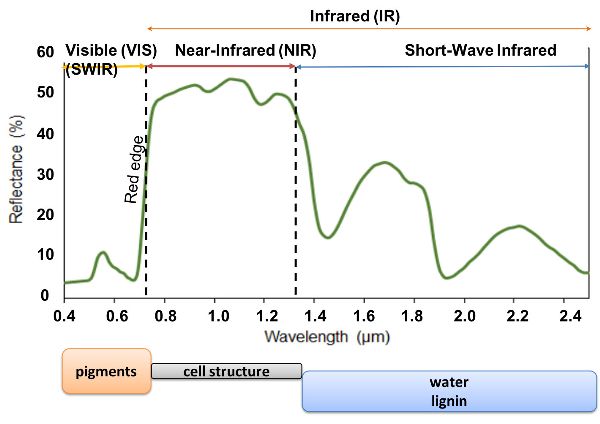
The propagation of light through plant leaves is governed primarily by absorption and scattering interactions and is related to chemical and structural composition of the leaves. Spectral characteristics of radiation reflected, transmitted, or absorbed by leaves can thus provide a more thorough understanding of physiological responses to growth conditions and plant adaptations to the environment. Indeed, the biochemical components and physical structure of vegetation are related to its state of growth and health. For example, foliar pigments including chlorophyll a and b, carotenoids, and anthocyanins are strong absorbers in the Vis region and are abundant in healthy vegetation, causing plant reflectance spectra to be low in the Vis relative to NIR wavelength range (Asner, 1998; Ollinger, 2011) (Figure 2.2.8). Chlorophyll pigments absorb violet-blue and red light for photosynthesis, the process by which plants use sunlight to synthesize organic matter. Green light is not absorbed by photosynthesis and reflectance spectra of green vegetation in the visible range are maximum around 550 nm. This is why healthy leaves appear to be green. The red edge refers to the area of the sudden increase in the reflectance of green vegetation between 670 and 780 nm. The reflectance in the NIR plateau (800–1100 nm) is a region where biochemical absorptions are limited and is affected by the scattering of light within the leaf, the extent of which is related to the leaf’s internal structure. Reflectance in the short wave-IR (1100–2500 nm) is characterized by strong water absorption and minor absorptions of other foliar biochemical contents such as lignin, cellulose, starch, protein, and cellulose.
Stress conditions on plants, such as drought and pathogens, will induce changes in reflectance in the Vis and NIR spectral domain due to degradation of the leaf structure and the change of the chemical composition of certain tissues. Consequently, by measuring crop reflectance in the Vis and NIR regions of the spectrum, spectrometric sensors are able to monitor and estimate crop yield and crop water requirements and to detect biotic or abiotic stresses on vegetation. Vegetation indices (VI), which are combinations of reflectance images at two or more wavelengths designed to highlight a particular property of vegetation, can then be calculated over these images to monitor vegetation changes or properties at different spatial scales.
The normalized difference vegetation index (NDVI) (Rouse et al., 1974) is the ratio of the difference between NIR and red reflectance, divided by the sum of the two:
\[ NDVI = \frac{R_{NIR}-R_{R}}{R_{NIR}+R_{R}} \]
where RNIR = reflectance in the NIR spectral region (one wavelength selected over the 750–870 nm spectral range) and RR = reflectance in the red spectral region (one wavelength selected over 580–650 nm spectral range). Dividing by the sum of the two bands reduces variations in light over the field of view of the image. Thus, NDVI maintains a relatively constant value regardless of the overall illumination, unlike the simple difference which is very sensitive to changes in illumination. NDVI values can range between −1 and +1, with negative values corresponding to surfaces other than plant cover, such as snow or water, for which the red reflectance is higher than that in the NIR. Bare soils, which have red and NIR reflectance about the same order of magnitude, NDVI values are close to 0. Vegetation canopies have positive NDVI values, generally in the range of 0.1 to 0.7, with the highest values corresponding to the densest vegetation coverage.
NDVI can be correlated with many plant properties. It has been, and still is, used to characterize plant health status, identify phenological changes, estimate green biomass and yields, and in many other applications. However, NDVI also has some weaknesses. Atmospheric conditions and thin cloud layers can influence the calculation of NDVI from satellite data. When vegetation cover is low, everything under the canopy influences the reflectance signal that will be recorded. This can be bare soil, plant litter, or other vegetation. Each of these types of ground cover will have its own spectral signature, different from that of the vegetation being studied. Other indices to correct NDVI defects or to estimate other vegetation parameters have been proposed, such as the normalized difference water index or NDWI (Gao, 1996), which uses two wavelengths located respectively in the NIR and the SWIR regions (750–2500 nm) to track changes in plant moisture content and water stress (Eq. 2.2.11). Both wavelengths are located in a high reflectance plateau (Fig. 2.2.8) where the vegetation scattering properties are expected to be about the same. The SWIR reflectance is affected by the water content of the vegetation. The combination of the NIR and the SWIR wavelength is thus not sensitive to the internal structure of the leaf but is affected by vegetation water content. The normalized difference water index is:
\[ NDWI=\frac{R_{NIR}-R_{SWIR}}{R_{NIR}+R_{SWIR}} \]
where RNIR is the reflectance in the NIR spectral region (one wavelength selected over the 750–870 nm spectral range) and RSWIR is the reflectance in the SWIR spectral region around 1240 nm (water absorption band). Gao (1996) proposed using RNIR equal to reflectance at 860 nm and RSWIR at 1240 nm.
Absorption spectroscopy is widely used for monitoring and characterizing vegetation at different spatial, spectral, and temporal scales. Sensors are available mainly for broad-band multispectral or narrow-band hyperspectral data acquisition. Platforms are space-borne for satellite-based sensors, airborne for sensors on manned and unmanned airplanes, and ground-based for field and laboratory-based sensors.
Satellites have been used for remote sensing imagery in agriculture since the early 1970s (Bauer and Cipra, 1973; Doraiswamy et al., 2003) when Landsat 1 (originally known as Earth Resources Technology Satellite 1) was launched. Equipped with a multispectral scanner with four wavelength channels (one green, one red and two IR bands), this satellite was able to acquire multispectral images with 80 m spatial resolution and 18-day revisit time (Mulla 2013). Today, numerous multispectral satellite sensors are available and provide observations useful for assessing vegetation properties far better than Landsat 1. Landsat 8, for example, launched in 2013, offers nine spectral bands in the Vis to short-wave IR spectral range (i.e., 400–2500 nm) with a spatial resolution of 15–30 m and a 16-day revisit time. Sentinel-2A and Sentinel-2B sensors launched in 2015 and 2017, respectively, have 13 spectral bands (400–2500 nm) and offer 10–30 m multi-spectral global coverage and a revisit time of less than 10 days. Hyperspectral sensors, however, are still poorly available on satellites due to their cost and their relatively short operating life. Among them, Hyperion (EO-1 platform) has 220 spectral bands over the 400–2500 nm spectral range, a spatial resolution of 30 m, and a spectral resolution of 10 nm. The next generation, such as PRISMA (PRecursore IperSpettrale della Missione Applicativa) with a 30 m spatial resolution and a wavelength range of 400–2505 nm and the EnMAP (Environmental Mapping and Analysis Program) with a 30 m spatial resolution and a wavelength range of 400–2500 nm (Transon et al., 2018), indicate the future for this technology.
Some companies now use satellite images to provide a service to help farmers manage agricultural plots. Farmstar (www.myfarmstar.com/web/en) and Oenoview (https://www.icv.fr/en/viticulture-oenology-consulting/oenoview), for example, support management of inputs and husbandry in cereal and vine crops, respectively. However, satellite-based sensors often have an inadequate spatial resolution for precision agriculture applications. Some farm management decisions, such as weed detection and management, require images with a spatial resolution in the order of one centimeter and, for emergent situations (such as to monitor nutrient stress and disease), a temporal resolution of less than 24 hours (Zhang and Kovacs, 2012).
Airborne sensors are today able to produce data from multispectral to hyperspectral sensors with wavelengths ranging from Vis to MIR, with spatial resolutions ranging from sub-meter to kilometers and with temporal frequencies ranging from 30 min to weeks or months. Significant advancements in unmanned aerial vehicle (UAV) technology as well as in hyperspectral and multispectral sensors (in terms of both weight and image acquisition modes) allow for the combination of these tools to be used routinely for precision agricultural applications. The flexibility of these sensors, their availability and the high achievable spatial resolutions (cm) make them an alternative to satellite sensors. Multispectral sensors embedded on UAV platforms have been used in various agricultural studies, for example, to detect diseases in citrus trees (Garcia-Ruiz et al., 2013), grain yield in rice (Zhou et al., 2017) and for mapping vineyard vigor (Primicerio et al., 2012). UAV systems with multispectral imaging capability are used routinely by companies to estimate the nitrogen needs of plants. This information, given in near real-time to farmers, helps them to make decisions about management. Information extracted from airborne images are also used for precision farming to enhance planning of agricultural interventions or management of agricultural production at the scale of farm fields.
Ground-based spectroscopic sensors have also been developed for agricultural purposes. They collect reflectance data from short distances and can be mounted on tractors or held by hand. For example, the Dualex Force A hand-tool leaf clip (https://www.force-a.com/fr/produits/dualex) is adapted to determine the optical absorbance of the epidermis of a leaf in the ultraviolet (UV) optical range through the differential measurement of the fluorescence of chlorophyll as well as the chlorophyll content of the leaf using different wavelengths in the red and NIR ranges. Using internal model calibration, this tool calculates leaf chlorophyll content, epidermal UV-absorbance and a nitrogen balance index (NBI). This information could then be used to obtain valuable indicators of nitrogen fertilization, plant senescence, or pathogen susceptibility. Other examples are the nitrogen sensors developed by Yara (https://www.yara.fr/fertilisation/outils-et-services/n-sensor/) that enable adjustment of the nitrogen application rate in real time and at any point of the field, according to the crop’s needs.
Food-Related Applications
Conventional, non-imaging, spectroscopic methods are widely used for routine analysis and process control in the agri-food industry. For example, NIR spectroscopy is commonly used in the prediction of protein, moisture, and fat content in a wide range of raw materials and processed products, such as liquids, gels, and powders (Porep et al., 2015). Ultraviolet-Vis (UV-Vis) spectroscopy is a valuable tool in monitoring bioprocesses, such as the development of colored phenolic compounds during fermentation of grapes in the process of winemaking (Aleixandre-Tudo et al., 2017). The Beer-Lambert law (Equation 2.2.9) can be used to predict the concentration of a given compound given its absorbance at a specific wavelength.
While conventional spectroscopic methods are useful for characterizing homogeneous products, the lack of spatial resolution leads to an incomplete assessment of heterogeneous products, such as many foodstuffs. This is particularly problematic in the case of surface contamination, where information on the location, extent, and distribution of contaminants over a food sample is required. Applications of Vis-NIR spectral imaging for food quality and safety are widespread in the scientific literature and are emerging in the commercial food industry. The heightened interest in this technique is driven mainly by the non-destructive and rapid nature of spectral imaging, and the potential to replace current labor- and time-intensive analytical methods in the production process.
This section provides a brief overview of the range and scope of such applications. For a more comprehensive description of these and related applications, several informative reviews have been published describing advances in hyperspectral imaging for contaminant detection (Vejarano et al., 2017), food authentication (Roberts et al., 2018), and food quality control (Gowen et al. 2007; Baiano, 2017).
Contaminant Detection
The ability of spectral imaging to detect spatial variations over a field of view, combined with chemical sensitivity, makes it a promising tool for contaminant detection. The main contaminants that can be detected in the food chain using Vis-NIR include polymers, paper, insects, soil, bones, stones, and fecal matter. Diffuse reflectance is by far the most common mode of spectral imaging utilized for this purpose, meaning that primarily only surface or peripheral contamination can be detected. Of concern in the food industry is the growth of spoilage and pathogenic microorganisms at both pre-harvest and post-harvest processing stages, since these result in economic losses and potentially result in risks to human health. Vis-NIR spectral imaging methods have been demonstrated for pre-harvest detection of viral infection and fungal growth on plants, such as corn (maize) and wheat. For instance, decreases in the absorption of light in wavebands related to chlorophyll were found to be related to the destruction of chloroplasts in corn ears due to Fusarium infection (Bauriegel et al., 2011). Fecal contamination acts as a favorable environment for microbial growth, thus many studies have focused on the detection of such contamination over a wide variety of foods, including fresh produce, meat, and poultry surfaces. For example, both fluorescence and reflectance modalities have been shown to be capable of detecting fecal contamination on apples with high accuracy levels (Kim et al., 2007). Recent studies have utilized spectral imaging transmittance imaging for insect detection within fruits and vegetables, resulting in high detection levels (>80% correct classification) (Vejarano et al., 2017).
Food Authentication
Food ingredient authentication is necessary for the ever expanding global supply chain to ensure compliance with labeling, legislation, and consumer demand. Due to the sensitivity of vibrational spectroscopy to molecular structure and the development of advanced multivariate data analysis techniques such as chemometrics, NIR and MIR spectroscopy have been used successfully in authentication of the purity and geographical origin of many foodstuffs, including honey, wine, cheese, and olive oil. Spectral imaging, having the added spatial dimension, has been used to analyze non-homogeneous samples, where spatial variation could improve information on the authentication or prior processing of the food product, for example, in the detection of fresh and frozen-thawed meat or in adulteration of flours (Roberts et al., 2018).
Food Quality Control
Vis-NIR spectral imaging has been applied in a wide range of food quality control issues, such as bruise detection in mushrooms, apples, and strawberries, and in the prediction of the distribution of water, protein, or fat content in heterogeneous products such as meat, fish, cheese, and bread (Liu et al., 2017). The dominant feature in the NIR spectrum of high moisture foods is the oxygen-hydrogen (OH) bond-related peak centered around 1450 nm. The shape and intensity of this peak is sensitive to the local environment of the food matrix, and can provide information on changes in the water present in food products. This is useful since many deteriorative biochemical processes, such as microbial growth and non-enzymatic browning, rely on the availability of free water in foods. Vis-NIR spectral imaging has also been applied to quality assessment of semi-solid foods, as reviewed by Baiano (2017). For instance, transmittance spectral imaging has been used to non-destructively assess the interior quality of eggs (Zhang et al., 2015), while diffuse reflectance spectral imaging has been used to study the microstructure of yogurt (Skytte et al., 2015) and milk products (Abildgaard et al., 2015).
Examples
Example \(\PageIndex{1}\)
Example 1: Using the Beer-Lambert law to predict the concentration of an unknown solution
Problem:
Data were obtained from a UV-Vis optical absorption instrument, as shown in Table 2.2.2. Light absorbance was measured at 520 nm for different concentrations of a compound that has a red color. The path length was 1 cm. The goal is to use the Beer-Lambert law to calculate the molar absorptivity coefficient and determine the concentration of an unknown solution that has an absorbance of 1.52.
| Concentration (mol L−1) | Absorbance at 520 nm |
|---|---|
|
0.001 |
0.21 |
|
0.002 |
0.39 |
|
0.005 |
1.01 |
|
0.01 |
2.02 |
Solution
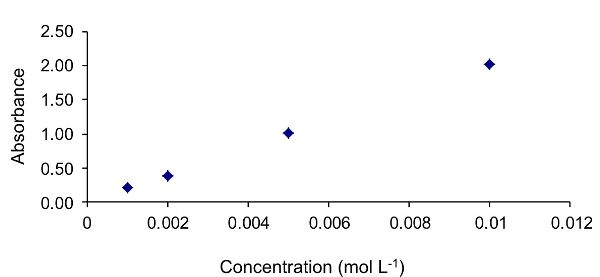
The first step required in calculating the molar absorptivity coefficient is to plot a graph of absorbance as a function of concentration, as shown in Figure 2.2.9. The data follow a linear trend, indicating that the assumptions of the Beer-Lambert law are satisfied.
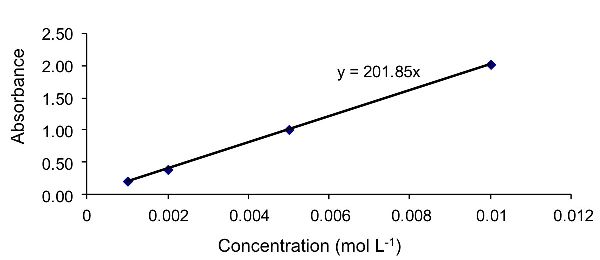
To calculate the molar absorptivity coefficient, it is first necessary to calculate the line of best linear fit to the data. This is achieved here using the “add trendline” function in Excel. The resultant line of best fit is shown in Figure 2.2.10. The equation of this line is y = 201.85x.
Compare this equation to the Beer-Lambert law (Equation 2.2.9):
\( A=\epsilon bC \) (Equation \(\PageIndex{9}\)
where A = absorbance (unitless)
ε = molar absorptivity or molar extinction coefficient = Beer-Lambert proportionality constant (L mol−1 cm−1)
b = path length of the sample (cm)
C = concentration (mol L−1)
In this example, ε b = 201.85, where b is the path length, defined in the problem as 1 cm. Consequently, ε = 201.85 (L mol−1 cm−1). To calculate the concentration of the unknown solution, substitute the absorbance of the unknown solution (1.52) into the equation of best linear fit, resulting in a concentration of 0.0075 mol L−1.
This type of calculation can be used for process or quality control in the food industry or for environmental monitoring such as water quality assessment.
Example \(\PageIndex{2}\)
Example 2: Calculation of vegetation indices from a spectral image
Problem:
The Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) developed by the National Aeronautics and Space Administration (NASA) is one of the foremost spectral imaging instruments for Earth remote sensing (NASA, n. d.). An agricultural scene was gathered by flying over the Indian Pines test site in northwestern Indiana (U.S.) and consists of 145 × 145 pixels and 224 spectral reflectance bands in the wavelength range 400–2500 nm. The Indian Pines scene (freely available at https://doi.org/10.4231/R7RX991C; Baumgardner et al., 2015) contains two-thirds agricultural land and one-third forest or other natural perennial vegetation. There are also two major dual lane highways and a rail line, as well as some low-density housing, other structures, and smaller roads present in the scene. The ground truth image shows the designation of various plots and regions in the scene, and is designated into sixteen classes, as shown in Figure 2.2.11. The average radiance spectrum of four classes of land cover in the scene is plotted in Figure 2.2.12. Table 2.2.3 shows the data corresponding to the plots shown in Figure 2.2.11. Using the mean radiance values, calculate the NDVI and NDWI for each class of land cover. Please note: In this example, the mean radiance values are being used for illustration purposes. This simplification is based on the assumption that the radiation receipt is constant across all wavebands so radiance is assumed to be linearly proportional to reflectance (ratio of reflected to total incoming energy). Typically, vegetation indices are calculated from pixel-level reflectance spectra.
| Grass-Pasture | Grass-Trees | Grass-Pasture-Mowed | Hay-Windrowed | Stone-Steel Towers | |
|---|---|---|---|---|---|
|
NDVI |
0.38 |
0.24 |
0.03 |
0.09 |
−0.25 |
|
NDWI |
0.5 |
0.38 |
0.45 |
0.35 |
0.35 |
By applying the calculation to each pixel spectrum in the image, it is possible to create images of the NDVI and NDWI, as shown in Figure 2.2.13. The NDVI highlights regions of vegetation in red, regions of crop growth and soil in light green-blue, and regions of stone in darker blue. The NDWI, sensitive to changes in water content of vegetation canopies, shows regions of high water content in red, irregularly distributed in the wooded regions.
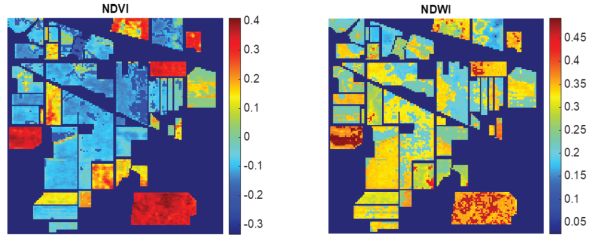
Image Credits
Figure 1. Gorretta, N. (CC By 4.0). (2020). Schematic of a sinusoidal wave described by its wavelength.
Figure 2. Gorretta, N. (CC By 4.0). (2020). Electromagnetic spectrum.
Figure 3. Gorretta, N. (CC By 4.0). (2020). Simplified energy diagram showing (a) absorption, (b) emission of a photon by a molecule, (c) diffusion process.
Figure 4. Gorretta, N. (CC By 4.0). (2020). Absorption of light by a sample.
Figure 5. Gorretta, N. (CC By 4.0). (2020). Schematic diagram showing the path of light for different modes of light measurement, i.e. (a) transmission, (b) reflection, and (c) diffuse reflection.
Figure 6. Gorretta, N. (CC By 4.0). (2020). Spectrometer configuration: transmission diffraction grating.
Figure 7. Gorretta, N. (CC By 4.0). (2020). Hyperspectral imaging sensing mode: (a) reflectance mode, (b) transmission mode.
Figure 8. Gorretta, N. (CC By 4.0). (2020). A green vegetation spectrum.
Figure 9. Gowen, A. A. (CC By 4.0). (2020). Plot of absorbance at 520 nm as a function of concentration.
Figure 10. Gowen, A. A. (CC By 4.0). (2020). Plot of absorbance at 520 nm as a function of concentration showing line and equation of best linear fit to the data.
Figure 11. Gowen, A. A. (CC By 3.0). (2015). Indian Pines ground truth image showing various plots and regions in the scene, designated into sixteen classes. Citation might be: Baumgardner, M. F., L. L. Biehl, and D. A. Landgrebe. 2015. “220 Band AVIRIS Hyperspectral Image Data Set: June 12, 1992 Indian Pine Test Site 3.” Purdue University Research Repository. doi:10.4231/R7RX991C. This item is licensed CC BY 3.0.
Figure 12. Gowen, A. A. (CC By 4.0). (2020). Indian Pines average reflectance spectrum of four classes of land cover in the scene shown in figure 11.
Figure 13. Gowen, A. A. (CC BY 4.0). (2020). NDVI and NDWI calculation of Indian Pines images.
References
Abildgaard, O. H., Kamran, F., Dahl, A. B., Skytte, J. L., Nielsen, F. D., Thomsen, C. L., . . . Frisvad, J. R. (2015). Non-invasive assessment of dairy products using spatially resolved diffuse reflectance spectroscopy. Appl. Spectrosc., 69(9), 1096–1105. https://doi.org/10.1366/14-07529.
Aleixandre-Tudo, J. L., Buica, A., Nieuwoudt, H., Aleixandre, J. L., & du Toit, W. (2017). Spectrophotometric analysis of phenolic compounds in grapes and wines. J. Agric. Food Chem., 65(20), 4009-4026. https://doi.org/10.1021/acs.jafc.7b01724.
Asner, G. P. (1998). Biophysical and biochemical sources of variability in canopy reflectance. Remote Sensing Environ., 64(3), 234-253. https://doi.org/10.1016/S0034-4257(98)00014-5.
Baiano, A. (2017). Applications of hyperspectral imaging for quality assessment of liquid based and semi-liquid food products: A review. J. Food Eng., 214, 10-15. https://doi.org/10.1016/j.jfoodeng.2017.06.012.
Bauer, M. E., & Cipra, J. E. (1973). Identification of agricultural crops by computer processing of ERTS MSS Data. Proc. Symp. on Significant Results Obtained from the Earth Resources Technology Satellite. Retrieved from http://agris.fao.org/agris-search/search.do?recordID=US201302721443.
Baumgardner, M. F., Biehl, L. L., & Landgrebe, D. A. (2015). 220 Band AVIRIS hyperspectral image data set: June 12, 1992 Indian Pine Test Site 3. Purdue University Research Repository. https://doi.org/10.4231/R7RX991C.
Bauriegel, E., Giebel, A., & Herppich, W. B. (2011). Hyperspectral and chlorophyll fluorescence imaging to analyse the impact of Fusarium culmorum on the photosynthetic integrity of infected wheat ears. Sensors, 11(4), 3765-3779. https://doi.org/10.3390/s110403765.
Bohr, N. (1913). I. On the constitution of atoms and molecules. London Edinburgh Dublin Philosophical Magazine J. Sci., 26(151), 1-25. https://doi.org/10.1080/14786441308634955.
Bursey, M. M. (2017). A brief history of spectroscopy. Access Science. https://doi.org/10.1036/1097-8542.BR0213171.
De Broguie, L. V. 1925. On the theory of quanta. Paris, France.
Doraiswamy, P. C., Moulin, S., Cook, P. W., & Stern, A. (2003). Crop yield assessment from remote sensing. Photogrammetric Eng. Remote Sensing, 69(6), 665-674. doi.org/10.14358/PERS.69.6.665.
Farmstar. (n. d.). Farmstar: Have everything you need to manage your crops! Retrieved from www.myfarmstar.com/web/en.
Force A. (n. d.). Dualex scientific. Retrieved from https://www.force-a.com/fr/produits/dualex.
Gao, B.-c. (1996). NDWI: A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sensing Environ., 58(3), 257-266. https://doi.org/10.1016/S0034-4257(96)00067-3.
Garcia-Ruiz, F., Sankaran, S., Maja, J. M., Lee, W. S., Rasmussen, J., & Ehsani, R. (2013). Comparison of two aerial imaging platforms for identification of Huanglongbing-infected citrus trees. Comput. Electron. Agric., 91, 106-115. https://doi.org/10.1016/j.compag.2012.12.002.
Gowen, A. A., O’Donnell, C. P., Cullen, P. J., Downey, G., & Frias, J. M. (2007). Hyperspectral imaging—An emerging process analytical tool for food quality and safety control. Trends Food Sci. Technol., 18(12), 590-598. doi.org/10.1016/j.jpgs.2007.06.001.
Huygens, C. (1912). Treatise on light. Macmillan. Retrieved from http://archive.org/details/treatiseonlight031310mbp.
Kim, M. S., Chen, Y.-R., Cho, B.-K., Chao, K., Yang, C.-C., Lefcourt, A. M., & Chan, D. (2007). Hyperspectral reflectance and fluorescence line-scan imaging for online defect and fecal contamination inspection of apples. Sensing Instrumentation Food Qual. Saf., 1(3), 151. doi.org/10.1007/s11694-007-9017-x.
Liu, Y., Pu, H., & Sun, D.-W. (2017). Hyperspectral imaging technique for evaluating food quality and safety during various processes: A review of recent applications. Trends Food Sci. Technol., 69, 25-35. doi.org/10.1016/j.jpgs.2017.08.013.
Mulla, D. J. (2013). Twenty five years of remote sensing in precision agriculture: Key advances and remaining knowledge gaps. Biosyst. Eng., 114(4), 358-371. https://doi.org/10.1016/j.biosystemseng.2012.08.009.
NASA (n. d.). Airborne visible/infrared imaging spectrometer: AVIRIS overview. NASA Jet Propulsion Laboratory, California Institute of Technology. https://www.jpl.nasa.gov/missions/airborne-visible-infrared-imaging-spectrometer-aviris/.
Ollinger, S. V. (2011). Sources of variability in canopy reflectance and the convergent properties of plants. New Phytol., 189(2), 375-394. doi.org/10.1111/j.1469-8137.2010.03536.x.
Osborne, B. G., Fearn, T., Hindle, P. H., & Osborne, B. G. (1993). Practical NIR spectroscopy with applications in food and beverage analysis (Vol. 2). Longman Scientific & Technical.
Pasquini, C. (2003). Near infrared spectroscopy: Fundamentals, practical aspects and analytical applications. J. Brazilian Chem. Soc., 14(2), 198-219. https://doi.org/10.1590/S0103-50532003000200006.
Pasquini, C. (2018). Near infrared spectroscopy: A mature analytical technique with new perspectives: A review. Anal. Chim. Acta, 1026, 8-36. https://doi.org/10.1016/j.aca.2018.04.004.
Pavia, D. L., Lampman, G. M., Kriz, G. S., & Vyvyan, J. A. (2008). Introduction to spectroscopy. Cengage Learning.
Porep, J. U., Kammerer, D. R., & Carle, R. (2015). On-line application of near infrared (NIR) spectroscopy in food production. Trends Food Sci. Technol., 46(2, Part A), 211-230. doi.org/10.1016/j.jpgs.2015.10.002.
Primicerio, J., Di Gennaro, S. F., Fiorillo, E., Genesio, L., Lugato, E., Matese, A., & Vaccari, F. P. (2012). A flexible unmanned aerial vehicle for precision agriculture. Precision Agric., 13(4), 517-523. doi.org/10.1007/s11119-012-9257-6.
Roberts, J., Power, A., Chapman, J., Chandra, S., & Cozzolino, D. (2018). A short update on the advantages, applications and limitations of hyperspectral and chemical imaging in food authentication. Appl. Sci., 8(4), 505. https://doi.org/10.3390/app8040505.
Rouse Jr., J. W., Haas, R. H., Schell, J. A., & Deering, D. (1974). Monitoring vegetation systems in the Great Plains with ERTS. NASA Special Publ. 351.
Schuster, A. (1911). Encyclopedia Britannica, 2:477.
Skytte, J., Moller, F., Abildgaard, O., Dahl, A., & Larsen, R. (n. d.). Discriminating yogurt microstructure using diffuse reflectance images. Proc. Scandinavian Conf. on Image Analysis (pp. 192-203). Springer. doi.org/10.1007/978-3-319-19665-7_16.
Sun, D.-W. (2009). Infrared spectroscopy for food quality analysis and control. Academic Press.
Thomas, N. C. (1991). The early history of spectroscopy. J. Chem. Education, 68(8), 631. https://doi.org/10.1021/ed068p631.
Remote Sensing, 10(2). https://doi.org/10.3390/rs10020157.
Vejarano, R., Siche, R., & Tesfaye, W. (2017). Evaluation of biological contaminants in foods by hyperspectral imaging: A review. Int. J. Food Properties, 20(sup2), 1264-1297. doi.org/10.1080/10942912.2017.1338729.
Zhang, C., & Kovacs, J. M. (2012). The application of small unmanned aerial systems for precision agriculture: A review. Precision Agric., 13(6), 693-712. doi.org/10.1007/s11119-012-9274-5.
Zhang, W., Pan, L., Tu, S., Zhan, G., & Tu, K. (2015). Non-destructive internal quality assessment of eggs using a synthesis of hyperspectral imaging and multivariate analysis. J. Food Eng., 157, 41-48. https://doi.org/10.1016/j.jfoodeng.2015.02.013.
Zhou, X., Zheng, H. B., Xu, X. Q., He, J. Y., Ge, X. K., Yao, X., . . . Tian, Y. C. (2017). Predicting grain yield in rice using multi-temporal vegetation indices from UAV-based multispectral and digital imagery. ISPRS J. Photogrammetry Remote Sensing, 130, 246-255. https://doi.org/10.1016/j.isprsjprs.2017.05.003.


