2.3: Data Processing in Biosystems Engineering
- Page ID
- 46844
Yao Ze Feng
College of Engineering, Huazhong Agricultural University and Key Laboratory of Agricultural Equipment in Mid-lower Yangtze River, Ministry of Agriculture and Rural Affairs Wuhan, Hubei, China
Variables
Introduction
Novel sensing technologies and data processing play a very important role in most scenarios across the wide varieties of biosystems engineering applications, such as environmental control and monitoring, food processing and safety control, agricultural machinery design and its automation, and biomass and bioenergy production, particularly in the big data era. For instance, to achieve automatic, non-destructive grading of agricultural products according to their physical and chemical properties, raw data from different types of sensors should be acquired and carefully processed to accurately describe the samples so that the products can be classified into different categories correctly (Gowen et al., 2007; Feng et al., 2013; O’Donnell et al., 2014; Baietto and Wilson, 2015; Park and Lu, 2016). For the environmental control of greenhouses, temperature, humidity, and the concentration of particular gases should be determined by processing the raw data acquired from thermistors, hydrometers, and electronic noses or optical sensors (Bai et al., 2018). Successful use of measurements relies heavily on data processing that converts the raw data into meaningful information for easier interpretation and understanding the targets of interest.
The purpose of data processing is to turn raw data into useful information that can help understand the nature of objects or a process. To make this whole procedure successful, particular attention should be paid to ensure the quality of raw data. However, the raw data obtained from biological systems are always affected by environmental factors and the status of samples. For example, the optical profiles of meat are vulnerable to temperature variation, light conditions, breeds, age and sex of animals, type of feeds, and geographical origins, among other factors. To ensure the best quality of raw data, data pretreatment is essential.
In this chapter, data pretreatment methods, including smoothing, derivatives, and normalization, are introduced. With good quality data, a modeling process correlating the raw data with features of the object or process of interest can be developed. This can be realized by employing different modeling methods. After validation, the established model can then be used for real applications.
Outcomes
After reading this chapter, you should be able to:
- • Describe the principles of various data processing methods
- • Determine appropriate data processing methods for model development
- • Evaluate the performance of established models
- • List examples of the application of data processing
Concepts
Data Pretreatment
Data Smoothing
To understand the features of biological objects, different sensors or instruments can be employed to acquire signals representing their properties. For example, a near-infrared (NIR) spectrometer is used to collect the optical properties across different wavelengths, called the spectrum, of a food or agricultural product. However, during signal (i.e., spectrum) acquisition, random noise will inevitably be introduced, which can deteriorate signal quality. For example, short-term fluctuations may be present in signals, which may be due to environmental effects, such as the dark current response and readout noise of the instrument. Dark current is composed of electrons produced by thermal energy variations, and readout noise refers to information derived from imperfect operation of electronic devices. Neither of them contribute to the understanding of the objects under investigation. In order to decrease such effects, data smoothing is usually applied. Some popular data smoothing methods include moving average (MV) and S-G (Savitzky and Golay) smoothing.
The idea of moving average is to apply “sliding windows” to smooth out random noises at each segment of the signal by calculating the average value in the segment so that the random noise in the whole signal can be reduced. Given a window with an even number of data points at a certain position, the average value of the original data within the window is calculated and used as the smoothed new value for the central point position. This procedure is repeated until reaching the end of the original signal. For the data points at the two edges of the signal that cannot be covered by a complete window, one can still assume the window is applied but only calculate the average of the data available in the window. The width of window is a key factor that should be determined carefully. It is not always true that the signal-to-noise ratio increases with window width since a too-large window will tend to smooth out useful signal as well. Moreover, since the average value is calculated for each window, all data points in the window are considered as equal contributors for the signal; this will sometimes result in signal distortion. To avoid this problem, S-G smoothing can be introduced.
Instead of using a simple average in the moving average process, Savitzky and Golay (1964) proposed assigning weights to different data in the window. Given an original signal X, the smoothed signal XS can be obtained as:
\[ XS_{i}=\frac{\sum^{r}_{j=-r} X_{i+j}W_{j}}{\sum{^{r}_{j=-r}W_{j}}} \]
where 2r + 1 is window width and Wi is the weight for the ith data point in the window. W is obtained by fitting the data points in the window to a polynomial form following the least squares principle to minimize the errors between the original signal X and the smoothed signal XS and calculating the central points of the window from the polynomial. In applying S-G smoothing, the smoothing points and order of polynomials should be decided first. Once the two parameters are determined, the weight coefficients can then be applied to the data points in the window to calculate the value of the central point using Equation 2.3.1.
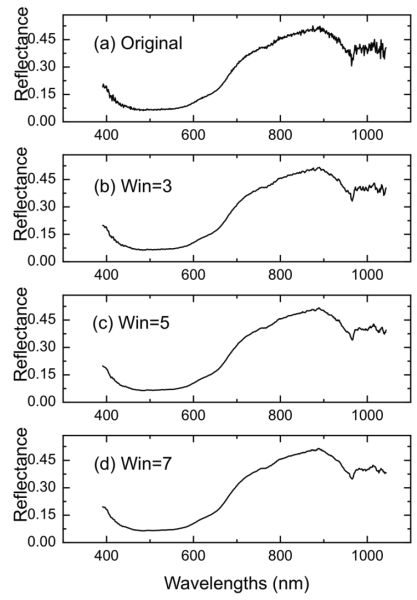
Figure 2.3.1 shows the smoothing effect by applying S-G smoothing to a spectrum of beef sample (Figure 2.3.1b-d). It is clearly shown that after S-G smoothing, the random noise in the original signal (Figure 2.3.1a) is greatly suppressed when the window width is 3 (Figure 2.3.1b). An even better result is achieved when the window width increases to 5 and 7, where the curve becomes smoother (Figure 2.3.1d) and the short fluctuations are barely seen.
Derivatives
Derivatives are methods for recovering useful information from data while removing slow change of signals (or low frequency signals) that could be useless in determining the properties of biological samples. For example, for a spectrum defined as a function y = f(x), the first and second derivatives can be calculated as:
\[ \frac{dy}{dx} = \frac{f(x+\Delta x)-f(x)}{\Delta x} \]
From Equations 2.3.2 and 2.3.3, it can be understood that the offset (e.g., constant shift of signals) of the signal can be eliminated after first derivative processing, while both offset and slope in the original signal can be excluded after second derivative processing. Specifically, for the first derivative, the constant values (corresponding to the offset) can be eliminated due to the difference operation in the numerator of Equation 2.3.2. After the first derivative, the spectral curve with the same slope can be converted to a new offset and this can be further eliminated by a second derivative. Since offset variations and slope information always indicate environmental effects on the signal and irrelevant factors that are closely correlated with independent variables, application of derivative methods will help reduce such noises. Moreover, processing signals with derivatives offer an efficient approach to enhance the resolution of signals by uncovering more peaks, particularly in spectral analysis.
For biological samples with complicated chemical components, the spectra are normally the combination of different absorbance peaks arising from these components. Such superimposed peaks, however, can be well separated in second derivative spectra. Nevertheless, it should be noted that the signal-to-noise ratio of the signal will deteriorate with the increase of derivative orders since the noise is also enhanced substantially, particularly for the higher order derivatives, though high order derivatives are sometimes found to be useful in understanding the detailed properties of the objects. To avoid noise enhancement, a S-G derivative can be introduced where signal derivatives are attained by computing the derivatives of the polynomial. Specifically, the data points in a sliding window are fitted to a polynomial of a certain order following the procedure of S-G smoothing. Within the window, derivatives of the fitted polynomial are then calculated to produce new weights for the central point. When the sliding window reaches the end of the signal, derivatives of the current signal are then attained.
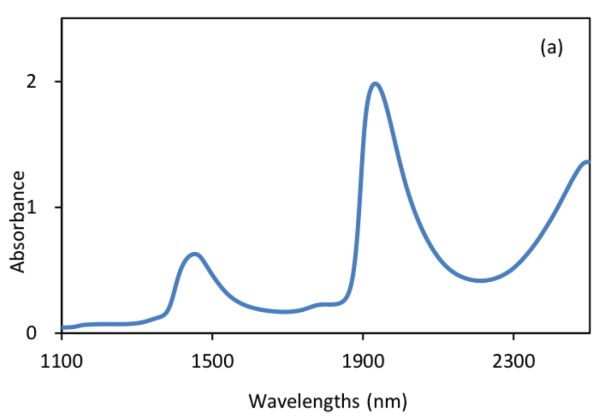
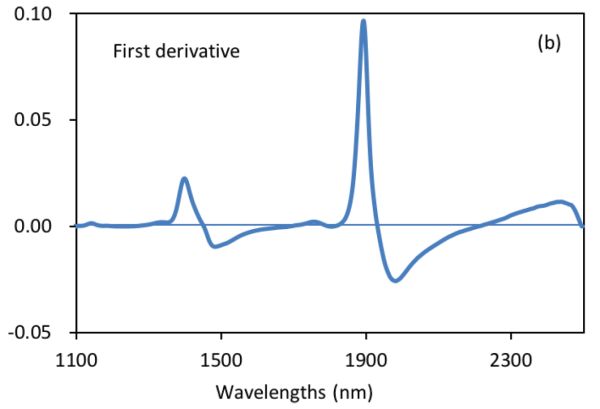
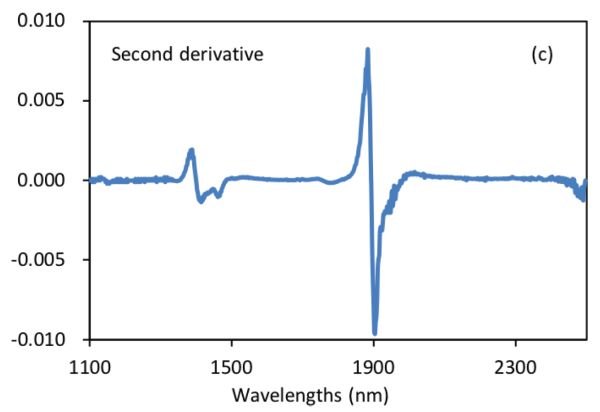
Figure 2.3.2 shows absorbance and derivative spectra of bacterial suspensions (Feng et al., 2015). It is demonstrated that after S-G derivative operation with 5 smoothing points and polynomial order of 2, the constant offset and linear baseline shift in the original spectrum (Figure 2.3.2a) are effectively removed in the first (Figure 2.3.2b) and second (Figure 2.3.2c) derivative spectra, respectively. Particularly, the second derivative technique is also a useful tool to separate overlapped peaks where a peak at ~1450 nm is resolved into two peaks at 1412 and 1462 nm.
Normalization
The purpose of data normalization is to equalize the magnitude of sample signals so that all variables for a sample can be treated equally for further analysis. For example, the surface temperature of pigs and environmental factors (temperature, humidity, and air velocity) can be combined to detect the rectal temperature of sows. Since the values for pig surface temperature can be around 39°C while the air velocity is mostly below 2 m/s, if these values are used directly for further data analysis, the surface temperature will intrinsically play a more dominant role than air velocity does simply due to its larger values. This may lead to biased interpretation of the importance of variables. Data normalization is also helpful when signals from different sensors are combined as variables (i.e., data fusion) to characterize biological samples that are complex in composition and easily affected by environmental conditions. However, since data normalization removes the average as well as the standard deviation of the sample variables, it might give confusing information about the samples if variabilities of variables in different units are important in characterizing sample properties.
Standard normal variate (SNV), or standardization, is one of the most popular methods used to normalize sample data (Dhanoa et al., 1994). Given a sample data X, the normalized Xnor can be obtained as:
\[ X_{nor}=\frac{X-mean(X)}{SD(X)} \]
where mean(X) and SD(X) are the mean and standard deviation of X, respectively.
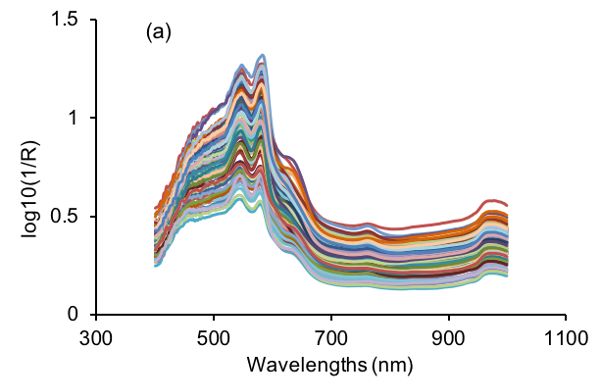
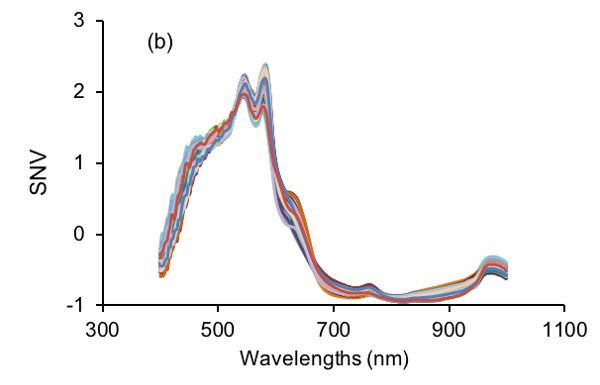
After SNV transformation, a new signal with a mean value of 0 and unit standard deviation is produced. Therefore, SNV is useful in eliminating dimensional variance among variables since all variables are compared at the same level. In addition, as shown in Figure 2.3.3, SNV is capable of correcting the scattering effect of samples due to physical structure of samples during light-matter interactions (Feng and Sun, 2013). Specifically, the large variations in visible NIR (vis-NIR) spectra of beef samples (Figure 2.3.3a) are substantially suppressed as shown in Figure 2.3.3b.
Modeling Methods
The purpose of modeling in data processing is mainly to establish the relationship between independent variables and dependent variables. Independent variables are defined as stand-alone factors that can be used to determine the values of other variables. Since the values of other variables depend on the independent variables, they are called dependent variables. For example, if size, weight, and color are used to classify apples into different grades, the variables of size, weight, and color are the independent variables and the grade of apples is the dependent variable. The dependent variables are calculated based on measured independent variables. During model development, if only one independent variable is used, the resultant model is a univariate model, while two or more independent variables are involved in multivariate models. If dependent variables are used during model calibration or training, the methods applied in model development are termed supervised. Otherwise, an unsupervised method is employed. The dataset used for model development is called the calibration set (or training set) and a new dataset where the model is applied for validation is the validation set (or prediction set).
The developed models can be used for different purposes. Basically, if the model is used to predict a discrete class (categorical), it is a classification model; and if it aims to predict a continuous quantity, it is a regression model. For instance, if spectra of samples are used to identify the geographical origins of beef, the spectra (optical properties at different wavelengths) are the independent variables and the geographical origins are the dependent variables. The established multivariate model describing the relationship between spectra and geographical origins is a classification model. In a classification model, the dependent variables are dummy variables (or labels) where different arbitrary numbers are used to represent different classes but with no physical meaning. On the other hand, if spectra of samples are used to determine the water content of beef, the developed model is then a regression model. The dependent variables are meaningful numbers indicating the actual water content. Simply, a classification model tries to answer the question of “What is it?” and a regression model tries to determine “How much is there?” There is a wide range of methods for regression or classification models. Some are described below.
Linear Regression
Linear regression is an analytical method that explores the linear relationship between independent variables (X) and dependent variables (Y). Simple linear regression is used to establish the simplest model that can be used to illustrate the relationship between one independent variable X and one dependent variable Y. The model can be described as:
\[ y = \beta_{0}+\beta_{1}X+E \]
where X is the independent variable; Y is the dependent variable; \(\beta_{0}\), \(\beta_{1}\), are the regression coefficients; and E is the residual vector.
Simple linear regression is used when only one independent variable is to be correlated with the dependent variable. In the model, the two important coefficients, \(\(\beta_{0}\) and \(\beta_{1}\), can be determined by finding the best fit line through the scatter curve between X and Y via the least squares method. The best fit line requires minimization of errors between the real Y and the predicted \(\hat{Y}\). Since the errors could be either positive or negative, it is more appropriate to use the sum of squared errors. Based on this, \(\beta_{0}\) and \(\beta_{1}\) can be calculated as:
\[ \beta_{1}=\frac{\sum^{n}_{i=1}(X_{i}-\bar{X})(Y_{i}-\bar{Y})}{\sum^{n}_{i=1}(X_{i}-\bar{X})^{2}} \]
\[ \beta_{0}=\bar{Y}-\beta_{1}\bar{X} \]
where \(\bar{X}\) and \(\bar{Y}\) are mean values of X and Y, respectively, and n is the number of samples.
Multiple linear regression (MLR) is a linear analysis method for regression in which the corresponding model is established between multiple independent variables and one dependent variable (Ganesh, 2010):
\[ Y=\beta_{0}+\sum^{n}_{j=i}\beta_{j}X_{j}+E \]
where \(X_{j}\) is the \(j^{th}\) independent variable; Y is the dependent variable; \(\beta_{0}\) is the intercept; \(\beta_{1}\), \(\beta_{2}\), . . . , \(\beta_{n}\) are regression coefficients, and E is the residual matrix.
Although MLR tends to give better results compared with simple linear regression since more variables are utilized, MLR is only suitable for situations where the number of variables is less than the number of samples. If the number of variables exceeds the number of samples, Equation 2.3.8 will be underdetermined and infinite solutions can be produced to minimize residuals. Therefore, multiple linear regression is generally employed based on important feature variables (such as important wavelengths in spectral analysis) instead of all variables, if the number of variables is larger than that of samples.
Similar to simple linear regression, the determination of regression coefficients also relies on the minimization of prediction residuals (i.e., the sum of squared residuals between true Y values and predicted \(\hat{Y}\)). Specific procedures can be found elsewhere (Friedman et al., 2001).
Principal Component Analysis (PCA)
Due to the complicated nature of biological samples, data acquired to characterize samples usually involve many variables. For example, spectral responses at hundreds to thousands of wavelengths may be used to characterize the physical and chemical components of samples. Such great dimensionality inevitably brings difficulties in data interpretation. With the original multivariate data, each independent variable or variable combinations can be used to draw one-, two-, or three-dimensional plots to understand the distribution of samples. However, this process requires a huge workload and is unrealistic if more than three variables are involved.
Principal component analysis (PCA) is a powerful tool to compress data and provides a much more efficient way for visualizing data structure. The idea of PCA is to find a set of new variables that are uncorrelated with each other and attach the most data information onto the first few variables (Hotelling, 1933). Initially, PCA tries to find the best coordinate that can represent the most data variations in the original data and record it as PC1. Other PCs are subsequently extracted to cover the greatest variations of the remaining data. The established PCA model can be expressed as:
\[ X=TP^{T}+E \]
where X is the independent variable matrix, T is the score matrix, PT is the loading matrix, and E is the residual matrix. The score matrix can be used to visualize the relationship between samples and the loadings can be used to express the relations between variables.
After PCA, the data can be represented by a few PCs (usually less than 10). These PCs are sorted according to their contribution to the explanation of data variance. Specifically, an accumulated contribution rate, defined as explained variance from the first few PCs over the total variance of the data, is usually employed to evaluate how many new variables (PCs) should be used to represent the data. Nevertheless, by applying PCA, the number of variables required for characterizing data variance is substantially reduced. After projecting the original data into the new PC spaces, data structure can be easily seen, if it exists.
Partial Least Squares Regression (PLSR)
As illustrated above, MLR requires that the number of samples be more than the number of variables. However, biological data normally contain far more variables than samples, and some of these variables may be correlated with each other, providing redundant information. To cope with this dilemma, partial least squares regression (PLSR) can be used to reduce the number of variables in the original data while retaining the majority of its information and eliminating redundant variations (Mevik et al., 2011). In PLSR, both X and Y are projected to new spaces. In such spaces, the multidimensional direction of X is determined to best account for the most variance of multidimensional direction of Y. In other words, PLSR decomposes both predictors X and dependent variable Y into combinations of new variables (scores) by ensuring the maximum correlation between X and Y (Geladi and Kowalski, 1986). Specifically, the score T of X is correlated with Y by using the following formulas:
\[ Y= XB+ E=XW^{*}_{a}C+E=TC+E \]
\[ W^{*}_{a}=W_{a}(P^{T}W_{a})^{-1} \]
where B is the regression coefficients for the PLSR model established; E is the residual matrix; Wa represents the PLS weights; a is the desired number of new variables adopted; P and C are loadings for X and Y, respectively. The new variables adopted are usually termed as latent variables (LVs) since they are not the observed independent variables but inferred from them.
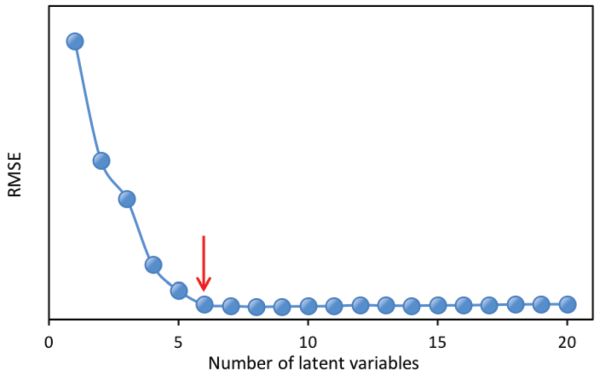
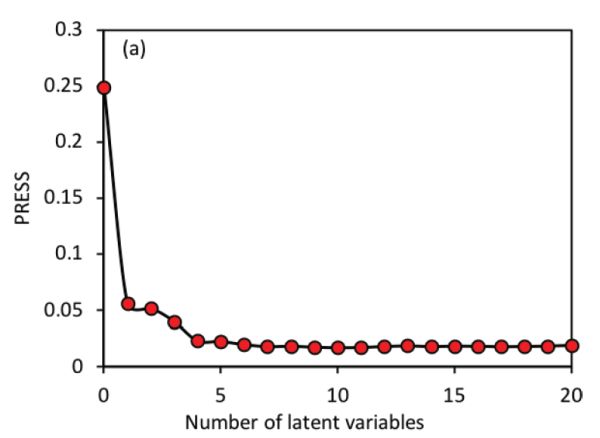
The most important parameter in PLS regression is the determination of the number of LVs. Based on the PLSR models established with different LVs, a method named leave-one-out cross validation is commonly utilized to validate the models. That is, for the model with a certain number of LVs, one sample from the data set is left out with the remaining samples used to build a new model. The new model is then applied to the sample that is left out for prediction. This procedure is repeated until every sample has been left out once. Finally, every sample would have two values, i.e., the true value and the predicted value. These two types of values can then be used to calculate root mean squared errors (RMSEs; Equation 2.3.13 in the Model Evaluation section below) for different numbers of LVs. Usually, the optimal number of LVs is determined either at the minimum value of RMSEs or the one after which the RMSEs are not significantly different from the minimum RMSE. In Figure 2.3.4 for instance, using 6 latent variables would produce a very similar RMSE value to the minimum RMSE that is attained with 11 LVs; therefore, 6 latent variables would be more suitable for simpler model development.
In addition to the methods introduced above, many more algorithms are available for model development. With the fast growth of computer science and information technologies, modern machine learning methods, including artificial neural networks, deep learning, decision trees, and support vector machines, are widely used in biosystems engineering (LeCun et al., 2015; Maione and Barbosa, 2019; Pham et al., 2019, Zhao et al., 2019).
The model development methods described above can be used for both regression and classification problems. For regression, the final outputs are the results produced when the independent variables are input into the established models. For classification, a further operation is required to attain the final numbers for categorical representation. Normally, a rounding operation is adopted. For instance, a direct output of 1.1 from the model tends to be rounded down to 1 as the final result, which can be a label for a certain class. After such modification, the name of the regression method can be changed from PLSR to partial least squares discriminant analysis (PLS-DA), as an example. However, these numbers do not have actual physical meanings, and therefore they are often termed dummy variables.
Since a model can be established using different modeling methods, some of which are outlined above, the decision on which type of method to use is task-specific. If the objective is to achieve stable model with high precision, the one that can lead to the best model performance should be employed. However, if the main concern is simplicity and easy interpretation based on feasible application, a linear method will often be the best choice. In cases when a linear model fails to depict the correlation between X and Y, nonlinear models established by applying artificial neural networks or support vector machines could then be applied.
Model Evaluation
The full process of model development includes the calibration, validation, and evaluation of models. Model calibration tries to employ different modeling methods to the training data to find the best parameters for representation of samples. For example, if PLSR is applied to NIR spectral data to quantify beef adulteration with pork, the important parameters including the number of LVs and regression coefficients are determined so that when the spectra are inputted to the model, the predicted percentage of adulteration levels can be calculated. It is clear that this process simply works on the training data itself and the resultant model can best explain the data of the particular samples. However, since the modeling process is data specific, good model performance sometimes can be due to the modeling of noise and such models will fail to function with new, independent data. This problem is known as over-fitting and should be always avoided during modeling. Therefore, it is of crucial importance to validate the performance of the models using independent data, i.e., data that are not included in the calibration set and that are totally unknown to the established model.
Model validation is a process to verify whether similar model performance can be attained to that of calibration. There are basically two ways to conduct model validation. One is to use cross-validation, if there are not enough samples available. Cross-validation is implemented based on the training set and often a leave-one-out approach is taken (Klanke and Ritter, 2006). During leave-one-out cross-validation, one sample is left out from the calibration set and a calibration model is developed based on the remaining data. The left-out sample is then inputted to the developed model based on the other samples. This procedure terminates when all samples have been left out once. Finally, all samples will be predicted for comparison with the measured values. However, this method should be used with caution since it may lead to over-optimistic evaluation or model overfitting. Another approach, called external validation, is to introduce an independent prediction set that is not included in the calibration set and apply the model to the new, independent dataset. External validation is always preferred for model evaluation. Nevertheless, it is recommended to apply both cross-validation and external validation methods to evaluate the performance of models. This is particularly important in biosystems engineering because biological samples are very complex and their properties can change with time and environment. For meat samples, the chemical components of meat vary due to species, geographical origins, breeding patterns, and even different body portions of the same type of animal. The packaging atmosphere and temperature also have great influence on the quality variations of meat. Ideally, with a good and stable model, the results from cross-validation and external validation should be similar.
Model evaluation is an indispensable part of model development, which aims to determine the best performance of a model as well as to verify its validity for future applications by calculating and comparing some statistics (Gauch et al., 2003). For regression problems, two common parameters, coefficient of determination (R2), and root mean squared error (RMSE), are calculated to express the performance of a model. They are defined as follows:
\[ R^{2} = 1- \frac{\sum^{n}_{i=1}(Y_{i,meas}-Y_{i,pre})^{2}}{\sum^{n}_{i=1}(\bar{Y}-Y_{i,pre})^{2}} \]
\[ \text{RMSE} = \sqrt{\frac{1}{n} \sum^{n}_{i=1}(Y_{i,meas}-Y_{i,pre})^{2}} \]
where Yi,pre and Yi,meas, respectively, represent the predicted value and the measured value of targets for sample i; is the mean target value for all samples. An R2 of 1 and RMSE of 0 for all data sets would indicate a “perfect” model. Thus, the goal is to have R2 as close to 1 as possible and RMSE close to 0. In addition, a stable model has similar R2 and RMSE values for calibration and validation. It should be noted that R, the square root of R2, or correlation coefficient, is also frequently used to express the linear relationship between the predicted and measured values. Moreover, since different data sets may be used during model development, the above parameters can be modified in accordance. For example, R2C, R2CV and R2P can be used to represent the coefficients of determination for calibration, cross-validation, and prediction, respectively. Root mean squared errors for calibration, cross-validation, and prediction are denoted as RMSEC, RMSECV, and RMSEP, respectively.
For classification problems, a model’s overall correct classification rate (OCCR) is an important index used to evaluate the classification performance:
\[ \text{OCCR} = \frac{\text{Number of correctly classified samples}}{\text{Total number of samples}} \]
The number of correctly classified samples is determined by comparing the predicted classification with the known classification. To investigate the detailed classification performance, a confusion matrix can be utilized (Townsend, 1971). A confusion matrix for binary classifications is shown in Table 2.3.1. In the confusion matrix, true positive and true negative indicate samples that are predicted correctly. False positives and false negatives are encountered when what is not true is wrongly considered as true and vice versa. Based on the confusion matrix, parameters can be attained to evaluate the classification model, including the sensitivity, specificity, and prevalence, among others:
| Condition Positive | Condition Negative | |
|---|---|---|
|
Predicted Positive |
True positive (Power) |
False positive (Type I error) |
|
Predicted Negative |
False negative (Type Il error) |
True negative |
\[ \text{Sensitivity} = \frac{\sum \text{True positive}}{\sum \text{Condition positive}} \]
\[ \text{Specificity} = \frac{\sum \text{True negative}}{\sum \text{Condition negative}} \]
\[ \text{Prevalence} = \frac{\sum \text{Condition positive}}{\sum \text{Total positive}} \]
Applications
Beef Adulteration Detection
Food adulteration causes distrust in the food industry by leading to food waste due to food recall and loss of consumer trust. Therefore, it is crucial to use modern technologies to detect deliberate adulteration or accidental contamination. For example, a handheld spectrometer can be used to obtain spectra from beef samples. The raw spectra can be processed by the spectrometer to quantify the level, if any, of adulteration of each beef sample. To properly process the raw spectra, purposeful contamination experiments can be used to determine the appropriate pretreatment (or preprocessing) method(s) for the raw data. For example, Figure 2.3.5a shows spectra corresponding to different adulteration levels. Adulteration concentration in such an experiment should range from 0% to 100% with 0% being pure fresh beef and 100% for pure spoiled beef. The experiment should include a calibration dataset to develop the predictive relationship from spectra and an independent dataset to test the validity of the prediction. The following process can be used to determine the best preprocessing method for quantification of beef adulteration.
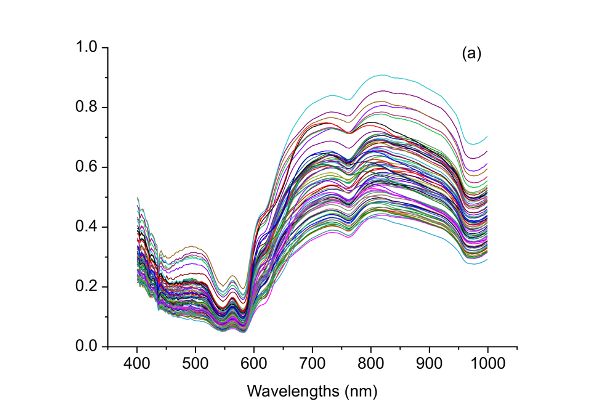
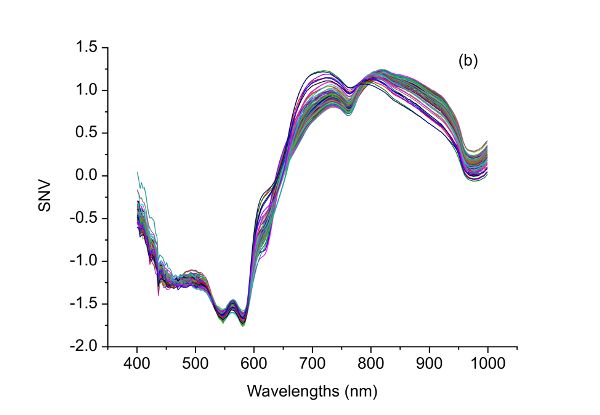
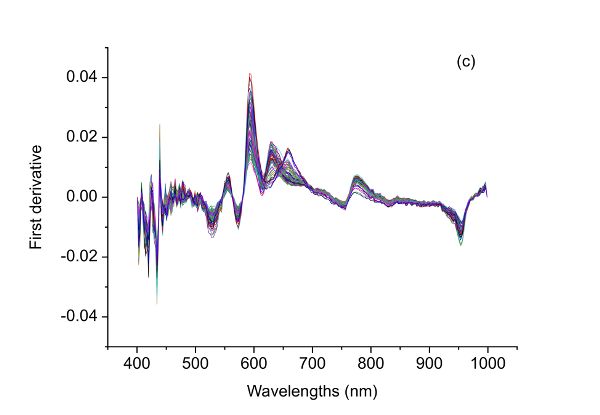
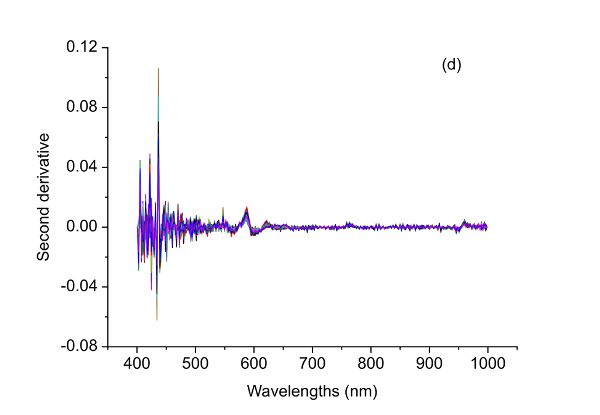
The raw spectral data (Figure 2.3.5a) have what is probably random noise with the signal, particularly at the lower wavelengths (400–500 nm). The reason for saying this is there are variations in spectral magnitude among the samples that do not change linearly with adulteration concentration. It is possible that these variations (noise in this application) are due to differences in chemical components of the samples, since spoiled meat is very different from fresh meat, so when the two are mixed in different proportions a clear signal should be visible. Noise might also be introduced due to small differences in the physical structure of samples causing variation of light scattering between the samples. Also note that there are only limited peaks and there is evident offset in the raw spectra. Therefore, different preprocessing methods including S-G smoothing, SNV, and the first and second derivatives can be applied to the raw spectra (Figure 2.3.5) and their performance in terms of improving the detection of beef adulteration compared.
Table 2.3.2 shows the performance of different preprocessing methods together with PLSR in determining the adulteration concentration. All the preprocessing methods applied lead to better models with smaller RMSEs, although such improvement is not very much. The optimal model was attained by using SNV as the preprocessing method, which had coefficients of determination of 0.93, 0.92, and 0.88 as well as RMSEs of 7.30%, 8.35%, and 7.90% for calibration, cross-validation, and prediction, respectively. Though second derivative spectra have contributed to better prediction precision (7.37%), the corresponding model yielded larger RMSEs for both calibration and cross-validation. Therefore, the best preprocessing method in this case is SNV. This preprocessing method can be embedded in a handheld spectrometer, where the raw spectra of adulterated beef samples acquired can be normalized by removing the average and then dividing by the standard deviation of the spectra. The prediction model can then be applied to the SNV-preprocessed data to estimate levels of beef adulteration and to provide insights into the authenticity of the beef product.
| Methods | RMSEC (%) | RMSECV (%) | RMSEP (%) | R2C | R2CV | R2P | LV |
|---|---|---|---|---|---|---|---|
|
None |
8.35 |
9.34 |
7.99 |
0.91 |
0.90 |
0.88 |
4 |
|
1st Derivative |
8.05 |
8.78 |
7.92 |
0.92 |
0.91 |
0.88 |
3 |
|
2nd Derivative |
7.92 |
10.03 |
7.37 |
0.92 |
0.88 |
0.90 |
4 |
|
SNV |
7.30 |
8.35 |
7.90 |
0.93 |
0.92 |
0.88 |
4 |
|
S-G |
7.78 |
8.90 |
7.91 |
0.93 |
0.91 |
0.88 |
5 |
|
C = calibration CV = coefficient of variation SEP = standard error of prediction P = prediction LV = latent variables |
|||||||
Bacterial Classification
Identification and classification of bacteria are important for food safety, for the design of processes such as thermal treatment, and to help identify the causes of illness when bacterial contamination has occurred. This example outlines how a classification system can be developed (Feng et al., 2015). A spectral matrix was derived by scanning a total of 196 bacterial suspensions of various concentrations using a near infrared spectrometer over two wavelength ranges, i.e., 400–1100 nm and 1100–2498 nm. A column vector that recorded the labels for each bacterium (i.e., its name or classification) was also constructed. This dataset were used to classify different bacteria including three Escherichia coli strains and four Listeria innocua strains. Since the dataset contained a large number (>1000) of variables, it was interesting to visualize the structure of the data to investigate potential sample clustering. By using appropriate modeling methods, it was possible to establish a model for classifying bacteria at species level.
PCA can be used to understand the structure of data. Since the scores of a PCA model can be used to elucidate the distribution of samples, it is interesting to draw a score plot such as Figure 2.3.6. The first two columns of the score matrix T are the scores for the first two PCs and is generated by using the first one as x-axis and the other as y-axis. The loading plots in Figure 2.3.6 can be created by plotting the first two columns of the loading matrix PT versus variable names (wavelengths in this case), respectively.
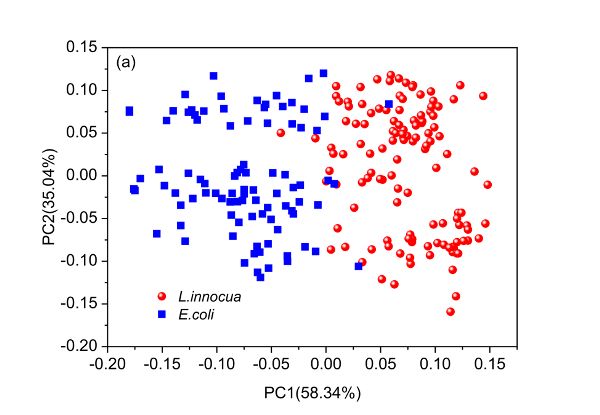
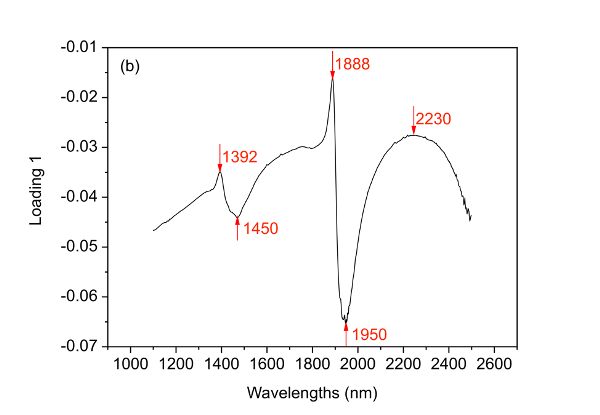
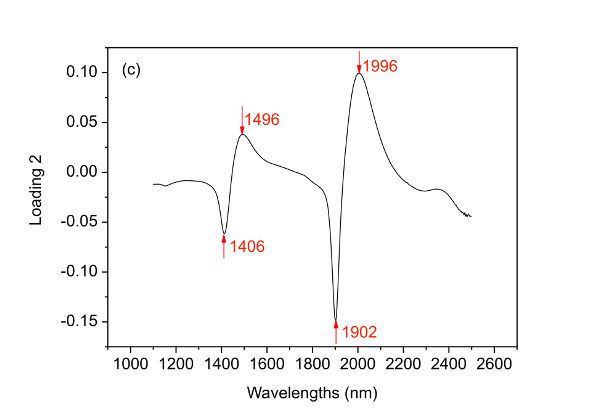
The first and second PCs have covered 58.34% and 35.04% of the total variance of the spectral data set, leading to 93.38% of the information explained. Based on such information, it is demonstrated clearly that the two bacteria are well separated along the first PC though very few samples mixed together. By investigating loading 1, it is found that five main wavelengths including 1392, 1450, 1888, 1950, and 2230 nm are important variables that contribute to the separation of the two bacterial species. Also, it is interesting to find that two clusters appear within either of the two bacterial species and such separation can then be explained by the four major wavelengths indicated in loading 2 (Figure 2.3.6c).
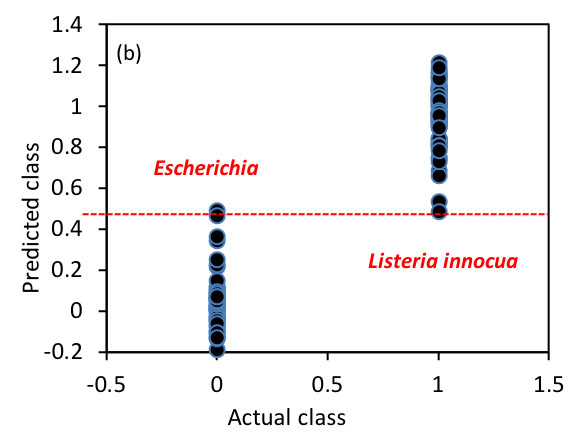
The next target is to establish a classification model in the 400–1100 nm region for the classification of these bacterial species. To achieve this, PLS-DA was employed where the spectral data and the bacterial labels are used as independent and dependent variables, respectively. Figure 2.3.7 shows the performance of the established model. The optimized model takes four latent variables to produce OCCRs of 99.25% and 96.83% for calibration and prediction, respectively. To calculate OCCRs, the predicted values of individual samples are first rounded to get values of 1 or 0 and these predicted labels are then compared with the true labels, following which Equation 2.3.14 is employed.
A confusion matrix showing the classification details for prediction is shown in Table 2.3.3. It shows that the true positive for detecting E. coli and L. innocua are 25 and 36, respectively. Accordingly, the sensitivity for detecting E. coli and L. innocua species are 0.93 (25/27) and 1 (36/36), respectively. All the above parameters for both calibration and prediction demonstrate that the two bacterial species can be well classified.
| Actual Class | Predicted Class | Total | |
|---|---|---|---|
| E. coli | L. innocua | ||
|
E. coli |
25 |
2 |
27 |
|
L. innocua |
0 |
36 |
36 |
|
Total |
25 |
38 |
63 |
In microbial safety inspection of food products, it is important to identify the culprit pathogens that are responsible for foodborne diseases. To achieve this, bacteria on food surfaces can be sampled, cultured, isolated, and suspended, and the model can be applied to the spectra of bacterial suspensions to tell us which of those two species of bacteria are present in the food product.
Examples
Example \(\PageIndex{1}\)
Example 1: Moving average calculation
Problem:
Fruit variety and ripeness of fruit can be determined by non-destructive methods such as NIR spectroscopy. A reflectance spectrum of a peach sample was acquired; part of the spectral data in the wavelength range of 640–690 nm is shown in Table 2.3.4. Though the spectrometer is carefully configured, there still might be noise present in the spectra due to environmental conditions. Apply the moving average method to smooth the spectrum and to reduce potential noise.
Solution
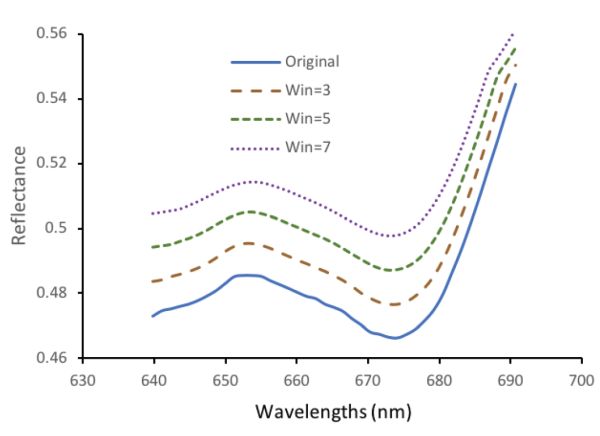
Various software, including Microsoft, MATLAB, and commercial chemometric software (the Unscrambler, PLS Toolbox etc.) are available for implementing the moving average. Taking Microsoft Excel as an example, the “average” function is required. Given a spectrum presented column-wise (for example, column B), the value for the smoothed spectrum at cell B10 can be obtained as average(B9:B11) if the window size is 3, and average(B8:B12) or average(B7:B13) if the window size is 5 or 7, respectively. For both ends of the spectrum, only the average of values present in the window of a particular size is calculated. For instance, the spectral value at 639.8 nm after moving average smoothing under the window size of 3 can be obtained as the mean values of the original spectrum at 639.8, 641.1 and 642.2 nm, that is, (0.4728 + 0.4745 + 0.4751)/3 =0.4741.
Figure 2.3.8 shows the smoothed spectrum, the result of using the moving average method. Note that the spectra are shifted 0.01, 0.02, and 0.03 unit for the Win = 3, Win = 5, and Win = 7 spectra to separate the curves for visual presentation purposes. It is clear that for the original data, there is slight fluctuation and such variation is diminished after moving average smoothing.
| Wavelength (nm) |
Reflectance | Wavelength (nm) |
Reflectance |
|---|---|---|---|
|
639.8 |
0.4728 |
665.2 |
0.4755 |
|
641.1 |
0.4745 |
666.5 |
0.4743 |
|
642.4 |
0.4751 |
667.7 |
0.4721 |
|
643.6 |
0.4758 |
669.0 |
0.4701 |
|
644.9 |
0.4766 |
670.3 |
0.4680 |
|
646.2 |
0.4777 |
671.5 |
0.4673 |
|
647.4 |
0.4791 |
672.8 |
0.4664 |
|
648.7 |
0.4807 |
674.1 |
0.4661 |
|
650.0 |
0.4829 |
675.3 |
0.4672 |
|
651.2 |
0.4850 |
676.6 |
0.4689 |
|
652.5 |
0.4854 |
677.9 |
0.4715 |
|
653.8 |
0.4854 |
679.2 |
0.4747 |
|
655.0 |
0.4851 |
680.4 |
0.4796 |
|
656.3 |
0.4838 |
681.7 |
0.4862 |
|
657.6 |
0.4826 |
683.0 |
0.4932 |
|
658.8 |
0.4814 |
684.3 |
0.5010 |
|
660.1 |
0.4801 |
685.5 |
0.5093 |
|
661.4 |
0.4789 |
686.8 |
0.5182 |
|
662.7 |
0.4782 |
688.1 |
0.5269 |
|
663.9 |
0.4765 |
689.3 |
0.5360 |
Example \(\PageIndex{2}\)
Example 2: Evaluation of model performance
Problem:
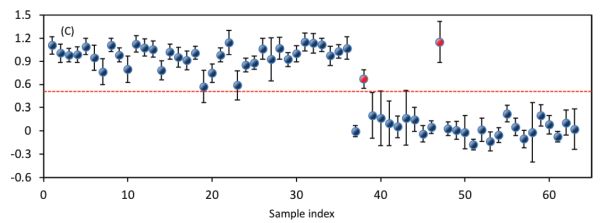
As pigs cannot sweat, it is important to be able to rapidly confirm that conditions in a pig house are not causing them stress. Rectal temperature is the best indicator of heat stress in an animal, but it can be difficult to measure. A pig’s surface temperature, however, can be measured easily using non-contact sensors. Table 2.3.5 shows the performance of two PLSR models used to predict the rectal temperature of pigs by using variables including surface temperature and several environmental conditions. Model 1 is a many-variable model and Model 2 is a simplified model that utilizes an optimized subset of variables. Determine which model is better. The performance of models is presented by R and RMSEs for calibration, cross-validation, and prediction.
Solution
The first step is to check whether R is close to 1 and RMSE to 0. Correlation coefficients range from 0.66 to 0.87 (Table 2.3.5), showing obvious correlation between the predicted rectal temperature and the real rectal temperature. By investigating the RMSEs, it is found that these errors are relatively small (0.25°–0.38°C) compared with the measured range (37.8°–40.2°C). Therefore, both models are useful for predicting the rectal temperature of pigs.
The second step is to check the stability of the established models by evaluating the difference among Rs or RMSEs for calibration, cross-validation, and prediction. For the specific example, although the best correlation coefficient for calibration (RC) and root mean squared error for calibration (RMSEC) were attained for the many-variable model, its performance in cross-validation and prediction was inferior to that of the simplified model. Most importantly, the biggest difference among Rs of the many-variable model was 0.21, while only a tenth of such difference (0.02) was found for the simplified model. A similar trend was also observed for the RMSEs where the maximum differences of 0.05°C and 1.3°C were yielded for the simplified and many-variable models, respectively. These results strongly demonstrate that the simplified model is much more stable than the many-variable model.
| Model | RC | RCV | RP | RMSEC (°C) |
RMSECV (°C) | RMSEP (°C) |
LV |
|---|---|---|---|---|---|---|---|
|
Model 1 |
0.87 |
0.66 |
0.76 |
0.25 |
0.38 |
0.37 |
4 |
|
Model 2 |
0.80 |
0.78 |
0.80 |
0.30 |
0.32 |
0.35 |
2 |
The third step can evaluate the simplicity of the model. In this example, four latent variables were employed to establish the many-variable model while only two were needed for the simplified model. Above all, the simplified model showed better prediction ability, particularly for cross-validation and prediction, with fewer latent variables. Therefore, it is considered as the better model.
Image Credits
Figure 1. Feng, Y. (CC By 4.0). (2020). S-G smoothing of a spectral signal.
Figure 2. Feng, Y. (CC By 4.0). (2020). NIR derivative spectra of bacterial suspensions.
Figure 3. Feng, Y. (CC By 4.0). (2020). SNV processing of vis-NIR spectra of beef samples adulterated with chicken meat.
Figure 4. Feng, Y. (CC By 4.0). (2020). Plot of root mean squared error (RMSE) as a function of number of latent variables (LV) for a PLSR model.
Figure 5. Feng, Y. (CC By 4.0). (2020). Preprocessing of beef spectra.
Figure 7. Feng, Y. (CC By 4.0). (2020). PLS-DA classification model performance in the visible-SWNIR range (400–1000 nm).
Figure 8. Feng, Y. (CC By 4.0). (2020). Example of moving average smoothing of a peach spectrum.
Acknowledgement
Many thanks to Mr. Hai Tao Zhao for his help in preparing this chapter.
References
Bai, X., Wang, Z., Zou, L., & Alsaadi, F. E. (2018). Collaborative fusion estimation over wireless sensor networks for monitoring CO2 concentration in a greenhouse. Information Fusion, 42, 119-126. https://doi.org/10.1016/j.inffus.2017.11.001.
Baietto, M., & Wilson, A. D. (2015). Electronic-nose applications for fruit identification, ripeness and quality grading. Sensors, 15(1), 899-931. https://doi.org/10.3390/s150100899.
Dhanoa, M. S., Lister, S. J., Sanderson, R., & Barnes, R. J. (1994). The link between multiplicative scatter correction (MSC) and standard normal variate (SNV) transformations of NIR spectra. J. Near Infrared Spectroscopy, 2(1), 43-47. https://doi.org/10.1255/jnirs.30.
Feng, Y.-Z., & Sun, D.-W. (2013). Near-infrared hyperspectral imaging in tandem with partial least squares regression and genetic algorithm for non-destructive determination and visualization of Pseudomonas loads in chicken fillets. Talanta, 109, 74-83. https://doi.org/10.1016/j.talanta.2013.01.057.
Feng, Y.-Z., Downey, G., Sun, D.-W., Walsh, D., & Xu, J.-L. (2015). Towards improvement in classification of Escherichia coli, Listeria innocua and their strains in isolated systems based on chemometric analysis of visible and near-infrared spectroscopic data. J. Food Eng., 149, 87-96. https://doi.org/10.1016/j.jfoodeng.2014.09.016.
Feng, Y.-Z., ElMasry, G., Sun, D.-W., Scannell, A. G., Walsh, D., & Morcy, N. (2013). Near-infrared hyperspectral imaging and partial least squares regression for rapid and reagentless determination of Enterobacteriaceae on chicken fillets. Food Chem., 138(2), 1829-1836. https://doi.org/10.1016/j.foodchem.2012.11.040.
Feng, Y.-Z., Zhao, H.-T., Jia, G.-F., Ojukwu, C., & Tan, H.-Q. (2019). Establishment of validated models for non-invasive prediction of rectal temperature of sows using infrared thermography and chemometrics. Int. J. Biometeorol., 63(10), 1405-1415. https://doi.org/10.1007/s00484-019-01758-2.
Friedman, J., Hastie, T., & Tibshirani, R. (2001). The elements of statistical learning. No. 10. New York, NY: Springer.
Ganesh, S. (2010). Multivariate linear regression. In P. Peterson, E. Baker, & B. McGaw (Eds.), International encyclopedia of education (pp. 324-331). Oxford: Elsevier. https://doi.org/10.1016/B978-0-08-044894-7.01350-6.
Gauch, H. G., Hwang, J. T., & Fick, G. W. (2003). Model evaluation by comparison of model-based predictions and measured values. Agron. J., 95(6), 1442-1446. doi.org/10.2134/agronj2003.1442.
Geladi, P., & Kowalski, B. R. (1986). Partial least-squares regression: A tutorial. Anal. Chim. Acta, 185, 1-17. https://doi.org/10.1016/0003-2670(86)80028-9.
Gowen, A. A., O’Donnell, C. P., Cullen, P. J., Downey, G., & Frias, J. M. (2007). Hyperspectral imaging: An emerging process analytical tool for food quality and safety control. Trends Food Sci. Technol., 18(12), 590-598. doi.org/10.1016/j.jpgs.2007.06.001.
Hotelling, H. (1933). Analysis of a complex of statistical variables into principal components. J. Ed. Psychol., 24, 417-441. https://doi.org/10.1037/h0071325.
Klanke, S., & Ritter, H. (2006). A leave-k-out cross-validation scheme for unsupervised kernel regression. In S. Kollias, A. Stafylopatis, W. Duch, & E. Oja (Eds.), Proc. Int. Conf. Artificial Neural Networks. 4132, pp. 427-436. Springer. doi: doi.org/10.1007/11840930_44.
LeCun, Y., Bengio, Y., & Hinton, G. (2015). Deep learning. Nature, 521(7553), 436-444. doi.org/10.1038/nature14539.
Maione, C., & Barbosa, R. M. (2019). Recent applications of multivariate data analysis methods in the authentication of rice and the most analyzed parameters: A review. Critical Rev. Food Sci. Nutrition, 59(12), 1868-1879. https://doi.org/10.1080/10408398.2018.1431763.
Mevik, B.-H., Wehrens, R., & Liland, K. H. (2011). PLS: Partial least squares and principal component regression. R package ver. 2(3). Retrieved from https://cran.r-project.org/web/packages/pls/pls.pdf.
O’Donnell, C. P., Fagan, C., & Cullen, P. J. (2014). Process analytical technology for the food industry. New York, NY: Springer. doi.org/10.1007/978-1-4939-0311-5.
Park, B., & Lu, R. (2015). Hyperspectral imaging technology in food and agriculture. New York, NY: Springer. doi.org/10.1007/978-1-4939-2836-1.
Pham, B. T., Jaafari, A., Prakash, I., & Bui, D. T. (2019). A novel hybrid intelligent model of support vector machines and the MultiBoost ensemble for landslide susceptibility modeling. Bull. Eng. Geol. Environ., 78(4), 2865-2886. doi.org/10.1007/s10064-018-1281-y.
Savitzky, A., & Golay, M. J. (1964). Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem., 36(8), 1627-1639. doi.org/10.1021/ac60214a047.
Townsend, J. T. (1971). Theoretical analysis of an alphabetic confusion matrix. Perception Psychophysics, 9(1), 40-50. doi.org/10.3758/BF03213026.
Zhao, H.-T., Feng, Y.-Z., Chen, W., & Jia, G.-F. (2019). Application of invasive weed optimization and least square support vector machine for prediction of beef adulteration with spoiled beef based on visible near-infrared (Vis-NIR) hyperspectral imaging. Meat Sci., 151, 75-81. https://doi.org/10.1016/j.meatsci.2019.01.010.


