6.3: Deep Fat Frying of Food
- Page ID
- 46859
Ram Yamsaengsung
Department of Chemical Engineering
Faculty of Engineering
Prince of Songkla University
Hat Yai, Thailand
Bandhita Saibandith
Department of Biotechnology
Faculty of Agro-Industry
Kasetsart University
Chatuchak, Bangkok, Thailand
| Key Terms |
| Frying chemistry | Mass transfer | Frying technology |
| Heat transfer | Mass and material balance | Industrial continuous frying systems |
| Heat balance | Product drying rate | Vacuum frying systems |
Variables
Introduction
This chapter introduces the basic principles of frying and its relevance to the food industry. To illustrate its importance, various fried products from around the world are described, and the mechanisms, equipment, and chemistry of the frying process are discussed. The pros and cons of frying food are presented in the context of texture, appearance, taste, and acceptability.
Frying is a highly popular method of cooking and has been used for thousands of years. A few examples from around the world include noodles, egg rolls, and crispy taros in China; tempuras (battered fried meats and vegetables) in Japan; fish and chips in the United Kingdom; and fried pork legs in Germany. In Latin countries and Tex-Mex restaurants, fried foods include tortilla-based products, such as tacos, nachos, and quesadillas. Examples of other popular fried foods include French fries, onion rings, and fried chicken, along with fried desserts such as doughnuts and battered, fried candy bars.
Traditionally, there are two major types of fried foods: (1) deep-fat fried (deep fried), such as potato chips, French fries, and battered fried chicken; and (2) pan fried, such as pancakes, eggs, and stir-fried dishes. This chapter focuses on atmospheric and vacuum deep-fat frying systems.
Outcomes
After reading this chapter, you should be able to:
- • Describe various types of frying technology
- • Describe basic frying chemistry and the heat and mass transfer mechanisms that are involved in the manufacture of different types of fried products
- • Explain the advantages and disadvantages of the frying process
- • Analyze the frying process using fundamental equations and calculate rate of water removal and amount of heat required during frying
Concepts
Frying Technology
Frying is defined as the process of cooking and drying through contact with hot oil. It involves simultaneous heat and mass transfer. Frying technology is important to many sectors of the food industry from suppliers of oils and ingredients; to fast-food outlets and restaurants; to industrial producers of fully fried, par-fried, and snack food products; and finally to manufacturers of frying equipment. The amount of fried food and oil used at both the industrial and commercial levels is massive.
Deep-Fat Frying (Deep Frying)
The process of immersing food partially or completely in oil during part or all of the cooking period at atmospheric pressure (760 mm Hg or 101.3 kPa absolute) is called deep-fat frying or deep frying. The food is completely surrounded by the oil, which is a very efficient heat-transfer medium. In addition to cooking the food, frying oil produces a crispy texture in food such as potato chips, French fries, and battered fried chicken (Moreira et al., 1999). The resulting product is usually golden brown in color with an oil content ranging from 8 to 25%.
A typical deep-fat fryer consists of a chamber into which heated oil and a food product are placed. The speed and efficiency of the frying process depend on the temperature and the overall quality of the oil, in terms of degradation of triglycerides and changes in thermal and physical properties such as color and viscosity (Moreira et al., 1999). The frying temperature is usually between 160° and 190°C. Cooking oil (such as sunflower oil, canola oil, soybean oil, corn oil, peanut oil, and olive oil) not only acts as the heat transfer medium, but it also enters into the product, providing flavor; Table 6.3.1 lists the oil content of commonly deep-fat fried products.
In addition to frying at atmospheric pressure, food products can also be fried under a vacuum, where the pressure is reduced to about 60 mm Hg (8 kPa absolute). At this lower pressure, the boiling point of water is decreased to 41°C allowing for the frying oil temperature to be reduced to 90°–110°C. As a result, heat-sensitive products, such as fruits with a high sugar content (e.g., bananas, apples, jackfruits, durians, and pineapples) can be fried to a crisp. Furthermore, the fried products are able to maintain a fresh color and intense flavor, while the frying oil will have a longer life because of less contact with atmospheric oxygen.
| Product | Oil Content (%) |
|---|---|
|
Potato chips |
33–38 |
|
Tortilla chips |
23–30 |
|
Expanded snack products |
20–40 |
|
Roasted nuts |
5–6 |
|
French fries |
10–15 |
|
Doughnuts |
20–25 |
|
Frozen foods |
10–15 |
Chemistry of Frying
Sources of Oil Used in Frying
Oil seed crops are planted throughout the world to produce cooking oil. The seeds are washed and crushed before oil is removed using an extraction process. The oil is then refined to remove any unwanted taste, smell, color, or impurities. Some oils, such as virgin olive oil, walnut oil, and grapeseed oil, are pressed straight from the seed or fruit without further refining (EUFIC, 2014). Some other sources of frying oil include sunflower, canola, palm, and soybean.
Most vegetable oils are liquid at room temperature. When oils are heated, unsaturated fatty acids, which are the building blocks of triglycerides, are degraded. Monounsaturated-rich oils, such as olive oil or peanut oil, are more stable and can be re-used much more than polyunsaturated-rich oils like corn oil or soybean oil. For this reason, when deep-frying foods, it is important not to overheat the oil and to change it frequently.
Chemical Reactions
Many chemical reactions, including hydrolysis, isomerization, and pyrolysis, take place during frying and affect the quality and storage time of the oil. Several of these reactions lead to spoilage of the oil.
Hydrolysis is a chemical reaction in which a water molecule is inserted across a covalent bond and breaks the bond. Hydrolysis is the major chemical reaction that occurs during frying. As the food product is heated, water in the food evaporates and the water vapor diffuses into the oil. The water molecules cause hydrolysis in the oil, resulting in the formation of free fatty acids, reduction of the smoke point of the oil, and unpleasant flavors in both the oil and the food. The smoke point, or the burning point, of an oil or fat is the temperature at which it begins to produce a continuous bluish smoke that becomes clearly visible (AOCS, 2017). Baking powder also promotes hydrolysis of the oil (Moreira et al., 1999). Table 6.3.2 lists the smoke points of some common oils used in frying. For high temperature cooking (160–190°C), an oil with a low smoke point, such as unrefined sunflower oil and unrefined corn oil, may not be suitable.
| Cooking Oils and Fats | Smoke Point °C | Smoke Point °F | Cooking Oils and Fats | Smoke Point °C | Smoke Point °F |
|---|---|---|---|---|---|
|
Unrefined sunflower oil |
107°C |
225°F |
Grapeseed oil |
216°C |
420°F |
|
Unrefined corn oil |
160°C |
320°F |
Virgin olive oil |
216°C |
420°F |
|
Butter |
177°C |
350°F |
Sunflower oil |
227°C |
440°F |
|
Coconut oil |
177°C |
350°F |
Refined corn oil |
232°C |
450°F |
|
Vegetable shortening |
182°C |
360°F |
Palm oil |
232°C |
450°F |
|
Lard |
182°C |
370°F |
Extra light olive oil |
242°C |
468°F |
|
Refined canola oil |
204°C |
400°F |
Rice bran oil |
254°C |
490°F |
|
Sesame oil |
210°C |
410°F |
Avocado oil |
271°C |
520°F |
Isomerization (polymerization) is the process by which one molecule is transformed into another molecule that has exactly the same atoms but arranged differently. Isomerization occurs rapidly during standby and frying periods. The bonds in the triglycerides are rearranged, making the oil more unstable and more sensitive to oxidation.
Pyrolysis results in the extensive breakdown of the chemical structure of the oil resulting in the formation of compounds of lower molecular weight.
Fried foods may absorb many oxidative products, such as hydro-peroxide and aldehydes, that are produced during frying (Sikorski & Kolakowska, 2002), thus affecting the quality of oil.
Repeated frying (using the same oil several times) increases the viscosity and darkens the color of the cooking oil. If the physico-chemical properties of cooking oil deteriorate, the oil must be discarded because it can prove to be harmful for human consumption (Goswami et al., 2015; Rani et al., 2010; Choe et al., 2007). Antioxidants, such as Vitamin E, added during frying are extremely effective in decreasing the rate of lipid oxidation, while enzymes such as superoxide dismutase, catalase, and peroxidase are also beneficial. Nonetheless, Vitamin E effectiveness decreases with increasing temperature (Goswami et al., 2015).
Heat and Mass Transfer Processes During Frying
The frying process, whether atmospheric or vacuum frying, is quite complicated involving coupled heat and mass transfer through a porous medium (the food), crust formation, and product shrinkage and expansion. These mechanisms all contribute to the difficulties in predicting physical and structural appearance of the final product. Thus, an understanding of the frying mechanism and the heat and mass transport phenomena is useful for food processors in order to produce and develop new fried and vacuum fried snack foods to meet the demands of consumers.
Heat Transfer
During the frying process, both heat and mass transfer take place, with water leaving and oil entering the product (Figure 6.3.1). The heat transfer processes include radiation from the heat source to the fryer, conduction from the fryer outer wall to the inner surface, and from inner surface to oil. Once the oil is heated, heat energy is transferred by convection to the surface of the product. Due to the high temperature of frying (160–190°C), the convective heat transfer coefficient is much higher than air-drying processes. Finally, heat is conducted from the hotter surface to the colder center of the product, thus increasing its temperature.

Heat transfer during the frying process can be described using the three following simplifying assumptions (Equations 6.3.1–6.3.3) relating to convection, conduction, and sensible heat.
The first assumption is that heat is transferred from the oil to the product surface via convection:
\[ q=h\Delta T = hA(T_{s}-T_{\infty}) \]
where q = heat flux (J s−1m−2 or W m−2) (due to convection, in this case)
h = convective heat transfer coefficient (W m−2 °C −1)
A = surface area of product (m2)
∆T = difference in temperature (°C) between the product surface temperature and the oil temperature = Ts – T∞
Ts = product surface temperature (°C)
T∞ = oil temperature (°C)
Table 6.3.3 lists ranges of values of the convective heat transfer coefficient (h) for several processes and media. Forced convection increases the heat transfer coefficient dramatically compared to free convection. At the same time, liquids have a much greater h value than gases, while a convection process with phase change can create a heat transfer coefficient as high as 2,500–100,000 W m−2. Krokida et al. (2002) provide a good compilation of literature data on convective heat transfer coefficients in food processing operations and Alvis et al. (2009) is a good source for values of the coefficient in frying operations.
The second assumption is that heat is transferred from the product surface internally via conduction:
\[ q=hA\frac{\Delta T}{\Delta x} = kA\frac{(T_{1}-T_{2})}{\Delta x} \]
| Process | h (W m−2 K−1) |
|---|---|
| Free convection: | |
|
Gases (e.g., air) |
2–20 |
|
Liquids (e.g., water, oil) |
50–1000 |
| Forced convection: | |
|
Gases (e.g., air) |
25–300 |
|
Liquids (e.g., water, oil) |
100–40,000 |
| Convection with phase change: | |
|
Boiling or condensation |
2,500–100,000 |
where q = heat flux (J s−1m−2) or (W m−2) (due to conduction in this case)
k = thermal conductivity (W m−1 °C −1)
A = surface area of product (m2)
∆T = T1 – T2 = difference in temperature between the inner and outer surface of the product (°C)
∆x = thickness of product (m)
The third assumption is that the heat from the oil is also used as sensible heat (change in the temperature of the product without a change in phase) to increase the product temperature toward the oil temperature:
\[ Q=\Delta H = \dot{m}C_{p} \Delta T= \dot{m}C_{p}(T_{1}-T_{2}) \]
where Q = sensible heat (J s−1)
∆H = change in enthalpy (J)
\(\dot{m}\) = mass flow rate (kg s−1)
Cp = specific heat (kJ kg−1 °C−1)
∆T = T1 – T2 = change in temperature of the material without undergoing a phase change (°C)
Table 6.3.4 gives the specific heat of water, vegetable oil, and common materials. As shown, the specific heat of vegetable oil is less than half that of liquid water, indicating that much less energy is needed to raise the temperature of the same amount of material by 1°C.
| Material | Specific Heat (Cp) (kJ kg−1 °C−1) |
|---|---|
|
Liquid water |
4.18 |
|
Solid water (ice) |
2.11 |
|
Water vapor |
2.00 |
|
Vegetable oil |
2.00 |
|
Dry air |
1.01 |
Sensible heat from the oil increases the water temperature to its boiling point. The release of heat energy at the boiling point is known as the latent heat of vaporization, or the heat required to evaporate the water or change its phase from liquid to gas. The latent heat of vaporization cools the product region during evaporation, keeping the product temperature near the boiling point (until most of the water has been removed).
Heat Balance
The simplified heat balance equation is:
\[ \rho C_{p}\frac{dT}{dt}-div[k\nabla T] = Q_{\text{heatsource}}+h(T-T_{\infty}) \]
where ρ = density of product (kg m−3)
Cp = heat capacity of product (J kg−1 °C−1)
div[k∇(T)] = conduction term = \(\frac{\partial}{\partial x}(k\frac{\partial T}{\partial x})+\frac{\partial}{\partial y}(k\frac{\partial T}{\partial y})+\frac{\partial}{\partial z}(k\frac{\partial T}{\partial z})\)
x = direction x (m)
y = direction y (m)
z = direction z (m)
k = thermal conductivity (W m−1 °C−1)
Qheatsource = latent heat of evaporation term (J s−1m−2)
h = convective heat transfer coefficient (W m−2 °C−1)
T∞ = oil temperature at time t (°C)
T = product temperature at time t (°C)
t = time (s)
The simplified heat balance equation (Equation 6.3.4), consists of the heat accumulation term [ρCp(dT/dt)], the conduction term div[k∇(T)], the heat source term (Qheatsource) denoting the latent heat of vaporization, and the convection term, h(Toil – T), at the boundary surface, respectively. The heat accumulation term represents the change in the enthalpy of the system as a function of time. This change accounts for the heating of the product (change in enthalpy) and the transfer of the heat from the heated product toward evaporating the water vapor from the product. The conduction term accounts for the transfer of the heat from the product surface toward the center of the material, while the convection term accounts for the transfer of heat from the oil to the product surface and is dependent on the heat transfer coefficient of the cooking oil (Yamsaengsung et al., 2008).
Mass Transfer
The mass transfer processes during frying include (Figure 6.3.1):
- 1. As the hot oil heats the product by conduction, the heat evaporates the water in the product when it reaches the water boiling temperature (Farkas et al., 1996).
- 2. As the water turns into vapor, it diffuses within the product and moves out of the product by convection.
- 3. Oil is driven into the product via capillary pressure (which is the pressure difference between two immiscible fluids in a thin tube), resulting from the interactions of forces between the fluids and the solid walls of the tube. Capillary pressure can serve as both an opposing force and a driving force for fluid transport (Moreira and Barrufet, 1998).
- 4. The final product is comprised of solids, water, air, and oil. In general, the product becomes more hygroscopic, i.e., readily attracts water from its surrounding, as frying proceeds. French fries are an excellent example of a product with a crispy surface or crust and a soft inner portion called crumb. In brief, after a specific time, the surface of the product becomes crispy, while the internal part of the product may retain a certain amount of moisture, leaving it with a softer texture.
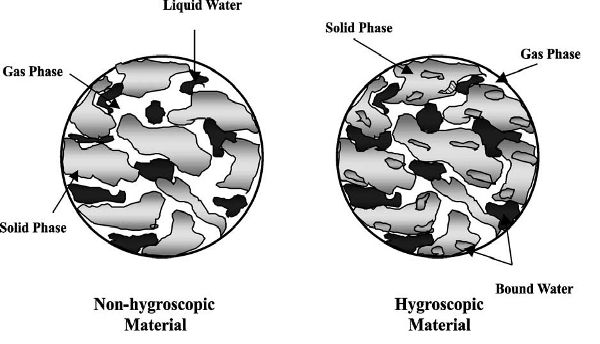
Figure 6.3.2 depicts a typical non-hygroscopic material and a hygroscopic material (Figura and Teixeira, 2007). Each material consists of all three phases: gas, liquid water, and solid. One major difference is that in a hygroscopic material there is bound water. Bound water is defined as water that is bonded strongly to the inner surface of the pores of the materials (Yamsaengsung and Moreira, 2002) and very difficult to remove. In contrast, free water can be removed through capillary diffusion (Moreira et al., 1999) and convection flow from a pressure gradient. The bound water requires a longer drying and frying time to be removed. While more heat energy is required to remove this bound water, its removal leads to shrinkage of the material. Drying can also lead to shrinkage of the material, but frying can lead to additional puffing and expansion of the structure as the water vapor and gas expand during the later stages of the frying process (Yamsaengsung and Moreira, 2002).
Product Drying Rate
The percent moisture content of a food material can be expressed as wet basis (% w.b.) or dry basis (% d.b.) by mass. Percentage wet basis is commonly used in commercial applications while percentage dry basis is used in research reports.
The % w.b. is defined as:
\[ \%\ w.b.=(\frac{\text{water content (kg)}}{\text{total weight of product (kg)}}) \cdot100 \]
The % d.b. is defined as:
\[ \%\ d.b.=(\frac{\text{kg of water}}{\text{kg of dried food}}) \cdot100 \]
The drying rate of the product during the frying process is divided into constant and falling rate periods. During the constant rate period, water removal is fairly constant. During the falling rate period, the rate of water removal is drastically reduced. Each period is characterized by an averaged set of heat and mass transport parameters (Yamsaengsung, 2014). The moisture ratio (MR) is defined as:
\[ MR = \frac{MC_{t}-MC_{e}}{MC_{o}-MC_{e}} \]
where MR = moisture ratio
MCt = moisture content at frying time t (decimal d.b. or w.b.)
MCe = equilibrium moisture content; the moisture content of the product under equilibrium conditions at constant temperature and relative humidity (d.b. or w.b.)
MC0 = moisture content at start of frying, time = 0 (d.b. or w.b.)
Figure 6.3.3 illustrates the constant rate and the falling rate periods of the MR during the frying process.
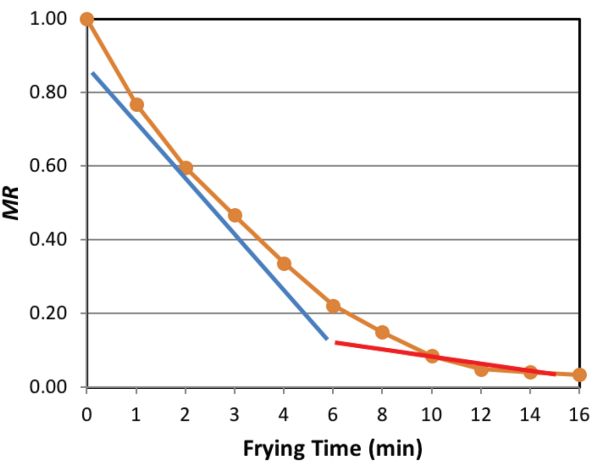
During the constant rate period, free water is removed as vapor via evaporation and diffusion from the product. Changes in the product surface as the crust forms are also taking place during this period. Typically, for crispy foods, the moisture content should be less than 5% w.b. During the falling rate period, a distinct crust region has been developed and bound water is being removed via vapor diffusion. The rate of oil absorption is proportional to the rate of moisture loss during the constant rate period, but is limited by the presence of the crust during the falling rate period. The development of crust and the increase in pressure inside the structure as the gas vapor expands with continuous heat absorption help to limit oil absorption, while causing the pores of the product to expand and the entire product to increase its thickness. This expansion is called puffing (Moreira et al., 1999).
In terms of mass transfer, the diffusion equation (Equation 6.3.8) may be written to account for the convective flow of liquid and vapor as (Moreira et al., 1999):
\[ \frac{dc}{dt}-div[D\cdot \nabla(c)]=\dot{V} \]
where \(\frac{dc}{dt}\) = change in concentration of component (liquid, vapor, or oil) (kg mol m−2 s−1)
div[D·∇(c)] = convective flow = \(\frac{\partial}{\partial x}(k\frac{\partial T}{\partial x})+\frac{\partial}{\partial y}(k\frac{\partial T}{\partial y})+\frac{\partial}{\partial z}(k\frac{\partial T}{\partial z})\)
D = diffusion coefficient (m−2 s−1)
c = concentration of component (liquid, vapor, or oil) (kg mol m−3)
\(\dot{V}\)= rate of convective flow of liquid (kg mol m−2 s−1)
When applied to each component, i.e., liquid, vapor, or oil, Equation 6.3.8 is used to quantify the removal of liquid water and vapor from the product and the absorption of oil by the product during the frying process, i.e., as a function of time. The rate of water removal is estimated using the diffusion coefficient, while the change in the concentration of the component (liquid, vapor, or oil) is estimated using experimental data as a function of frying time (Yamsaengsung, et. al., 2008).
The heat and mass transfer equations allow calculation of the energy consumption, the heat required for heating of the cooking oil and removal of water from the product during the frying process, the amount of water that is being removed during frying, and, in many cases, the amount of product that would be obtained at the end of the frying period.
Material (Mass) Balance
Equations 6.3.4 and 6.3.8 describe heat and mass transfer during frying in three dimensions. Solving them requires advanced numerical methods, which are beyond the scope of this chapter. This section presents a model using simplified material balance (mass balance) equations, which accounts for the change in mass of each component during the process.
Equation 6.3.9 states the concept of the material, or mass, balance in words:
\[ \{ \text{accumulation within the system} \}=\{\text{input through system boundaries} \} - \{\text{output through system boundaries} \} + \{\text{generation within the system} \} - \{\text{consumption within the system} \} \]
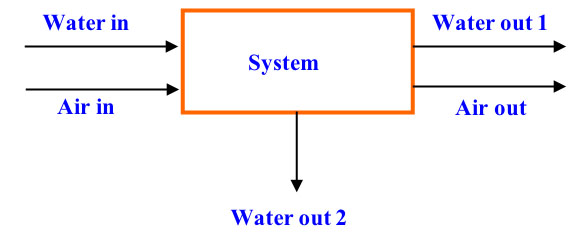
Accumulation refers to a change in mass (plus or minus) within the system with respect to time, whereas the input and output through the system boundaries refers to inputs and outputs of the system (Himmelblau, 1996). If considered over a time period for which the balance applies, Equation 6.3.9 is a differential equation (consider, for example, the mass balance of water in Figure 6.3.4). When formulated for an instant of time, Equation 6.3.9 becomes a differential equation:
\[ \frac{dm_{H_{2}O,within\ system}}{dt}=\dot{m}_{H_{2}O,in} - \dot{m}_{H_{2}O,out1} - \dot{m}_{H_{2}O,out2} \]
where mH2O is the mass of water and \(\dot{m}\)H2O is the mass flow rate of water (mass/time, kg/s). When evaluating a process that is under equilibrium, or steady-state, condition, the values of the variables within the system do not change with time, and the accumulation (change in mass within the system with respect to time) term in Equations 6.3.9 and 6.3.10 is zero.
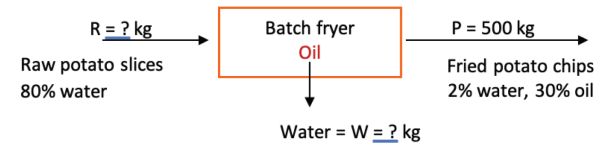
To illustrate application of the mass balance, consider a frying operation to make potato chips (which are fried potato slices). For this example, 4 kg of peeled raw potato slices containing 83% water enter a fryer to make chips with 2% water and 30% oil. How many kg of water are evaporated from the product leaving the fryer, and how many kg of potato chips are produced in the process? The process is at steady state conditions.
The system is the fryer, and no accumulation, generation, or consumption occurs, since the process is steady state. Also, assume potatoes are made up of water and solids. The next step is to write the mass balance equations, total and for each component (% solids, % water), and solve for the unknowns.
The total mass balance of potato slices is:
in = out, as the time-dependent terms in Equation 6.3.10 are zero
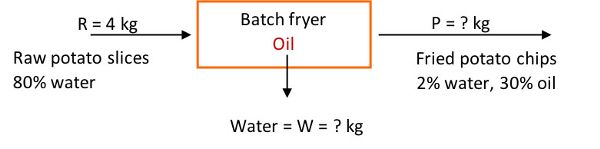
R + oil (absorbed from fryer) = W + P
The total material entering the fryer is given as 4 kg peeled raw potato slices. Substituting R = 4 kg in the total mass balance, yields one equation with two unknowns:
4 kg + oil (absorbed from fryer) = W + P
Hence, a second equation is needed (basic material balances principle). The potatoes are composed of water and solids, hence, the terms in the total mass balance equation can be multiplied by the respective component percentages. The percent solids balance is:
4 kg (1 – 0.83) + 0 = W(0) + P(1 – 0.32)
0.68 = 0.68 P
P = 1 kg of potato chips produced
Percent water balance is:
4 kg (0.83) + 0 = W(1) + P(0.02)
3.32 = W + 0.02 P
3.32 = W + (0.02) 1 kg = W + 0.02
W = 3.3 kg of water removed
Percent oil balance:
4 kg (0) + oil = 3.3 kg(0) + 1 kg(0.3)
Thus, the mass of oil absorbed by the potatoes during frying is 0.3 kg.
The total material balance is 4 kg + 0.3 kg = 3.3 kg + 1 kg, or 4.3 = 4.3, which confirms the conservation of mass law.
Applications
In order to design and construct a productive and cost-effective frying system, product properties and characteristics, including size, shape, thickness, thermal conductivity, specific heat capacity, composition, and desired product attributes, such as color, texture (hardness, crispiness), smell, and flavor, all play a role and affect the frying time and temperature. Using equations for mass balance and heat transfer, the rate of water removal and a drying curve can be developed which can be used to predict the moisture loss and the product weight, which, in turn, affects the frying time and production capacity.
Industrial Continuous Deep-Fat Frying Systems
A typical continuous frying system consists of a fryer, a heat exchanger, an oil tank with a cooling system, a control panel, and a filter. Another common type of frying system consists of a combustor, an oil heat exchanger, and a fryer. In the combustor, a gas burner burns natural gas with fresh air and foul gas (vapors from the fryer) to produce combustion gases that flow through a heat exchanger to heat the frying oil that is re-circulated through the fryer. In many cases, exhaust gas recirculation is used to increase turbulence, provide combustor surface cooling, and reduce emissions. To reduce emissions and smells, vapors generated from the frying process are directed from the fryer to the combustor where they are incinerated (Wu et al., 2013).
Table 6.3.5 provides examples of mechanical specifications of some continuous frying systems and their throughputs, while Table 6.3.6 gives pricing and frying time of some systems.
| Model | Dimensions (mm) |
Effective Frying Space, length × width × height (mm) | Hp | Energy Consumption (kWh) | Edible Oil Capacity (L) | Production Capacity | |||
|---|---|---|---|---|---|---|---|---|---|
| length | width | height | Peanuts | Snacks | |||||
|
FRYIN-302-E |
3450 |
2350 |
1950 |
2600 × 820 × 700 |
3 |
232.44 |
440 |
480 kg/hr |
300 kg/hr |
|
FRYIN-402-E |
4950 |
2350 |
1950 |
4100 × 820 × 700 |
5 |
348.67 |
650 |
650 kg/hr |
550 kg/hr |
|
FRYIN-602-E |
6450 |
2450 |
2070 |
5890 × 820 × 700 |
7.5 |
464.89 |
850 |
||
Modified from https://www.tsunghsing.com.tw/en/product/oil_fryer-fryin_series.html
Vacuum Frying Systems
The vacuum frying process, first developed in the 1960s and early 1970s, provides several benefits compared to the traditional (atmospheric) frying process. It is now widely used to process fruits in Asian countries. The principle behind vacuum frying is that using reduced pressure (below 101.3 kPa), the boiling point of water can be reduced from 100°C to as low as 45°C and the cooking oil temperature can also be reduced to less than 100°C (compared to atmospheric frying at 170°–190°C). As a result, products with high sugar content, such as ripened fruits, can be fried without burning and caramelization. Common methods to improve vacuum-frying of fruits include immersion in high sugar solutions and osmotic dehydration (Fito, 1994; Shyu and Hwang, 2001).
| Machine Type | Products | Fuel Source/Power Consumption | Capacity (kg/hr) |
Frying Time (min.) |
Cost, US$ |
|---|---|---|---|---|---|
|
Automatic continuous fried nuts processing line |
nuts, almond, cashew, peanuts, etc. |
diesel, LPG, gas, biofuel |
N/A |
N/A |
$143,145 |
|
Automatic snacks frying machine |
chips, meat, chicken, peanut |
electric/10 kW |
100–1,000 |
N/A |
$14,314 |
|
Continuous banana chips fryer machine |
chips, biscuit, donut, French fries, potato chips, banana chips, snacks |
electric/25 kW |
100–500 |
2–20 |
$25,766 |
|
Snack food fryer |
snack foods |
electric/25 kW |
100–500 |
1–10 |
$143,145 |
Modified from https://www.gracefoodmachinery.com/continuous-fryer-systems.html
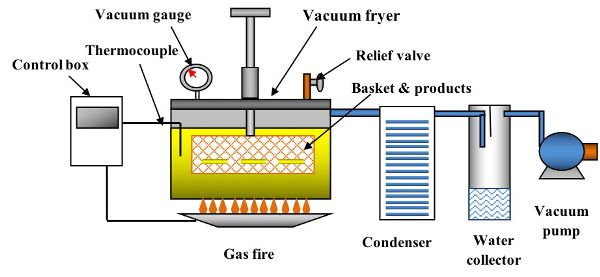
Figure 6.3.6 shows a schematic of a vacuum fryer (Yamsaengsung, 2014). In addition to the features shown in Figure 6.3.6, a vacuum fryer must have a centrifuge to remove the oil content from the surface before the vacuum is broken. Table 6.3.7 provides a comparison of process operating conditions and applications for traditional and vacuum frying systems. The main components in the vacuum frying process are the vacuum fryer (8–10 mm thick wall and fryer cap), the condenser (for condensing water vapor), the water collector, and the vacuum pump (either rotary or liquid water ring type). However, the main drawbacks of vacuum frying are the high cost involved in purchasing the equipment and the more complicated process management. With the addition of a vacuum pump, a water condensing system, and much thicker fryer wall (8–10 mm vs. 1–2 mm), the cost of the vacuum fryer can be double the cost of an atmospheric fryer.
The benefits of vacuum frying include the ability to:
- • fry high sugar content products such as fresh fruits;
- • maintain original color, while adding intense flavor to the final product;
| Conditions/Attributes | Atmospheric Frying | Vacuum Frying |
|---|---|---|
|
Temperature |
160°–190°C |
90°–140°C |
|
Pressure (absolute) |
101.3 kPa |
3.115 kPa |
|
Convective heat transfer coefficient (h) |
−2 K−1 (80-120°C)[b] −2 K−1 (200-300°C)[b] |
217–258 W m−2 K−1 (120°–140°C)[c] 700–1600 W m−2 K−1 (140°C)[d] |
|
Oil absorption |
25–40% w.b. |
1–10% w.b. |
|
Oil usage life |
susceptible to lipid oxidation |
minimal lipid oxidation longer usage life |
|
High sugar content foods |
not possible |
possible |
|
Major composition |
high starch/ high protein |
high starch high protein high sugar |
|
Taste/texture |
bland to salty/crispy |
intense flavor/crispy |
|
Color |
intensity of color decreases |
intensity of color is maintained |
|
Investment cost |
low |
high |
[a] Yamsaengsung (2014); [b] Farinu and Baik (2007) at 160°–190°C; [c] Pandey and Moreira (2012) at 120°–140°C; [d] Mir-Bel et al. (2012) at 140°C.
- • reduce the amount of oil absorbed into the final product to as low as 1–3% depending on the machine (Garayo & Moreira, 2002); and
- • extend the life of cooking oil by reducing its exposure to oxygen (lipid oxidation) and using a lower cooking oil temperature.
Moreover, even though Garayo and Moreira (2002) found that potato chips fried under vacuum conditions (3.115 kPa and 144°C) had more volume shrinkage, their texture was slightly softer and they were lighter in color than potato chips fried under atmospheric conditions (165°C). Yamsaengung and Rungsee (2003) also found that, compared to atmospheric frying, vacuum fried potato chips retained a lighter color and had a more intense flavor.
Examples
Example \(\PageIndex{1}\)
Example 1: Material balances
Problem:
Determine how many kg of raw potato slices containing 80% water must enter a batch fryer to make 500 kg of potato chips (fried potato slices) with 2% water and 30% oil. Also calculate how many kg of water are evaporated and leave the fryer. The process is at steady state conditions.
Solution
Draw a schematic of the problem, enter the given data and identify the unknowns. Then, write down the material balance equations and solve for the unknowns.

The system is the fryer, and no accumulation, generation, or consumption occurs, that is, it is at steady state. Also assume potatoes are made up of water and solids.
The total material balance in the fryer is:
in = out
R + oil (in fryer) = W + P
R + oil = W + 500 kg
We have one equation and two unknowns, so we need another equation.
Percent solids balance:
R(1 – 0.80) + 0 = W(0) + 500 kg(1 – 0.32)
R = 1700 kg
R = 1700 kg of raw potato slices containing 80% water are required
Percent water balance is:
1700 kg(0.80) + 0 = W(1) + 500 kg(0.02)
1360 = W + 10
W = 1350 kg of water removed from potato slices in the frying process
Finally, determine the amount of oil in the fried chips by conducting a percent oil balance:
1700 kg(0) + oil = 1350 kg(0) + 500 kg(0.3)
oil = 150 kg
Total material balance:
1700 kg + 150 kg = 1350 kg + 500 kg
This example illustrates the use of material balances using food initial and final composition data to calculate the amount of raw material entering the fryer to manufacture a product with specific composition characteristics.
Example \(\PageIndex{2}\)
Example 2: Moisture content of fried chips
Problem:
During a batch frying process, the weight of 50 kg of raw, fresh peeled potato slices decreases to 15 kg after frying. Each fried chip contains 30% oil content. If the initial moisture content of the fresh peeled potato is 80% (w.b), determine the final moisture content (% w.b.) of the fried chips.
Solution
Draw a schematic of the problem, enter the given data and identify the unknowns. Then, write down the material balance equations and solve for the unknown moisture content of the fried chips, using the definition of percent wet basis.
The system is the fryer, and no accumulation, generation, or consumption occurs (steady state). Also assume potatoes are made up of water and solids.
The total material balance in the fryer is:
in = out
R + oil absorbed = W + P
From the problem statement, mass of P = 15 kg with 30% oil.
Using percent oil content, calculate how much oil (in kg) the chips contain:
0.30 × 15 kg = 4.5 kg of oil in fried chips
To figure the percent solids balance, note that in material balance applications in food engineering, the dry matter is constant. Hence, solids in = solids out.
From the raw materials with 80% water (and 20% solids), the dry matter (% solids) is:
50 kg × 0.2 = 10 kg
Calculate how much water (in kg) is in the chips:
chips = water + dry matter + oil
15 kg = kg H2O + 10 kg + 4.5 kg
kg H2O = 15 kg – 10 kg – 4.5 kg = 0.05 kg
Then, on a wet basis, the moisture content of the chips is (from Equation 6.3.5):
\( \%\ w.b. = \frac{\text{kg of water}}{\text{total of weight of product}} \times 100= \frac{0.05\ kg}{15\ kg}\times100=0.333\% \)
This example shows how the final moisture content of the fried product can be calculated. Its importance lies in the effect of moisture on the crispiness of fried foods. Typically, for crispy snacks, the moisture content should be less than 5% w.b., so this fried product is considered crispy.
Example \(\PageIndex{3}\)
Example 3: Drying curve
Problem:
The following data represent the change in weight of vacuum fried bananas (70% w.b. moisture content) as a function of frying time. Also assume the moisture content in % d.b. at equilibrium (at the end of frying) is 0.02 kg water/kg dry matter. Neglect the weight of the oil absorbed (% oil content = 0.0%) and plot the drying curve as a function of the frying time (moisture ratio vs. time).
| Time (min) |
Weight (kg) |
Solids (kg) |
H2O (kg) |
|---|---|---|---|
|
0 |
10 |
3 |
7 |
|
1 |
8.4 |
3 |
5.4 |
|
2 |
7.2 |
3 |
4.2 |
|
3 |
6.3 |
3 |
3.3 |
|
4 |
5.4 |
3 |
2.4 |
|
6 |
4.6 |
3 |
1.6 |
|
8 |
4.1 |
3 |
1.1 |
|
10 |
3.65 |
3 |
0.65 |
|
12 |
3.4 |
3 |
0.4 |
|
14 |
3.35 |
3 |
0.35 |
|
16 |
3.3 |
3 |
0.3 |
Solution
Calculate moisture ratio using Equations 6.3.6 and 6.3.7:
\( \%\ d.b. = \frac{\text{kg of water}}{\text{total of weight of product}} \cdot 100 \) (Equation \(\PageIndex{6}\))
\( MR = \frac{MC_{t}-MC_{e}}{MC_{o}-MC_{e}} \)
For the banana with 70% w.b. moisture, the percent solids content is 1 – 0.7 = 0.3 or 30%. For an initial weight of 10 kg, the solids content is 0.3 × 10 kg = 3 kg (a constant throughout the process).
Determine moisture content in % dry basis using Equation 6.3.6 at each time t:
% d.b. = (total weight – weight of solids)/(weight of solids)
For example,
At t = 0 min MC0 (t=0) = (10 kg – 3 kg)/(3 kg) = 2.33
At t = 1 min MC1 (t=1) = (8.4 kg – 3 kg)/(3 kg) = 1.80
At t = 2 min MC2 (t=2) = (7.2 kg – 3 kg)/(3 kg) = 1.40
Repeat the procedure for all times.
Next, determine MR using Equation 6.3.7. For example,
MRt = (MCt – MCe)/(MCo – MCe)
At t = 0 min MR0 = (2.33 – 0.02)/(2.33 – 0.02) = 1.00
At t = 1 min MR1 = (1.80 – 0.02)/(2.33 – 0.02) = 0.77
At t = 2 min MR2 = (1.40 – 0.02)/(2.33 – 0.02) = 0.60
Repeat the procedure for all times using table below.
| Time (min) |
Weight (kg) | Solids (kg) |
H2O (kg) |
MC (d.b.) |
MR |
|---|---|---|---|---|---|
|
0 |
10 |
3 |
7 |
2.33 |
1.00 |
|
1 |
8.4 |
3 |
5.4 |
1.80 |
0.77 |
|
2 |
7.2 |
3 |
4.2 |
1.40 |
0.60 |
|
3 |
6.3 |
3 |
3.3 |
1.10 |
0.47 |
|
4 |
5.4 |
3 |
2.4 |
0.80 |
0.34 |
|
6 |
4.6 |
3 |
1.6 |
0.53 |
0.22 |
|
8 |
4.1 |
3 |
1.1 |
0.37 |
0.15 |
|
10 |
3.65 |
3 |
0.65 |
0.22 |
0.09 |
|
12 |
3.4 |
3 |
0.4 |
0.13 |
0.05 |
|
14 |
3.35 |
3 |
0.35 |
0.12 |
0.04 |
|
16 |
3.3 |
3 |
0.3 |
0.10 |
0.03 |

Example \(\PageIndex{4}\)
Example 4: Production throughput of a continuous fryer
Problem:
At a potato chip factory, 1,000 kg of potatoes are fed into a continuous vacuum fryer per hour.
- (a) Assuming the initial moisture content of peeled potatoes is 80% (w.b.) and the final moisture content is 2% (w.b.), how much water is removed per hour?
- (b) How much (in kg) of oil is added to the potato chips per hour? Potato chips have 2% w.b. moisture content and 30% oil.
- (c) How many bags can be produced in one day if each bag contains 50 g of potato chips and the factory operates for 8 hours per day?
Solution
Draw a schematic of the problem, enter the given data and identify the unknowns. Then, write down the material balance equations and solve for the unknowns. Neglect oil content in product. This is a continuous process (material/time).
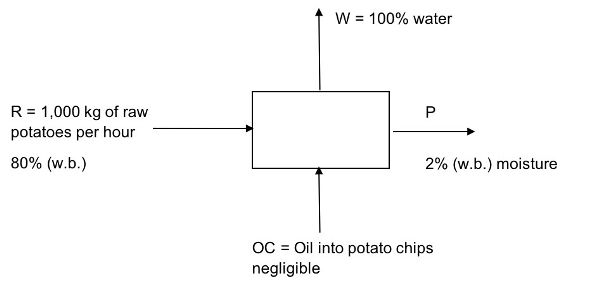
- (a) Determine the amount of water removed from the raw potatoes, R, per hour.
Water in initial product:
1,000 kg/hr × 0.8 = 800 kg/hr of water
- Percent solids balance:
(1000 kg/hr)(1 – 0.8) = W(0) + (1 – 0.02 – 0.3)P
(1000 kg/hr)(0.2) = (0.68)P
200 kg/hr = 0.68 P
P = 294.12 kg/hr of potato chips
- Water in final product:
294.12 kg/hr × 0.02 = 5.88 kg/hr of water in potato chips
- Percent water balance:
(1000 kg/hr)(0.8) = W(1) + 5.88 kg/hr
W = 800 kg/hr – 5.88 kg/hr
W = 794.12 kg of water removed from raw potatoes in one hour
- (b) Determine the amount of oil per hour added to the potato chips in the fryer.
Chips have 30% oil. Thus,
-
\( 0.30 = \frac{\text{oil in chips (kg/hr)}}{\text{total weight of chips (kg/hr)}} \)
-
\( 0.30 = \frac{\text{oil in chips (kg/hr)}}{294.12\text{ (kg/hr)}} \)
oil in chips = (0.30) × 294.12 kg/hr
oil in chips = 88.24 kg/hr
- (c) Determine number of bags per 8-hr day:
amount of chips per day = (294.12 kg/hr) × 8 hr/day
= 2,352.96 kg chips/day × (1000 g/kg) = 2,352,960 g/day
number of bags per day = (2,352,960 g/day) × (1 bag/50 g)
= 47,059 bags per day
This example illustrates how the engineer uses knowledge of material balances and food composition to determine production throughput of a continuous fryer.
Example \(\PageIndex{5}\)
Example 5: Energy requirement for an industrial fryer
Problem:
For an industrial fryer with a production capacity of 5,000 kg of corn chips per hour, how much energy is required to reduce the water content of the pre-baked masa (the product that will be fried to make the chips) from 50% w.b. to 4% w.b.? If the frying time takes 60 seconds at a frying temperature of 180°C, calculate:
- (a) initial feed rate of the chips,
- (b) total amount of water removed,
- (c) amount of heat required to evaporate the water,
- (d) total energy required for the frying process, and
- (e) power required for the frying system.
Assume that the oil has already been pre-heated, the temperature of the oil does not drop during frying, but heat is needed to increase the corn chips feed temperature from 25°C to the frying temperature. The specific heat capacity (Cp) of the cooking oil is 2.0 kJ kg−1 °C−1, the specific heats of the corn chips before and after frying are 2.9 kJ kg °C−1 and 1.2 kJ kg°C−1, respectively, and the latent heat of evaporation of water at 100°C is 2,256 kJ/kg. (Hint: 1 kW = 1 kJ/s and water evaporates at 100°C.)
Solution
Calculate the initial mass of the pre-baked masa using Equation 6.3.5:
\( \%\ w.b. = (\frac{\text{water content (kg)}}{\text{total weight of product (kg)}}) \cdot 100 \) (Equation \(\PageIndex{5}\))
4% = (kg of water/5,000 kg)
weight of water = 200 kg
weight of solid = 5,000 kg – 200 kg = 4,800 kg
MC = 50% w.b.
Find the mass of water using Equation 6.3.5:
50% = (kg of water/(kg of water + kg of solid))
50% = W/(W + 4,800 kg)
0.5× (W + 4,800 kg) = W
W = (0.5 × 4,800 kg)/(1 – 0.5)
weight of water = 4,800 kg
Initial feed rate of corn chips = weight of water + weight of solid = 9,600 kg/hr
Calculate the amount of water removed as initial – final:
Initial weight of water = 4,800 kg
Final weight of water = 200 kg
Water removed = 4,800 – 200 = 4,600 kg
Calculate Q required to remove the water (to evaporate the water)
Q = water removed × latent heat of evaporation
Q = (4,600 kg × 2,256 kJ/kg)
Q = 10,377,600 kJ
Calculate sensible heat (25° – 100°C and 100° – 180°C) using Equation 6.3.3:
\( Q=\Delta H = \dot{m}C_{p}\Delta T=\dot{m}C_{p}(T_{1}-T_{2}) \) (Equation \(\PageIndex{3}\))
Q = (9,600 kg) × (2.9 kJ/kg °C) × (100°C – 25°C)
Q = 2,088,000 kJ
Likewise for 100° – 180°C,
Q = (5,000 kg) × (1.2 kJ/kg °C) × (180°C – 100°C)
Q = 4,800,000 kJ
Calculate total Q as the sum of both sensible and latent heat:
Qtotal = Qsensible + Qlatent
Qtotal = 2,088,000 kJ + 4,800,000 kJ + 10,277,600 kJ = 17,265,600 kJ
Calculate power as total heat per unit time:
Power = Q/t
t = 60 seconds
Q = 17,265,600 kJ
Power = 287,760 kW
Example \(\PageIndex{6}\)
Example 6: Water removal rate during frying
Problem:
12 kilograms of fresh bananas were purchased at 0.50 US$/kg. After 4 kg of peel were removed, the bananas were sliced 2 mm thick and vacuum fried at 110°C for 45 minutes. This process reduced the moisture content from 75% w.b. to 2.5% w.b. Determine the rate of water removed from the fresh peeled bananas (kg/min) during the frying process. Assume bananas are composed of water and solids, and that the amount of oil absorbed is negligible (oil content = 0%).
Solution
Draw a schematic of the problem, enter the given data, and identify the unknowns. Then, write down the material balance equations and solve for the unknowns.
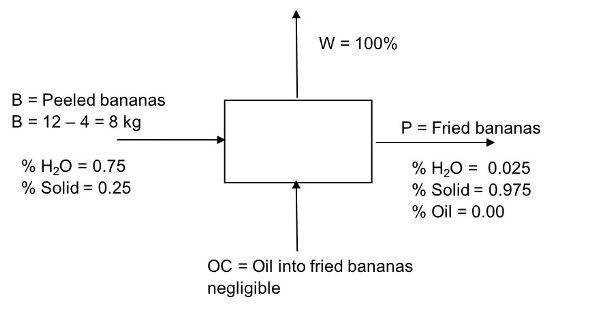
Total material balance: in = out
Remember that oil is zero in this example. Therefore, B = W + P
- Solids balance: (0.25)B = (0)W + (0.975)P
- Water balance: (0.75)B = (1.00)W + (0.025)P
From B = 8 kg, find P from the solids balance:
P = (0.25)(8 kg)/(0.975)
P = 2.05 kg of fried bananas
From the total material balance, find the amount of water removed during the process:
W = B – P = 8 kg – 2.05 kg
W = 5.95 kg of water removed from the fresh peeled bananas
The rate of water removal is the amount of water removed per unit time. Since the frying time was 45 minutes the rate of water removal in is:
rate of water removal = (5.95 kg)/(45 min)
rate of water removal = 0.132 kg water/min
Why is this important? In a vacuum frying process, water is removed from the product during frying, trapped, and separated before it reaches the vacuum pump in order to maintain low pressure inside the frying system. The volume of the water trap and the capacity of the vacuum pump are needed in order to select the most efficient vacuum pump and heat exchanger for cooling the water vapor from the fryer. For example, if 20 kg of potato chips with an initial moisture content of 60% w.b. is fried, it can be assumed that almost 12 kg of water (approximately 12 L) must be removed and collected in a water trap. If the water is not condensed and collected, it will enter the pump and cause a decrease in vacuum pressure.
Image Credits
Figure 1. Yamsaengsung, R. (CC By 4.0). (2014). General schematic of the heat and mass transfer processes occurring during frying of a food product.
Figure 2. Yamsaengsung, R. (CC By 4.0). (2002). Schematic of non-hygroscopic and hygroscopic material.
Figure 3. Yamsaengsung, R. (CC By 4.0). (2020). Typical drying curve (frying curve) showing the constant rate period and the falling rate period.
Figure 4. Yamsaengsung, R. (CC By 4.0). (2020). Process for a simple mass balance consisting of air and water entering and leaving a system.
Figure 5. Yamsaengsung, R. (CC By 4.0). (2020). A schematic of the problem with the given data and the unknowns.
Figure 6. Yamsaengsung, R. (CC By 4.0). (2014). Schematic of a vacuum frying operation.
Example 1. Yamsaengsung, R. (CC By 4.0). (2020). Example 1: Material Balances.
Example 2. Yamsaengsung, R. (CC By 4.0). (2020). Example 2: Moisture content of fried chips.
Example 3. Yamsaengsung, R. (CC By 4.0). (2020). Example 3: Drying curve.
Example 4. Yamsaengsung, R. (CC By 4.0). (2020). Example 4: Production throughput of a continuous fryer.
Example 6. Yamsaengsung, R. (CC By 4.0). (2020). Example 6: Water removal rate during frying.
References
Alvis, A., Velez, C., Rada-Mendoza, M., Villamiel, M., & Villada, H.S. (2009). Heat transfer coefficient during deep-fat frying. Food Control 20(4), 321-325.
Official methods and recommended practices of the AOCS. Urbana, Ill.: American Oil Chemists’ Society.
Choe, E., & Min, D.B. (2007). Chemistry of deep-fat frying oils. J. Food Sci. 72(5), R77-R86.
Engineering ToolBox. (2003). Convective Heat Transfer. Available at: https://www.engineeringtoolbox.com/convective-heat-transfer-d_430.html.
EUFIC. (2014). Facts on fats: The basics. The European Food Information Council. Retrieved from https://www.eufic.org/en/whats-in-food/article/facts-on-fats-the-basics.
Farkas, B. E., Singh, R. P., and Rumsey, T. R. (1996). Modeling heat and mass transfer in immersion frying, part I: Model development. J. Food Eng. 29(1996), 211-226.
Farinu, A., & Baik, O. D. (2007). Heat transfer coefficients during deep fat frying of sweetpotato: Effects of product size and oil temperature. J. Food Res. 40(8), 989-994.
Figura, L. O., & Teixeira, A. A. (2007). Food physics: Physical properties—Measurement and applications. Germany: Springer.
Fito, P. (1994). Modelling of vacuum osmotic dehydration of foods. J. Food Eng. 22(1-4), 313-328.
Garayo, J. and Moreira, R.G. (2002). Vacuum frying of potato chips. J. Food Eng. 55(2), 181-191. dx.doi.org/10.1016/S0260-8774(02)00062-6.
Goswami, G., Bora, R., Rathore, M.S. (2015). Oxidation of cooking oils due to repeated frying and human health. Int. J. Sci. Technol. Manag. 4(1), 495-501.
Guillaume C., De Alzaa, F., & Ravetti, L. (2018). Evaluation of chemical and physical changes in different commercial oils during heating. Acta Sci. Nutri. Health 26(2018), 2-11.
Himmelblau, D. M. (1996). Basic principles in chemical engineering. London: Prentice Hall Int.
Krokida, M. K., Zogzas, N. P., & Maroulis, Z. B. (2002) Heat transfer coefficient in food processing: Compilation of literature data. Int. J. Food Prop., 5:2: 435-450. doi.org/10.1081/JFP-120005796.
Mir-Bel, J., Oria, R., & Salvador, M. L. (2012). Influence of temperature on heat transfer coefficient during moderate vacuum deep-fat frying. J. Food Eng. 113(2012), 167-176.
Moreira, R. G., & Barrufet, N. A. (1998). A new approach to describe oil absorption in fried foods: A simulation study. J. Food Eng. 35:1-22.
Moreira, R. G., Castell-Perez, M. E., & Barrufet, M. A. (1999). Deep-fat frying: Fundamentals and applications. Gaithersburg, MD: Aspen Publishers.
Pandey, A., & Moreira, R. G. (2012). Batch vacuum frying system analysis for potato chips. J. Food Process. Eng. 35(2012), 863-873.
Rani, A. K. S., Reddy, S. Y., & Chetana, R. (2010). Quality changes in trans and trans free fats/oils and products during frying. Eur. Food Res. Technol. 230(6), 803–811.
Shyu, S., & Hwang, L. S. (2001). Effect of processing conditions on the quality of vacuum fried apple chips. Food Res. Int. 34(2001), 133-142.
Sikorski, Z. E., & Kolakowska, A. (2002). Chemical and functional properties of food lipids. United Kingdom: CRC Press.
Wu, H., Tassou, S. A., Karayiammis, T. G., & Jouhara, H. (2013). Analysis and simulation of continuous frying processes. Appl. Thermal Eng. 53(2), 332-339. https://doi.org/10.1016/j.applthermaleng.2012.04.023.
Yamsaengsung, R., & Moreira, R. G. (2002). Modeling the transport phenomena and structural changes during deep fat frying Part I: model development. J. Food Eng. 53(2002), 1-10.
Yamsaengsung, R., Rungsee, C., & Prasertsit, K. 2008. Modeling the heat and mass transfer processes during the vacuum frying of potato chips. Songklanakarin J. Sci. Technol., 31(1), 109–115.
Yamsaengsung, R., & Rungsee, C. 2003. Vacuum frying of fruits and vegetables. Proc. 3th Ann. Conf. Thai Chem. Eng. Appl. Chem., Nakhon Nayok, Thailand, B-11.
Yamsaengsung, R. (2014). Food product development: Fundamentals for innovations. Hat Yai: Apple Art Printing House.


