7.3: Viscous effects
- Page ID
- 18079
Here we will extend the vorticity equation to cover viscous effects, then use the result to develop a simple model of a vortex in a viscous fluid.
7.3.1 The vorticity equation for a viscous fluid
Assume \(\rho=\rho_0\) and that \(ν\) is uniform but nonzero. The momentum equation Equation 6.8.2 is then
\[\frac{D \vec{u}}{D t}=\vec{g}-\vec{\nabla} \frac{p}{\rho_{0}}+v \nabla^{2} \vec{u}.\label{eqn:1} \]
As before, we obtain the vorticity equation by taking the curl of the momentum equation, in this case Equation \(\ref{eqn:1}\). Happily we have already done most of the work; we need only add the viscous term. This is simply
\[\vec{\nabla} \times\left(v \nabla^{2} \vec{u}\right)=v \nabla^{2}(\vec{\nabla} \times \vec{u})=v \nabla^{2} \vec{\omega}. \nonumber \]
The curl of Equation \(\ref{eqn:1}\) is therefore
\[\frac{D \vec{\omega}}{D t}=[\vec{\omega} \cdot \vec{\nabla}] \vec{u}+v \nabla^{2} \vec{\omega}.\label{eqn:2} \]
The final term tells us that vorticity is diffused by viscosity in the same manner as is velocity cf. Equation \(\ref{eqn:1}\).
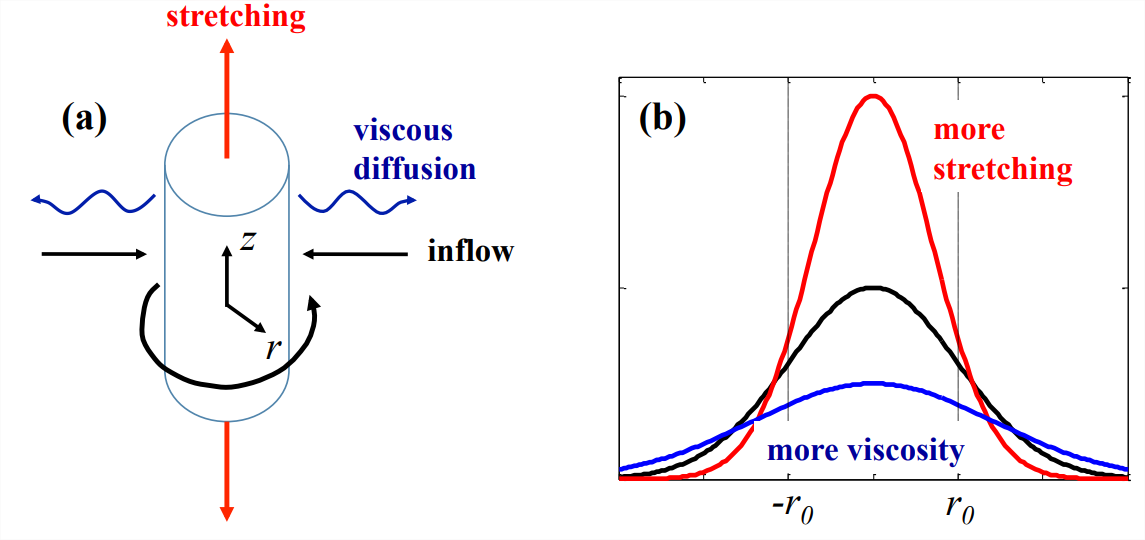
7.3.2 The Burgers vortex
In the presence of viscosity, vortex tubes are no longer immortal due to Kelvin’s theorem. They can, however, be maintained against viscous diffusion by vortex stretching. The Burgers1 vortex is a simple model of an axisymmetric vortex that is simultaneously amplified by extensional strain and diffused by viscosity (Figure \(\PageIndex{1}\)a) such that equilibrium is maintained, i.e., \(\partial\vec{\omega}/\partial t = 0\). The flow has two components: a strain field with expansion in the axial (\(z\)) direction balanced by compression in the radial (\(r\)) direction and a vortex whose motion is entirely azimuthal. We will define these fields in turn, and then test the resulting solution as a model for naturally occurring vortices.
We begin by defining the extensional strain component in the simplest possible way:
\[w=\lambda z.\label{eqn:3} \]
To deduce the corresponding radial velocity, we invoke incompressibility using the divergence in cylindrical coordinates Equation I.1.2:
\[\vec{\nabla} \cdot \vec{u}=\frac{1}{r} \frac{\partial}{\partial r}\left(r u_{r}\right)+\frac{1}{r} \frac{\partial u_{\theta}}{\partial \theta}+\frac{\partial w}{\partial z}=0. \nonumber \]
Axisymmetry requires that \(\partial/\partial\theta\) be zero, so the second term on the right-hand side vanishes, while the third term is just \(\lambda\). This leads to a simple equation for \(u_r\)
\[\frac{\partial}{\partial r}\left(r u_{r}\right)=-\lambda r, \nonumber \]
which integrates to give
\[u_{r}=-\frac{1}{2} \lambda r.\label{eqn:4} \]
So we have the assumed vertical extension Equation \(\ref{eqn:3}\) balanced by a radial inflow Equation \(\ref{eqn:4}\), as illustrated in Figure \(\PageIndex{1}\)a.
We next solve for the vorticity. Recall that, for an axisymmetric vortex,
\[\vec{\omega}=\omega(r) \hat{e}^{(z)}, \nonumber \]
so we only have to determine the scalar function \(\omega(r)\). We do this using the \(z\)-component of Equation \(\ref{eqn:2}\):
\[\frac{D \omega}{D t}=\left[\omega \frac{\partial}{\partial z}\right] w+v \nabla^{2} \omega.\label{eqn:5} \]
The first term on the right-hand side is just \(\omega\lambda\), but there is complexity hidden in the cylindrical forms of the material derivative and the Laplacian. The material derivative of \(\omega\) is Equation I.1.6
\[\begin{align}
\frac{D \omega}{D t} &=\left(\frac{\partial}{\partial t}+u_{r} \frac{\partial}{\partial r}+\frac{u_{\theta}}{r} \frac{\partial}{\partial \theta}+u_{z} \frac{\partial}{\partial z}\right) \omega, \\
&=-\frac{1}{2} \lambda r \frac{d \omega}{d r}\label{eqn:6}
\end{align} \nonumber \]
The total derivative is written because \(\omega\) depends only on \(r\). The Laplacian of \(\omega\) Equation I.1.4 is
\[\begin{align}
\nabla^{2} \omega &=\left(\frac{1}{r} \frac{\partial}{\partial r} r \frac{\partial}{\partial r}+\frac{1}{r^{2}} \frac{\partial^{2}}{\partial \theta^{2}}+\frac{\partial^{2}}{\partial z^{2}}\right) \omega, \\
&=\frac{1}{r} \frac{d}{d r}\left(r \frac{d \omega}{d r}\right)\label{eqn:7}
\end{align} \nonumber \]
Substituting Equation \(\ref{eqn:6}\) and Equation \(\ref{eqn:7}\) into Equation \(\ref{eqn:5}\) we obtain an ordinary differential equation for \(\omega(r)\):
\[-\frac{1}{2} \lambda r \frac{d \omega}{d r}=\omega \lambda+\frac{\mathrm{v}}{r} \frac{d}{d r}\left(r \frac{d \omega}{d r}\right). \nonumber \]
Multiplying through by \(r\) and integrating yields
\[vr \frac{d \omega}{d r}+\lambda \frac{1}{2} r^{2} \omega=0, \nonumber \]
or
\[\frac{d \omega}{d r}=-\frac{\lambda}{2 \mathrm{v}} r \omega. \nonumber \]
The solution is a Gaussian function:
\[\omega=\omega_{0} e^{-\frac{\lambda}{4 v} r^{2}}, \nonumber \]
where \(\omega_0\) is an arbitrary constant representing the maximum vorticity. This is more commonly written as
\[\omega(r)=\frac{\Gamma}{2 \pi r_{0}^{2}} \exp \left(-\frac{r^{2}}{2 r_{0}^{2}}\right), \quad \text { where } r_{0}=\sqrt{\frac{2 v}{\lambda}}.\label{eqn:8} \]
The balance between stretching and viscosity is expressed in the radial scale \(r_0\) (Figure \(\PageIndex{1}\)b). Stronger stretching gives a thinner, more intense vortex; stronger viscosity gives a thicker, weaker vortex.
Vortices at the dissipation scale In a turbulent flow, the vorticity field has the form of a spaghetti-like tangle of vortex tubes (e.g., Moffatt et al. 1994). Is the Burgers model applicable to these structures? The smallest turbulent motions are of the order of the Kolmogorov scale, \(L_K=(v^3/\varepsilon)^\frac{1}{4}\), where \(\varepsilon\) is the kinetic energy dissipation rate \(\varepsilon = 2ve_{ij}e_{ij}\). In geophysical turbulence, \(\varepsilon\) varies greatly, but \(L_K\) varies less because of the power 1/4; a typical value is ∼ 1 cm. In the Burgers model, the only nonzero strain rate component is \(e_{33}=\lambda\), and therefore \(\varepsilon = 2v\lambda^2\). The Burgers model predicts \(r_0 = 1.7 L_K\). The agreement is reasonable in an order-of-magnitude sense.
Test your understanding: Of the simplifying assumptions that underlie the Burgers model, which are most likely to be wrong in this case?
A tornado as a Burgers vortex Suppose that a tornado is driven by a vertical expansion \(dw/dz = \lambda = 0.1\ s^{-1}\). This would correspond, for example, to an updraft of 50 m/s at a height of 500 m. For air, \(ν\) = 10−5m2/s. These values lead to \(r_0\) ∼ 10−2 m, far too small to be realistic. Clearly at least one simplifying assumption is wrong. For example, tornados are not usually cylindrical but are more funnelshaped. A more extreme discrepancy, though, is in the very simple, symmetric form of the velocity field. In reality, tornadoes are intensely turbulent. The effect of turbulence on the overall flow is similar to that of a greatly increased viscosity. To get \(r_0\) = 30 m, a reasonable value, we must assume that this “turbulent” viscosity (or “eddy” viscosity, see section 6.3.6) is 102 m2/s.
1Johannes Martinus (Jan) Burgers was a Dutch physicist best known for the Burgers equation, which describes nonlinear-diffusive systems.


