9.2: Hydraulic Control
- Page ID
- 18086
Here we will look at the phenomenon of hydraulic control, which constrains the state of flow over an obstacle. For this initial look we will assume that the flow takes place in a channel of rectangular cross-section.
9.2.1 Equations of motion for flow in a rectangular channel
We now use these assumptions to simplify the equations of motion. The momentum equation for inviscid, homogeneous flow is
\[\rho_{0} \frac{D \vec{u}}{D t}=-\rho_{0} g \hat{e}^{(z)}-\vec{\nabla} p. \nonumber \]
Substituting assumption 5.1, this becomes
\[\rho_{0} \frac{D \vec{u}}{D t}=-\rho_{0} g \hat{e}^{(z)}-\rho_{0} g\left(\vec{\nabla} \eta-\hat{e}^{(z)}\right)=-\rho_{0} g \vec{\nabla} \eta, \nonumber \]
and the streamwise (\(x\)) component is
\[\frac{D u}{D t}=u_{t}+u u_{x}+\cancelto{0}{v u_{y}}+\cancelto{0}{w u_{z}}=-g \eta_{x}, \nonumber \]
where subscripts indicate partial derivatives. Our streamwise momentum equation is now
\[u_{t}+u u_{x}=-g \eta_{x}.\label{eqn:1} \]
Mass conservation is expressed by \(\vec{\nabla}\cdot\vec{u}=0\). Integrating this over \(z\) gives
\[\int_{-H+h(x)}^{\eta(x, t)}\left(u_{x}+w_{z}\right) d z=0. \nonumber \]
Because \(u\) is independent of \(z\) (assumption 5.1), we can take the first term out of the integral, while the second term integrates trivially:
\[u_{x}(\eta+H-h)+\left.w\right|_{-H+h} ^{\eta}=0.\label{eqn:2} \]
Both the surface and the bottom boundary are material surfaces, so the boundary conditions on \(w\) are:
\[\begin{aligned}
\left.w\right|_{z=\eta} &=\frac{D \eta}{D t}=\eta_{t}+u \eta_{x} \\
\left.w\right|_{z=-H+h(x)} &=\frac{D}{D t}(-H+h)=\underbrace{h_{t}}_{=0}+u h_{x}=u h_{x}.
\end{aligned} \nonumber \]
Combining these, we have
\[\left.w\right|_{-H+h} ^{\eta}=\eta_{t}+u \eta_{x}-u h_{x}. \nonumber \]
Substituting this into Equation \(\ref{eqn:2}\) gives
\[\eta_{t}+u \eta_{x}-u h_{x}+u_{x}(\eta+H-h)=0.\label{eqn:3} \]
Insight into Equation \(\ref{eqn:3}\) may be gained by interpreting it in terms of the volume flux:
\[Q=u A=u W \underbrace{(\eta+H-h)}_{\text {total depth }}. \nonumber \]
In Equation \(\ref{eqn:3}\), note that the 2nd and 3rd terms are equivalent to \(u(\eta +H −h)x\), since \(H\) is a constant. Therefore:
\[\eta_{t}+u(\eta+H-h)_{x}+u_{x}(\eta+H-h)=\eta_{t}+[u(\eta+H-h)]_{x}=0, \nonumber \]
or,
\[\eta_{t}=-\frac{Q_{x}}{W}.\label{eqn:4} \]
So Equation \(\ref{eqn:3}\) tells us that the surface moves up and down so as to balance convergences and divergences in the volume flux.
9.2.2 Steady flow and the Froude number
In a steady flow, time derivatives are zero and Equation \(\ref{eqn:1}\) and Equation \(\ref{eqn:3}\) can be written as
\[u u_{x}=-g \eta_{x},\label{eqn:5} \]
\[u \eta_{x}+u_{x}(\eta+H-h)=u h_{x}.\label{eqn:6} \]
We now multiply Equation \(\ref{eqn:6}\) by \(u\):
\[u^{2} \eta_{x}+(\eta+H-h) u u_{x}=u^{2} h_{x} \nonumber \]
and substitute Equation \(\ref{eqn:5}\):
\[u^{2} \eta_{x}-(\eta+H-h) g \eta_{x}=u^{2} h_{x}. \nonumber \]
Note that we now have \(\eta_x\) as a factor in both terms on the left-hand side. Dividing by \(g(\eta +H −h)\), we have
\[[\underbrace{\frac{u^{2}}{g(\eta+H-h)}}_{F^{2}}-1] \eta_{x}=\underbrace{\frac{u^{2}}{g(\eta+H-h)}}_{F^{2}} h_{x}. \nonumber \]
The quantity \(u^2/g(\eta +H −h)\) that appears on both sides is the squared velocity over \(g\) times the total water depth. We recognize this as the square of the Froude number (cf. section 8.4.2). In the case of small-amplitude waves over a flat bottom (\(\eta\rightarrow 0\);\(h\) = 0), \(F^2\) matches our previous definition \(u^2/gH\). Recall that flow is supercritical (i.e., no information can propagate upstream) if \(F\) > 1 and subcritical if \(F\) < 1.
In summary, steady flow over an obstacle requires the following relation between the surface and bottom slopes:
\[\left(F^{2}-1\right) \eta_{x}=F^{2} h_{x},\label{eqn:7} \]
where
\[F=\frac{|u|}{\sqrt{g(\eta+H-h)}}.\label{eqn:8} \]
An obstacle of small amplitude
If the amplitudes of the surface deflection and the bottom topography are small compared to the water depth, the Froude number can be treated as a constant, allowing us to integrate Equation \(\ref{eqn:7}\). To see this, suppose that \(u\) is close to its upstream value \(u_0\) and \(|\eta| \ll H\) and \(|h| \ll H\). In that case the Froude number is nearly constant:
\[F=F_{0}+F^{\prime}, \nonumber \]
where \(F_0 = |u_0|/ \sqrt{gH}\) and \(F^\prime\) is the perturbation caused by nonzero (but small) perturbations in \(u\), \(\eta\) and \(h\). Then
\[F^{2}=F_{0}^{2}+2 F_{0} F^{\prime}+F^{\prime 2}. \nonumber \]
As we did in section 8.2.1, we discard the term that is a product of small quantities, giving
\[F^{2}=F_{0}^{2}+2 F_{0} F^{\prime}. \nonumber \]
Substituting into Equation \(\ref{eqn:7}\), we now have
\[\left(F_{0}^{2}+2 F_{0} F^{\prime}-1\right) \eta_{x}^{\prime}=\left(F_{0}^{2}+2 F_{0} F^{\prime}\right) h_{x}^{\prime}, \nonumber \]
where primes have been placed on \(\eta\) and \(h\) to indicate that they are small quantities. Once again we discard the products of primes, and arrive at
\[\left(F_{0}^{2}-1\right) \eta_{x}^{\prime}=F_{0}^{2} h_{x}^{\prime},\label{eqn:9} \]
i.e., fluctuations in \(F\) can be neglected in the limit of small amplitude. We now dispense with the subscripts and primes as they have served their purpose.
Integrating Equation \(\ref{eqn:9}\), we obtain
\[\left(F^{2}-1\right) \eta=F^{2} h+C.\label{eqn:10} \]
We assume that, far upstream, the bottom is flat and there is no surface deflection, so the constant of integration is zero. Hence:
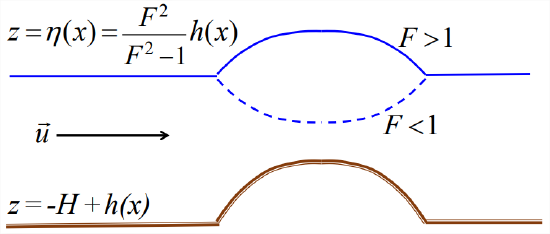
\[\eta=\frac{F^{2}}{F^{2}-1} h./label{eqn:11} \nonumber \]
So the surface deflection over a small bump depends on the flow speed, as shown in Figure \(\PageIndex{2}\). If the flow is fast enough to make \(F\) > 1, then the surface is elevated in proportion to the topography. If \(F\) < 1, though, the surface deflection is opposite to the topography: low over a bump (dashed curve on Figure \(\PageIndex{2}\)); raised over a deep spot.
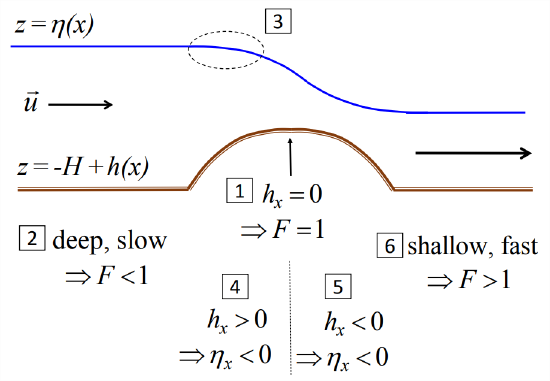
An obstacle of arbitrary amplitude: hydraulic control
From Equation \(\ref{eqn:7}\) we can infer a critical fact about flow over an obstacle:
If \(h_x\) = 0, then either \(\eta_x\) = 0 or \(F\) = 1.
So at a high or low spot in the bottom topography, either the surface is flat or the flow is critical.
In the small-amplitude limit, we have seen that the first condition is satisfied; \(\eta_x\) = 0 at the crest of the obstacle (Figure \(\PageIncdex{2}\)). But in nature, we often observe plunging flow over an obstacle, in which case \(\eta_x\) is not zero (Figure \(\PageIndex{3}\)). In that case, the Froude number can only be 1. This restriction on the flow state is called hydraulic control. Since plunging flow does not happen in the small-amplitude limit, we identify it as a fundamentally nonlinear effect. To explore it we must consider disturbances of arbitary amplitude.
If the amplitudes are not small, we can no longer integrate Equation \(\ref{eqn:7}\) to obtain a quantitative relationship between \(\eta\) and \(h\). Instead, we analyze Equation \(\ref{eqn:7}\) qualitatively. We will do this one step at a time for the case of flow over a bump, with careful reference to Figure \(\PageIndex{3}\).
- At the crest of the bump, \(F\) = 1.
- We therefore expect that \(F\) < 1 upstream of the bump, where the flow is deeper and slower.
- When we first encounter the bump, \(|\eta|\) and \(|h|\) are small, and we therefore expect \(\eta\) to decrease as in the small-amplitude case with \(F\) < 1 (Figure \(\PageIndex{2}\)).
- Approaching the crest of the bump, the disturbance is no longer small, but \(F\) is still less than 1 and \(h_x\) is still positive, so Equation \(\ref{eqn:7}\) tells is that \(\eta\) must continue to drop.
- On the lee side of the bump, \(F\) > 1 and \(h_x\) < 0, so we see from Equation \(\ref{eqn:7}\) that \(\eta_x\) must remain negative.
- Beyond the bump, the increase in \(F\) from subcritical to supercritical values produces relatively shallow, fast flow.
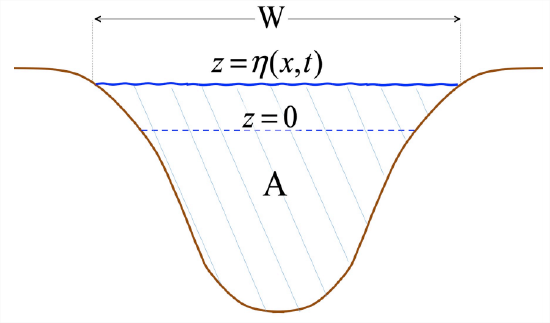
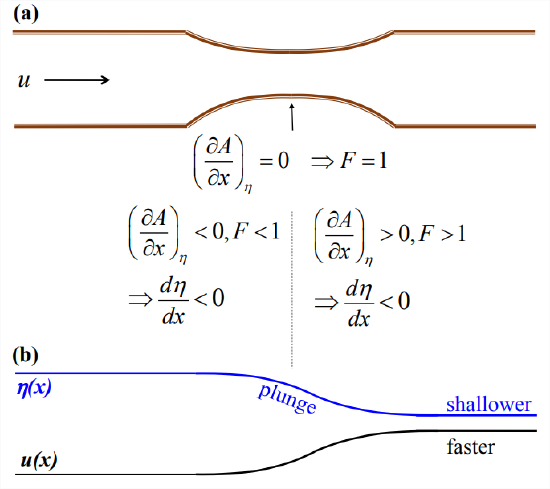
9.2.3 Generalization: a channel of arbitrary cross-section
We now relax the assumption #4 of the previous section, namely that the the channel has rectangular cross-section. Instead, we let the channel have arbitrary shape. The width of the stream is now variable, both in \(x\) as the channel narrows and widens and in \(t\) as the surface elevation changes. We also define the “wetted” cross-sectional area \(A\), which varies in both \(x\) and \(t\) for the same reasons. The only restriction is that we assume the existence of an “upstream” region where the channel shape is uniform in \(x\), the velocity is even and \(\eta\) = 0. We would like to see how \(u\) and \(\eta\) vary in response to changes in the channel shape.
The streamwise momentum equation is now
\[\frac{D u}{D t}=u_{t}+u u_{x}+v u_{y}+\underbrace{w u_{z}}_{=0}=-g \eta_{x}. \nonumber \]
We add a new assumption, namely that the flow is “mostly” streamwise, in the sense that \(|u| \gg |v|\), and/or \(|u_x| \gg |u_y|\). As a result \(|vu_y| \ll |uu_x|\), i.e., the spanwise advection term is negligible, leaving
\[u_{t}+u u_{x}=-g \eta_{x} \nonumber \]
as before. We now assume that the flow is steady (\(u_t\) = 0), and substitute \(u = Q/A\) to obtain
\[\frac{Q}{A} \frac{d}{d x}\left(\frac{Q}{A}\right)=-g \frac{d \eta}{d x},\label{eqn:12} \]
or
\[-\frac{Q^{2}}{A^{3}} \frac{d A}{d x}=-g \frac{d \eta}{d x}.\label{eqn:13} \]
Can we solve this for \(\eta\), and thereby predict the surface response to a given change in channel shape? No, because \(A\) is determined in part by \(\eta\). Considering \(A\) as a function of \(x\) and \(\eta(x)\), the total \(x\)-derivative of \(A\) has two parts:
\[\frac{d A}{d x}=\underbrace{\left(\frac{\partial A}{\partial x}\right)_{\eta}}_{\text {channel shape }}+\underbrace{\left(\frac{\partial A}{\partial \eta}\right)_{x} \frac{d \eta}{d x}}_{\text {water depth }} \nonumber \]
The first term describes variations due only to the shape of the walls, the second only to the surface elevation. Note that the change in \(A\) due to a small change in surface elevation is \(\delta A = W\delta\eta\), so
\[\left(\frac{\partial A}{\partial \eta}\right)_{x}=W, \nonumber \]
and we are left with
\[\frac{u^{2}}{A}\left[\left(\frac{\partial A}{\partial x}\right)_{\eta}+W \frac{d \eta}{d x}\right]=g \frac{d \eta}{d x}. \nonumber \]
We now divide by \(g\) and collect terms proportional to \(d\eta /dx\):
\[\left(\frac{W u^{2}}{g A}-1\right) \frac{d \eta}{d x}=-\frac{u^{2}}{g A}\left(\frac{\partial A}{\partial x}\right)_{\eta}. \nonumber \]
Defining the Froude number as
\[F=\frac{|u|}{\sqrt{g A / W}},\label{eqn:14} \]
we finally have
\[\left(F^{2}-1\right) \frac{d \eta}{d x}=-\frac{F^{2}}{W}\left(\frac{\partial A}{\partial x}\right)_{\eta}.\label{eqn:15} \]
This is a generalization of our previous results Equation \(\ref{eqn:7}\) and Equation \(\ref{eqn:8}\) for the rectilinear channel. In that previous case \(W\) is constant and \(A = W(\eta +H −h)\), giving
from which we recover Equation \(\ref{eqn:7}\) and Equation \(\ref{eqn:8}\).
We can understand plunging flow through an arbitrary constriction in the same way we did in the rectilinear case. Approaching the constriction (Figure \(\PageIndex{eqn:5}\)a), the wetted area decreases. If \(F\) < 1, the elevation must also decrease (\(d\eta/dx < 0\); Figure \(\PageIndex{5}\)b). At the throat of the constriction, \(F\) = 1. Leaving the constriction, the wetted area increases but \(F\) > 1, so the surface continues to descend. Downstream, the flow is supercritical, i.e., shallower and faster.
Figure \(\PageIndex{6}\) shows an example from the Smith River in California. Here, rafters are crossing a hydraulic control caused by a constriction. They will now enjoy (one hopes) an exciting few seconds as they negotiate a hydraulic jump, the subject of the next section.