12: Appendix A- Taylor Series Expansions
- Page ID
- 18038
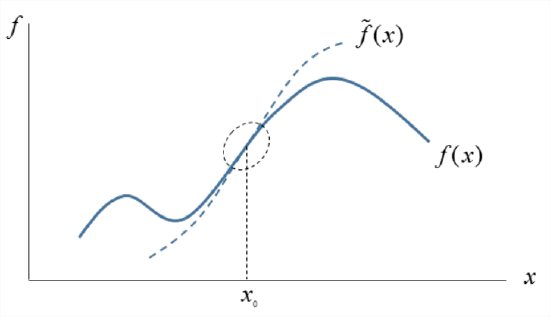
Taylor’s theorem (which we will not prove here) gives us a way to take a complicated function \(f(x)\) and approximate it by a simpler function \(\tilde{f}(x)\). The price of this simplification is that \(\tilde{f} \approx f\) only in a small region surrounding some point \(x = x_0\) (Figure \(\PageIndex{1}\)).
The formula is:
\[\tilde{f}(x)=f\left(x_{0}\right)+f^{\prime}\left(x_{0}\right)\left(x-x_{0}\right)+\frac{1}{2} f^{\prime \prime}\left(x_{0}\right)\left(x-x_{0}\right)^{2}+\frac{1}{6} f^{\prime \prime \prime}\left(x_{0}\right)\left(x-x_{0}\right)^{3}+\dots\label{eqn:1} \]
The sequence goes on forever, but we typically only use the first few terms. To apply (1), we choose a point \(x_0\) where we need the approximation to be accurate. We then compute the derivatives at that point, \(f^\prime(x_0)\, \(f^{\prime\prime} (x_0)\), \(f^{\prime\prime\prime} (x_0)\), etc., for as far as we want to take it. For accuracy, use a lot of terms; for simplicity, use only a few.
For example, if
\[f(x)=(1-x)^{-1} \nonumber \]
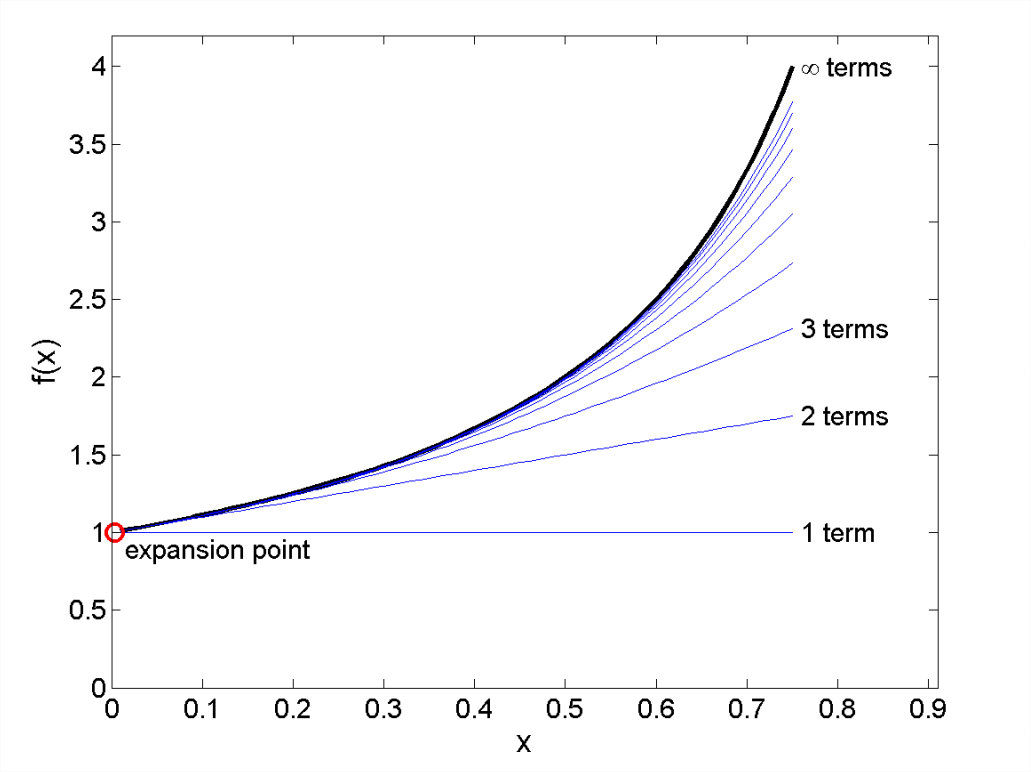
and we choose \(x_0\) = 0, then the Taylor series is just the well-known expression
\[\tilde{f}(x)=1+x+x^2+x^3+\dots. \nonumber \]
Figure A.2 shows the expansion with successively larger numbers of terms retained. Near x0, good accuracy can be achieved with only a few terms. The further you get from x0, the more terms must be retained for a given level of accuracy.
The real benefit of Taylor series is evident when working with more complicated functions. For example, \(f(x) = \sin(\tan(x))\) can be approximated by \(\tilde{f}\) = \(x\) for \(x\) close to zero.
Note that the first - order terms in Equation \(\ref{eqn:1}\):
\[\tilde{f}(x)=f(x_0)+f^\prime(x_0)(x-x_0), \nonumber \]
give a valid approximation of \(f(x)\) in the limit \(x \rightarrow x_0\), and can be rearranged to form the familiar definition of the first derivative:
\[f^\prime(x_0)=\lim{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0} \nonumber \]
The Taylor series expansion technique can be generalized for use with multivariate functions. Suppose that \(f = f(\vec{x})\), where \(\vec{x} = (x, y)\). Then
\[\tilde{f}(\vec{x})=f(\vec{x_0})+f_x(\vec{x_0})\delta x+ f_y(\vec{x_0})\delta y + \frac{1}{2} f_{xx}(\vec{x_0})\delta x^2 + f_{xy}(\vec{x_0})\delta_x\delta_y+\frac{1}{2}f_{yy}(\vec{x_0})\delta_{y^2}+\dots,\label{eqn:2} \]
where \(\delta_x=x-x_0\), \(\delta_y=y-y_0\) and subscripts denote partial derivatives. Note that the first - order terms in Equation \(\ref{eqn:2}\) can be written using the directional derivative:
\[f(\vec{x})=f(\vec{x_0})+\vec{\nabla}f(\vec{x_0})\cdot\delta \vec{x}. \nonumber \]
You will notice that \(\tilde{f}\) has been replaced by \(f\); this is valid in the limit \(\vec{x} \rightarrow \vec{x_0}\), or \(\delta \vec{x} \rightarrow 0\).