13.2: The Moment of Inertia Tensor
- Page ID
- 18090
The angle \(\theta\) increases in time (if you push hard enough1) in accordance with
\[\vec{T}=\underset{\sim}{I}\vec{\alpha},\label{eqn:1} \]
in which \(\vec{\alpha}\) is the angular acceleration and \(\underset{\sim}{I}\) is a matrix called the moment of inertia. For the simple case shown in Figure 13.1.1, \(\underset{\sim}{I}\) is proportional to the identity matrix \(\underset{\sim}{\delta}\), \(\vec{\alpha}\) is parallel to the axis of rotation (the bolt), and its magnitude \(|\vec{\alpha}|\) is \(d^2\theta/dt^2\).
The general definition of the moment of inertia matrix is
\[I_{i j}=\int_{V} d V \rho(\vec{x})\left(x_{k} x_{k} \delta_{i j}-x_{i} x_{j}\right),\label{eqn:2} \]
where \(\rho(\vec{x})\) is the density (mass per unit volume). Details can be found in most classical mechanics texts, e.g., Marion (2013).
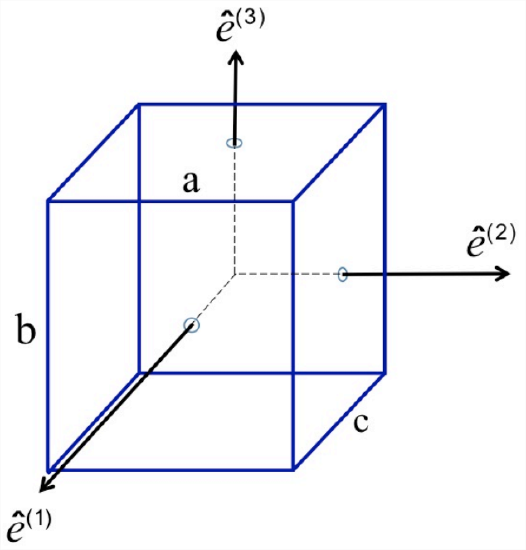
The particular case illustrated in Figure \(\PageIndex{1}\) is the rotation of a rectangular prism, with uniform density and edge dimensions \(a\), \(b\) and \(c\), about the \(\hat{e}^{(1)}\) axis. In this case both torque and angular acceleration are parallel to \(\hat{e}^{(1)}\), and the only nonzero component of \(\underset{\sim}{I}\) is \(I_{11}\), computed as follows:
\[\begin{aligned}
I_{11} &=\int_{V} d V \rho\left(x_{2}^{2}+x_{3}^{2}\right) \\
&=\rho \int_{-a / 2}^{a / 2} d x_{1} \int_{-b / 2}^{b / 2} d x_{2} \int_{-c / 2}^{c / 2} d x_{3}\left(x_{2}^{2}+x_{3}^{2}\right) \\
&=\rho \frac{a b c\left(b^{2}+c^{2}\right)}{12}.
\end{aligned} \nonumber \]
For the simple case of a cube with \(a\) = \(b\) = \(c\) = \(\Delta\),
Is the moment of inertia matrix \(\underset{\sim}{I}\) a tensor? We would expect so, since it connects two physically real vectors via Equation \(\ref{eqn:1}\). We can also establish this directly from Equation \(\ref{eqn:2}\), the general formula for \(\underset{\sim}{I}\). Like any other integral, \(\underset{\sim}{I}\) can be written as the limit of a sum:
\[I_{i j}=\sum \Delta V \rho\left(x_{k} x_{k} \delta_{i j}-x_{i} x_{j}\right), \nonumber \]
where each term in the sum is evaluated at the center of a volume element \(\Delta V\). Now \(\Delta V\) and \(\rho\) are scalars, and so is the dot product \(x_k x_k\) (section 3.2). Moreover, we know that both \(\delta_{ij}\) and the dyad \(x_ix_j\) transform according to Equation 3.3.8. Each term in the sum is therefore a tensor, and so then is the sum itself. Taking the limit as \(\Delta V\rightarrow 0\), we conclude that \(\underset{\sim}{I}\) transforms according to Equation 3.3.8. We therefore refer to \(\underset{\sim}{I}\) as the moment of inertia tensor.
1In the case shown here, \(\vec{F}\) is really the sum of the force exerted by the person and the opposing force exerted by friction, and similarly for \(\vec{T}\).


