15.3: D.3 Applications of \(\epsilon\)
- Page ID
- 18112
In this section we will look at three fundamental algebraic operations that are based on \(\underset{\sim}{\varepsilon}\): the cross product, the triple product and the determinant. We will see how each can be interpreted geometrically in terms of areas and volumes, and derive their most useful properties.
D.3.1 The cross product
One function of a 3rd-order tensor is to define a mathematical relationship between three vectors, e.g., a way to multiply two vectors to get a third vector. To be generally useful, such an operation should work the same in every reference frame, i.e., the tensor should be isotropic. Because \(\underset{\sim}{\varepsilon}\) is the only isotropic 3rd-order tensor, there is only one such operation:
\[z_{k}=\varepsilon_{i j k} u_{i} v_{j}.\label{eqn:1} \]
This is the \(k\)th component of the familiar cross (or vector) product: \(\vec{z}\) = \(\vec{u}\times\vec{v}\) whose properties were discussed in section 3.3.7.
D.3.2 The triple product
The triple product of three vectors \(\vec{u}\), \(\vec{v}\) and \(\vec{w}\) is a trilinear scalar product given by
\[T=(\vec{u} \times \vec{v}) \cdot \vec{w}=\varepsilon_{i j k} u_{i} v_{j} w_{k}.\label{eqn:2} \]
Because \(\underset{\sim}{\varepsilon}\) is the only isotropic 3rd-order tensor, the triple product is the only trilinear scalar product that is computed the same way in all reference frames. We now derive some algebraic and geometrical properties of the triple product.
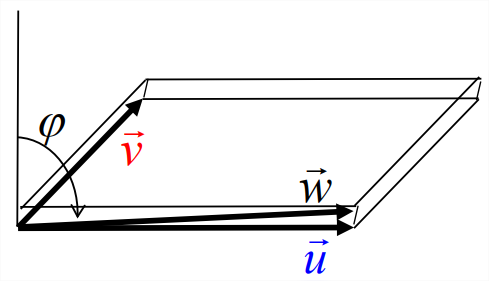
- The triple product is equal to the volume \(V\) of the parallelepiped enclosed by the three vectors (Figure \(\PageIndex{1}\)), give or take a minus sign. The plane that encloses \(\vec{u}\) and \(\vec{v}\) divides space into two half-spaces, and the cross product \(\vec{u}\times\vec{v}\) extends into one or the other of those half-spaces, determined by the right-hand rule. If \(\vec{w}\) points into the same half-space as the cross product (i.e., the angle \(\phi\), defined in Figure \(\PageIndex{1}\), is acute), \(\vec{u}\), \(\vec{v}\) and \(\vec{w}\) are called a right-handed triple, a distinction that will be of great use to us. In this case, the triple product \(T\) is positive and is equal to the volume \(V\). Conversely, if \(\vec{u}\), \(\vec{v}\) and \(\vec{w}\) form a left-handed triple (\(\phi\) obtuse), \(T\) = \(-V\).
- The triple product is unchanged by a cyclic permutation of \(\vec{u}\), \(\vec{v}\) and \(\vec{w}\), i.e. \[(\vec{u} \times \vec{v}) \cdot \vec{w}=(\vec{w} \times \vec{u}) \cdot \vec{v}=(\vec{v} \times \vec{w}) \cdot \vec{u}. \nonumber \] This follows from Equation \(\ref{eqn:2}\) and the invariance of \(\underset{\sim}{\varepsilon}\) to cyclic permutations. Geometrically, a cyclic permutation corresponds to a rotation of the parallelepiped, which obviously leaves its volume unchanged.
- Interchanging any two of \(\vec{u}\), \(\vec{v}\) and \(\vec{w}\) changes the sign of the triple product. This is seen easily as a consequence of Equation \(\ref{eqn:2}\) and the complete antisymmetry of \(\underset{\sim}{\varepsilon}\). Geometrically, it means that the parity of the set {\(\vec{u}\),\(\vec{v}\),\(\vec{w}\)} changes from right-handed to left-handed, and hence the triple product changes from \(+V\) to \(-V\).
- Now imagine that the parallelepiped is squashed so that \(\vec{w}\) lies in the plane of \(\vec{u}\) and \(\vec{v}\) (Figure \(\PageIndex{1}\)). Clearly the volume of the parallelepiped goes to zero; hence, the triple product must also go to zero. A special case is if \(\vec{w}\) is equal to either \(\vec{u}\) or \(\vec{v}\). In fact, if any two of \(\vec{u}\), \(\vec{v}\) and \(\vec{w}\) are equal, the triple product is zero.
Properties 2-4 above can be expressed succinctly using \(\underset{\sim}{\epsilon}\). Suppose we relabel our three vectors \(\vec{u}\), \(\vec{v}\) and \(\vec{w}\) as \(\vec{u}(i)\), \(\vec{u}(j)\) and \(\vec{u}(k)\), where \(i\), \(j\) and \(k\) are any combination of 1, 2 and 3 (including those with repeated values). Now let \(T\) stand for the triple product where the indices \(i\), \(j\) and \(k\) actually are 1, 2 and 3, i.e., \(T = (\vec{u}(1) \times \vec{u}(2) )\cdot\vec{u}(3)\). Next, let the indices \(ijk\) be any combination of 1, 2 and 3. The aforementioned properties of the triple product (namely that cyclic permutations change nothing, interchanging changes the sign and setting two vectors equal makes the triple product zero) are equivalent to
\[\left(\vec{u}^{(i)} \times \vec{u}^{(j)}\right) \cdot \vec{u}^{(k)}=T \varepsilon_{i j k}.\label{eqn:3} \]
As a special case, suppose that the \(\vec{u}(i)\) are the basis vectors of a right-handed Cartesian coordinate system \(\hat{e}^{(i)}\), where \(i\) = 1,2,3. In that case the parallelepiped is just a unit cube and
\[\left(\hat{e}^{(i)} \times \hat{e}^{(j)}\right) \cdot \hat{e}^{(k)}=\varepsilon_{i j k}. \nonumber \]
D.3.3 The determinant
Definition and elementary properties
The determinant of a \(3\times 3\) matrix \(\underset{\sim}{A}\) can be written as
\[\operatorname{det}(\underset{\sim}{A})=\varepsilon_{i j k} A_{i 1} A_{j 2} A_{k 3},\label{eqn:4} \]
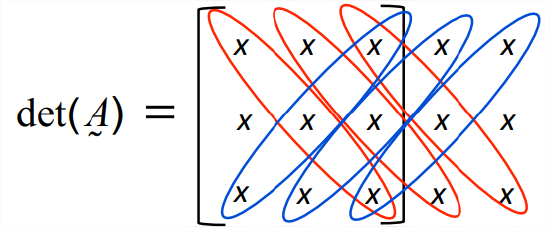
i.e., if we regard the columns as vectors, the determinant is their triple product.1 As taught in elementary algebra classes, the determinant is calculated as a linear combination of multiples of three elements, one from each column (Figure \(\PageIndex{2}\)). Three of those combinations are added, three are subtracted, and the rest have a coefficient of zero. Referring back to Equation 15.1.6, you can check that the coefficients of that linear combination are just the corresponding elements of \(\underset{\sim}{\varepsilon}\).
Referring again to Figure \(\PageIndex{2}\), turn the book sideways and verify that the determinant can just as easily be written as the triple product of rows:
\[\operatorname{det}(\underset{\sim}{A})=\varepsilon_{i j k} A_{1 i} A_{2 j} A_{3 k}\label{eqn:5} \]
The expressions Equation \(\ref{eqn:4}\) and Equation \(\ref{eqn:5}\) lead immediately to several elementary properties of the determinant:
- Transposing the matrix does not change the determinant: \[\operatorname{det}\left(\underset{\sim}{A}^{T}\right)=\operatorname{det}(\underset{\sim}{A}). \nonumber \]
- Interchanging two columns of a matrix changes the sign of the determinant. This corresponds to the fact that \(\underset{\sim}{\varepsilon}\) is antisymmetric with respect to every pair of indices.
- Remembering that transposing does not change the determinant, we can make the same statement about rows: interchanging any two rows changes the sign of the determinant.
- If any two columns (or two rows) are the same, the determinant is zero. This is because elements of \(\underset{\sim}{\varepsilon}\) are zero if two of their indices are the same.
- Finally, because cyclic permutations of the indices of \(\underset{\sim}{\varepsilon}\) make no difference, cyclic permutations of either the rows or the columns of a matrix leave the determinant unchanged.
- As an alternative to the pattern shown in Figure \(\PageIndex{2}\), Equation \(\ref{eqn:4}\) can also be arranged into a formula commonly called the method of cofactors. One chooses a row or column to expand along, then forms a linear combination of \(2\times 2\) subdeterminants. Here is the formula for expanding along the top row: \[\operatorname{det}(A)=A_{11} \operatorname{det}\left(\begin{array}{cc}
A_{22} & A_{23} \\
A_{32} & A_{33}
\end{array}\right)-A_{12} \operatorname{det}\left(\begin{array}{cc}
A_{21} & A_{23} \\
A_{31} & A_{33}
\end{array}\right)+A_{13} \operatorname{det}\left(\begin{array}{cc}
A_{21} & A_{22} \\
A_{31} & A_{32}.\label{eqn:6}
\end{array}\right) \nonumber \] The other expansions work similarly. The minus sign applied to the middle term results from the antisymmetry of \(\underset{\sim}{\varepsilon}\).
Easy mnemonics for the triple and cross products.
The identification of the triple product with \(\underset{\sim}{\varepsilon}\) provides an easy way to calculate it. Just arrange the three vectors \(\vec{u}\), \(\vec{v}\) and \(\vec{w}\) into a matrix:
\[(\vec{u} \times \vec{v}) \cdot \vec{w}=\varepsilon_{i j k} u_{i} v_{j} w_{k}=\operatorname{det}\left(\begin{array}{ccc}
u_{1} & v_{1} & w_{1} \\
u_{2} & v_{2} & w_{2} \\
u_{3} & v_{3} & w_{3}
\end{array}\right),\label{eqn:7} \]
and calculate the determinant using either the elementary formula shown in Figure \(\PageIndex{2}\) or the method of cofactors (e.g., Equation \(\ref{eqn:6}\)).
The cross product of two vectors can be computed by arranging the components of the vectors, together with the three basis vectors, to form a matrix.
\[\vec{u} \times \vec{v}=\varepsilon_{i j k l}, v_{j}, \vec{e}^{(k)}=\operatorname{det}\left(\begin{array}{ccc}
u_{1} & v_{1} & \hat{e}^{(1)} \\
u_{2} & v_{2} & \hat{e}^{(2)} \\
u_{3} & v_{3} & \hat{e}^{(3)}
\end{array}\right), \quad \text { or det }\left(\begin{array}{ccc}
u_{1} & u_{2} & u_{3} \\
v_{1} & v_{2} & v_{3} \\
e^{(1)} & \hat{e}^{(2)} & \hat{e}^{(3)}
\end{array}\right).\label{eqn:8} \]
This construct makes no sense as a matrix, because three of its elements are vectors. That is ok; it is just a device that allows us to compute the cross product using a pattern we have already memorized. We now calculate the determinant using the method of cofactors, expanding along the row or column that contains the unit vectors:
\[\vec{u} \times \vec{v}=\hat{e}^{(1)}\left(u_{2} v_{3}-u_{3} v_{2}\right)-\hat{e}^{(2)}\left(u_{1} v_{3}-u_{3} v_{1}\right)+\hat{e}^{(3)}\left(u_{1} v_{2}-u_{2} v_{1}\right) \nonumber \]
(cf. Equation 4.1.10).
Geometrical meaning of the determinant
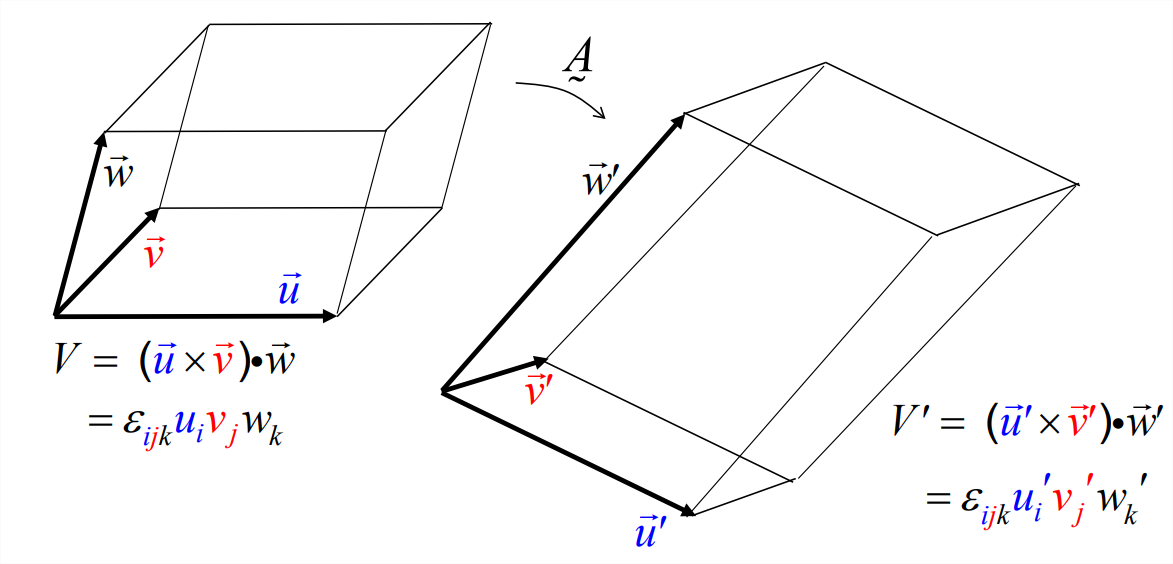
Consider the volume \(V\) of the parallelepiped formed by three arbitrary vectors \(\vec{u}\), \(\vec{v}\) and \(\vec{w}\) (Figure \(\PageIndex{3}\)). Assume for now that \(\vec{u}\), \(\vec{v}\) and \(\vec{w}\) form a right-handed triple, so that their triple product is positive. In that case, the triple product is equal to \(V\). Now suppose that the three vectors are transformed by the same matrix \(\underset{\sim}{A}\):
\[u_{i}^{\prime}=A_{i j} u_{j} ; \quad v_{i}^{\prime}=A_{i j} v_{j} ; \quad w_{i}^{\prime}=A_{i j} w_{j}. \nonumber \]
The volume of the new parallelepiped is
\[\begin{aligned} V^{\prime} &=\varepsilon_{i j k} u_{i}^{\prime} v_{j}^{\prime} w_{k}^{\prime} \\&=\varepsilon_{i j k} A_{i l} u_{l} A_{j m} v_{m} A_{k n} w_{n}\\&= \varepsilon_{i j k} A_{i l} A_{j m} A_{k n} u_{l} v_{m} w_{n}\quad\text{(reordering)}\\&= B_{l m n} u_{l} v_{m} w_{n}\end{aligned} \nonumber \]
where we have defined a new three-dimensional array \(B_{lmn} = \varepsilon_{ijk}A_{il}A_{jm}A_{kn}\).
Now we explore the meaning of \(\underset{\sim}{B}\). \(B_{lmn}\) is the triple product of columns \(l\), \(m\) and \(n\), where \(l\), \(m\) and \(n\) can be any integers 1, 2 or 3. In the special case \(lmn = 123\), \(B_{123}\) is just the determinant of \(\underset{\sim}{A}\) (cf. \(\PageIndex{4}\)). But what is \(\underset{\sim}{B}\) for arbitrary \(lmn\)? This situation is familiar; the triple product of three arbitrary vectors \(\vec{u}^{(i)}\), \(\vec{u}^{(j)}\) and \(\vec{u}^{(k)}\) is:
\[\left(\vec{u}^{(i)} \times \vec{u}^{(j)}\right) \cdot \vec{u}^{(k)}=T \varepsilon_{i j k}, \nonumber \]
where \(T = (\vec{u}^{(1)} \times \vec{u}^{(2)} )\cdot \vec{u}^{(3)}\) (cf. Equation \(\ref{eqn:3}\)). By the same reasoning,
\[B_{l m n}=\operatorname{det}(\underset{\sim}{A}) \varepsilon_{l m n}. \nonumber \]
Assembling these results, we find that \(V^\prime\) is \(|\underset{\sim}{A}|\) times the triple product of the original vectors \(\vec{u}\), \(\vec{v}\) and \(\vec{w}\). Equivalently,
\[V^{\prime}=\operatorname{det}(\underset{\sim}{A}) V.\label{eqn:9} \]
This is our geometrical interpretation of \(\operatorname{det}(\underset{\sim}{A})\): it is the factor by which the volume of the parallelepiped changes after transformation by \(\underset{\sim}{A}\). This interpretation also works for left-handed triples. But, if \(\operatorname{det}(\underset{\sim}{A})\) < 0, a right-handed triple will be converted into a left-handed triple, and vice versa.
Incidentally, this tells us something interesting about matrix transformations in general. You can transform any three vectors by the same matrix, and the parallelepiped they form will always expand by the same factor! Therefore, you can think of a matrix transformation as expanding all of space by a uniform factor.
Further properties of the determinant
Having identified the determinant as an expansion factor, we can now understand more of its properties.
- The determinant of a 2nd-order tensor is a scalar, clearly, because the expansion factor is invariant to rotations. If you double the volume of a parallelipped in one coordinate frame, you double it in all coordinate frames.
- The product rule says that the determinant of the product of two matrices is the product of the determinants. This can be understood by considering two successive transformations. Let us say a vector \(\vec{v}\) is transformed by the matrix \(\underset{\sim}{B}\), and then the result is transformed by the matrix \(\underset{\sim}{A}\). This can also be expressed as a single transformation by the product \(\underset{\sim}{A}\underset{\sim}{B}\). The net expansion has to be the same, whether you impose the expansions sequentially or together. For example, suppose that in successive transformations by the two matrices, you expand by a factor 2 and then by a factor 3, so the net expansion is 2\(\times\)3=6. When you apply the two transformations together, the expansion factor must also be 6.
- The inverse rule states that the determinant of the inverse is the inverse of the determinant. The inverse matrix reverses the initial transformation, giving you back your original vectors. So the net expansion factor, which is the product of the expansion factors for \(\underset{\sim}{A}\) and \(\underset{\sim}{A}^{-1}\), must be one.
- How about the fact that a matrix with zero determinant has no inverse? Well if \(\underset{\sim}{A}\) flattens all vectors onto the same plane, then that transformation is not reversible. This corresponds to the fact that \(\underset{\sim}{A}^{-1}\) doesn’t exist.
- In section 3.1.3 it was stated without proof that the determinant of an orthogonal matrix, i.e., a matrix whose inverse equals its transpose, is \(\pm\)1. We can now see why that is true. The determinant of the inverse equals the determinant of the transpose, which we know from property 1 is the same as the determinant of the original matrix. Therefore \(\operatorname{det}(\underset{\sim}{A})\) is a number that equals its own reciprocal. The only two such numbers are +1 and -1. Therefore, every orthogonal matrix is a rotation matrix. Those with determinant -1 change the sign of the volume of the parallelepiped, effectively turning it inside-out: improper rotations. Orthogonal matrices with determinant +1 represent proper rotations.
1This definition does not require that the columns actually transform as vectors; in general they do not.

