1.3: Liquid-liquid Extraction
- Page ID
- 76360
Staged Liquid-Liquid Extraction and Hunter Nash Method
\(E_n\) = extract leaving stage \(n\). This could refer to the mass of the stream or the composition of the stream.
\(F\) = solvent entering extractor stage 1. This could refer to the mass of the stream or the composition of the stream.
\(n\) = generic stage number
\(N\) = Final stage. This is where the fresh solvent S enters the system and the final raffinate \(R_N\) leaves the system.
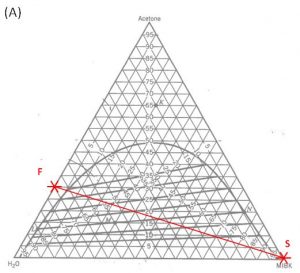
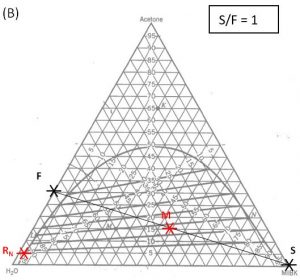
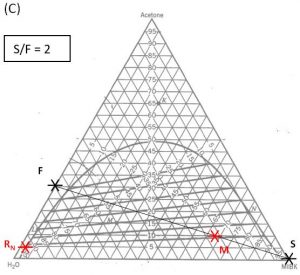
\(M\) = Composition of the mixture representing the overall system. Points (\(F\) and \(S\)) and (\(E_1\) and \(R_N\)) must be connected by a straight line that passes through point \(M\). \(M\) will be located within the ternary phase diagram.
\(P\) = Operating point. \(P\) is determined by the intersection of the straight line connecting points (\(F\), \(E_1\)) and the straight line connecting points (\(S\), \(R_N\)). Every pair of passing streams must be connected by a straight line that passes through point \(P\). \(P\) is expected to be located outside of the ternary phase diagram.
\(R_n\) = raffinate leaving stage \(n\). This could refer to the mass of the stream or the composition of the stream.
\(S\) = solvent entering extractor stage \(N\). This could refer to the mass of the stream or the composition of the stream.
\(S/F\) = mass ratio of solvent to feed
\((x_i)_n\) = Mass fraction of species \(i\) in the raffinate leaving stage \(n\)
\((y_i)_n\) = Mass fraction of species \(i\) in the extract leaving stage \(n\)
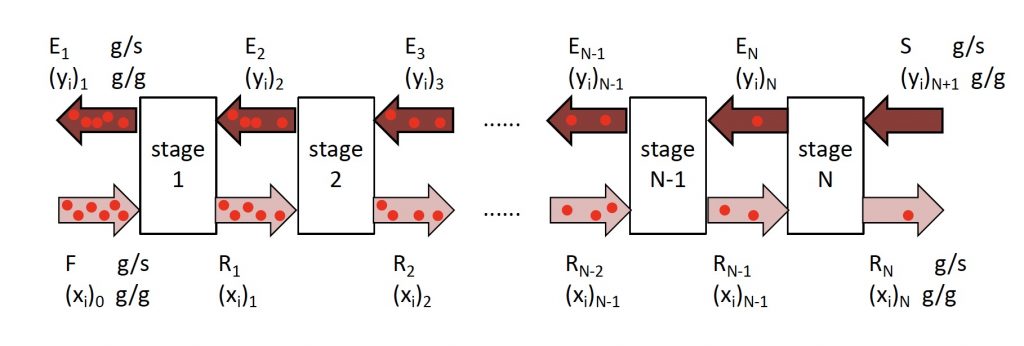
Process schematic for multistage liquid-liquid extraction.
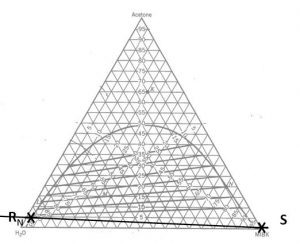
Determining number of stages \(N\) when (1) feed rate; (2) feed composition; (3) incoming solvent rate; (4) incoming solvent composition; and (5) outgoing raffinate composition have been specified/selected.
- Locate points \(F\) and \(S\) on the ternary phase diagram. Connect with a straight line.
- Do a material balance to find the composition of one species in the overall mixture. Use this composition to locate point \(M\) along the straight line connection points \(F\) and \(S\). Note the position of point \(M\).
- Locate point \(R_N\) on the ternary phase diagram. It will be on the equilibrium curve. Draw a straight line from \(R_N\) to \(M\) and extend to find the location of \(E_1\) on the equilibrium curve.
- On a fresh copy of the graph, with plenty of blank space on each side of the diagram, note the location of points \(F\), \(S\), and \(R_N\) (specified/selected) and \(E_1\) (determined in step 3).
- Draw a straight line between \(F\) and \(E_1\). Extend to both sides of the diagram. Draw a second straight line between \(S\) and \(R_N\). Note the intersection of these two lines and label as “\(P\)”.
- Determine the number of equilibrium stages required to achieve the desired separation with the selected solvent mass.
– Stream \(R_N\) is in equilibrium with stream \(E_N\). Follow the tie-lines from point \(R_N\) to \(E_N\).
– Stream \(E_N\) passes stream \(R_{N-1}\). Connect point \(E_N\) to operating point \(P\) with a straight line, mark the location of \(R_{N-1}\).
– Stream \(R_{N-1}\) is in equilibrium with stream \(E_{N-1}\). Follow the tie-lines from stream \(R_{N-1}\) to \(E_{N-1}\).
– Stream \(E_{N-1}\) passes stream \(R_{N-2}\). Connect \(E_{N-1}\) to operating point \(P\) with a straight line, mark the location of \(R_{N-2}\).
– Continue in this manner until the extract composition has reached or passed \(E_{1}\). Count the number of equilibrium stages.
Watch this two-part series of videos from LearnChemE that shows how to use the Hunter Nash method to find the number of equilibrium stages required for a liquid-liquid extraction process.
- Hunter Nash Method 1: Mixing and Operating Points (9:30)
- Hunter Nash Method 2: Number of Stages (6:30)
1000 kg/hr of a feed containing 30 wt% acetone, 70 wt% water. The solvent is pure MIBK. We intend that the raffinate contain no more than 5.0 wt% acetone. How many stages will be required for each proposed solvent to feed ratio in the table below?
| \(\textbf{S/F}\) | \(\textbf{S}\) (kg/hr) | \(\textbf{(x_A)_M}\) | target \(\textbf{(y_A)_1}\) | \(\textbf{N}\) |
| 1.0 | ||||
| 2.0 | ||||
| 0.2 |


Hunter Nash Method for Finding Smin, Tank Sizing and Power Consumption for Mixer-Settler Units
Staged LLE: Hunter-Nash Method for Finding the Minimum Solvent to Feed Ratio
\(E_n\) = extract leaving stage \(n\). This could refer to the mass of the stream or the composition of the stream.
\(F\) = solvent entering extractor stage 1. This could refer to the mass of the stream or the composition of the stream.
\(n\) = generic stage number
\(N\) = Final stage. This is where the fresh solvent \(S\) enters the system and the final raffinate \(R_N\) leaves the system.
\(M\) = Composition of the overall mixture. Points (\(F\) and \(S\)) and (\(E_1\) and \(R_N\)) are connected by a straight line passing through \(M\).
\(P\) = Operating point. Every pair of passing streams must be connected by a straight line that passes through \(P\).
\(R_n\) = raffinate leaving stage \(n\). This could refer to the mass of the stream or the composition of the stream.
\(S\) = solvent entering extractor stage \(N\). This could refer to the mass of the stream or the composition of the stream.
\(S/F\) = mass ratio of solvent to feed
\(S_{\rm min}/F\) = Minimum feasible mass ratio to achieve the desired separation, assuming the use of an infinite number of stages.
\((x_i)_n\) = Mass fraction of species \(i\) in the raffinate leaving stage \(n\)
\((y_i)_n\) = Mass fraction of species \(i\) in the extract leaving stage \(n\)
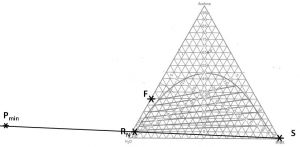
\(P_{\rm min}\) = Point associated with the minimum feasible \(S/F\) for this feed, solvent and (raffinate or extract) composition. \(P_{\rm min}\) is the intersection of the line connecting points (\(R_N\), \(S\)) and the line that is an extension of the upper-most equilibrium tie-line.
Determining minimum feasible solvent mass ratio (\(S_{\rm min}/F\)) when (1) feed composition; (2) incoming solvent composition; and (3) outgoing raffinate composition have been specified/selected.
- Locate points \(S\) and \(R_N\) on the phase diagram. Connect with a straight line.
- Extend the upper-most tie-line in a line that connects with the line connecting points (\(S\) and \(R_N\)). Label the intersection \(P_{\rm min}\).
- Find point \(F\) on the diagram. Draw a line from \(P_{\rm min}\) to F and extend to the other side of the equilibrium curve. Label \(E_1\)@\(S_{\rm min}\).
- On a fresh copy of the phase diagram, label points \(F\), \(S\), \(R_N\) and \(E_1\)@\(S_{\rm min}\). Draw one line connecting points \(S\) and \(F\) and another line connecting points \(E_1\)@\(S_{\rm min}\)
- and \(R_N\). The intersection of these two lines is mixing point \(M\). Note the composition of species \(i\) at this location.
- Calculate
\[\dfrac{S_{\rm min}}{F} = \dfrac{(x_i)_F - (x_i)_M}{(x_i)_M - (x_i)_S} \tag{5.1}\]
We have a 1000 kg/hr feed that contains 30 wt% acetone and 70 wt% water. We want our raffinate to contain no more than 5.0 wt% acetone. What is the minimum mass of pure MIBK required?
Liquid-Liquid Extraction: Sizing Mixer-settler Units
\(\Phi_C\) = volume fraction occupied by the continuous phase
\(\Phi_D\) = volume fraction occupied by the dispersed phase
\(\mu_C\) = viscosity of the continuous phase (mass time-1 length-1)
\(\mu_D\) = viscosity of the dispersed phase (mass time-1 length-1)
\(\mu_M\) = viscosity of the mixture (mass time-1 length-1)
\(\rho_C\) = density of the continuous phase (mass volume-1)
\(\rho_D\) = density of the dispersed phase (mass volume-1)
\(\rho_M\) = average density of the mixture (mass volume-1)
\(D_i\) = impeller diameter (length)
\(D_T\) = vessel diameter (length)
\(H\) = total height of mixer unit (length)
\(N\) = rate of impeller rotation (time-1)
\(N_{\rm Po}\) = impeller power number, read from Fig 8-36 or Perry’s 15-54 (below) based on value of \(N_{Re}\) (unitless)
\((N_{\rm Re})_C\) = Reynold’s number in the continuous phase = inertial force/viscous force (unitless)
\(P\) = agitator power (energy time-1)
\(Q_C\) = volumetric flowrate, continuous phase (volume time-1)
\(Q_D\) = volumetric flowrate, dispersed phase (volume time-1)
\(V\) = vessel volume (volume)
Tank and impeller sizing
\[\rm residence time = \dfrac{V}{Q_C + Q_D} \tag{5.2}\]
Geometry of a cylinder
\[V = \dfrac{\pi D_T^2H}{4} \tag{5.3}\]
General guidelines
\[\dfrac{H}{D_T} = 1 \tag{5.4}\]
\[\dfrac{D_i}{D_T} = \dfrac{1}{3} \tag{5.5}\]
Impeller power consumption:
\[P=N_{Po}N^3D_i^5{\rho}_m \tag{5.6}\]
\[N_{Re}=\frac{D_i^2N{\rho}_M}{{\mu}_M} \tag{5.7}\]
\[{\rho}_M={\rho}_C{\Phi}_C+{\rho}_D{\Phi}_D \tag{5.8}\]
\[{\mu}_M=\frac{{\mu}_C}{{\Phi}_C}\left[1+\frac{1.5{\mu}_D{\Phi}_D}{{\mu}_C+{\mu}_D}\right] \tag{5.9}\]
Modeling Mass Transfer in Mixer-Settler Units
\(\Delta\rho\) = density difference (absolute value) between the continuous and dispersed phases (mass volume-1)
\(\phi_C\) = volume fraction occupied by the continuous phase
\(\phi_D\) = volume fraction occupied by the dispersed phase
\(\mu_C\) = viscosity of the continuous phase (mass time-1 length-1)
\(\mu_D\) = viscosity of the dispersed phase (mass time-1 length-1)
\(\mu_M\) = viscosity of the mixture (mass time-1 length-1)
\(\rho_C\) = density of the continuous phase (mass volume-1)
\(\rho_D\) = density of the dispersed phase (mass volume-1)
\(\rho_M\) = average density of the mixture (mass volume-1)
\(\sigma\) = interfacial tension between the continuous and dispersed phases
(mass time-2)
\(a\) = interfacial area between the two phases per unit volume (area volume-1)
\(c_{D,\rm in}\), \(c_{D,\rm out}\) = concentration of solute in the incoming or outgoing dispersed streams (mass volume-1)
\(c^*_D\) = concentration of solute in the dispersed phase if in equilibrium with the outgoing continuous phase (mass volume-1)
\(D_C\) = diffusivity of the solute in the continuous phase (area time-1)
\(D_D\) = diffusivity of the solute in the dispersed phase (area time-1)
\(D_i\) = impeller diameter (length)
\(D_T\) = vessel diameter (length)
\(d_{vs}\) = Sauter mean droplet diameter; actual drop size expected to range from \(0.3d_{vs}-3.0d_{vs}\) (length)
\(E_{MD}\) = Murphree dispersed-phase efficiency for extraction
\(g\) = gravitational constant (length time-2)
\(H\) = total height of mixer unit (length)
\(k_c\) = mass transfer coefficient of the solute in the continuous phase (length time-1)
\(k_D\) = mass transfer coefficient of the solute in the dispersed phase (length time-1)
\(K_{OD}\) = overall mass transfer coefficient, given on the basis of the dispersed phase (length time-1)
\(m\) = distribution coefficient of the solute, \(\Delta c_C/\Delta c_D\) (unitless)
\(N\) = rate of impeller rotation (time-1)
\((N_{\rm Eo})_C\) = Eotvos number = gravitational force/surface tension force (unitless)
\((N_{\rm Fr})_C\) = Froude number in the continuous phase = inertial force/gravitational force (unitless)
\(N_{\rm min}\) = minimum impeller rotation rate required for complete dispersion of one liquid into another
\((N_{\rm Re})_C\) = Reynold’s number in the continuous phase = inertial force/viscous force (unitless)
\((N_{\rm Sh})_C\) = Sherwood number in the continuous phase = mass transfer rate/diffusion rate (unitless)
\((N_{\rm Sc})_C\) = Schmidt number in the continuous phase = momentum/mass diffusivity (unitless)
\((N_{\rm We})_C\) = Weber number = inertial force/surface tension (unitless)
\(Q_D\) = volumetric flowrate of the dispersed phase (volume time-1)
\(V\) = vessel volume (volume)
Calculating \(N_{\rm min}\)
\[\dfrac{N_{\rm min}^2 \rho_M D_i}{g \Delta \rho} = 1.03 \left(\dfrac{D_T}{D_i}\right)^{2.76} (\phi_D)^{0.106} \left(\dfrac{\mu_M^2 \sigma}{D_i^5 \rho_M g^2 (\Delta \rho)^2} \right)^{0.084} \tag{6.1}\]
\[{\rho}_M={\rho}_C{\phi}_C+{\rho}_D{\phi}_D \tag{6.2}\]
\[{\mu}_M=\frac{{\mu}_C}{{\phi}_C}\left(1+\frac{1.5{\mu}_D{\phi}_D}{{\mu}_C+{\mu}_D}\right) \tag{6.3}\]
Estimating Murphree efficiency for a proposed design
Sauter mean diameter
\[{\rm if}\;\; N_{\rm We} < 10,000,\; d_{vs}=0.052D_i(N_{\rm We})^{-0.6}\exp({4{\phi}_D}) \tag{6.4}\]
\[{\rm if}\;\; N_{\rm We} >10,000,\; d_{vs}=0.39D_i(N_{\rm We})^{-0.6} \tag{6.5}\]
\[N_{\rm We}=\frac{D_i^3N^2{\rho}_C}{\sigma} \tag{6.6}\]
mass transfer coefficient of the solute in each phase
\[k_D=\frac{6.6D_D}{d_{vs}} \tag{6.7}\]
\[k_C=\frac{(N_{\rm Sh})_CD_c}{d_{vs}} \tag{6.8}\]
\[(N_{\rm Sh})_C = 1.237 \times 10^{-5} (N_{\rm Sc})_C^{1/3} (N_{\rm Re})_C^{2/3} (\phi_D)^{-1/2} \tag{6.9}\]
\[(N_{\rm Fr})_C^{5/12} \left( \dfrac{D_i}{d_{vs}} \right)^2 \left( \dfrac{d_{vs}}{D_T} \right)^{1/2} (N_{Eo})_C^{5/4} \tag{6.9} \]
\[(N_{\rm Sc})_C=\frac{{\mu}_C}{{\rho}_CD_C} \tag{6.10}\]
\[(N_{\rm Re})_C=\frac{D_i^2N{\rho}_C}{{\mu}_C} \tag{6.11}\]
\[(N_{\rm Fr})_C = \dfrac{D_i N^2}{g} \tag{6.12}\]
\[(N_{Eo})_C = \dfrac{\rho_D d_{vs}^2 g}{\sigma} \tag{6.13}\]
Overall mass transfer coefficient for the solute
\[\frac{1}{K_{OD}}=\frac{1}{k_D}+\frac{1}{mk_C} \tag{6.14}\]
Murphree efficiency
\[E_{MD}=\frac{K_{OD}aV}{Q_D}\left(1+{\frac{K_{OD}aV}{Q_D}}\right)^{-1} \tag{6.15}\]
\[a=\frac{6\phi_D}{d_{vs}} \tag{6.16}\]
Experimental assessment of efficiency
\[E_{MD}=\frac{c_{D,\rm in}-c_{D,\rm out}}{c_{D,\rm in}-c^*_D} \tag{6.17}\]
1000 kg/hr of 30 wt% acetone and 70 wt% water is to be extracted with 1000 kg/hr of pure MIBK. Assume that the extract is the continuous phase, a residence time of 5 minutes in the mixing vessel, standard sizing of the mixing vessel and impeller. Find the power consumption and Murphree efficiency if the system operates at \(N_{\rm min}\), controlled at the level of 1 rev/s. Ignore the contribution of the solute and the co-solvent to the physical properties of each phase.
- MIBK
- density = 802 kg m-3
- viscosity = 0.58 cP
- diffusivity with acetone at 25°C = 2.90×10-9 m2 s-1
- Water
- density = 1000 kg m-3
- viscosity = 0.895 cP
- diffusivity with acetone at 25°C = 1.16×10-9 m2 s-1
- The interfacial tension of water and MIBK at 25°C = 0.0157 kg s-2. Use the ternary phase diagram to find \(m\).
Liquid-Liquid Extraction Columns
\(\Delta \rho\) = density difference (absolute value) between the continuous and dispersed phases (mass volume-1)
\(\mu_C\) = viscosity of the continuous phase (mass time-1 length-1)
\(\rho_C\) = density of the continuous phase (mass volume-1)
\(\rho_D\) = density of the dispersed phase (mass volume-1)
\(\sigma\) = interfacial tension between the continuous and dispersed phases
(mass time-2)
\(D_T\) = column diameter (length)
\(H\) = total height of column (length)
\({\rm HETS}\) = height of equilibrium transfer stage (length)
\(m^*_C\) = mass flowrate of the entering continuous phase (mass time-1)
\(m^*_D\) = mass flowrate of the entering dispersed phase (mass time-1)
\(N\) = required number of equilibrium stages
\(u_0\) = characteristic rise velocity of a droplet of the dispersed phase (length time-1)
\(U_i\) = superficial velocity of phase \(i\) (C = continuous, downward; D = dispersed, upward) (length time-1)
\(V^*_i\) = volumetric flowrate of phase \(i\) (volume time-1)
\[U_i = \dfrac{4V_i^*}{\pi D_T^2} \tag{7.1}\]
definition of superficial velocity
\[\dfrac{U_D}{U_C} = \dfrac{m_D^*}{m_C^*} \left( \dfrac{\rho_C}{\rho_D} \right) \tag{7.2}\]
\[(U_D + U_C)_{\rm actual} = 0.50(U_D + U_C)_f \tag{7.3}\]
for operation at 50% of flooding
\[u_0 = \dfrac{0.01 \sigma \Delta \rho}{\mu_C \rho_C} \tag{7.4} \]
for rotating-disk columns, \(D_T\) = 8 to 42 inches, with one aqueous phase
\[D_T = \left( \dfrac{4m_D^*}{\rho_D U_D \pi} \right)^{0.5} = \left( \dfrac{4m_C^*}{\rho_C U_C \pi} \right)^{0.5} \tag{7.5}\]
\[H = \rm HETS * N \tag{7.6}\]
1000 kg/hr of 30 wt% acetone and 70 wt% water is to be extracted with 1000 kg/hr of pure MIBK in a 2-stage column process. Assume that the extract is the dispersed phase. Ignoring the contribution of the solute and the co-solvent to the physical properties of each phase, find the required column diameter and height.
- MIBK
- density = 802 kg m-3
- viscosity = 0.58 cP
- Water
- density = 1000 kg m-3
- viscosity = 0.895 cP
- The interfacial tension of water and MIBK at 25°C = 0.0157 kg s-2.


