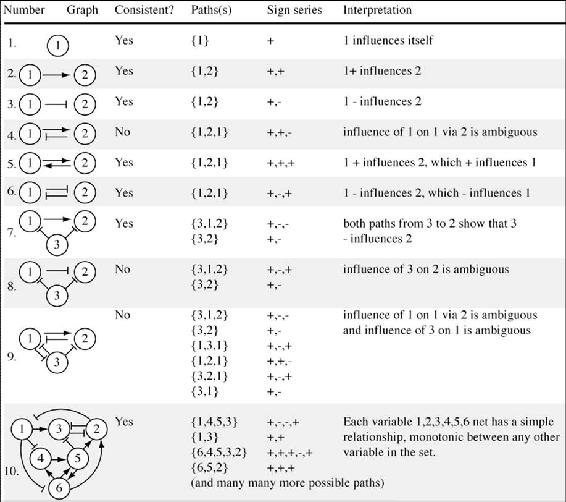
2.3: Incidence Graphs -Interpretations, Consistency, and Inconsistency
- Page ID
- 22366
3.1 Introduction
Incidence graphs are useful tools for chemical engineers to model various relationships in a process. They are used to systematically map an entire chain of processes and controllers to describe the effect, which each element has on the others. This helps to visualize the possible process pathways or a chain of effects.
Below is an example of an incidence graph. The circles are nodes which represent a particular device or controller, e.g. a temperature sensor. The arrows indicate the directional pathway of influence. For instance, a temperature sensor node would be connected to an adjacent node (such as a heat exchanger). This heat exchanger node would in turn be connected to other nodes representing devices or controllers. This type of diagram could be extremely useful in identifying the redundancies within a control system. A more elaborate application of incidence graphs will be discussed in the Worked Out Examples section.
Monotonicity
Before proceeding to the next few sections, it is imperative to understand the basics of monotone systems. A monotonic function defines a function that preserves a given order. Monotonic functions are classified as monotonic increasing or monotonic decreasing. Taking the example of a function f(x), for a monotonic increasing function an increase in variable ‘x’ would result in an increase in f(x). On the other hand, for a monotonic decreasing function an increase in variable ‘x’ would result in a decrease in f(x).
Monotonic Increase : If x≥y, then f(x)≥f(y) 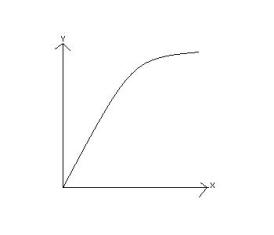
Monotonic Decrease : If x≥y, then f(x)≤f(y) 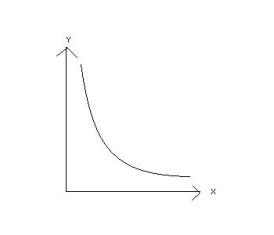
As long as a function is either always monotone increasing or monotone decreasing, it is referred to as a monotone function.
Monotonic functions are ideal systems to control because changes in one variable/device lead to known changes in other variables/devices. A non-monotonic function on the other hand, does not yield a straightforward output for a particular input. In these cases IF-THEN-ELSE statements are used to illustrate the controls for the nodes. For instances, IF node 1 is activated, THEN node 2 is repressed and so on.
An example of a possible non-monotonic graph 
Incidence Graphs
Incidence graphs (also “Levi” or “Causation” graphs) consist of monotonic connections between nodes, whereby each connection indicates a particular effect of one factor on another. The term “monotonic” means that a change in the initiating device influences only one aspect of the target device. This simplification facilitates describing how control systems work through the use of incidence diagrams.
In reality, not all interactions are monotonic. Some control devices can simultaneously affect several aspects of other devices or variables. This may result in a non-monotonic relationship, in which one factor increases another over one region, but diminishes it over another (imagine a parabola, which is a non-monotonic curve). Temperature often has such a relationship with the rate of a reaction: for an exothermic reversible reaction, increasing the temperature will increase yield up to a certain point; however, further increase will diminish the yield.
Incidence graphs can only be used to represent monotonic relationships. Therefore, over simplification of a system can cause problems in constructing an incidence graph. Similarly a non-monotonic relationship can be resolved by breaking down a factor into separate components, each of which has only monotonic relationships with other factors.
When two factors are connected by multiple signal paths, incoherence between the results of different paths leads to inconsistency. In other words, the outcome cannot be predicted because the incidence graph does not communicate quantitative information. For instance, in the reaction rate example, reaction rate could be separated into the variables which affect it: concentrations, rate constant, and equilibrium constant. An incidence graph can then be constructed to demonstrate that temperature and reaction rate have an inconsistent relationship.
A diagram is consistent (to be discussed later in detail) if all signal paths between two nodes, for every pair of nodes, are in agreement with one another (i.e. they have the same result).
Traversing
Every incidence graph establishes a particular way to depict the direct effects of one device on its neighbors. Typically, a line will connect a node to its neighbors--these lines are terminated by either a bar or an arrowhead.
An arrowhead at the end indicates that the initiator (from which the line is coming) is either increasing the value of the target (where the arrow is pointing) or simply activating it (turning it on). The context of the connection will determine whether something is being increased or turned on. For example, it would be illogical to assume that a drop in temperature would cause a temperature controller to deactivate a pressure controller. Instead, it would be more prudent to assume that the temperature controller would adjust the pressure sensor.

arrowhead bar
A perpendicular bar indicates that the initiating device is either decreasing the value of the target device or inhibiting it (turn off). Note that these indications are not necessarily strictly followed. Once again, context of the situation determines which interpretation should be used.

perpendicular bar
Graphs consisted of the arrowhead bar and the perpendicular bar allow you to see the result of an increase/decrease in one aspect of the initial device on a designated device in the system. Everything done after the initial device comes as a result of changing the initial device. In addition, these graphs provide the possibility of simplifying complicated relationships between devices into one conceptual unit. The relationship between the initiating device and target nodes can be described by the following set --> {initiator,target1,target2,etc}. It is read as "the increase or decrease in the initiating device affects the target nodes in the following manner... (+ for increase/activate and - for decrease/inhibit). The initiator can be any device or variable in the system as long as the arrows support the designation. In other words, you can show the effects of any device on any other device, as long as the pathway is supported by the diagram. There are often multiple routes that a signal can travel.
2 helpful tips to keep in mind as you interpret an incidence graph:
1. Always travel from tail to head (or source to target) when traversing the graph from the initiating device to the designated device. Keep in mind that it is possible to have arrowhead and/or perpendicular bars pointing in both directions in between two devices.
2. Arrowhead bars don’t always mean increase as perpendicular bars don’t always mean decrease. Arrowhead bars indicate that the effect of performing an action to the device at the tail of the bar would yield the same effect to the device at the head of the bar. Penpendicular bars indicate that the effect of performing an action to the device at the tail of the bar would yield the reverse effect to the device at the head of the bar.
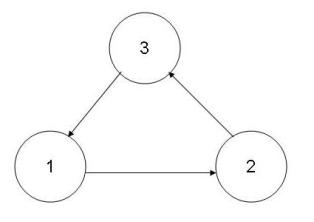
The following is a simple example of an incidence graph. We will refer to the circles below as “nodes” from this point onward. Nodes are the selected devices or variables in a control system.
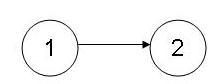
This incidence graph indicates that:
a. A change in an aspect of 1 will change some aspect of device 2 in the same direction -- otherwise written as {+,+}
The ends indicate the direction of influence as well as the type of influence.

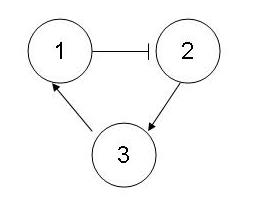
This incidence graph indicates that:
- increase in an aspect of 2 (initiator) decreases some aspect of 1 (target)
- indicated by {+,-}
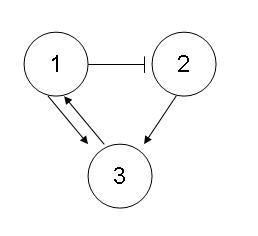
This next example builds on the previous two...
This incidence graph indicates that:
Given an arbitrary 3,1,2 order, an increase in 3 (initiator) will make 1 (target) go up. 1’s increase will then make 2 decrease. The symbolic representation for this would be {+,+,-}. One can see that this diagram shows how node 3 influences everything directly and indirectly connected to it.
Now, given a 1,2,3 order, node one becomes the initiator. The symbolic representation then changes to {+,-,-}. NOTE: the last node is negatively affected because 2’s impact on 3 is shown to increase when 2 increases. But since 1 decreases 2, then the opposite is true!
The main objective of these diagrams is to determine the effect that a change in the starting node has on another node in the system. However, in some cases, you can follow a pathway that ends at the starting node in order to check for ambiguity. For example, the 1,2,3,1 order yields a result of {+,-,-,-}. Since increasing node 1 cannot cause a decrease in itself, it is ambiguous.
Incidence graphs for complex controls systems will usually indicate that there are several ways for a device to influence another device in the system.
Multiple paths
Remember these are done with respect to increases in a node’s value. So, if a path leads you to a point where you decrease a node, then you have to do the opposite of what the diagram is indicating for all steps after that (for that route).
The incidence graph indicates:
1. For an order {1,2,3}: you observe {+,-,-}... remember not to count beginning node twice…
2. For an order {1,3}: you observe {+,+}
Consistent, Inconsistent, and Partially Consistent
When designing controls for systems it is always important to keep in mind the need for redundacy and feedback control. Redundancy in a system will ensure that a system is monitored by multiple controllers. So, if one controller was to fail there would be another to ensure the same desired outcome. Consistent graphs can be used to describe redundancy. Feedback control is also very important and it is not good to have the system overreact to external stimuli. A controlled response is desired. Inconsistent graphs can be used to describe feedback control. Additionally, systems exist that both need to be redundant and feedback controlled and these can be described with partially consistent graphs.
Consistent Graphs
Consistent pathways happen when all pathways from the same starting node, that lead to the same target node, give the same output.
For example,
All possible pathways from node 1 to target node 4 yield the same output. These are called consistent pathways.
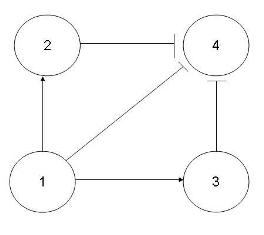
| Paths(s) | Sign series |
| 1,4 | (+,-) |
| 1,2,4 | (+,+,-) |
| 1,3,4 | (+,+,-) |
From the table and graph above, all pathways from node 1 to node 4 yield the same outcome. Node 4 is being decreased.
A consistent graph is made up of only consistent pathways for all possible pathways between any combination of two nodes. The graph below is an example of a consistent graph.
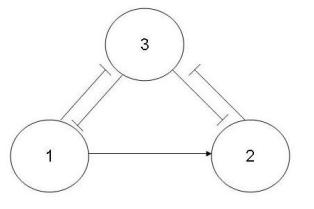
| Paths(s) | Sign series |
| 1,2,3 | (+,+,-) |
| 1,3 | (+,-) |
| 3,1,2 | (+,-,-) |
| 3,2 | (+,-) |
| 1,3,1 | (+,-,+) |
| 1,2,3,1 | (+,+,-,+) |
| 3,2,3 | (+,-,+) |
| 3,1,3 | (+,-,+) |
| 3,1,2,3 | (+,-,-,+) |
All pathways leading from node 1 to node 3 -
1,2,3 : (+,+,-)
1,3 : (+,-)
Since the two pathways cause the same change to node 3, this sub-pathway is consistent.
All pathways leading from node 3 and to node 2 -
3,1,2 : (+,-,-)
3,2 : (+,-)
Since the two pathways cause same change to node 2, this sub-pathway is consistent.
All pathways leading from node 1 and back to node 1 -
1,3,1 : (+,-,+)
1,2,3,1: (+,+,-,+)
Since the two pathways result in the same change to node 1, this sub-pathway is consistent.
All pathways leading from node 3 and back to node 3 -
3,2,3 : (+,-,+)
3,1,3 : (+,-,+)
3,1,2,3: (+,-,-,+)
Since the three pathways give the same effects to node 3, this sub-pathway is consistent.
Because all sub-pathways of this incidence graph are consistent, the entire process is consistent.
The table shown below gives examples of many different incidence diagrams and shows whether or not they are consistent.
Another type of consistent graph is one in which the valves of the system are not dependent on one another for feedback. In other words, there is no proportion of the output signal from a particular valve of a system is passed to the input of another valve. An example of this would be to consider the following process diagram:
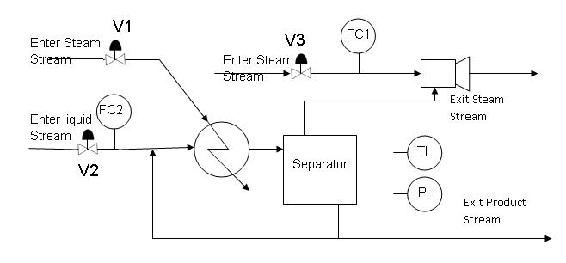
This process is of a distillation column in which the bottom columns collect high intensity liquids and the liquid is removed from a series of evaporators. The evaporator is a single-effect evaporator equipped with a simple heat exchanger, a separation vessel and a steam jet ejector to supply the vacuum. The product is then sent to an oven where it is dried and sent to the manufacturer. It is the chemical engineer’s task to create a consistent incidence graph in which the valves in the diagram do not depend on each other’s feedback. An example of this is below:

| Paths(s) | Sign series |
| V1, TI, PI, TI | (+,+,+,+) |
| V2, TI, PI, TI | (+,-,-,-) |
| V3, PI, TI, PI | (+,-,-,-) |
Based on the table above, the incidence graph is consistent because the valves are not dependent on one another for feedback.
Inconsistent Graphs
Inconsistent pathways happen when pathways from the same starting node, that lead to the same target node, give different output.
For example,
Pathways from node 1 to target node 4 do not yield the same output. These are called inconsistent pathways.

| Paths(s) | Sign series |
| 1,4 | (+,+) |
| 1,2,4 | (+,+,-) |
| 1,3,4 | (+,-,+) |
From the table and graph above, all pathways from node 1 to node 4 do not yield the same outcome. Node 4 is being decreased while simultaneously being increased.
An inconsistent graph is made up of only inconsistent pathways for all possible pathways between any combinations of two nodes. The graph below is an example of an inconsistent graph.
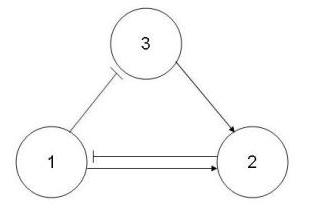
| Paths(s) | Sign series |
| 1,2 | (+,+) |
| 1,3,2 | (+,-,-) |
| 1,2,1 | (+,+,-) |
| 1,3,2,1 | (+,-,-,+) |
All pathways leading from node 1 to node 2 -
1,2 : (+,+)
1,3,2 : (+,-,-)
Since the two pathways cause different changes to node 2, this sub-pathway is inconsistent.
All pathways leading from node 1 and back to node 1 -
1,2,1 : (+,+,-)
1,3,2,1: (+,-,-,+)
Since the two pathways cause different changes to node 1, this sub-pathway is inconsistent.
Because all sub-pathways in this incidence graph are inconsistent, the incidence graph is inconsistent.
Partially Consistent Graphs
Partially consistent graphs are made up of both consistent and inconsistent pathways. If you increase node 1, all paths leading to node 4 cause a decrease in the node which means it is a consistent pathway. If node 1 is increased, one path leading to node 2 causes an increase and another path causes a decrease in the node. This is an inconsistent pathway. Since this model contains both at least one consistent and one inconsistent pathway, it is a partially consistent model.
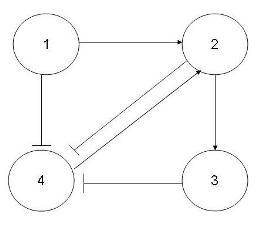
| Paths(s) | Sign series |
|---|---|
| 1,2,3,4 | (+,+,+,-) |
| 1,2,4 | (+,+,-) |
| 1,4 | (+,-) |
| 1,2 | (+,+) |
| 1,4,2 | (+,-,-) |
All pathways leading from node 1 to node 4 -
1,2,3,4: (+,+,+,-)
1,2,4 : (+,+,-)
1,4 : (+,-)
Since the three pathways cause the same change to node 4, this sub-pathway is consistent.
All pathways leading from node 1 and to node 2 -
1,2 : (+,+)
1,4,2 : (+,-,-)
Since the two pathways cause different changes to node 2, this sub-pathway is inconsistent.
In this graph there are sub-pathways that are consistent and inconsistent, therefore the incidence graph is partially consistent.
Summary
Just because a process is inconsistent does not mean that the desired results cannot be achieved. All it means is that you cannot consistently achieve the desired results. Take the example of the flow of a final product. In a consistent process, no matter which path is taken, the flow of the final product will always respond the same, whether desirable or not. In an inconsistent process, changing the path will not always cause the flow of the final product to change the same way, but rather depends on the path taken.
In all, inconsistent processes are not bad. Often, processes will be very complex, containing many variables, and inconsistent processes will be unavoidable. Care must just be taken with complex, inconsistent processes to achieve desirable results.
Worked out Example 1
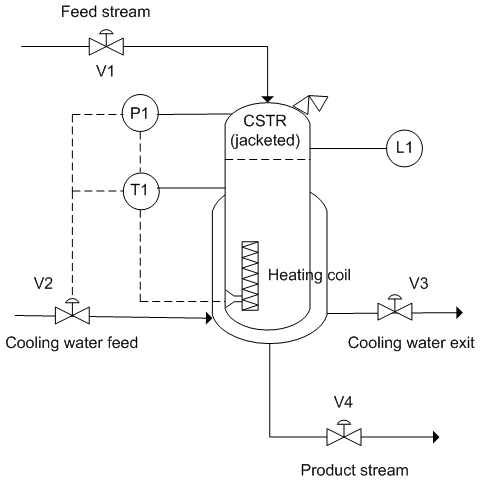
You are a process engineer and you have been assigned to devise a process control for a new reactor. The optimum operating condition for the reaction inside the reactor is 220 oC ± 10oC. The reaction is exothermic and often goes way past the optimum temperature. It is imperative that the reaction should not go above 250oC. The reactor has a built in heater (H1) to keep temperature at its optimum temperature and a cooling water feed to cool the reactor in case temperature goes past 250oC. The reactor also has temperature sensor installed to monitor the temperature. If temperature goes above 250oC, the desired mechanism is to increase the flow of water in the cooling jacket surrounding the reactor and to turn off the heating element inside the reactor until it reaches its optimum temperature. As a control redundancy mechanism, a pressure sensor is also installed inside the reactor. The pressure control will send signal to the cold water feed if pressure reaches 1.2 atm which is the critical pressure. Draw a causation graph governing the situation when the temperature gets too hot inside the reactor. Base your graph on the following variables:
Note: (There may be more than one correct solution to the assigned problem)
- temperature
- temperature sensor (T1)
- cooling water feed (V3)
- heating element (H1)
- pressure
- pressure sensor (P1)
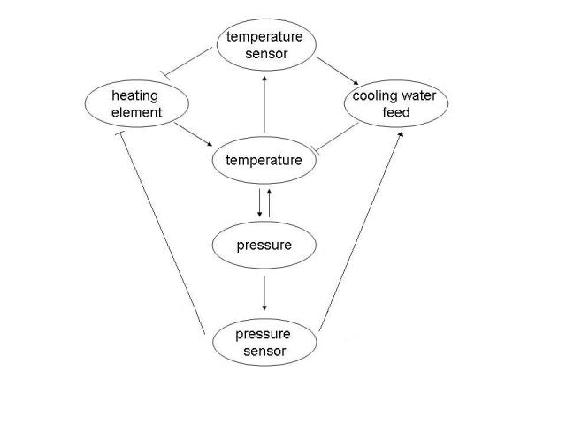
High temperature will 'activate' the temperature sensor, telling it that the temperature has exceeded the optimal temperature and an action need to be done to bring it back to the desired temperature. The temperature sensor would then open the valve for the cooling water feed which would cause the water to flow through the jacket. This results in the temperature inside the reactor to decrease. The reverse happens for the heating element. An activation of the temperature sensor would translate to an inhibition of the heating element in which the heating element would stop increasing the temperature of the reactor. Temperature and pressure are directly related by ideal gas law and thus affects each other in both ways. Thus, for the control redundancy mechanism, an increase in pressure would activate the pressure sensor which would then activate the cooling water feed to cool the temperature for the reactor.
Logic control:
- IF T1 =< 220 oC, THEN H1 is on, ELSE H1 is off
- IF T1 >= 250 oC, THEN V2 and V3 is open, ELSE V2 and V3 is close
- IF P1 >= 1.2 atm, THEN V2 and V3 is open, ELSE V2 and V3 is close
Worked out Example 2
After completing the assignment of devising the temperature control, your boss asked you to devise a mechanism to control the flow of raw materials and products. Draw a causation graph showing negative feedback relations between L1, V1 and V4 when the level inside the reactor is increasing (this is an example of an inconsistent pathway). The normal operating conditions are shown below:
V1 is 50 gal/min, V1 is usually open
V4 is 50 gal/min, V4 is usually open
L1 is 20 meters, L1 should not go above 30 meters and should not be below 10 meters
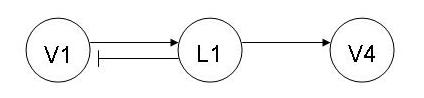
The level sensor monitors the fluid height inside the jacketed CSTR. Assuming the level inside the reactor is increasing steadily, the level sensor will send a negative feedback signal to V1 to decrease the input flow.
Logic control:
IF L1 > 30 meters, THEN V1 is closed
IF L1 < 10 meters, THEN V4 is closed
Worked out Example 3
Determine whether the following causation graph is consistent, inconsistent or partially consistent. Include your reasoning.
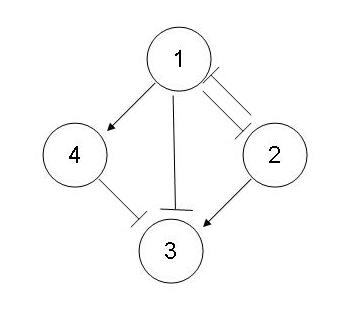
Solution:
All relationships are consistent. Each variable 1,2,3,4 has a simple relationship which is monotonic among the other variables in the set.
| Paths(s) | Sign series |
|---|---|
| {1,2} | (+,-) |
| {1,2,3} | (+,-,-) |
| {1,3} | (+,-) |
| {1,4,3} | (+,+,-) |
| {1,4} | (+,+) |
| {2,1} | (+,-) |
| {2,3} | (+,+) |
| {2,1,3} | (+,-,+) |
| {2,1,4} | (+,-,-) |
| {4,3} | (+,-) |
References
- Woolf, Peter (2006). A Mini-Guide to Consistent Graphs.
- Woolf, Peter (2006). Terms Review.
- Angeli, David & Sontag, Eduardo D. (2003). Monotone Control Systems.
Contributors and Attributions
- Authors: (September 26, 2006) Christopher Garcia, Anwar Stephens, Winardi Kusumaatmaja, Meng Yang Ng
- Stewards: (September 5, 2007) Alexander Voice, Andrew Wilkins, Ibrahim Oraiqat, Rohan Parambi


