6.6: ODE and Excel model of a Heat Exchanger
- Page ID
- 22396
Introduction
In process industries, heat exchangers are designed to transfer heat from one fluid to another. Heat exchangers have many different applications, especially in chemical processes, air conditioning, and refrigeration. They are classified by their design and type of flow. In some types of heat exchangers, the two fluids are separated by a wall or membrane and the heat transfer takes place by both convection and conduction. In another, less common type of exchanger, the two fluids physically come into contact with each other as the heat transfer occurs.
Since heat exchangers have a wide variety of applications and are commonly used in industry, control of the system is essential. A dynamic model may be created to allow the chemical engineer to optimize and control the heat exchanger. By utilizing this model, predictions can be made about how altering the independent variables of the system will change the outputs. There are many independent variables and considerations to account for in the model. If done so correctly, accurate predictions can be made about the system.
Types of Heat Exchangers
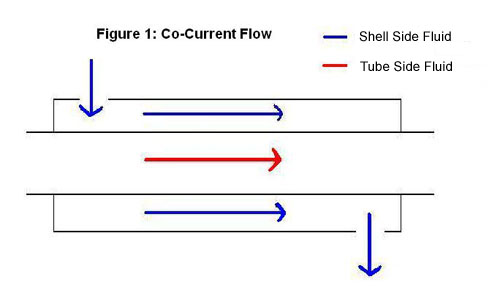
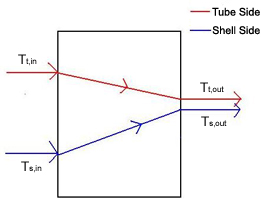
1. Double - Pipe Heat Exchanger
A double-pipe heat exchanger is the simplest type of heat exchanger and can operate with co-current (Figure 1) or counter-current (Figure 2) flow. The design consists of a single small pipe (tube-side) inside of a larger one (shell-side). A co-current heat exchanger is most commonly used when you want the exiting streams to leave the exchanger at the same temperature. A counter-current heat exchanger is used more often than co-current because they allow for a more efficient transfer of energy.


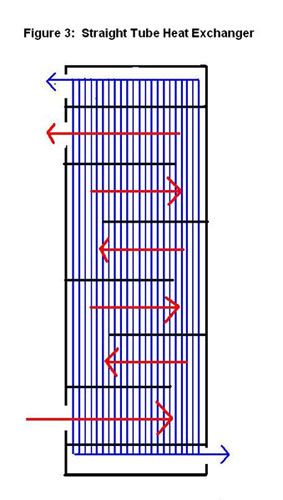
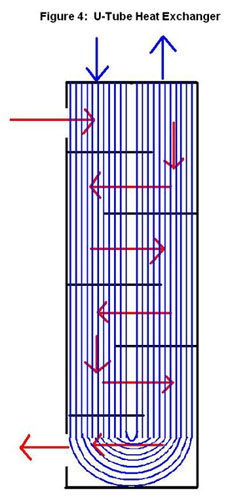
2. Shell-and-Tube Exchanger
A shell-and-tube exchanger is used for larger flows, which are very common in chemical process industries. The design of this exchanger is a shell with a bundle of tubes inside. The tubes are in parallel and a fluid flows around them in the shell. There are many different arrangements such as straight (Figure3) or u-tube (Figure 4). Each arrangement allows for a different type of flow such as co-current, counter-current and cross flow. The tube-side can have one or more passes to increase the energy exchange from the tube-side fluid. The shell-side may contain baffles, or walls, that channel the fluid flow and induce turbulence, and thus, increase energy exchange. Correlations can be developed to predict the increase in energy exchange. These correlations are out of the scope of this article.
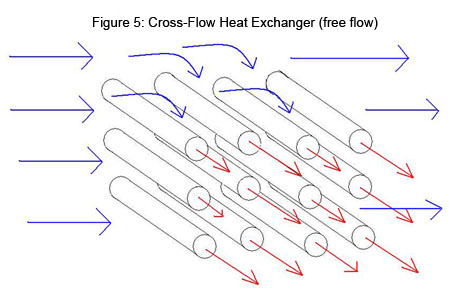
3. Cross-flow Exchanger
The most common application for a cross-flow heat exchanger is when a gas is being heated or cooled. This device consists of multiple tubes in parallel, usually containing a liquid, and the exterior gas flows across the tubes. In some cases the air is confined in separate flow chambers, such as fins, and in others it is open to flow freely (Figure 5).
Dynamic Modeling of Heat Exchangers
Since heat exchangers are so widely used in industry, it necessary for a chemical engineer to be able to optimize and control the system and know how independent variables will affect the outputs from teh system. To do this, a dynamic model is developed and utilized.
A dynamic model of a heat exchanger may be used, for example, to predict how a change in the fluid flowrates or the addition of an insulating jacket will affect the outlet temperature of the product stream. The model uses ordinary differential equations (ODEs) to describe the process and, using a program like Microsoft EXCEL, gives plots of the variables vs. time for the entire process. There are many independent variables in a heat exchanger, which can cause modeling to be very complex since multiple ODEs are required to define all of the process variables.
Some of the independent variables in a heat exchanger system include:
Shell-side:
- fluid
- flowrate
- temperature
- number of baffles
Tube-side:
- fluid
- flowrate
- temperature
- number of passes
Flow configuration
- Co-current
- Counter-current
- Cross flow
Insulating jacket
The primary dependent variable of concern is the outlet temperature of the product stream (usually the tube-side fluid.) The outlet temperature, in a controlled system, is monitored by a sensor. The sensor then transmits a signal to an actuating device of one or more of the independent variables (usually shell-side flow controller) to perform some desired response.
Modeling with ODEs
The following section outlines the method for developing a dynamic model of a heat exchanger. The model is for a double-pipe heat exchanger that has the ability to flow in co-current or counter-current configurations and the option of an external insulating jacket. It assumes constant fluid properties and perfect heat transfer through the metal of the tubing. The outlet temperature of the tube-side fluid is monitored by a temperature sensor, and the flow rate of the shell-side fluid is controlled by a actuated flow-controlling device.
Energy Balance
An energy balance is first performed on the tube-side fluid.
\[\text{Rate of accumulation of thermal energy in tube-side fluid} = \text{rate of energy in} - \text{Rate of energy out} - \text{Heat transferred from shell-side} \label{1} \]
The left-most term in the energy balance in Equation \ref{1} is the amount of thermal energy that accumulates in the tube-side fluid and causes a change in its outlet temperature. The terms on the right side of the above energy balance describe the thermal energy of the fluid flowing in and the fluid flowing out and the amount of heat transfer from the shell side fluid. In the term for heat transfer from the shell-side, the temperatures are the temperatures of the outlet streams. The outlet temperatures will change according to whether you are running co-currently or counter-currently. The energy balance is written as:
\[m c_{p, t} \frac{d T_{t, o u t}}{d t}=\rho c_{p, t} F_{t, i n} T_{t, i n}-\rho c_{p, t} F_{t, o u t} T_{t, o u t}-\frac{k A_{i}}{\Delta z}\left(T_{t, o u t}-T_{s, o u t}\right) \label{2} \]
where,
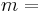 mass of the fluid =
mass of the fluid = 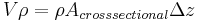
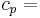 constant pressure heat capacity of the fluid
constant pressure heat capacity of the fluid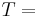 Temperature
Temperature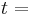 time
time conductive heat transfer coefficient
conductive heat transfer coefficient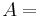 surface area of tube that fluid contacts
surface area of tube that fluid contacts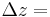 length of tube
length of tube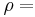 density of the fluid
density of the fluid volumetric flowrate of the fluid
volumetric flowrate of the fluid
and subscripts denote
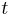 - tube-side fluid
- tube-side fluid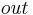 - outlet
- outlet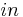 - inlet
- inlet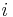 - inside
- inside
An similar energy balance is next performed on the shell-side fluid.
\[\text{Rate of accumulation of thermal energy in tube-side fluid} = \text{rate of energy in} - \text{Rate of energy out} - \text{Heat transferred to tube-side fluid} - \text{Rate of heat loss to the surroundings} \label{3} \]
The left-most term in the above energy balance is the amount of thermal energy that accumulates in the shell-side fluid and causes a change in its outlet temperature. The terms on the right side of the above energy balance describe the thermal energy of the fluid flowing in and the fluid flowing out, heat transfer to the tube-side fluid, and also the heat lost by convection to the surroundings. The energy is written as;
\[m c_{r, s} \frac{d T_{s, out}}{d t}-\rho c_{p, s} F_{s, sn} T_{s, i n}-\rho c_{p, s} F_{s, cut} T_{s, out}-\frac{k \cdot A_{o}}{\Delta z}\left(T_{s, cut}-T_{t, o u t}\right)-h . A_{s}\left(T_{s}-T_{\infty}\right) \label{4} \]
where,
 = coefficient of convective heat transfer for air
= coefficient of convective heat transfer for air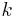 - conductive heat transfer coefficient.
- conductive heat transfer coefficient.
and subscripts denote
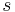 - shell-side fluid
- shell-side fluid - air
- air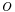 - outside of tube
- outside of tube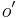 - outside of shell
- outside of shell
Considerations
There are considerations and simplifications you can make in order to solve the differential energy balances. The validity of these assumptions depends on how accurate of a model you require.
1. The heat capacity of the fluid may be temperature dependent. If this is the case, a polynomial equation could be written for the Cp values of each of the fluids. It would take the form-
\[C_{p}=a+b T+c T^{2}+d T^{3} \label{5} \]
Values of a, b, c, and d are properties of the fluid and can be found in Perry's Chemical Engineers' Handbook.
It should also be noted that if the fluids in the process are gases, their fluid properties will be affected by changes in pressure and the use of a constant Cp value would be inappropriate.
2. The density of the fluid may be temperature dependent. This would be likely if the fluid were a vapor, as in the case of using steam as the shell-side fluid to heat the tube-side process fluid. If this is the case, a differential equation could be written for the 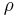 value of the fluid and would take the form-
value of the fluid and would take the form-
\[\frac{d \rho}{d T} \propto C \label{6} \]
where \(C\) is the coefficient of cubic expansion (relates kinetic energy to temperature).
3. Heat loss to the surroundings may be neglected. This would be the case if the heat exchanger is well insulated or if the shell-side fluid is about the same as ambient temperature. In this case-
\[h A\left(T_{s}-T_{\infty}\right)=0 \label{7} \]
4. The temperature sensor may have an inherent time delay. This means the temperature output from the sensor lags the actual temperature at the time of the reading. The temperature lag may be accounted for with the differential equation-
\[\frac{d T_{\text {outlet}, \text {sensor}}}{d t}=\frac{1}{\tau_{T s}}\left(T_{\text {outlet}, \text {actual}}-T_{\text {outlet}, \text {sensor}}\right) \label{8} \]
where  = time constant for the temperature sensor.
= time constant for the temperature sensor.  is a process parameter and usually ranges from 6 to 20 seconds depending on the properties of the sensor. This value would either be given in literature from the manufacturer or would have to be determined through experimentation.
is a process parameter and usually ranges from 6 to 20 seconds depending on the properties of the sensor. This value would either be given in literature from the manufacturer or would have to be determined through experimentation.
5. The actuator system for the control valve may have a slow dynamic response. When the actuator system is based on a control valve, the response to the pressure change is slower than the flow through the valve. The flow rate through a control valve can be modeled with the differential equation-
\[\frac{d Q_{\text {actual}}}{d t}=\frac{1}{\tau_{v}}\left(Q_{\text {setpoint}}-Q_{\text {actual}}\right) \label{9} \]
where 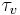 = time constant for the flow control valve.
= time constant for the flow control valve. 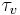 is a process parameter and usually ranges from 0.5 to 2 seconds depending on the properties of the sensor. This value would have to be determined through experimentation.
is a process parameter and usually ranges from 0.5 to 2 seconds depending on the properties of the sensor. This value would have to be determined through experimentation.
Using EXCEL to Solve ODEs
Since temperature of the heat exchanger varies across the metal as well as along the length of the pipe, a partial derivative for how temperature varies with length must be described. In order to solve this problem using excel, an approximation of length was used. Instead of taking the partial derivative across the length with respect to temperature, the pipe was divided into differential segments, Δz. Ideally Δz is an infinitesimally small cross section of the length of the heat exchanger. We will assume that through this differential segment, the temperature of the liquid that leaves the segment is the same as the temperature of the liquid within the segment. Since we are assuming the same temperature for the exiting streams as the inside of the segment, the choice of length for these Δz’s helps dictate the accuracy of the solution. The combination of these differential units allows us to model a heat exchanger without the use of partial derivatives. The figure below shows an example of the simplification where the heat exchanger is split into three segments (Figure 6).
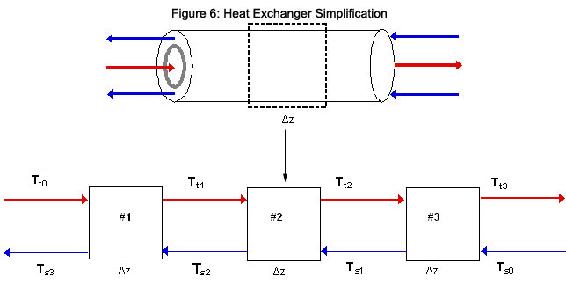
To begin modeling, start by solving the appropriate energy balance (either Equation \ref{2} or \ref{4}) for 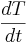 and make any simplifications necessary. Then use a method to solve ODEs in Excel, such as Euler's or Heun's. Go here: ExcelModelingODE for further explanation on how to set up an Excel spreadsheet using these methods. For each unit, Δz, and each fluid in that unit of the heat exhanger, you should have an approximation equation. Because ideally \(Δz\) represents an infinitesimal section, it follows from the first assumption that we can take the temperature in Δz as being the exit temperature of the hot and cold streams for the \(Δz\)’s respectively.
and make any simplifications necessary. Then use a method to solve ODEs in Excel, such as Euler's or Heun's. Go here: ExcelModelingODE for further explanation on how to set up an Excel spreadsheet using these methods. For each unit, Δz, and each fluid in that unit of the heat exhanger, you should have an approximation equation. Because ideally \(Δz\) represents an infinitesimal section, it follows from the first assumption that we can take the temperature in Δz as being the exit temperature of the hot and cold streams for the \(Δz\)’s respectively.
The equation for Euler's Method takes the form:
\[T_{h 1}\left(t_{i+h}\right)=T_{h 1}\left(t_{i}\right)+\Delta t\left[\frac{d T}{d t}\left(t_{i}\right)\right] \label{10} \]
The equation for Heun's Method takes the form:
\[T_{h_{1}}\left(t_{i+1 h}\right)=T_{h_{1}}\left(t_{i}\right)+\Delta\left[\frac{1}{2} \frac{d T}{d t}\left(t_{i} T_{i}\right)+\frac{1}{2} \frac{d T}{d t}\left(t_{i+h} T_{i+1 h_{i}}\right)\right] \label{11} \]
The temperatures can then be plotted versus time in order to model how the system inputs affect heat exchange. The following examples walk you through a model of a simple heat exchanger in Excel.
As a process engineer in a chemical processing company, you were assigned to scale up a process for your company’s latest and greatest chemical. Between one of the steps of the reaction, it is necessary to quickly and efficiently cool down the solution from 330 K before allowing it to enter the next step. From your previous knowledge, you know that a heat exchanger is necessary and the counter current heat exchanger is the most efficient to achieve a desired temperature. You decide to use cold water entering in at 250 K as your coolant since it is relatively inexpensive. In order to allow for the plant engineers in the future to have more control, create a model to determine when this process will go to steady state and graph the temperature profiles of the outlet streams. You can assume the heat exchanger is perfectly insulated and that there is perfect conduction through the metal from shell-side fluid to the tube-side fluid, and this conduction is described by the heat transfer coefficient, k, between the two fluids.
General Relevant Information:
- Tair=296.15 K (Temp. of the Air)
- ri=0.1 m (Inner Diameter of Inner Tube)
- ro=0.12 m (Outer Diameter of Inner Tube)
- ro'=0.15 m (Outer Diameter of Outer Tube)
- Δz=1 m (Increment of length)
- k=450000 W/m2*K (heat transfer coefficient between shell and tube-side fluids)
Shell Side Fluid Information (Cold Water)
- Cps=4185 J/kg*K (shell side fluid heat capacity)
- T0s=250 K (input temp. of shell side fluid)
- As=0.02543 m (cross sectional area where shell side fluid is present)
- ρs=1000 kg/m^3 (density of shell side fluid)
- Fs=0.1 m3/s (volumetric flow rate of shell side fluid)
Tube Side Fluid Information (Solution)
- Cpt=1200 J/kg*K (tube side fluid heat capacity)
- T0t=330 K (input temp. of tube side fluid)
- At=0.0314 m (cross sectional area where tube side fluid is present)
- ρt=1030 kg/m^3 (density of tube side fluid)
- Ft=0.2 m3/s (volumetric flow rate of tube side fluid)
Solution
The general Algorithm can be followed to develop the Excel model.
- 1. Make a spreadsheet that has all relevant process information (ie: T inputs, ρ values, etc).
- 2. Perform an overall energy balance for the tube-side and shell-side fluids. Make simplifications and state assumptions. Solve for
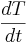
- 3. Divide the heat exchanger into smaller segments of length Δz
- 4. In your spreadsheet, set up a column for time. In the first row, start at t=0 and then increase time by Δh down the column.
- 5. Set up a column for the incoming tube-side temperature, Tt0. The value of incoming temperature is inputted by the user. Do the same for the shell-side temperature, Ts0.
- 6. Set up a column for the exiting tube-side temperature from each Δz unit. Do the same for the shell-side temperatures. For each of these temperature columns:
- a. In the first row, make an initial guess of the temperature. This is usually done by setting the temperature equal to the temperature of the stream coming into the heat exchanger.
- b. In subsequent rows, input the Euler’s equation (Eq 10) by referencing the appropriate cells for the process information and take all temperatures from time, ti, which are the temperatures in the row above.
- 7. Make a graph of variables of interest (Temperatures) vs. time.
The graph below illustrates how the exiting hot and cold temperature changes over a short period of time.

For a more detailed view of this process please see the attached spreadsheet:
Again, you are working on the same process, but your supervisor requires you to have a more accurate description of the dynamics of the system. Being as bright as you are, you decide to utilize the 2nd order Runga Kutta method, known as the Heun's method.
Solution
Follow the Algorithm in Example 1, except in step 6b, use the equation for Heun's method, Eq 11.
The graph below illustrates how the exiting hot and cold temperature changes over a short period of time.
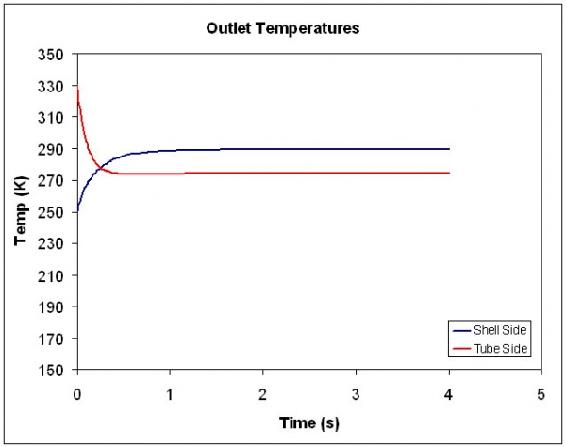
For a more detailed view of this process please see the attached spreadsheet:
A month after you developed a model of the heat exchanger used in the process for your company's latest and greatest chemical, one of the plant engineers calls you and says that at t=2s into the process, the temperature of the incoming fluid changes abruptly from 330K to 300K. How do the temperatures of the outlet streams react to this change. Use the information and model from Example 1.
Solution
The Excel spreadsheet can be modified so that at time t=2s, the incoming temperature of the tube-side fluid is 300K. The graph below illustrates how the exiting hot and cold temperature changes over a short period of time.
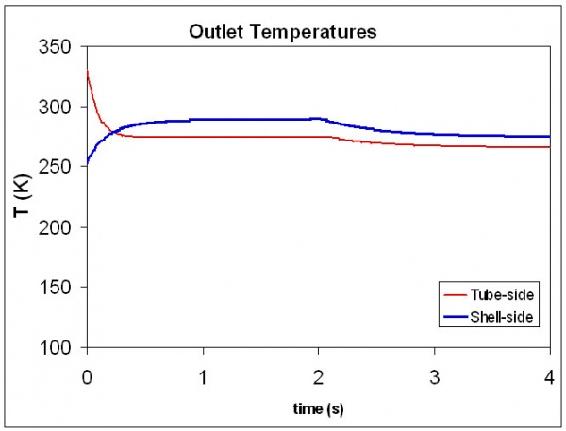
For a more detailed view of this process please see the attached spreadsheet:
Tube-side Temp Change
References
- Riggs, James B.; Karim, M. Nazmul. Chemical and Bio-Process Control, Texas Tech University, Ferret Publishing.
Contributors and Attributions
- Authors: Teresa Misiti, Carly Ehrenberger, Danesh Deonarain, Georgina Mang


