3.3.1: Actual Center of Mass
- Page ID
- 644
In many engineering problems, the knowledge of center of mass is required to make the calculations. This concept is derived from the fact that a body has a center of mass/gravity which interacts with other bodies and that this force acts on the center (equivalent force). It turns out that this concept is very useful in calculating rotations, moment of inertia, etc. The center of mass doesn't depend on the coordinate system and on the way it is calculated. The physical meaning of the center of mass is that if a straight line force acts on the body in away through the center of gravity, the body will not rotate. In other words, if a body will be held by one point it will be enough to hold the body in the direction of the center of mass. Note, if the body isn't be held through the center of mass, then a moment in additional to force is required (to prevent the body for rotating). It is convenient to use the Cartesian system to explain this concept. Suppose that the body has a distribution of the mass (density, \(\rho\)) as a function of the location. The density ``normally'' defined as mass per volume. Here, the the line density is referred to density mass per unit length in the \(x\) direction.
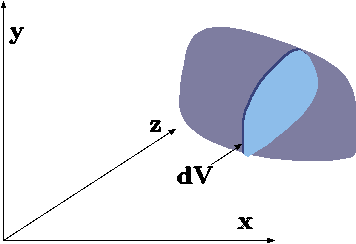
Fig. 3.2. Description of how the center of mass is calculated.
In \(x\) coordinate, the center will be defined as \[\bar{x} = \frac{1}{m}\int_V x\rho \left(x\right) dV \] Here, the \(dV\) element has finite dimensions in y–z plane and infinitesimal dimension in the \(x\) direction (see Figure 3.2). Also, the mass, \(m\) is the total mass of the object. It can be noticed that center of mass in the x–direction isn't affected by the distribution in the \(y\) nor by \(z\) directions. In same fashion the center of mass can be defined in the other directions as following
\(x_i\) of Center Mass
\[\bar{x_{i}} = \frac{1}{m}\int_V x_{i}\rho \left(x_{i}\right) dV \]
where \(x_{i}\) is the direction of either, \(x\), \(y\), or \(z\). The density, \(\rho\left(x_{i}\right)\) is the line density as a function of \(x_{i}\). Thus, even for solid and uniform density the line density is a function of the geometry.
Contributors and Attributions
Dr. Genick Bar-Meir. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or later or Potto license.


