3.4.2.1: General Discussion
- Page ID
- 649
For body with thickness, \(t\) and uniform density the following can be written \[I_{xxm} = \int_{m} r^{2} dm = \rho t \quad \int_{A} r^{2} dA \] The moment of inertia about axis is \(x\) can be defined as
Moment of Inertia
\[I_{xx} = \int_{A} r^{2} dA = \frac{I_{xxm}}{\rho t} \]
where \(r\) is distance of \(dA\) from the axis \(x\) and \(t\) is the thickness.
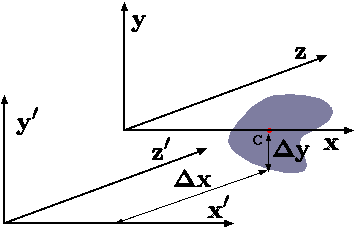
Fig. 3.4. The schematic that explains the summation of moment of inertia.
Any point distance can be calculated from axis \(x\) as \[x = \sqrt{y^{2} + z^{2}}\] Thus, equation 18 can be written as \[I_{xx} = \int_{A} \left(y^{2} + z^{2}\right)dA \] In the same fashion for other two coordinates as \[I_{yy} = \int_{A} \left(x^{2} + z^{2}\right)dA \] \[I_{zz} = \int_{A} \left(x^{2} + y^{2}\right)dA \]
Contributors and Attributions
Dr. Genick Bar-Meir. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or later or Potto license.


