4.3.2.1: Measuring the Atmospheric Pressure
- Page ID
- 663
One of the application of this concept is the idea of measuring the atmospheric pressure. Consider a situation described in Figure 4.3. The liquid is filling the tube and is brought into a steady state. The pressure above the liquid on the right side is the vapor pressure. Using liquid with a very low vapor pressure like mercury, will result in a device that can measure the pressure without additional information (the temperature).
Example 4.4
Calculate the atmospheric pressure at \(20^{\circ}C\). The high of the Mercury is 0.76 [m] and the gravity acceleration is 9.82[\(m/sec\)]. Assume that the mercury vapor pressure is 0.000179264[kPa]. The description of the height is given in Figure 4.3. The mercury density is 13545.85[\(kg/m^3\)].
Solution 4.4
The pressure is uniform or constant plane perpendicular to the gravity. Hence, knowing any point on this plane provides the pressure anywhere on the plane. The atmospheric pressure at point \(a\) is the same as the pressure on the right hand side of the tube. Equation (15) can be utilized and it can be noticed that pressure at point \(a\) is
\[
P_{a} = \rho \, g \, h + P_{vapor}
\label{static:eq:vaporP}
\]
\[
P_a = 13545.85 \times 9.82 \times 0.76
\sim 101095.39 [Pa] \sim 1.01[Bar]
\]
The vapor pressure is about \(1 \times 10^{-4}\) percent of the total results.
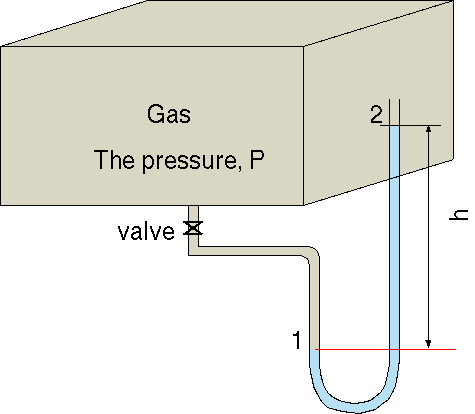
Fig. 4.6 Schematic of gas measurement utilizing the ``U'' tube.
The main reason the mercury is used because of its large density and the fact that it is in a liquid phase in most of the measurement range. The third reason is the low vapor (partial) pressure of the mercury. The partial pressure of mercury is in the range of the 0.000001793[Bar] which is insignificant compared to the total measurement as can be observed from the above example.
Example 4.5
A liquid \(a\) in amount \(H_a\) and a liquid \(b\) in amount \(H_b\) in to an U tube. The ratio of the liquid densities is \(\alpha = \rho_1/\rho_2\). The width of the U tube is \(L\). Locate the liquids surfaces.
Solution 4.5
The question is to find the equilibrium point where two liquids balance each other. If the width of the U tube is equal or larger than total length of the two liquids then the whole liquid will be in bottom part. For smaller width, \(L\), the ratio between two sides will be as
\[
\rho_1\,h_1 = \rho_2\,h_2 \rightarrow h_2 = \alpha \, h_1
\]
The mass conservation results in
\[
H_a + H_b = L + h_1 + h_2
\]
Thus two equations and two unknowns provide the solution which is
\[
h_1 = \dfrac{H_a + H_b - L}{1+\alpha}
\]
\[
h_1 \, \rho_b + h_2\, \rho_a = h_3\, \rho_a
\]
where \(h_1\) is the height of liquid \(\mathbf{b}\) where \(h_2\) is the height of "extra'' liquid \(\mathbf{a}\) and same side as liquid \(\mathbf{b}\) and where \(h_3\) is the height of liquid \(\mathbf{b}\) on the other side. When in this case \(h_1\) is equal to \(H_b\). The additional equation is the mass conservation as
\[
H_a = h_2+L+h_3
\]
The solution is
\[
h_2 = \dfrac{(H_a-L)\,\rho_a - H_b\rho_b}{2\,\rho_a}
\]
Contributors and Attributions
Dr. Genick Bar-Meir. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or later or Potto license.


