7.5: Examples of Integral Energy Conservation
- Page ID
- 736
Example 7.1
Consider a flow in a long straight pipe. Initially the flow is in a rest. At time, \(t_0\) the

Fig. 7.6 Flow in a long pipe when exposed to a jump in the pressure difference.
a constant pressure difference is applied on the pipe. Assume that flow is incompressible, and the resistance or energy loss is \(f\). Furthermore assume that this loss is a function of the velocity square. Develop equation to describe the exit velocity as a function of time. State your assumptions.
Solution 7.1
The mass balance on the liquid in the pipe results in
\[
\label{unsteadyPipe:massIni}
0 = \overbrace{\int_V \dfrac{\partial \rho}{\partial t} dV}^{=0} +
\overbrace{\int_A \rho\,U_{bn} dA}^{=0} + \int_A \rho\,U_{rn} dA
\Longrightarrow \cancel{\rho}\cancel{A}\,U_{in} = \cancel{\rho}\cancel{A}\,U_{exit}
\]
\[
\label{unsteadyPipe:energyIni1}
\begin{array}{rcl}
\dot{Q} - \overbrace{\dot{W}_{shear}}^{=0} + & \overbrace{\dot{W}_{shaft}}^{=0} =
\displaystyle \int_V \dfrac{d}{dt} \left( E_u + \dfrac{U^2}{2} + g\,z\right)\,\rho\, dV + \
& \displaystyle \int_S \left( h + \dfrac{U^2} {2} + g\,z \right) U_{rn}\, \rho \,dA +
\displaystyle \int_S P U_{bn} dA
\end{array}
\]
The boundaries shear work vanishes because the same arguments present before (the work, where velocity is zero, is zero. In the locations where the velocity does not vanished, such as in and out, the work is zero because shear stress are perpendicular to the velocity). There is no shaft work and this term vanishes as well. The first term on the right hand side (with a constant density) is
\[
\label{unsteadyPipe:fTerm}
\rho \int_{V_{pipe}} \dfrac{d}{dt} \left( E_u + \dfrac{U^2}{2}+
\overbrace{g\,z}^{\scriptsize constant} \right)\,dV =
\rho \,U\,\dfrac{d\,U}{dt} \overbrace{V_{pipe}}^{L\,\pi\,r^2}
+ \rho \, \int_{V_{pipe}} \dfrac{d}{dt} \left(E_u\right)\,dV
\]
where \(L\) is the pipe length, \(r\) is the pipe radius, \(U\) averaged velocity. In this analysis, it is assumed that the pipe is perpendicular to the gravity line and thus the gravity is constant. The gravity in the first term and all other terms, related to the pipe, vanish again because the value of z is constant. Also, as can be noticed from equation (112), the velocity is identical (in and out). Hence the second term becomes
\[
\label{unsteadyPipe:sTerm}
\int_A \left( h + \left(\cancelto{constant}{\dfrac{U^2}{2} + g\,z}\right) \right) \rho\,U_{rn} dA =
\int_A \overbrace{\left( E_u + \dfrac{P}{\rho} \right)}^{h} \,\rho\,U_{rn} dA
\]
Equation (115) can be further simplified (since the area and averaged velocity are constant, additionally notice that \(U = U_{rn}\)) as
\[
\label{unsteadyPipe:sTerms}
\int_A \left( E_u + \dfrac{P}{\rho} \right) \,\rho\,U_{rn} dA = {\Delta P\,U\, A} +
\int_A \rho\,E_u\,U_{rn}\, dA
\]
The third term vanishes because the boundaries velocities are zero and therefore
\[
\label{unsteadyPipe:tTerm}
\int_A P\,\,U_{bn} dA = 0
\]
Combining all the terms results in
\[
\label{unsteadyPipe:combinedEnergyIni}
\dot{Q} = \rho \,U\,\dfrac{d\,U}{dt} \overbrace{V_{pipe}}^{L\,\pi\,r^2}
+ \rho \,\dfrac{d}{dt} \int_{V_{pipe}} E_u\,dV +\Delta P\,U \,dA +
\int_A \rho\,E_u\,U\,dA
\]
equation (118) can be rearranged as
\[
\label{unsteadyPipe:combinedEnergy2}
\overbrace{\dot{Q} - \rho \,\int_{V_{pipe}} \dfrac{d \left(E_u \right)}{dt} \,dV
- \int_A \rho\,E_u\,U\,dA}^{-K\dfrac
Callstack:
at (Bookshelves/Civil_Engineering/Book:_Fluid_Mechanics_(Bar-Meir)/07:_Energy_Conservation/7.5:_Examples_of_Integral_Energy_Conservation), /content/body/div[2]/p[10]/span, line 1, column 2
= \rho \,{L\,\pi\,r^2}\, U\,\dfrac{d\, U }{dt}
+ \left( P_{in} - P_{out} \right)\,U
\] The terms on the LHS (left hand side) can be combined. It common to assume (to view) that these terms are representing the energy loss and are a strong function of velocity square . Thus, equation (119) can be written as
\[
\label{unsteadyPipe:combinedEnergy1}
- K\,\dfrac{U^2}{2} =
\rho \,{L\,\pi\,r^2}\,U\, \dfrac{d\,U}{dt}
+ \left( P_{in} - P_{out} \right) \,U
\]
Dividing equation (120) by \(K\,U/2\) transforms equation (??) to
\[
\label{unsteadyPipe:combinedEnergy}
{U} + \dfrac{2\,\rho \,{L\,\pi\,r^2}}{K} \dfrac{d\,U}{dt}
= \dfrac{2 \left( P_{in} - P_{out} \right) }{K}
\]
Equation (121) is a first order differential equation. The solution this equation is described in the appendix and which is
\[
\label{unsteadyPipe:sol1}
U=\text{ e}^{-\left(
\dfrac{t\,K}{2\,\pi \,{r}^{2}\,\rho\,L}\right)}\,
\left( \dfrac{2\,\left( P_{in} - P_{out} \right)
\mbox{\huge e}^{\left(\dfrac{t\,K}{2\,\pi \,{r}^{2}\,\rho\,L}\right)}}{K} + c
\right)
\,\text{ e}^{\left(\dfrac{2\,\pi \,{r}^{2}\,\rho\,t\,L}{K} \right)}
\]
Applying the initial condition, \(U(t=0) = 0\) results in
\[
\label{unsteadyPipe:solWini}
U=\dfrac{2\,\left( P_{in} - P_{out} \right)}{K}
\left( 1- \mbox{\huge e}^{- \left(\dfrac{t\,K}{2\,\pi \,{r}^{2}\,\rho\,L}\right)}\right)
\]
The solution is an exponentially approaching the steady state solution. In steady state the flow equation (121) reduced to a simple linear equation. The solution of the linear equation and the steady state solution of the differential equation are the same.
\[
\label{unsteadyPipe:ss}
U=\dfrac{2\,\left( P_{in} - P_{out} \right)}{K}
\]
Another note, in reality the resistance, K, is not constant but rather a strong function of velocity etc.). This function will be discussed in a greater extent later on. Additionally, it should be noted that if momentum balance was used a similar solution (but not the same) was obtained (why? hint the difference of the losses accounted for).
The following example combined the above discussion in the text with the above example (7.1).
Example 7.2
A large cylindrical tank with a diameter, \(D\), contains liquid to height, \(h\). A long pipe is connected to a tank from which the liquid is emptied. To analysis this situation,
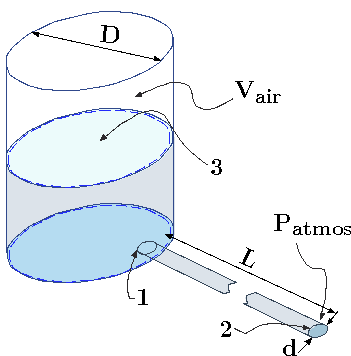
Fig. 7.7 Liquid exiting a large tank trough a long tube.
consider that the tank has a constant pressure above liquid (actually a better assumption of air with a constant mass.). The pipe is exposed to the surroundings and thus the pressure is \(P_{atmos}\) at the pipe exit. Derive approximated equations that related the height in the large tank and the exit velocity at the pipe to pressure difference. Assume that the liquid is incompressible. Assume that the resistance or the friction in the pipe is a strong function to the velocity square in the tank. State all the assumptions that were made during the derivations.
Solution 7.2

Fig. 7.8 Tank control volume for Example.
This problem can split into two control volumes; one of the liquid in the tank and one of the liquid in pipe. Analysis of control volume in the tank was provided previously and thus needed to be sewed to Example 7.1. Note, the energy loss is considered (as opposed to the discussion in the text). The control volume in tank is depicted in Figure 7.7.
Tank Control Volume
The effect of the energy change in air side was neglected. The effect is negligible in most cases because air mass is small with exception the "spring'' effect (expansion/compression effects). The mass conservation reads
\[
\label{longPipeTank:massIni}
\overbrace{\int_V \dfrac{\partial \rho}{\partial t} dV}^{=0} +
\int_A \rho\,U_{bn} dA + \int_A \rho\,U_{rn} dA = 0
\]
\[
\label{longPipeTank:massRTi}
\cancel{\rho}\,U_{1}\,A_{pipe} = \cancel{\rho} \,U_3\,\overbrace{\pi\,R^2}^{A_{tank}}
= \cancel{\rho} \,\dfrac{dh}{dt}\,\overbrace{\pi\,R^2}^{A_{tank}}
\]
It can be noticed that \(U_3 = dh/dt\) and \(D=2\,R\) and \(d=2\,r\) when the lower case refers to the pipe and the upper case referred to the tank. Equation (126) simply can be written when the area ratio is used (to be changed later if needed) as
\[
\label{longPipeTank:massRT}
U_{1}\,A_{pipe} = \dfrac{dh}{dt}\,{A_{tank}}
\Longrightarrow U_1 = \left( \dfrac{R}{r} \right)^2 \dfrac{dh}{dt}
\]
The boundaries shear work and the shaft work are assumed to be vanished in the tank. Therefore, the energy conservation in the tank reduces to
\[
\label{unsteadyPipe:energyIni}
\dot{Q} - \overbrace{\dot{W}_{shear}}^{=0} + \overbrace{\dot{W}_{shaft}}^{=0} =
\dfrac{d}{dt} \displaystyle \int_{V_t} \left( E_u + \dfrac
Callstack:
at (Bookshelves/Civil_Engineering/Book:_Fluid_Mechanics_(Bar-Meir)/07:_Energy_Conservation/7.5:_Examples_of_Integral_Energy_Conservation), /content/body/div[4]/div[1]/p[5]/span[1], line 1, column 4
\displaystyle \int_{A_3} P \overbrace{U_{bn}}^{U_3} dA
= \overbrace{\dfrac{d}{dt} \displaystyle \int_{V_t} E_u \rho\, dV + \int_{A_1} E_u\,\rho\,U_{rn}\,dA- \dot{Q}}^
{K\,\dfrac
Callstack:
at (Bookshelves/Civil_Engineering/Book:_Fluid_Mechanics_(Bar-Meir)/07:_Energy_Conservation/7.5:_Examples_of_Integral_Energy_Conservation), /content/body/div[4]/div[1]/p[5]/span[2], line 1, column 4
\] Similar arguments to those that were used in the previous discussion are applicable to this case. Using equation (38), the first term changes to
\[
\label{longPipeTank:unstadyT}
\begin{array}{rl}
\dfrac{d}{dt} \displaystyle \int_V \rho\,\left( \dfrac{U^2}{2} + g\,z\right) \, dV & \cong
\rho\, \dfrac{d}{dt} \left( \left[ \dfrac
Callstack:
at (Bookshelves/Civil_Engineering/Book:_Fluid_Mechanics_(Bar-Meir)/07:_Energy_Conservation/7.5:_Examples_of_Integral_Energy_Conservation), /content/body/div[4]/div[1]/p[6]/span, line 1, column 1
\] It is assumed that the exit velocity can be averaged (neglecting the velocity distribution effects). The second term can be recognized as similar to those by equation (45). Hence, the second term is
\[
\label{longPipeTank:secondOtherP}
\int_A \left( \dfrac{U^2}{2\dfrac{}{}} + \overbrace{g\,z}^{z=0}\right)\, U_{rn}\, \rho \,dA \cong
\dfrac{1}{2} \left( \dfrac{dh}{dt\dfrac{}{}} \dfrac{A_3}{A_1}\right)^2\, U_1 \, \rho \,A_1 =
\dfrac{1}{2} \left( \dfrac{dh}{dt\dfrac{}{}} \dfrac{R}{r}\right)^2\, U_1 \, \rho \,A_1
\]
The last term on the left hand side is
\[
\label{longPipeTank:lTerm}
\int_A P U_{bn} dA = P_{3}\,A\, \dfrac{dh}{dt}
\]
The combination of all the terms for the tank results in
\[
\label{longPipeTank:TenergyF}
\dfrac{d}{dt} \left( \left[ \dfrac
Callstack:
at (Bookshelves/Civil_Engineering/Book:_Fluid_Mechanics_(Bar-Meir)/07:_Energy_Conservation/7.5:_Examples_of_Integral_Energy_Conservation), /content/body/div[4]/div[1]/p[9]/span, line 1, column 1
+ \,\dfrac{K_t}{2\,\rho} \left( \dfrac{dh}{dt\dfrac{}{}}\right)^2 =
\dfrac{\left( P_3 - P_1 \right) } {\rho}
\]
Pipe Control Volume
The analysis of the liquid in the pipe is similar to Example 7.1. The conservation of the liquid in the pipe is the same as in Example 7.1 and thus equation (112) is used
\[
\label{longPipeTank:massPini}
U_{1} = U_{2}
\]
\[
\label{longPipeTank:combinedEnergy2}
{U_p} + \dfrac{4\,\rho \,{L\,\pi\,r^2}}{K_p} \dfrac{d\,U_p}{dt}
= \dfrac{2 \left( P_1- P_2 \right) }{K_p}
\]
where \(K_p\) is the resistance in the pipe and \(U_p\) is the (averaged) velocity in the pipe. Using equation (127) eliminates the \(U_p\) as
\[
\label{longPipeTank:combinedEnergy1}
\dfrac{dh}{dt} + \dfrac{4\,\rho \,{L\,\pi\,r^2}}{K} \dfrac{d^2\,h}{dt^2}
= \left(\dfrac{R}{r} \right)^2 \dfrac{2 \left( P_1 - P_2 \right) }{K_{p}}
\]
Equation (137) can be rearranged as
\[
\label{longPipeTank:combinedEnergy}
\dfrac{K_p}{2\,\rho} \left(\dfrac{r}{ R\dfrac{}{}} \right)^2
\left( \dfrac{dh}{dt\dfrac{}{}} + \dfrac{4\,\rho \,{L\,\pi\,r^2}}{K} \dfrac{d^2\,h}{dt^2} \right)
= \dfrac{ \left( P_1 - P_2 \right) }{\rho}
\]
Solution
The equations (138) and (134) provide the frame in which the liquid velocity in tank and pipe have to be solved. In fact, it can be noticed that the liquid velocity in the tank is related to the height and the liquid velocity in the pipe. Thus, there is only one equation with one unknown. The relationship between the height was obtained by substituting equation (127) in equation (138). The equations (138) and (134) have two unknowns (\(dh/dt\) and \(P_1\)) which are sufficient to solve the problem. It can be noticed that two initial conditions are required to solve the problem. } The governing equation obtained by from adding equation (138) and (134) as
\[
\label{longPipeTank:govEq}
\dfrac{d}{dt} \left(
\left[ \dfrac
Callstack:
at (Bookshelves/Civil_Engineering/Book:_Fluid_Mechanics_(Bar-Meir)/07:_Energy_Conservation/7.5:_Examples_of_Integral_Energy_Conservation), /content/body/div[4]/div[3]/p[2]/span, line 1, column 1
\overbrace{h\, A}^{V} \right)
- \dfrac{1}{2}\left( \dfrac{dh}{dt\dfrac{}{}} \right)^2 \left( \dfrac{A_3}{A_1\dfrac{}{}}\right)^2 \, U_1 \, \,A_1
+ \dfrac{K_t}{2\,\rho\dfrac{}{}} \left( \dfrac{dh}{dt\dfrac{}{}}\right)^2 \\ +
\dfrac{K_p}{2\,\rho} \left(\dfrac{r}{R\dfrac{}{}} \right)^2
\left( \dfrac{dh}{dt\dfrac{}{}} + \dfrac{4\,\rho \,{L\,\pi\,r^2}}{K} \dfrac{d^2\,h}{dt^2} \right)
= \dfrac{ \left( P_3 - P_2 \right) }{\rho}
\] The initial conditions are that zero initial velocity in the tank and pipe. Additionally, the height of liquid is at prescript point as
\[
\label{longPipeTank:iniCon}
\begin{array}{cc}
h(0) = & h_0 \
\dfrac{dh}{dt} (0) = & 0
\end{array}
\]
The solution of equation can be obtained using several different numerical techniques. The dimensional analysis method can be used to obtain solution various situations which will be presented later on.
Contributors and Attributions
Dr. Genick Bar-Meir. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or later or Potto license.


