3. Indirect Semiconductors
- Page ID
- 5960
Indirect-band-gap semiconductors, which follow the latter conditions discussed in the previous section, are defined by the fact that the minimum energy in the conduction band and the maximum energy in the valence band occur at different values of the crystal momentum. This means that a direct transition from the valence to the conduction band of an electron requires a photon of energy higher than that of the band gap, because the curves are parabolic. However, is it possible to make the transition at lower energies, but we require a new type of particle: the phonon.
The phonon is a quantum mechanical manifestation of thermal vibrations in the crystal lattice, or the vibrations of the atoms that jiggle within the lattice. The difference between phonons and photons is most notably that photons have relatively large energy and low momentum, whereas phonons have low energy but large momentum1. It turns out that phonon exchange can bridge the indirect band gap; in a two-step process, consisting of a photon interaction and a phonon interaction, the electron can still be excited at relatively low energies to the conduction band (see Fig. 1). The following equation gives the minimum photon energy required to excite an electron to the conduction band:
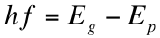
where Ep is the energy of an absorbed phonon with the required momentum to bridge the offset between the conduction band minimum and valence band maximum. This equation means that the energy of the photon must be equal to the difference between the energy required to cross the band gap and the energy due to the phonon’s momentum.
This two-step process, however, results in a much lower probability of absorption than in direct semiconductors, due to the fact that the process involves multiple particle interactions2. This means that light can pass a reasonable distance into the semiconductor before being absorbed. We can use the energy relation given above, with some theoretical deliberations, to give an absorption coefficient for transitions in an indirect semiconductor involving both phonon emission and absorption:
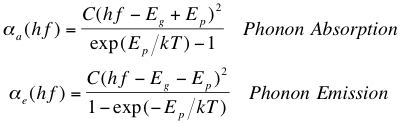
where C is a constant as given in the previous “section”, hf is the energy of the photon, k is the Boltzmann constant (1.38 x 10-23 Joules per Kelvin), and T is temperature. From this equation, we see that as temperature or energy of the photon increases while leaving all else fixed, the absorption coefficient increases (greatly for photon energy). Because both phonon emission and absorption are both possible for hf > Eg + Ep, the total absorption coefficient2 is then
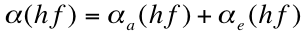
Keep in mind that the absorption coefficient depends on various parameters, differing from material to material and across a range of photon energies. We see that the case of indirect semiconductors is somewhat more complicated and problematic than for direct semiconductors, as the efficiency of absorption processes is limited by the lower probability of such ideal phonon exchanges. Silicon, a very prominent solar cell material, is actually an indirect semiconductor.
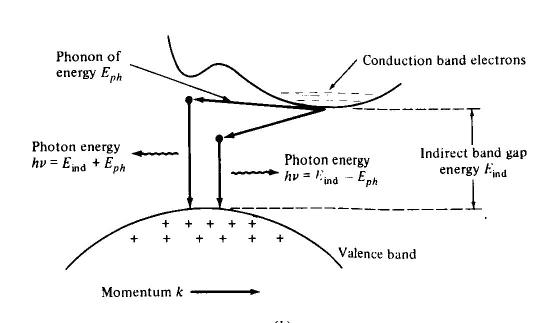
Fig. 1: Above is an example of phonon emission, where the phonons have an initial thermal energy that is translated to photons that cross the band gap directly. It is very important to note that no particle actually contains both the energy and momentum required to follow one of the paths illustrated; these paths represent virtual processes involving both phonons and photons. Also notice that the sign of the photon energy changes when the phonon has energy above or below the edge of the conduction band.
Source: <http://www.electronicspoint.com/indi...t-t226137.html>
References
1. Goetzberger, Adolf et.al. Crystalline Silicon Solar Cells. Chichester: John Wiley & Sons Ltd., 1998.
2. Green, Martin A. Solar Cells: Operating Principles, Technology, and System Applications. Englewood Cliffs: Prentice-Hall, Inc., 1982.Full book ordering information at www.pv.unsw.edu.au.

