13.3: The Equilibrium of Moments

The first additional condition is the equilibrium of moments of the wedge. Since the wedge is not subject to rotational accelerations in a stationary cutting process, the sum of the moments around any point on the wedge has to be zero. Here the tip of the blade is chosen for this point. First the equilibrium of moments is solved in order to find a relation between N₃ and N₄.

Figure 13-5: The equilibrium of moments on the wedge when cutting clay.

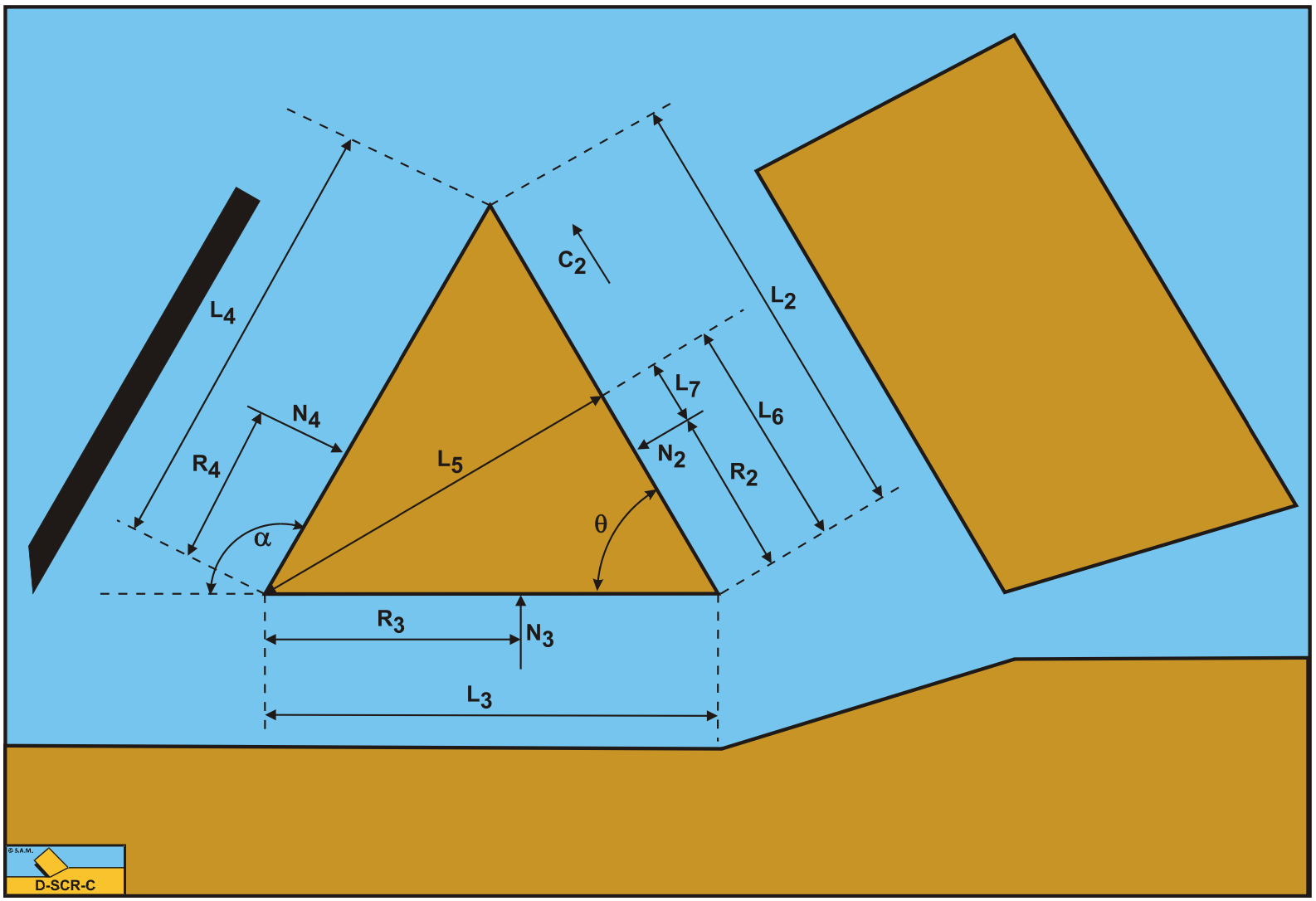
To solve the equilibrium of moments the lengths of the sides of the wedge and arms of the forces have to be determined.

The length of the shear plane A-B is:

\[\ \mathrm{L}_{1}=\frac{\mathrm{h}_{\mathrm{i}}}{\sin (\beta)}\tag{13-16}\]

The length of the front of the wedge A-C is:

\[\ \mathrm{L}_{2}=\frac{\mathrm{h}_{\mathrm{b}}}{\sin (\theta)}\tag{13-17}\]

The length of the bottom of the wedge A-D is:

\[\ \mathrm{L}_{3}=\mathrm{h}_{\mathrm{b}} \cdot\left(\frac{\mathrm{1}}{\tan (\theta)}-\frac{\mathrm{1}}{\tan (\alpha)}\right)\tag{13-18}\]

The length of the blade C-D is:

\[\ \mathrm{L}_{4}=\frac{\mathrm{h}_{\mathrm{b}}}{\sin (\alpha)}\tag{13-19}\]

The distance of the tip of the blade perpendicular to the front of the wedge is:

\[\ \mathrm{L}_{5}=\mathrm{L}_{3} \cdot \sin (\theta)\tag{13-20}\]

The distance from point A to the intersection point of the line going from the tip of the blade perpendicular to the front of the blade is.

\[\ \mathrm{L}_{6}=\mathrm{L}_{3} \cdot \cos (\theta)\tag{13-21}\]

The distance of the acting point of the force N₂ to the intersection point of the line going from the tip of the blade perpendicular to the front of the blade is:

\[\ \mathrm{L}_{7}=\mathrm{L}_{6}-\mathrm{R}_{2}\tag{13-22}\]

R₂ follows from the equilibrium of moments on the layer cut, assuming the forces on the shear plane act at half the length of the shear plane.

\[\ \mathrm{N}_{1} \cdot \mathrm{R}_{1}=\mathrm{N}_{2} \cdot \mathrm{R}_{2}\tag{13-23}\]

Now the equilibrium equation of moments can be derived according to:

\[\ \sum \mathrm{M}=\frac{\mathrm{N}_{4} \cdot \mathrm{L}_{4}}{2}-\frac{\mathrm{N}_{3} \cdot \mathrm{L}_{3}}{2}+\mathrm{N}_{2} \cdot \mathrm{L}_{7}-\mathrm{C}_{2} \cdot \mathrm{L}_{5}=\mathrm{0}\tag{13-24}\]

Both equation (13-11) and equation (13-24) don not contain the mobilized adhesive force A_m, giving the possibility to solve the two unknowns N₃ and N₄. To solve the normal force N3 first an expression for the normal force N₄ has to be derived based on the equilibrium of moments.

\[\ \mathrm{N}_{4}=\frac{\mathrm{2} \cdot\left(\mathrm{N}_{\mathrm{3}} \cdot \mathrm{L}_{\mathrm{3}} / \mathrm{2}-\mathrm{N}_{\mathrm{2}} \cdot \mathrm{L}_{\mathrm{7}}+\mathrm{C}_{\mathrm{2}} \cdot \mathrm{L}_{\mathrm{5}}\right)}{\mathrm{L}_{\mathrm{4}}}\tag{13-25}\]

Equation (13-11) and equation (13-25) should give the same result for the normal force N₄, thus:

\[\ \begin{array}{left}\frac{2 \cdot\left(\mathrm{N}_{3} \cdot \mathrm{L}_{3} / 2-\mathrm{N}_{2} \cdot \mathrm{L}_{7}+\mathrm{C}_{2} \cdot \mathrm{L}_{5}\right)}{\mathrm{L}_{4}}=\\
\mathrm{C}_{2} \cdot \sin (\alpha+\theta)-\mathrm{N}_{2} \cdot \cos (\alpha+\theta)+\mathrm{C}_{3} \cdot \sin (\alpha)+\mathrm{N}_{3} \cdot \cos (\alpha)\end{array}\tag{13-26}\]

This can be written as:

\[\ \begin{array}{left} \mathrm{N}_{3} \cdot\left(\frac{\mathrm{L}_{3}}{\mathrm{L}_{4}}-\cos (\alpha)\right) &=\mathrm{N}_{2} \cdot\left(\frac{\mathrm{L}_{7}}{2 \cdot \mathrm{L}_{4}}-\cos (\alpha+\theta)\right) \\ &+\mathrm{C}_{2} \cdot\left(-\frac{\mathrm{L}_{5}}{\mathrm{2} \cdot \mathrm{L}_{4}}+\sin (\alpha+\theta)\right)+\mathrm{C}_{3} \cdot \sin (\alpha) \end{array}\tag{13-27}\]

Now N₃ can be expressed in a number of known variables according to:

\[\ \begin{array}{left}\mathrm{N}_{3}&=\frac{\mathrm{N}_{2} \cdot\left(\frac{\mathrm{L}_{7}}{\mathrm{2} \cdot \mathrm{L}_{4}}-\cos (\alpha+\theta)\right)+\mathrm{C}_{2} \cdot\left(-\frac{\mathrm{L}_{5}}{2 \cdot \mathrm{L}_{4}}+\sin (\alpha+\theta)\right)}{\left(\frac{\mathrm{L}_{3}}{\mathrm{L}_{4}}-\cos (\alpha)\right)}\\ &+\frac{\mathrm{+C_3\cdot\sin(\alpha)}}{\mathrm{\left(\frac{L_3}{L_4}-cos(\alpha) \right)}}\end{array}\tag{13-28}\]

Substituting equation (13-28) in equation (13-11) gives a solution for the normal force N₄.

\[\ \mathrm{N}_{4}=\mathrm{C}_{2} \cdot \sin (\alpha+\theta)-\mathrm{N}_{2} \cdot \cos (\alpha+\theta)+\mathrm{C}_{3} \cdot \sin (\alpha)+\mathrm{N}_{3} \cdot \cos (\alpha)\tag{13-29}\]

Substituting equation (13-28) in equation (13-14) gives a solution for the mobilized adhesion A_m.

\[\ \mathrm{A}_{\mathrm{m}}=\mathrm{C}_{2} \cdot \cos (\alpha+\theta)+\mathrm{N}_{2} \cdot \sin (\alpha+\theta)+\mathrm{C}_{3} \cdot \cos (\alpha)-\mathrm{N}_{3} \cdot \sin (\alpha)\tag{13-30}\]

This results in a horizontal force of:

\[\ \mathrm{F}_{\mathrm{h}}=\mathrm{N}_{\mathrm{4}} \cdot \sin (\alpha)+\mathrm{A}_{\mathrm{m}} \cdot \cos (\alpha)\tag{13-31}\]

And in a vertical force of:

\[\ \mathrm{F}_{\mathrm{v}}=\mathrm{N}_{4} \cdot \cos (\alpha)-\mathrm{A}_{\mathrm{m}} \cdot \sin (\alpha)\tag{13-32}\]

Based on the experience with sand cutting it is assumed that the wedge angle θ can be determined by assuming that the horizontal force should be at a minimum for the angle chosen. It is very well possible that the mobilized adhesion is negative for large blade angles.