5.3: Rotation and strain- the relative motion of two nearby particles
- Page ID
- 18065
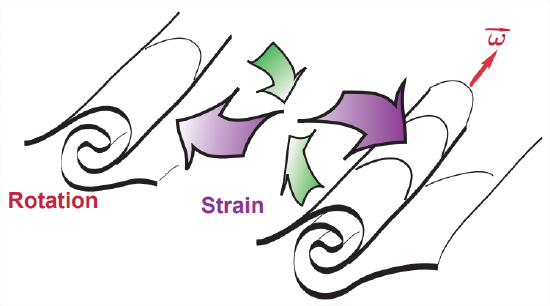

The complexity of flow can be halved, in a sense, by thinking of it as a combination of two simpler kinds of motion: rotation and strain (Figure \(\PageIndex{1}\)), with one or the other dominating at each point. We can then learn something useful by considering idealized flows consisting of rotation alone or strain alone.

Consider the instantaneous relative motion of two nearby fluid particles separated by the vector \(\Delta \vec{x}\) (Figure \(\PageIndex{2}\)). Their velocities are
\[\frac{D}{D t} \vec{x}=\vec{u}, \quad \text { and } \quad \frac{D}{D t}(\vec{x}+\Delta \vec{x})=\vec{u}+\Delta \vec{u}, \nonumber \]
and we can then subtract to see that
\[\frac{D}{D t} \Delta \vec{x}=\Delta \vec{u}.\label{eqn:1} \]
The ith component of the velocity difference \(\Delta\vec{u}\) can be written as
\[\Delta u_{i}=\frac{\partial u_{i}}{\partial x_{j}} \Delta x_{j}.\label{eqn:2} \]
The velocity gradient tensor \(\partial u_i/\partial x_j\) can be decomposed into symmetric and antisymmetric parts:
\[\frac{\partial u_{i}}{\partial x_{j}}=\frac{1}{2}\left(\frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}}\right)+\frac{1}{2}\left(\frac{\partial u_{i}}{\partial x_{j}}-\frac{\partial u_{j}}{\partial x_{i}}\right), \nonumber \]
or
\[\frac{\partial u_{i}}{\partial x_{j}}=e_{i j}+\frac{1}{2} r_{i j},\label{eqn:3} \]
where the symmetric part
\[e_{i j}=\frac{1}{2}\left(\frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}}\right)\label{eqn:4} \]
is called the strain rate tensor1 and the antisymmetric part (times two) is called the rotation tensor2:
\[r_{i j}=\frac{\partial u_{i}}{\partial x_{j}}-\frac{\partial u_{j}}{\partial x_{i}}\label{eqn:5} \]
Substituting in Equation \(\ref{eqn:2}\), we now write the velocity differential as
\[\Delta u_{i}=\frac{\partial u_{i}}{\partial x_{j}} \Delta x_{j}=e_{i j} \Delta x_{j}+\frac{1}{2} r_{i j} \Delta x_{j}\label{eqn:6} \]
Any region of a flow can be characterized as strain-dominated or rotation-dominated depending on the relative magnitudes of the two terms on the right-hand side of Equation \(\ref{eqn:3}\). More specifically, we can multiply Equation \(\ref{eqn:3}\) by itself and get
\[\left(\frac{\partial u_{i}}{\partial x_{j}}\right)^{2}=\left(e_{i j}+\frac{1}{2} r_{i j}\right)^{2}=e_{i j} e_{i j}+\frac{1}{4} r_{i j} r_{i j}\label{eqn:7} \]
The cross term \(e_{ij}r_{ij}\) is the product of a symmetric and an antisymmetric matrix and therefore vanishes identically (exercise 12). The remaining two terms are positive definite measures of the degree of strain and the degree of rotation. Vortices, not surprisingly, are rotation-dominated, e.g., the pair of corotating vortices shown in Figure \(\PageIndex{3}\). (The stream function for this vortex pair is shown in figure 5.2.1.) The rotation term is greatest in the two vortex cores located at \(x = \pm 1\) (Figure \(\PageIndex{3}\)a), while strain dominates in the region around the vortices, and especially between them (Figure \(\PageIndex{3}\)b, near \(x = 0\)).

The example in Figure \(\PageIndex{3}\) is highly simplified; in a real flow the strained and rotating regions are intertwined in very complex ways, but are still recognizable. Figure \(\PageIndex{4}\) shows the evolution of turbulence in a shear layer. It begins (Figure \(\PageIndex{4}\)a) with the growth of co-rotating vortices (cf. Figure \(\PageIndex{1}\)). These become unstable (Figure \(\PageIndex{4}\)b) and break down into turbulence (Figure \(\PageIndex{4}\)c). The turbulence eventually decays, leaving a stable shear layer thickened by turbulent mixing. In the phase of vigorous turbulence, the strain magnitude \(e^2_{ij}\) displays an intricate structure (Figure \(\PageIndex{5}\)). In the next two sections, we look more closely at the properties of rotation- and strain-dominated regions.

5.3.1 Rotation
The rotation tensor is closely related to a more familiar object: the vorticity vector \(\vec{\omega}\):
\[\underset{\sim}{r}=\left[\begin{array}{ccc}
0 & \frac{\partial u}{\partial y}-\frac{\partial v}{\partial x} & \frac{\partial u}{\partial z}-\frac{\partial w}{\partial x} \\
\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y} & 0 & \frac{\partial v}{\partial z}-\frac{\partial w}{\partial y} \\
\frac{\partial w}{\partial x}-\frac{\partial u}{\partial z} & \frac{\partial w}{\partial y}-\frac{\partial v}{\partial z} & 0
\end{array}\right]=\left[\begin{array}{ccc}
0 & -\omega_{3} & \omega_{2} \\
\omega_{3} & 0 & -\omega_{1} \\
-\omega_{2} & \omega_{1} & 0
\end{array}\right]\label{eqn:8} \]
Reverting to index notation, we may write this relationship in a much more compact form:
\[r_{i j}=-\varepsilon_{i j k} \omega_{k}\label{eqn:9} \]
The contribution of rotation to the velocity differential in Equation \(\ref{eqn:6}\) is now
\[\frac{1}{2} r_{i j} \Delta x_{j}=-\frac{1}{2} \varepsilon_{i j k} \omega_{k} \Delta x_{j}=\frac{1}{2}(\vec{\omega} \times \Delta \vec{x})_{i}\label{eqn:10} \]
Thus, the change in velocity due to rotation is perpendicular to both the separation vector and the local vorticity. A consequence of this is that rotation does not change the distance \(|\Delta \vec{x}|\) between the two particles; only strain can accomplish that. To show this explicitly, we write the equation for \(|\Delta \vec{x}|\) (or, equivalently, \(|\Delta \vec{x}|^2/2\)) in vector form:
\[\frac{D}{D t} \frac{1}{2}|\Delta \vec{x}|^{2}=\Delta \vec{x} \cdot \frac{D}{D t} \Delta \vec{x}=\Delta \vec{x} \cdot \Delta \vec{u}=\Delta \vec{x} \cdot\left(\underset{\sim}{e} \Delta \vec{x}+\frac{1}{2} \vec{\omega} \times \Delta \vec{x}\right)=\Delta \vec{x} \cdot \underset{\sim}{e} \Delta \vec{x} \nonumber \]
The second step above makes use of Equation \(\ref{eqn:1}\). Thus, changes in the distance between particles are cause only by strain.
5.3.2 Axisymmetric vortex models


Vortex motion is often approximately axisymmetric, i.e., invariant with respect to rotation about the vortex axis. Here we examine some very simple, axisymmetric vortex models. These are also called cylindrical, or circular, vortices.
Until now, we have measured space using Cartesian coordinates, but in some situations, curvilinear coordinates simplify the math. All of the mathematical constructs derived up to now can be expressed in curvilinear coordinates, and these expressions are listed in appendix I. The study of axisymmetric vortices is simplified using cylindrical polar coordinates (Figure \(\PageIndex{6}\)). In this case, every position in space has coordinates \({r,\theta,z}\) corresponding to the radial, azimuthal and axial directions, respectively. The corresponding velocity components are \({u_r,u_\theta ,u_z}\). The vorticity is then given as the curl of the velocity vector:
\[\vec{\nabla} \times \vec{u}=\left\{\frac{1}{r} \frac{\partial u_{z}}{\partial \theta}-\frac{\partial u_{\theta}}{\partial z}, \frac{\partial u_{r}}{\partial z}-\frac{\partial u_{z}}{\partial r}, \frac{1}{r} \frac{\partial\left(r u_{\theta}\right)}{\partial r}-\frac{1}{r} \frac{\partial u_{r}}{\partial \theta}\right\}. \nonumber \]
In an axisymmetric vortex, the vorticity is purely axial and depends only on the radial coordinate:
\[\vec{\omega}=\omega(r) \hat{e}^{(z)} ; \quad \omega(r)=\frac{1}{r} \frac{\partial\left(r u_{\theta}\right)}{\partial r}.\label{eqn:11} \]
The circulation around such a vortex at any radius \(r\) is just \(\Gamma(r) = 2\pi ru_\theta\) (show this). We’ll look at three kinds of vortex motion in this geometrical context.
Rigid rotation
In this case the vorticity is uniform. Solving Equation \(\ref{eqn:11}\) gives
\[u_{\theta}=\frac{\omega}{2} r. \nonumber \]
Note that the velocity is unbounded.
An irrotational vortex
In this case the motion is circular but the vorticity is zero. Solving Equation \(\ref{eqn:11}\) gives
\[u_{\theta}=\frac{C}{r}, \nonumber \]
where \(C\) is a constant of integration. The circulation is constant: \(\Gamma = 2\pi C\). This gives us a meaningful way to identify the constant:
\[u_{\theta}=\frac{\Gamma}{2 \pi r}. \nonumber \]
This velocity distribution is unbounded at the origin.
To understand how motion can be circular but irrotational, consider the hand motions illustrated in Figure \(\PageIndex{7}\). When you wave to someone (Figure \(\PageIndex{7}\)a), the orientation of your hand changes. When you wipe a window (Figure \(\PageIndex{7}\)b), your hand moves in a circle but its orientation doesn’t change. Likewise, an object floating in an irrotational vortex would move in a circle without changing its orientation.
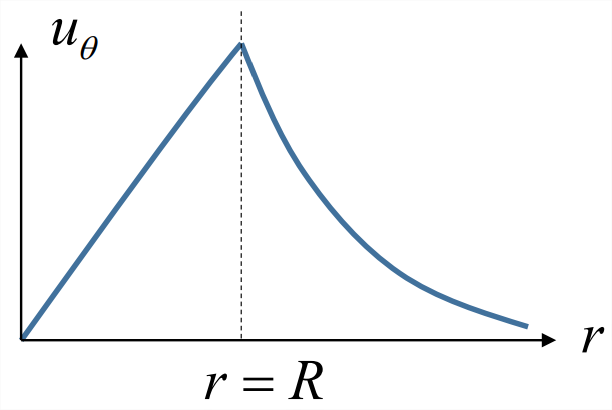
The Rankine vortex
The Rankine vortex3 is a useful model for localized vortices such as tornadoes. The vorticity is uniform out to a radius \(r = R\), and zero (irrotational) beyond that. The azimuthal velocity is sketched in Figure \(\PageIndex{8}\). It is left as an exercise for the student to work out the mathematical expressions for \(u_\theta\) and \(\Gamma\).
Test your understanding by doing problems 24 and 25.

An isolated vortex
Consider the following vorticity distribution, sketched in Figure \(\PageIndex{9}\):
\[\omega=\left\{\begin{array}{cc}
2 \dot{\theta}, & 0 \leq r<R_{1} \\
-2 \dot{\theta}, & R_{1} \leq r \leq R_{2} \\
0, & r>R_{2}
\end{array}\right.\label{eqn:12} \]
where the constant \(\dot{\theta}\) is the angular velocity (i.e. the time derivative of \(\theta\)). On the \(x\) axis, azimuthal velocity is the same as the Cartesian velocity \(v\), and is a maximum at \(r = R_1\). Similarly, on the \(y\) axis, azimuthal velocity is \(u\). From the signs of the derivatives of \(u\) and \(v\), it is easy to see that the vorticity \(\omega = v_x −u_y\) is positive for \(r ≤ R_1\) and negative for \(R_1 < r ≤ R_2\) as in Equation \(\ref{eqn:12}\).
A vortex is called isolated if its total circulation is zero. Here, the total circulation is
\[\Gamma_{\text {total}}=2 \pi \int_{0}^{\infty} \omega\left(r^{\prime}\right) r^{\prime} d r^{\prime} \nonumber \]
can be evaluated for any \(r ≥ R_2\) since there is no vorticity (hence no change in circulation) in that region. The total circulation is zero if \(R_2 = \sqrt{2}R_1\) (check for yourself).
5.3.3 Strain
The strain rate tensor is symmetric by definition:
\[\underset{\sim}{e}=\left[\begin{array}{ccc}
u_{x} & \frac{1}{2}\left(u_{y}+v_{x}\right) & \frac{1}{2}\left(u_{z}+w_{x}\right) \\
\frac{1}{2}\left(u_{y}+v_{x}\right) & v_{y} & \frac{1}{2}\left(v_{z}+w_{y}\right) \\
\frac{1}{2}\left(u_{z}+w_{x}\right) & \frac{1}{2}\left(v_{z}+w_{y}\right) & w_{z}
\end{array}\right].\label{eqn:13} \]
Here, subscripts represent partial derivatives. The diagonal elements of \(\underset{\sim}{e}\), namely \(u_x\), \(v_y\) and \(w_z\), represent normal strain. These can be either extensional or compressive depending on the sign (compare Figures \(\PageIndex{10}\)a,b). Off-diagonal components represent transverse strain, which may also be called tangential strain or shear (Figure \(\PageIndex{10}\)c).
Two points about normal strains are noteworthy.
• Imagine an irrotational straining motion in which the direction of the separation vector between two particles does not change, e.g., the normal strains shown in figures \(\PageIndex{10}\) a and b. The separation vector must be an eigenvector of the strain rate tensor:
\[\frac{d}{d t} \Delta \vec{x}=\Delta \vec{u}=e \Delta \vec{x}=\lambda \Delta \vec{x}. \nonumber \]
The solution of the above is
\[\Delta \vec{x}=\Delta \vec{x}_{0} \exp (\lambda t), \nonumber \]
i.e., the length of the separation vector grows or decays exponentially in time, and the corresponding eigenvalue gives the rate of growth/decay.
• The sum of the normal strains is the trace of the strain rate tensor, which is also equal to the divergence of the velocity field:
\[\operatorname{Tr}(e)=e_{i i}=\frac{\partial u_{i}}{\partial x_{i}}=\vec{\nabla} \cdot \vec{u}.\label{eqn:14} \]
In an incompressible fluid, where \(\vec{\nabla}\cdot\vec{u}=0\), the normal strains must add to zero, i.e., extension and compression balance.


5.3.4 The principal strains
Consider the evolution of a circular distribution of fluid particles advected by a uniformly sheared flow (Figure \(\PageIndex{11}\)), for which the strain is purely transverse (similar to Figure \(\PageIndex{10}\)c). Arrows show the velocity profile, with rightward motion in the upper half of the figure changing linearly to leftward motion in the lower half. As a result, the top of the circle moves to the right, the bottom moves to the left, and the sides don’t move. After a short time, the circle becomes an ellipse with major axis tilted 45 degrees from the horizontal. When viewed in a coordinate frame tilted at the same angle (dashed lines), the circle is being expanded in one direction and compressed in the other. In other words, the transverse strain now appears as a purely normal strain.
This raises a crucial point: the distinction between normal and transverse strains depends on the choice of coordinates. In fact, we will now show that any strain is purely normal in an appropriately chosen coordinate system. Like any second-order tensor, the strain rate tensor can be expressed in a rotated reference frame using the transformation rule Equation 3.3.5:
\[e_{i j}^{\prime}=e_{k l} C_{k i} C_{l j}.\label{eqn:15} \]
Recall that the columns of the rotation matrix \(\underset{\sim}{C}\) are the basis vectors of the rotated coordinate system. Now, suppose that we transform \(\underset{\sim}{e}\) into the special reference frame whose basis vectors are the eigenvectors of \(\underset{\sim}{e}\). Then the \(j^{th}\) column of \(\underset{\sim}{C}\) is the \(j^{th}\) eigenvector:
\[C_{l j}=v_{l}^{(j)},\label{eqn:16} \]
and \(\lambda^{(j)}\) is the corresponding eigenvalue:
\[\left.e_{k l} v_{l}^{(j)}=\lambda^{(j)} v_{k}^{(j)} \quad \text { (no sum on } j\right).\label{eqn:17} \]
Now assume that the eigenvectors have been chosen to be orthogonal with length equal to 1 (and therefore \(v_k^{(I)}v_k^{(j)}=\delta_{ij}\)) and ordered so that \(\det\left(\underset{\sim}{C}\right)=+1\). In other words \(\underset{\sim}{C}\) represents a proper rotation. We now reorder Equation \(\ref{eqn:15}\) and substitute Equation \(\ref{eqn:16}\) and Equation \(\ref{eqn:17}\):
\[e_{i j}^{\prime}=C_{k i} e_{k l} C_{l j}=v_{k}^{(i)} e_{k l} v_{l}^{(j)}=v_{k}^{(i)} \lambda^{(j)} v_{k}^{(j)}=\lambda^{(j)} \delta_{i j} \quad(\text { no sum on } j). \nonumber \]
The result is just a diagonal matrix with the eigenvalue \(\lambda^{(j)}\) as the \(j^{th}\) diagonal element:
\[\underset{\sim}{e^{\prime}}=\left[\begin{array}{ccc}
\lambda^{(1)} & 0 & 0 \\
0 & \lambda^{(2)} & 0 \\
0 & 0 & \lambda^{(3)}
\end{array}\right].\label{eqn:18} \]
This special reference frame is called the principal frame. The basis vectors (the eigenvectors of \(\underset{\sim}{e}\)) are the principal axes of strain and the normal strains appearing on the main diagonal (the eigenvalues of \(\underset{\sim}{e}\)) are the principal strains.
Test your understanding by doing problem 23.
The fine print: In this discussion, we have made two implicit assumptions about the strain rate tensor. First, we have assumed that its eigenvalues and eigenvectors are all real; otherwise, the geometrical interpretation of the principal axes and strains would make no sense. Second, we have assumed that the eigenvectors can be chosen to be orthogonal. Happily, these properties are guaranteed for real, symmetric matrices, of which the strain rate tensor is one. For further details see any linear algebra text (e.g., Bronson and Costa 2009).
1Strain quantifies the net deformation of a material. The strain rate is its time derivative.
2It is only a matter of historical accident that \(e_{ij}\) is defined with the factor 1/2 and \(r_{ij}\) is not.
3William John Macquorn Rankine (1820-1872) was a Scottish engineer whose primary interest was the thermodynamics of steam engines.


