8.2: The Dispersion Relation
- Page ID
- 18082
With \(\rho = \rho_0\) and \(v=\rho=0\), the mass and momentum equations Equations 6.2.5, 6.8.2 are
\[\rho_{0} \frac{D \vec{u}}{D t}=-\rho_{0} g \hat{e}^{(z)}-\vec{\nabla} p.\label{eqn:1} \]
\[\vec{\nabla} \cdot \vec{u}=0\label{eqn:2} \]
The velocity field has components \(u\) and \(w\), and the independent variables are \(x\), \(z\) and \(t\). As in our previous discussion of the baroclinic torque, we separate the pressure into two parts:
\[p=p_{H}+p^{*}, \quad \text { where } \vec{\nabla} p_{H}=-\rho_{0} g \hat{e}^{(z)}, \quad \text { or } p_{H}=-\rho_{0} g z.\label{eqn:3} \]
Note that \(p_H\) is the hydrostatic pressure in the absence of surface deflections. Substituting this decomposition into the momentum equation Equation \(\ref{eqn:1}\) gives
\[\rho_{0} \frac{D \vec{u}}{D t}=-\vec{\nabla} p^{*}.\label{eqn:4} \]
8.2.1 Linearizing the equations of motion
In the absence of motion, the fluid is in an equilibrium state defined by
\[\vec{u}=0, p^{*}=0, \eta=0. \nonumber \]
We will assume that the system remains close to this equilibrium state. As a result of this assumption, any term that involves a product of two or more of \(\vec{u}\), \(p^*\) and \(\eta\) will be treated as negligible. For example:
\[\frac{D \vec{u}}{D t}=\frac{\partial \vec{u}}{\partial t}+\underbrace{[\vec{u} \cdot \vec{\nabla}] \vec{u}}_{\approx 0} \approx \frac{\partial \vec{u}}{\partial t}.\label{eqn:5} \]
As a result, Equation \(\ref{eqn:4}\) becomes
\[\rho_{0} \frac{\partial \vec{u}}{\partial t}=-\vec{\nabla} p^{*}.\label{eqn:6} \]
This equation is linear, and as a result is vastly easier to solve than the nonlinear version Equation \(\ref{eqn:4}\). We must bear in mind, though, that the solution becomes invalid if the amplitude is large enough that the advective term in Equation \(\ref{eqn:5}\) is not negligible. (How large is this? We will take up this important question in section 8.2.4.)
The next step is to derive an equation that we can solve for \(p^*\). Taking the divergence of Equation \(\ref{eqn:6}\) and using \(\ref{eqn:2}\), we find
\[\rho_{0} \vec{\nabla} \cdot \frac{\partial \vec{u}}{\partial t}=\rho_{0} \frac{\partial}{\partial t} \vec{\nabla} \cdot \vec{u}=0=-\vec{\nabla} \cdot \vec{\nabla} p^{*}=-\nabla^{2} p^{*}. \nonumber \]
The nonhydrostatic pressure is therefore a solution of Laplace’s equation:
\[\frac{\partial^{2} p^{*}}{\partial x^{2}}+\frac{\partial^{2} p^{*}}{\partial z^{2}}=0.\label{eqn:7} \]
Combining this with the horizontal and vertical components of Equation \(\ref{eqn:6}\):
\[\rho_{0} \frac{\partial u}{\partial t}=-\frac{\partial p^{*}}{\partial x};\label{eqn:8} \]
\[\rho_{0} \frac{\partial w}{\partial t}=-\frac{\partial p^{*}}{\partial z},\label{eqn:9} \]
we have three equations for the three unknowns \(u\), \(w\), and \(p^*\). Notice further than u appears only in Equation \(\ref{eqn:8}\), so Equation \(\ref{eqn:7}\) and Equation \(\ref{eqn:9}\) form a fully-determined system for the two unknowns \(p^*\) and \(w\).
8.2.2 Boundary conditions
Boundary conditions are imposed at the surface and the bottom. We will begin with the latter as is it is simpler. We assume that the bottom is flat and impermeable:
\[w=0 \quad \text { at } \quad z=-H.\label{eqn:10} \]
Since this is true for all time, it is also true that \(\partial w/\partial t = 0\) at the lower boundary, in which case Equation \(\ref{eqn:9}\) provides a boundary condition on the nonhydrostatic pressure:
\[\frac{\partial p^{*}}{\partial z}=0 \quad \text { at } \quad z=-H.\label{eqn:11} \]
The surface is assumed to be material, i.e., it is always composed of the same fluid particles. As a result:
\[w=\frac{D \eta}{D t} \quad \text { at } \quad z=\eta. \nonumber \]
This boundary condition is both nonlinear and self-referential, i.e., you can’t apply it without knowing \(\eta(x,t)\), which requires knowing the solution. We know how to remove the nonlinearity:
\[\frac{D \eta}{D t}=\frac{\partial \eta}{\partial t}+\underbrace{u \frac{\partial \eta}{\partial x}}_{\approx 0} \approx \frac{\partial \eta}{\partial t}. \nonumber \]
The self-referential nature of the boundary condition is removed via another kind of linearization:
\[\left.w\right|_{z=\eta}=\left.w\right|_{z=0}+\left.\underbrace{\left.\frac{\partial w}{\partial z}\right|_{z=0} \eta}_{\approx 0} \approx w\right|_{z=0}
.\label{eqn:12} \]
The result is a linearized boundary condition:
\[w=\frac{\partial \eta}{\partial t} \quad \text { at } \quad z=0.\label{eqn:13} \]
A second surface condition originates with the requirement that pressure be continuous. The total pressure (\(p_H\) + \(p^*\)) immediately below the water surface must therefore be equal to atmospheric pressure \(p_A\).1 We assume that \(p_A\) is uniform and, since only gradients of pressure matter, we set it to zero. The total pressure \(p\) must therefore approach zero at the surface and, from Equation \(\ref{eqn:3}\),
\[p^{*}=-p_{H}=\rho_{0} g \eta \quad \text { at } \quad z=\eta. \nonumber \]
By the same logic employed in Equation \(\ref{eqn:12}\), we can apply this boundary condition at \(z\) = 0:
\[\left.p^{*}\right|_{z=\eta}=\rho_{0} g \eta=\left.p^{*}\right|_{z=0}+\left.\underbrace{\left.\frac{\partial p^{*}}{\partial z}\right|_{z=0} \eta}_{\approx 0} \approx p^{*}\right|_{z=0}, \nonumber \]
and therefore
\[p^{*}=\rho_{0} g \eta \quad \text { at } \quad z=0.\label{eqn:14} \]
Taking inventory: Our problem now consists of the equations Equation \(\ref{eqn:7}\) and Equation \(\ref{eqn:9}\) and the boundary conditions Equation \(\ref{eqn:10}\), Equation \(\ref{eqn:11}\), Equation \(\ref{eqn:13}\) and Equation \(\ref{eqn:14}\). Once these are solved for \(p^∗\) and \(w\), the horizontal momentum equation Equation \(\ref{eqn:8}\) can be solved separately to obtain \(u\).
8.2.3 The normal mode solution
We are looking for solutions for the nonhydrostatic pressure \(p^∗\) and the vertical velocity \(w\). To begin with, we will seek a solution in which \(p^∗\) has the following form:
\[p^{*}=P(z) \cos (k x-\omega t).\label{eqn:15} \]
This is called a normal mode or a plane wave solution. Several features of this important functional form should be noted.
- \(P(z)\) is a function yet to be determined
- The \(x\)-dependence is determined by the \(x\)-wavenumber \(k\), which is also equal to \(2\pi/\lambda\), \(\lambda\) being the wavelength.
- The time-dependence is described by the radian frequency \(\omega\), which is related to the period \(T\) by \(\omega = 2\pi/T\). It is often more convenient to use the cyclic frequency \(f=\omega/2\pi\), with units of cycles per second (cps.) or Hertz (Hz.)
- The pattern moves with phase speed \(c=\omega/k\).
The assumption Equation \(\ref{eqn:15}\) is not as restrictive as it may appear at first. By virtue of Fourier’s theorem (see any applied math text), an arbitrary dependence on \(x\) and \(t\) can be expressed as a superposition of trigonometric functions of the form Equation \(\ref{eqn:15}\). Moreover, because the equations are linear, if Equation \(\ref{eqn:15}\) is a solution, any such superposition will also be a solution.
Substituting Equation \(\ref{eqn:15}\) into Equation \(\ref{eqn:7}\), we have
\[\frac{\partial^{2} p^{*}}{\partial x^{2}}+\frac{\partial^{2} p^{*}}{\partial z^{2}}=\left[-k^{2} P+P^{\prime \prime}\right] \cos (k x-\omega t)=0, \nonumber \]
where primes denote derivatives with respect to \(z\). Because the last equality must be valid for all \(x\) and \(t\), the quantity in square brackets must be zero:
\[P^{\prime \prime}=k^{2} P. \nonumber \]
This is a very common ordinary differential equation whose solutions can be expressed in terms of hyperbolic functions. To satisfy the bottom boundary condition Equation \(\ref{eqn:11}\), we choose
\[P=P_{0} \cosh k(z+H)\label{eqn:16} \]
where \(P_0\) is an undetermined constant
Next we need a corresponding solution for \(w\). In the vertical momentum equation Equation \(\ref{eqn:9}\) we try a solution of the form
\[w=W(z) \sin (k x-\omega t).\label{eqn:17} \]
This results in
\[-\rho_{0} \omega W \cos (k x-\omega t)=-P^{\prime} \cos (k x-\omega t). \nonumber \]
Since this must be true for all \(x\) and \(t\), the coefficients of the cosine functions must be equal. Therefore Equation \(\ref{eqn:17}\) is a solution provided that:
\[W=\frac{P^{\prime}}{\rho_{0} \omega}, \nonumber \]
or, substituting Equation \(\ref{eqn:16}\),
\[W=\frac{P_{0} k}{\rho_{0} \omega} \sinh k(z+H).\label{eqn:18} \]
Note that Equation \(\ref{eqn:18}\) automatically satisfies Equation \(\ref{eqn:10}\), the bottom boundary condition on \(w\). In summary, we now have solutions for \(p^*\) and \(w\) in the form of Equation \(\ref{eqn:15}\), Equation \(\ref{eqn:16}\), Equation \(\ref{eqn:17}\), and Equation \(\ref{eqn:18}\), and these satisfy the bottom boundary conditions Equation \(\ref{eqn:11}\) and Equation \(\ref{eqn:10}\).
To satisfy the surface boundary conditions Equation \(\ref{eqn:13}\) and Equation \(\ref{eqn:14}\), we must consider the surface deflection \(\eta(x,t)\). Equation \(\ref{eqn:14}\) requires \(p^*=\rho_0gn\) at \(z\) = 0. We solve for \(\eta\) and substitute Equation \(\ref{eqn:15}\) and Equation \(\ref{eqn:16}\) to get
\[\eta=\frac{1}{\rho_{0} g} P_{0} \cosh k H \cos (k x-\omega t). \nonumber \]
Since the surface deflection is easier to observe than the pressure, we will rewrite this solution as
\[\eta=\eta_{0} \cos (k x-\omega t),\label{eqn:19} \]
and note that \(P_0=\rho_0g\eta_0/\cosh kH\). Our solutions Equation \(\ref{eqn:16}\) and \(\ref{eqn:18}\) for \(P\) and \(W\) become
\[P=\rho_{0} g \eta_{0} \frac{\cosh k(z+H)}{\cosh k H};\label{eqn:20} \]
and
\[W=\frac{g k}{\omega} \eta_{0} \frac{\sinh k(z+H)}{\cosh k H}.\label{eqn:21} \]
We now have a complete solution for \(p^*\), \(w\) and \(\eta\), but we have not yet satisfied Equation \(\ref{eqn:13}\), the surface condition on \(w\), i.e., we have an overdetermined system. The solution can only work for certain combinations of the wave parameters \(k\) and \(\omega\). Substituting our solutions Equation \(\ref{eqn:19}\) and Equation \(\ref{eqn:21}\) into Equation \(\ref{eqn:13}\), we have
\[\frac{g k}{\omega} \eta_{0} \frac{\sinh k H}{\cosh k H} \sin (k x-\omega t)=\eta_{0} \omega \sin (k x-\omega t) \quad \forall x, t, \nonumber \]
and thus
\[\frac{g k}{\omega} \eta_{0} \frac{\sinh k H}{\cosh k H}=\eta_{0} \omega, \nonumber \]
or
\[\omega^{2}=g k \tanh k H.\label{eqn:22} \]
This is called the dispersion relation. The normal mode expressions Equation \(\ref{eqn:15}\), Equation \(\ref{eqn:17}\), and Equation \(\ref{eqn:19}\) can satisfy the equations and all of the boundary conditions only if \(\omega\) and \(k\) satisfy Equation \(\ref{eqn:22}\).
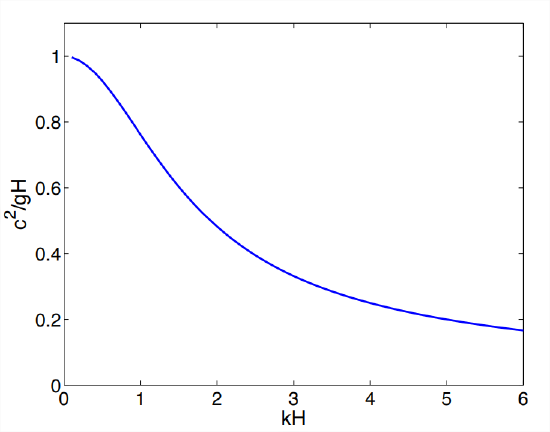
We can gain some insight into the propagation of surface gravity waves by writing the dispersion relation in terms of the phase speed \(c=\omega/k\):
\[c^{2}=\frac{g}{k} \tanh k H=g H \frac{\tanh k H}{k H},\label{eqn:23} \]
as shown in Figure \(\PageIndex{2}\). The fastest propagation occurs when \(kH\) is small, i.e., in the limit of low wavenumber, or wavelength long compared to the water depth. This is in contrast to sound waves, in which the short waves travel fastest. (Imagine, for example, the sound of thunder. It begins with a high-frequency clap, then decays away to a low-frequency rumble.) In the ocean, surface waves are most often generated by storms. An observer some distance from the storm will see long, low-frequency waves first.
Test your understanding: In exercise 33 you will extend this derivation to include the effects of surface tension.
To complete the picture of small-amplitude surface waves, we now go back and add the horizontal velocity \(u\). This is easily done by substituting our solution Equation \(\ref{eqn:15}\) and Equation \(\ref{eqn:20}\) into the horizontal momentum equation Equation \(\ref{eqn:8}\). This results in
\[u=U(z) \cos (k x-\omega t),\label{eqn:24} \]
where
\[U(z)=\frac{g k}{\omega} \eta_{0} \frac{\cosh k(z+H)}{\cosh k H}.\label{eqn:25} \]
We can write this in a slightly more intuitive form if we note that (1) the dispersion relation Equation \(\ref{eqn:22}\) can be rearranged to give \(kg/\omega=\omega/\tanh kH\) and (2) \(\cosh x\tanh x = \sinh x\), and therefore
\[U(z)=\omega \eta_{0} \frac{\cosh k(z+H)}{\sinh k H}.\label{eqn:26} \]
The velocity profile rises from a minimum value at the bottom to a maximum at the surface. Similarly, Equation \(\ref{eqn:21}\) can be rewritten as
\[W(z)=\omega \eta_{0} \frac{\sinh k(z+H)}{\sinh k H},\label{eqn:27} \]
which rises from zero at the bottom to the maximum value \(\omega\eta_0\) at the surface.
8.2.4 How small is small?
The solution derived above depends on the assumption that the amplitude of the waves is “small”. How large can the amplitude be before this assumption is violated? It depends on how much inaccuracy we can tolerate. As a general introduction to the way theorists think about such questions, let us make order-of-magnitude estimates of the two terms in the material derivative of \(\vec{u}\) cf. Equation \(\ref{eqn:5}\). Suppose we are dealing with waves having period \(T\), wavelength \(\lambda\) and velocity amplitude \(u_0\). We estimate the time derivative as \(u_0/T\) and the space derivative as \(u_0/\lambda\), leading to:
\[\frac{\partial \vec{u}}{\partial t} \approx \frac{u_{0}}{T} ; \quad[\vec{u} \cdot \vec{\nabla}] \vec{u} \approx \frac{u_{0}^{2}}{\lambda}.\label{eqn:28} \]
We then require that the second term be much smaller than the first, which is equivalent to
\[u_{0} \ll \lambda / T \nonumber \]
In other words, the maximum fluid velocity should be much smaller than the phase speed of the waves.
8.2.5 Particle paths
Suppose that, in the absence of waves, a fluid particle is located at \(\vec{x}_0\), and in the presence of waves its position is \(\vec{x}_0+\vec{x}^\prime(t)\). The particle’s motion is described by
\[\frac{d \vec{x}^{\prime}}{d t}=\vec{u}\left(\vec{x}_{0}, t\right) \nonumber \]
recognising that the difference between \(\vec{u}(\vec{x}_0,t)\) and \(\vec{u}(\vec{x},t)\) is negligible.
Having solved for the components of \(\vec{u}\) Equation \(\ref{eqn:24}\), Equation \(\ref{eqn:26}\), Equation \(\ref{eqn:17}\), and Equation \(\ref{eqn:27}\), we can substitute the results and integrate in time to obtain the trajectory of the particle. The result is
\[x^{\prime}=-\frac{U\left(z_{0}\right)}{\omega} \sin \left(k x_{0}-\omega t\right) ; \quad z^{\prime}=\frac{W\left(z_{0}\right)}{\omega} \cos \left(k x_{0}-\omega t\right).\label{eqn:29} \]
We can rewrite this as
\[\frac{x^{\prime 2}}{L_{x}^{2}}+\frac{z^{\prime 2}}{L_{z}^{2}}=1,\label{eqn:30} \]
where
\[L_{x}=\eta_{0} \frac{\cosh k\left(z_{0}+H\right)}{\sinh k H} ; \quad L_{z}=\eta_{0} \frac{\sinh k\left(z_{0}+H\right)}{\sinh k H}.\label{eqn:31} \]
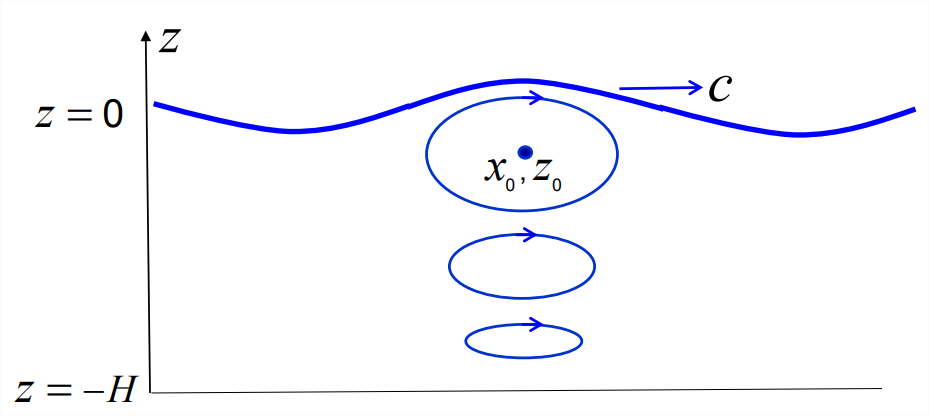
We can now make three observations about the particle paths.
- Each path is an ellipse with radii \(L_x\) and \(L_z\) (Figure \(\PageIndex{3}\)). Both \(L_x\) and \(L_z\) decrease with depth, with \(L_z\) = 0 at the bottom (where \(z_0\) = −H).
- The vertical excursion \(z^\prime\) is proportional to the surface deflection cf. Equation \(\ref{eqn:19}\):\[z^{\prime}=\eta(x, t) \frac{\sinh k\left(z_{0}+H\right)}{\sinh k H}, \nonumber \] and therefore reaches a maximum directly beneath the wave crests for all \(z_0\).
- The horizontal particle velocity is also proportional to \(\eta\): \[u=\frac{g}{c} \eta(x, t) \frac{\cosh k\left(z_{0}+H\right)}{\cosh k H}, \nonumber \] where Equation \(\ref{eqn:25}\) and the definition of the phase velocity \(c=\omega/k\) have been used. Its value at \(z\) = 0 is \[u=\frac{g}{c} \eta(x, t). \nonumber \] Directly beneath the wave crests, the horizontal motion has the same sign as the phase speed.
If we extend the theory to take nonlinear effects into account, we find that there is actually a slight drift in the direction of the wave propagation. Called the Stokes drift, it results from the fact that the particle speed at the top of each ellipse is slightly greater than the speed at the bottom of the ellipse. Appendix J gives a more detailed discussion.
1If centimeter-scale waves are of interest, we must also take account of surface tension. The force that holds water molecules together is stronger on the water side than on the air side, creating an additional pressure at the surface given by \(p=-\sigma\nabla^2\eta\), where \(\sigma\) is a constant and small amplitude is assumed. You will examine this effect in homework problem 33.


