17.2: F.2 Stress on a tilted plane
- Page ID
- 18114
Consider a plane of arbitrary orientation as shown in Figure \(\PageIndex{1}\). The intersection of the tilted plane with the coordinate planes forms a tetrahedron. The tilted surface, outlined in red, is called the hypotenuse of the tetrahedron. We will first find an expression for the force acting on each face of the tetrahedron. We will then argue that this total force must vanish as the tetrahedron shrinks to infinitesimal size. Therefore, the force on the hypotenuse must balance the sum of the forces on the other surfaces.
Each of the coordinate faces has outward unit normal opposite to the corresponding basis vector. For example, the face labelled \(A^{(1)}\) has outward unit normal \(−\hat{e}^{(1)}\). Therefore, the stresses acting on those faces are minus the corresponding elements of the Cauchy array. The net force is the sum of the stress vectors times the areas of the faces act upon:
\[\vec{F}=\vec{f} A-\tau_{i j} \hat{e}^{(j)} A^{(i)}.\label{eqn:1} \]
We now assume that the tetrahedon is filled with a continuous medium of density \(\rho\). By Newton’s second law, the sum of forces equals the product of the mass of the tetrahedron, \(m\), and resultant acceleration \(\vec{a}\). Taking the \(j\) component, we have
\[f_{j} A-\tau_{i j} A^{(i)}=m a_{j}.\label{eqn:2} \]
To proceed, we need two facts from three-dimensional geometry that may be unfamiliar:
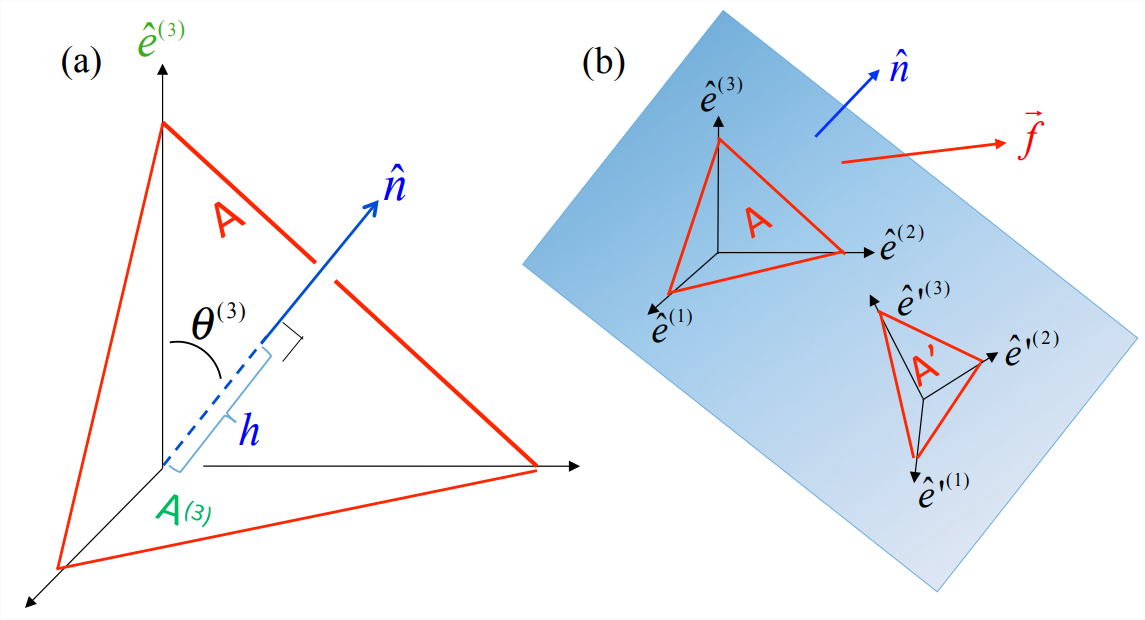
- . The volume of a tetrahedron is \(Ah/3\), where \(A\) is the area of the hypotenuse and \(h\) is the perpendicular distance from the hypotenuse to the origin (Figure \(\PageIndex{2}\)a). This is analogous to the formula for the area of a triangle: one half the base times the height. The mass is therefore \[m=\rho A h / 3.\label{eqn:3} \]
- The area of each of the orthogonal coordinate planes is proportional to the area of the hypotenuse: \[A^{(i)}=A \cos \theta^{(i)}. \nonumber \] Here, \(\theta^{(i)}\) is the angle between \(\hat{e}^{(i)}\) and \(\hat{n}\), \(\hat{n}\) being the outward unit normal to the tilted surface. (Figure \(\PageIndex{2}\) shows the example \(i\) = 3.) This may be understood by recognizing that \(\theta^{(i)}\) is the angle between the two planes, and the projection of the hypotenuse onto the coordinate plane is \(A\) times cosine of that angle. The cosine can also be expressed as the component of \(\hat{n}\) perpendicular to the coordinate plane. To see this, note that the dot product of \(\hat{n}\) and \(\hat{e}^{(i)}\) is the product of their magnitudes (both equal to one) times \(\cos\theta^{(i)}\). Moreover, that dot product is also equal to the \(i\) component of \(\hat{n}\), so \(\cos\theta^{(i)}\) = \(n_i\). As a result, we have \[A^{(i)}=A n_{i}.\label{eqn:4} \]
Substituting Equation \(\ref{eqn:3}\) and Equation \(\ref{eqn:4}\) into Equation \(\ref{eqn:2}\), we obtain
\[f_{j} A-\tau_{i j} A n_{i}=\rho A \frac{h}{3} a_{j}, \nonumber \]
or
\[f_{j}-\tau_{i j} n_{i}=\rho \frac{h}{3} a_{j}. \nonumber \]
We now shrink the size of the tetrahedron to zero by taking the limit \(h\rightarrow 0\), resulting in
\[f_{j}=\tau_{i j} n_{i}.\label{eqn:5} \]
From the foregoing, we can conclude that \(\underset{\sim}{\tau}\) is a tensor. This can be seen in two ways.
- In deriving Equation \(\ref{eqn:5}\), we did not assume a specific coordinate system; any Cartesian coordinate system would do. Referring to figure (Figure \(\PageIndex{2}\)b), if we rotated the coordinate axes (keeping the tilted plane fixed), the areas \(A\) and \(A^{(i)}\) would change, as would the values of the \(\tau_{i j}\), but we would still arrive at Equation \(\ref{eqn:5}\).
- Both \(\vec{f}\) and \(\vec{n}\) are vectors, since they exist in physical space independently of the coordinate system. Therefore \(\underset{\sim}{\tau}\), as a relationship between two vectors, must transform as a second order tensor (section 3.3.1).
We therefore refer to \(\tau\) as the Cauchy stress tensor, or just the stress tensor. While the stress vector \(\vec{f}(\vec{x},t,\hat{n})\) depends on the orientation of the plane it acts on, the stress tensor depends only on location and time: \(\tau = \tau (\vec{x},t)\). It contains the information needed to evaluate the stress vector acting on any plane passing through \(\vec{x}\).