7.5: A Head Loss Model for Heterogeneous Slurry Transport
- Page ID
- 29231
7.5.1 Introduction
Most well-known head loss equations for heterogeneous transport, Durand & Condolios (1952), Fuhrboter (1961), Newitt et al. (1955), Jufin & Lopatin (1966) and Wilson et al. (1992) are based on a single excess pressure term for the solids effect. This term is usually based on curve fitting, some physics or dimensionless numbers. The main question is, can the excess pressure (the solids effect) accurately be described by just one term and if so, does this term depend on the hydraulic gradient of the carrier liquid or is it independent. The model as derived here is based on the assumption that the excess hydraulic gradient is the result of energy losses. These energy losses are identified as potential energy losses and kinetic energy losses. One could distinguish more types of energy losses and maybe come with a more accurate equation, but the current approach already gives a good correlation with the data of many researchers. The potential energy losses are dominated by the terminal settling velocity of the particles, including hindered settling. The kinetic energy losses are dominated by the ratio between the slip velocity of the particles and the terminal settling velocity of the particles (without hindered settling). The slip velocity cannot be derived fundamentally (yet), but is approximated by a function with the dimension of velocity. The final result is an equation with 3 independent terms. The viscous friction losses according to Darcy Weisbach, using the Moody diagram for the friction coefficient, the potential energy losses, using an approach similar to Newitt et al. (1955) and the kinetic energy losses as derived in this chapter.
7.5.2 Physical Energy Considerations
To give some direction to the form of the semi-empirical equations, a simple power/energy balance will be derived (see Miedema &Ramsdell (2013)). Assuming that the additional pressure resulting from the solids in the liquid is the result of the energy required to keep the particles in suspension and take the losses of kinetic energy in to account, the following theory can be derived, starting with potential energy losses:
Potential Energy
The power ΔPs, pot required to pump the solids/liquid mixture over a distance ΔL because of the constant loss of potential energy, is the result of the pressure difference Δps, pot times the cross-section of the pipe Ap times the line speed vls.
\[\ \Delta \mathrm{P}_{\mathrm{s}, \mathrm{p o t}}=\Delta \mathrm{p}_{\mathrm{s}, \mathrm{p o t}} \cdot \mathrm{A}_{\mathrm{p}} \cdot \mathrm{v}_{\mathrm{l} \mathrm{s}}\]
The potential energy of 1 particle at a factor κC times half the pipe diameter is (the eccentricity factor), assuming that on average particles are located at a distance κC·Dp/2 from the bottom of the pipe, with κC<1:
\[\ \Delta \mathrm{E}_{\mathrm{s}, \mathrm{pot}}=\mathrm{m}_{\mathrm{p}} \cdot \mathrm{g} \cdot \kappa_{\mathrm{C}} \cdot \frac{\mathrm{D}_{\mathrm{p}}}{2}=\left(\rho_{\mathrm{s}}-\rho_{\mathrm{l}}\right) \cdot \frac{\pi}{6} \cdot \mathrm{d}^{3} \cdot \mathrm{g} \cdot\left(\mathrm{\kappa}_{\mathrm{C}} \cdot \frac{\mathrm{D}_{\mathrm{p}}}{2}\right)\]
The number of particles in a pipeline with length ΔL is:
\[\ \mathrm{n=\frac{A_{p} \cdot \Delta L \cdot C_{v s}}{\frac{\pi}{6} \cdot d^{3}}}\]
The potential energy ΔEs,pot,tot available in the solid/liquid mixture over a distance ΔL, assuming the particles are at a distance κC·Dp/2 from the bottom of the pipe is now:
\[\ \Delta \mathrm{E}_{\mathrm{s}, \mathrm{p o t}, \mathrm{t o t}}=\mathrm{n} \cdot \Delta \mathrm{E}_{\mathrm{s}, \mathrm{p} \mathrm{o t}}=\mathrm{A}_{\mathrm{p}} \cdot \Delta \mathrm{L} \cdot \mathrm{C}_{\mathrm{v s}} \cdot\left(\rho_{\mathrm{s}}-\rho_{\mathrm{l}}\right) \cdot \mathrm{g} \cdot\left(\mathrm{\kappa}_{\mathrm{C}} \cdot \frac{\mathrm{D}_{\mathrm{p}}}{\mathrm{2}}\right)\]
The time Δt required for the settling of the particles, based on the average location at a distance κC·Dp/2 from the bottom of the pipe is (including the effect of hindered settling, here Richardson & Zaki (1954) is used):
\[\ \Delta \mathrm{t}=\frac{\left(\mathrm{\kappa}_{\mathrm{C}} \cdot \frac{\mathrm{D}_{\mathrm{p}}}{\mathrm{2}}\right)}{\mathrm{v}_{\mathrm{t}} \cdot\left(\mathrm{1}-\frac{\mathrm{C}_{\mathrm{v s}}}{\mathrm{\kappa}_{\mathrm{C}}}\right)^{\beta}}\]
If κC<1, the concentration Cvs is not evenly distributed over the height of the pipe and will be higher in the bottom of the pipe. This is taken into account by dividing the average concentration by κC. So the power required to keep the particles in suspension, is equal to the potential energy ΔEpot, tot, divided by the time Δt required to move from the center of the pipe to the bottom is:
\[\ \frac{\Delta \mathrm{E}_{\mathrm{s}, \mathrm{p} \mathrm{o} \mathrm{t}, \mathrm{to} \mathrm{t}}}{\Delta \mathrm{t}}=\mathrm{A}_{\mathrm{p}} \cdot \Delta \mathrm{L} \cdot \mathrm{C}_{\mathrm{v} \mathrm{s}} \cdot\left(\rho_{\mathrm{s}}-\rho_{\mathrm{l}}\right) \cdot \mathrm{g} \cdot \mathrm{v}_{\mathrm{t}} \cdot\left(\mathrm{1}-\frac{\mathrm{C}_{\mathrm{v s}}}{\mathrm{\kappa}_{\mathrm{C}}}\right)^{\beta}\]
Equation (7.5-1) and (7.5-6) should be equal, resulting in a required pressure gradient of:
\[\ \frac{\Delta \mathrm{p}_{\mathrm{s}, \mathrm{p} \mathrm{o t}}}{\Delta \mathrm{L}}=\frac{\mathrm{C}_{\mathrm{v} \mathrm{s}} \cdot\left(\rho_{\mathrm{s}}-\rho_{\mathrm{l}}\right) \cdot \mathrm{g} \cdot \mathrm{v}_{\mathrm{t}} \cdot\left(\mathrm{1}-\frac{\mathrm{C}_{\mathrm{v} \mathrm{s}}}{\mathrm{\kappa}_{\mathrm{C}}}\right)^{\beta}}{\mathrm{v}_{\mathrm{l} \mathrm{s}}}\]
In terms of the solids effect due to potential energy is,pot on the hydraulic gradient i this gives:
\[\ \mathrm{i}_{\mathrm{s}, \mathrm{pot}}=\frac{\Delta \mathrm{p}_{\mathrm{s}, \mathrm{pot}}}{\rho_{\mathrm{l}} \cdot \mathrm{g} \cdot \Delta \mathrm{L}}=\frac{\mathrm{v}_{\mathrm{t}} \cdot\left(1-\frac{\mathrm{C}_{\mathrm{vs}}}{\mathrm{\kappa}_{\mathrm{C}}}\right)^{\beta}}{\mathrm{v}_{\mathrm{ls}}} \cdot \mathrm{R}_{\mathrm{sd}} \cdot \mathrm{C}_{\mathrm{vs}}\]
In terms of the relative excess hydraulic gradient component due to potential energy losses Shr (Settling velocity Hindered Relative), this gives the ratio between the hindered settling velocity in the lower part of the pipe to the line speed:
| \[\ \mathrm{S}_{\mathrm{hr}}=\frac{\mathrm{i}_{\mathrm{s}, \mathrm{p o t}}}{\mathrm{R}_{\mathrm{s d}} \cdot \mathrm{C}_{\mathrm{v s}}}=\frac{\mathrm{v}_{\mathrm{t}} \cdot\left(\mathrm{1}-\frac{\mathrm{C}_{\mathrm{v s}}}{\mathrm{\kappa}_{\mathrm{C}}}\right)^{\beta}}{\mathrm{v}_{\mathrm{l s}}}\] |
The factor κC will have a value smaller or equal to 1, depending on the asymmetry of the concentration profile over the vertical in the pipe. If this concentration profile is symmetrical, a value of 1 should be used. However in general in heterogeneous transport the concentration in the bottom half of the pipe will be higher than in the top half. If 100% of the particles would be in the lower half of the pipe, a factor of 1⁄2 should be used, but this is seldom the case. A factor of 2/3 or 4/5 seems to be more reasonable. The smaller this factor, the smaller the potential energy losses.
Substituting the equation for the liquid resistance Δpl gives:
\[\ \Delta \mathrm{p}_{\mathrm{m}}=\Delta \mathrm{p}_{\mathrm{l}}+\Delta \mathrm{p}_{\mathrm{s}, \mathrm{p o t}}=\Delta \mathrm{p}_{\mathrm{l}} \cdot\left(\mathrm{1}+\frac{\Delta \mathrm{p}_{\mathrm{s}, \mathrm{p} \mathrm{o t}}}{\Delta \mathrm{p}_{\mathrm{l}}}\right)=\Delta \mathrm{p}_{\mathrm{l}} \cdot\left(\mathrm{1}+\mathrm{\Phi} \cdot \mathrm{C}_{\mathrm{v} \mathrm{s}}\right)\]
In terms of the hydraulic gradient this can also be written as:
\[\ \mathrm{i}_{\mathrm{m}}=\mathrm{i}_{\mathrm{l}}+\mathrm{i}_{\mathrm{s}, \mathrm{p} \mathrm{o t}}=\mathrm{i}_{\mathrm{l}} \cdot\left(\mathrm{1}+\frac{\mathrm{i}_{\mathrm{s}, \mathrm{p} \mathrm{o t}}}{\mathrm{i}_{\mathrm{l}}}\right)=\mathrm{i}_{\mathrm{l}} \cdot\left(\mathrm{1}+\mathrm{\Phi} \cdot \mathrm{C}_{\mathrm{v s}}\right)\]
According to equation (7.5-7) the extra pressure losses due to the potential energy losses of the solids is proportional to the volumetric concentration Cvs, the submerged density of the solids (ρs-ρl), the terminal settling velocity of the particles vt and inversely proportional with the line speed vls. The terminal settling velocity vt however is influenced by hindered settling (using Richardson & Zaki (1954)), while the friction factor λl is influenced by the Reynolds number Re of the flow in the pipe according to Moody diagram. This results in:
\[\ \Phi=2 \cdot \frac{\left(\mathrm{g} \cdot \mathrm{D}_{\mathrm{p}} \cdot \mathrm{R}_{\mathrm{sd}}\right) \cdot \mathrm{v}_{\mathrm{t}} \cdot\left(1-\frac{\mathrm{C}_{\mathrm{vs}}}{\mathrm{\kappa}_{\mathrm{C}}}\right)^{\beta}}{\lambda_{\mathrm{l}}(\mathrm{Re})} \cdot\left(\frac{1}{\mathrm{v}_{\mathrm{ls}}}\right)^{3}\]
The power β is a function of the particle Reynolds number \(\ \frac{\mathrm{v}_{\mathrm{t}} \cdot \mathrm{d}}{v_{\mathrm{l}}}\), while the friction factor λl is a weak function of the Reynolds number of the flow in the pipe \(\ \frac{\mathrm{v}_{\mathrm{ls}} \cdot \mathrm{D}_{\mathrm{p}}}{v_{\mathrm{l}}}\). Equation (7.5-10) can also be written as:
\[\ \Delta \mathrm{p}_{\mathrm{m}}=\Delta \mathrm{p}_{\mathrm{l}} \cdot\left(1+2 \cdot \Omega \cdot\left(\frac{1}{\mathrm{v}_{\mathrm{l s}}}\right)^{3}\right) \quad\text{ with: }\quad \Omega=\frac{\left(\mathrm{g} \cdot \mathrm{D}_{\mathrm{p}} \cdot \mathrm{R}_{\mathrm{s d}}\right) \cdot \mathrm{v}_{\mathrm{t}} \cdot\left(\mathrm{1}-\frac{\mathrm{C}_{\mathrm{v} \mathrm{s}}}{\mathrm{\kappa}_{\mathrm{C}}}\right)^{\beta}}{\lambda_{\mathrm{l}}(\mathrm{R} \mathrm{e})} \cdot \mathrm{C}_{\mathrm{v} \mathrm{s}}\]
Taking the derivative of equation (7.5-13) with respect to the line speed vls and making the derivative equal to 0 to find the minimum, results in a minimum at a line speed of:
\[\ \begin{array}{left} \mathrm{v}_{\mathrm{l s}, \min }=\Omega^{1 / 3}=\left(\frac{\left(\mathrm{g} \cdot \mathrm{D}_{\mathrm{p}} \cdot \mathrm{R}_{\mathrm{s} \mathrm{d}}\right) \cdot \mathrm{v}_{\mathrm{t}} \cdot\left(\mathrm{1}-\frac{\mathrm{C}_{\mathrm{v s}}}{\mathrm{\kappa}_{\mathrm{C}}}\right)^{\beta}}{\lambda_{\mathrm{l}}(\mathrm{R} \mathrm{e})} \cdot \mathrm{C}_{\mathrm{v s}}\right)^{1 / \mathrm{3}}\\
\Delta\mathrm{p_{m,min=3\cdot \Delta p_l}}
\end{array}
\]
So the minimum resistance equals 3 times the water resistance. Equations (7.5-10) and (7.5-13) are based on some assumptions and give an idea of what resistance equation could look like. In fact these equations are very similar to the Newitt et al. (1955) equation, except for the fact that hindered settling is taken into account. For a λl value of 0.02 (high Reynolds number, smooth pipe, small pipe diameter) a factor of 100 is found for 2/λl, while Newitt et al. (1955) found a factor of 1100, which is 11 times as much as the theoretical value if hindered settling is not taken into account. Now Newitt et al. (1955) tried to explain all the excess losses being potential energy losses with a low efficiency for the potential energy. A factor of 11 without hindered settling and an even much higher factor if hindered settling is included can hardly be explained by some efficiency factor. Apparently the loss of potential energy only explains part of the pressure losses. The other part of the pressure losses will be explained by the loss of kinetic energy.
Kinetic Energy
The power ΔPs, kin required to pump the solids/liquid mixture over a distance ΔL because of the constant loss of kinetic energy due to impact of the particles with the wall and due to acceleration and deceleration in eddies, is the result of the pressure difference Δps, kin times the cross-section of the pipe Ap times the line speed vls.
\[\ \Delta \mathrm{P}_{\mathrm{s}, \mathrm{k i n}}=\Delta \mathrm{p}_{\mathrm{s}, \mathrm{k i n}} \cdot \mathrm{A}_{\mathrm{p}} \cdot \mathrm{v}_{\mathrm{l} \mathrm{s}}\]
The slip velocity vsl is defined as the difference between the average liquid velocity vl and the average particle velocity vp resulting in a drag force.
\[\ \mathrm{v}_{\mathrm{s l}}=\mathrm{v}_{\mathrm{l}}-\mathrm{v}_{\mathrm{p}}\]
The volume flow of mixture Qm is equal to the volume flow of liquid Ql plus the volume flow of particles Qp, thus:
\[\ \mathrm{Q}_{\mathrm{m}}=\mathrm{Q}_{\mathrm{l}}+\mathrm{Q}_{\mathrm{p}} \quad \Rightarrow \quad \mathrm{A}_{\mathrm{p}} \cdot \mathrm{v}_{\mathrm{l} \mathrm{s}}=\mathrm{A}_{\mathrm{p}} \cdot\left(\mathrm{1}-\mathrm{C}_{\mathrm{v s}}\right) \cdot \mathrm{v}_{\mathrm{l}}+\mathrm{A}_{\mathrm{p}} \cdot \mathrm{C}_{\mathrm{v s}} \cdot \mathrm{v}_{\mathrm{p}}\]
Giving:
\[\ \mathrm{v}_{\mathrm{l s}}=\mathrm{v}_{\mathrm{l}}+\mathrm{C}_{\mathrm{v s}} \cdot\left(\mathrm{v}_{\mathrm{p}}-\mathrm{v}_{\mathrm{l}}\right)=\mathrm{v}_{\mathrm{l}}-\mathrm{C}_{\mathrm{v s}} \cdot \mathrm{v}_{\mathrm{sl}}\]
The liquid velocity vl is higher than the line speed vls. As we will see later, the slip velocity vsl is much smaller than the line speed vls and in general this effect can be neglected. Only at very small line speeds, at high concentrations and with large particles, the equations derived may need a correction. However this will in general be far below the Limit Deposit Velocity vls,ldv, while here heterogeneous transport is considered.
\[\ \mathrm{v}_{\mathrm{l}}=\mathrm{v}_{\mathrm{l} \mathrm{s}}+\mathrm{C}_{\mathrm{v s}} \cdot \mathrm{v}_{\mathrm{s} \mathrm{l}}\]
Suppose particles hit the wall or interact with eddies and loose some of their speed, let’s say by a value vsl, the slip velocity. The kinetic energy lost by the particle is now:
\[\ \begin{array}{left}\Delta \mathrm{E}_{\mathrm{s}, \mathrm{k i n}, \mathrm{p}}=\frac{\mathrm{1}}{2} \cdot \mathrm{m}_{\mathrm{p}} \cdot \mathrm{v}_{\mathrm{l}}^{2}-\frac{\mathrm{1}}{2} \cdot \mathrm{m}_{\mathrm{p}} \cdot\left(\mathrm{v}_{\mathrm{l}}-\mathrm{v}_{\mathrm{s l}}\right)^{2}=\frac{\mathrm{1}}{2} \cdot \mathrm{m}_{\mathrm{p}} \cdot\left(\mathrm{2} \cdot \mathrm{v}_{\mathrm{l}} \cdot \mathrm{v}_{\mathrm{s} \mathrm{l}}-\mathrm{v}_{\mathrm{s l}}^{2}\right)\\
\Delta \mathrm{E}_{\mathrm{s}, \mathrm{k i n}, \mathrm{p}}=\frac{1}{2} \cdot \mathrm{m}_{\mathrm{p}} \cdot\left(2 \cdot\left(\mathrm{v}_{\mathrm{l} \mathrm{s}}+\mathrm{C}_{\mathrm{v} \mathrm{s}} \cdot \mathrm{v}_{\mathrm{s} \mathrm{l}}\right) \cdot \mathrm{v}_{\mathrm{s} \mathrm{l}}-\mathrm{v}_{\mathrm{s} \mathrm{l}}^{2}\right)=\frac{1}{2} \cdot \mathrm{m}_{\mathrm{p}} \cdot\left(\mathrm{2} \cdot \mathrm{v}_{\mathrm{ls}} \cdot \mathrm{v}_{\mathrm{sl}}+\left(\mathrm{2} \cdot \mathrm{C}_{\mathrm{v} \mathrm{s}}-\mathrm{1}\right) \cdot \mathrm{v}_{\mathrm{s} \mathrm{l}}^{2}\right)\end{array}\]
Assuming that the slip velocity vsl is much smaller than the line speed vls, this gives:
\[\ \mathrm{m}_{\mathrm{p}}=\rho_{\mathrm{s}} \cdot \frac{\pi}{\mathrm{6}} \cdot \mathrm{d}^{\mathrm{3}} \quad\text{ giving: }\quad \Delta \mathrm{E}_{\mathrm{s}, \mathrm{k i n}, \mathrm{p}}=\frac{\mathrm{1}}{\mathrm{2}} \cdot \mathrm{m}_{\mathrm{p}} \cdot \mathrm{2} \cdot \mathrm{v}_{\mathrm{l} \mathrm{s}} \cdot \mathrm{v}_{\mathrm{s l}}=\mathrm{m}_{\mathrm{p}} \cdot \mathrm{v}_{\mathrm{l s}} \cdot \mathrm{v}_{\mathrm{s l}}=\rho_{\mathrm{s}} \cdot \frac{\pi}{\mathrm{6}} \cdot \mathrm{d}^{\mathrm{3}} \cdot \mathrm{v}_{\mathrm{l s}} \cdot \mathrm{v}_{\mathrm{s} \mathrm{l}}\]
The number of particles in a pipeline with length ΔL and cross-section of the pipe Ap is:
\[\ \mathrm{n=\frac{A_{p} \cdot \Delta L \cdot C_{v s}}{\frac{\pi}{6} \cdot d^{3}}}\]
Giving for the total loss of kinetic energy in a pipe with length ΔL and cross-section of the pipe Ap :
\[\ \Delta \mathrm{E}_{\mathrm{s}, \mathrm{k i n}, \mathrm{t o t}}=\mathrm{n} \cdot \Delta \mathrm{E}_{\mathrm{s}, \mathrm{k i n}, \mathrm{p}}=\mathrm{A}_{\mathrm{p}} \cdot \Delta \mathrm{L} \cdot \mathrm{C}_{\mathrm{v s}} \cdot \mathrm{\rho}_{\mathrm{s}} \cdot \mathrm{v}_{\mathrm{l} \mathrm{s}} \cdot \mathrm{v}_{\mathrm{sl}}\]
The order of magnitude of the time required to dissipate this energy can be determined assuming that this energy also follows from the drag force on a particle:
\[\ \mathrm{F}_{\mathrm{D}}=\mathrm{C}_{\mathrm{D}} \cdot \frac{\mathrm{1}}{2} \cdot \rho_{\mathrm{l}} \cdot \mathrm{v}_{\mathrm{s} \mathrm{l}}^{\mathrm{2}} \cdot \mathrm{A}_{\mathrm{s}}\]
The total drag force on n particles is now:
\[\ \mathrm{F}_{\mathrm{D}, \mathrm{tot}}=\mathrm{n} \cdot \mathrm{C}_{\mathrm{D}} \cdot \frac{1}{2} \cdot \rho_{\mathrm{l}} \cdot \mathrm{v}_{\mathrm{sl}}^{2} \cdot \mathrm{A}_{\mathrm{s}}=\frac{3 \cdot \mathrm{A}_{\mathrm{p}} \cdot \Delta \mathrm{L} \cdot \mathrm{C}_{\mathrm{vs}} \cdot \mathrm{C}_{\mathrm{D}} \cdot \rho_{\mathrm{l}} \cdot \mathrm{v}_{\mathrm{sl}}^{2}}{4 \cdot \mathrm{d}}\]
Since energy or work equals force FD, tot times a distance s, for the distance we find:
\[\ \mathrm{s}=\frac{\Delta \mathrm{E}_{\mathrm{s}, \mathrm{k i n}, \mathrm{t o t}}}{\mathrm{F}_{\mathrm{D}, \mathrm{t o t}}}=\frac{\mathrm{4} \cdot \rho_{\mathrm{s}} \cdot \mathrm{v}_{\mathrm{l s}} \cdot \mathrm{d}}{\mathrm{3} \cdot \rho_{\mathrm{l}} \cdot \mathrm{v}_{\mathrm{s} \mathrm{l}} \cdot \mathrm{C}_{\mathrm{D}}}\]
The time required to travel the distance s equals the distance s divided by the line speed vls, thus:
\[\ \mathrm{\Delta t=\frac{4 \cdot \rho_{s} \cdot d}{3 \cdot \rho_{l} \cdot v_{s l} \cdot C_{D}}}\]
In the Stokes region this can be written as the relaxation time used in the Stokes number:
\[\ \mathrm{\Delta t}=\frac{\mathrm{4 \cdot \rho_{s} \cdot d}}{\mathrm{3 \cdot \rho_{l} \cdot v_{s l} \cdot C_{D}}}=\frac{\mathrm{4 \cdot \rho_{s} \cdot d \cdot R e_{p}}}{\mathrm{3 \cdot \rho_{l} \cdot v_{s l} \cdot 24}}=\frac{\mathrm{4 \cdot \rho_{s} \cdot d \cdot v_{s l} \cdot d}}{\mathrm{3 \cdot \rho_{l} \cdot v_{s l}} \cdot 24 \cdot v}=\frac{\mathrm{d^{2} \cdot \rho_{s}}}{\mathrm{18 \cdot \rho_{l}} \cdot v}\]
The power required for constantly adding the dissipated kinetic energy to the mixture equals the energy losses divided by the time in which they take place, thus:
\[\ \Delta \mathrm{P}_{\mathrm{s}, \mathrm{k i n}}=\frac{\Delta \mathrm{E}_{\mathrm{s}, \mathrm{k i n}, \mathrm{t o t}}}{\Delta \mathrm{t}}=\frac{\mathrm{3} \cdot \mathrm{A}_{\mathrm{p}} \cdot \Delta \mathrm{L} \cdot \mathrm{C}_{\mathrm{v s}} \cdot \mathrm{\rho}_{\mathrm{l}} \cdot \mathrm{v}_{\mathrm{l} \mathrm{s}} \cdot \mathrm{v}_{\mathrm{s} \mathrm{l}}^{2} \cdot \mathrm{C}_{\mathrm{D}}}{\mathrm{4} \cdot \mathrm{d}}\]
This gives the hydraulic gradient required for the compensation of the losses of kinetic energy of:
\[\ \frac{\Delta \mathrm{p}_{\mathrm{s}, \mathrm{k i n}}}{\Delta \mathrm{L}}=\frac{\Delta \mathrm{P}_{\mathrm{s}, \mathrm{k i n}}}{\mathrm{A}_{\mathrm{p}} \cdot \Delta \mathrm{L} \cdot \mathrm{v}_{\mathrm{l} \mathrm{s}}}=\frac{\mathrm{3} \cdot \rho_{\mathrm{l}} \cdot \mathrm{v}_{\mathrm{s} \mathrm{l}}^{\mathrm{2}} \cdot \mathrm{C}_{\mathrm{D}}}{\mathrm{4} \cdot \mathrm{d}} \cdot \mathrm{C}_{\mathrm{v} \mathrm{s}}\]
In the Stokes region the drag coefficient CD is:
\[\ \mathrm{C_{D}}=\frac{24}{\mathrm{R e_{p}}}=\frac{24 \cdot v_{\mathrm{l}}}{\mathrm{v_{s l} \cdot d}}\]
For the laminar Stokes region the hydraulic gradient can now be written as:
\[\ \frac{\Delta \mathrm{p}_{\mathrm{s}, \mathrm{k i n}}}{\Delta \mathrm{L}}=\frac{\Delta \mathrm{P}_{\mathrm{s}, \mathrm{k i n}}}{\mathrm{A}_{\mathrm{p}} \cdot \Delta \mathrm{L} \cdot \mathrm{v}_{\mathrm{l s}}}=\mathrm{1 8} \cdot \frac{\rho_{\mathrm{l}} \cdot \mathrm{v}_{\mathrm{s} \mathrm{l}} \cdot v_{\mathrm{l}}}{\mathrm{d}^{2}} \cdot \mathrm{C}_{\mathrm{v s}}\]
In the turbulent region the drag coefficient CD is:
\[\ \begin{array}{left}\mathrm{C}_{\mathrm{D}}=\mathrm{0 . 4 4 5} &\text{for spheres}\\
\mathrm{C}_{\mathrm{D}} \approx \mathrm{1} &\text{for sand}\end{array}\]
For the turbulent region the hydraulic gradient can now be written as:
\[\ \begin{array}{left} \frac{\Delta \mathrm{p}_{\mathrm{s}, \text {kin}}}{\Delta \mathrm{L}}=\mathrm{0 . 3 3} \cdot \frac{\rho_{\mathrm{l}} \cdot \mathrm{v}_{\mathrm{sl}}^{2}}{\mathrm{d}} \cdot \mathrm{C}_{\mathrm{v s}} \quad\text{ for spheres}\\
\frac{\Delta \mathrm{p}_{\mathrm{s}, \mathrm{k i n}}}{\Delta \mathrm{L}}=\mathrm{0 . 7 5} \cdot \frac{\rho_{\mathrm{l}} \cdot \mathrm{v}_{\mathrm{sl}}^{2}}{\mathrm{d}} \cdot \mathrm{C}_{\mathrm{v s}} \quad\text{ for sand particles}\end{array}\]
Using the equation for the drag coefficient to replace the drag coefficient in equation (7.5-30) with the terminal settling velocity, gives:
\[\ \mathrm{C_{D}=\frac{4 \cdot g \cdot\left(\rho_{s}-\rho_{\mathrm{l}}\right) \cdot d}{3 \cdot \rho_{l} \cdot v_{t}^{2}}=\frac{4 \cdot g \cdot R_{s d} \cdot d}{3 \cdot v_{t}^{2}}}\]
This gives for the pressure losses due to kinetic energy:
\[\ \frac{\Delta \mathrm{p}_{\mathrm{s}, \mathrm{k i n}}}{\Delta \mathrm{L}}=\rho_{\mathrm{l}} \cdot\left(\frac{\mathrm{v}_{\mathrm{s} \mathrm{l}}}{\mathrm{v}_{\mathrm{t}}}\right)^{2} \cdot \mathrm{g} \cdot \mathrm{R}_{\mathrm{s d}} \cdot \mathrm{C}_{\mathrm{v s}}\]
In terms of the hydraulic gradient this gives:
\[\ \mathrm{i}_{\mathrm{s}, \mathrm{k i n}}=\frac{\Delta \mathrm{p}_{\mathrm{s}, \mathrm{k i n}}}{\rho_{\mathrm{l}} \cdot \mathrm{g} \cdot \Delta \mathrm{L}}=\left(\frac{\mathrm{v}_{\mathrm{s l}}}{\mathrm{v}_{\mathrm{t}}}\right)^{2} \cdot \mathrm{R}_{\mathrm{s d}} \cdot \mathrm{C}_{\mathrm{v} \mathrm{s}}\]
In terms of the relative excess hydraulic gradient component Erhg due to kinetic energy losses Srs this gives the ratio of the slip velocity to the terminal settling velocity squared:
| \[\ \mathrm{S}_{\mathrm{r s}}=\frac{\mathrm{i}_{\mathrm{s}, \mathrm{k i n}}}{\mathrm{R}_{\mathrm{s d}} \cdot \mathrm{C}_{\mathrm{v s}}}=\left(\frac{\mathrm{v}_{\mathrm{s l}}}{\mathrm{v}_{\mathrm{t}}}\right)^{\mathrm{2}}\] |
Viscous + Potential + Kinetic Energy
The total pressure required to push the solids/liquid mixture through the pipeline is now:
\[\ \Delta \mathrm{p}_{\mathrm{m}}=\Delta \mathrm{p}_{\mathrm{l}}+\Delta \mathrm{p}_{\mathrm{s}, \mathrm{p} \mathrm{o t}}+\Delta \mathrm{p}_{\mathrm{s}, \mathrm{k i n}}=\Delta \mathrm{p}_{\mathrm{l}} \cdot\left(\mathrm{1}+\frac{\Delta \mathrm{p}_{\mathrm{s}, \mathrm{p} \mathrm{o t}}}{\Delta \mathrm{p}_{\mathrm{l}}}+\frac{\Delta \mathrm{p}_{\mathrm{s,kin}}}{\Delta \mathrm{p}_{\mathrm{l}}}\right)\]
Substituting equations (7.5-7) for the potential energy losses and (7.5-36) for the kinetic energy losses gives:
\[\ \begin{array}{left} \mathrm{\Delta p_m=\Delta p_l \cdot \left(1+\frac{\rho_l \cdot \left(\frac{v_t \cdot \left(\ 1-\frac{C_{vs}}{\kappa_C} \right)}{v_{ls}}^{\beta} \right)\cdot g \cdot R_{sd}\cdot C_{vs}}{\lambda_l \cdot \frac{1}{D_p}\cdot \frac{1}{2}\cdot \rho_l\cdot v_{ls}^2}+ \frac{\rho_l\cdot \left( \frac{v_{sl}}{v_t} \right)^2 \cdot g\cdot R_{sd}\cdot C_{vs}}{\lambda_l \cdot \frac{1}{D_p}\cdot \frac{1}{2} \cdot \rho_l \cdot v_{ls}^2} \right)}\\
\mathrm{\Delta p_m=\Delta p_l \cdot \left(1+\frac{(2 \cdot g\cdot R_{sd}\cdot D_p)}{\lambda_l}\cdot C_{vs}\cdot \frac{1}{v_{ls}^2}\cdot \left(\frac{v_t \cdot \left( 1-\frac{C_{vs}}{\kappa_C} \right)^{\beta}}{v_{ls}} +\left(\frac{v_{sl}}{v_t} \right)^2 \right) \right)}
\end{array}\]
In terms of the hydraulic gradient im this gives:
\[\ \mathrm{i}_{\mathrm{m}}=\mathrm{i}_{\mathrm{l}} \cdot\left(1+\frac{\left(2 \cdot \mathrm{g} \cdot \mathrm{R}_{\mathrm{sd}} \cdot \mathrm{D}_{\mathrm{p}}\right)}{\lambda_{\mathrm{l}}} \cdot \mathrm{C}_{\mathrm{v s}} \cdot \frac{\mathrm{1}}{\mathrm{v}_{\mathrm{l s}}^{2}} \cdot\left(\frac{\mathrm{v}_{\mathrm{t}} \cdot\left(\mathrm{1}-\frac{\mathrm{C}_{\mathrm{v s}}}{\mathrm{\kappa}_{\mathrm{C}}}\right)^{\beta}}{\mathrm{v}_{\mathrm{l s}}}+\left(\frac{\mathrm{v}_{\mathrm{sl}}}{\mathrm{v}_{\mathrm{t}}}\right)^{2}\right)\right)\]
In terms of the relative excess hydraulic gradient Erhg this gives:
\[\ \mathrm{E}_{\mathrm{rhg}}=\frac{\mathrm{i}_{\mathrm{m}}-\mathrm{i}_{\mathrm{l}}}{\mathrm{R}_{\mathrm{sd}} \cdot \mathrm{C}_{\mathrm{vs}}}=\frac{\mathrm{v}_{\mathrm{t}} \cdot\left(1-\frac{\mathrm{C}_{\mathrm{vs}}}{\mathrm{\kappa}_{\mathrm{C}}}\right)^{\beta}}{\mathrm{v}_{\mathrm{ls}}}+\left(\frac{\mathrm{v}_{\mathrm{sl}}}{\mathrm{v}_{\mathrm{t}}}\right)^{2}=\mathrm{S}_{\mathrm{hr}}+\mathrm{S}_{\mathrm{rs}}\]
Note that the term for potential energy losses contains the hindered settling influence, while the kinetic energy term does not, because the drag coefficient is replaced by the terminal settling velocity without hindered settling. The first term is similar to the Newitt et al. (1955) equation (1955), but with a different coefficient. Newitt et al. (1955) uses a factor of 1100, which should be the result of 2/λl. However, applying a λl=0.02 for smooth pipes and high Reynolds numbers results in a factor of 100. Newitt et al. (1955) however did not include the kinetic energy term as such. Equation (7.5-21) shows that the loss of kinetic energy is proportional to the line speed vls and the slip velocity vsl. The question is, is the slip velocity vsl a constant or does it depend on parameters like the line speed vls, the terminal settling velocity vt and the concentration Cvs.
7.5.3 Estimating the Slip Velocity
In order to get some impression regarding the slip velocity, first consider that the kinetic energy losses depend on collisions between particles and the pipe wall. According to equation (7.5-21) the slip velocity can be expressed as:
\[\ \Delta \mathrm{E}_{\mathrm{s}, \mathrm{k i n}, \mathrm{p}}=\mathrm{m}_{\mathrm{p}} \cdot \mathrm{v}_{\mathrm{l} \mathrm{s}} \cdot \mathrm{v}_{\mathrm{sl}} \quad \Rightarrow \quad\mathrm{v}_{\mathrm{s l}}=\frac{\Delta \mathrm{E}_{\mathrm{s}, \mathrm{k i n}, \mathrm{p}}}{\mathrm{m}_{\mathrm{p}} \cdot \mathrm{v}_{\mathrm{ls}}}\]
Which is roughly the energy loss per collision or interaction, divided by the momentum of the particle.
Small Particles:
Now suppose the energy loss per collision or interaction equals the kinetic energy of a particle, based on a factor αk times the terminal settling velocity vt:
\[\ \Delta \mathrm{E}_{\mathrm{s}, \mathrm{k i n}, \mathrm{p}}=\frac{\mathrm{1}}{2} \cdot \mathrm{m}_{\mathrm{p}} \cdot\left(\alpha_{\mathrm{k}} \cdot \mathrm{v}_{\mathrm{t}}\right)^{2} \quad \Rightarrow \quad\mathrm{v}_{\mathrm{s l}}=\frac{\frac{\mathrm{1}}{\mathrm{2}} \cdot \mathrm{m _ { p }} \cdot\left(\alpha_{\mathrm{k}} \cdot \mathrm{v}_{\mathrm{t}}\right)^{2}}{\mathrm{m}_{\mathrm{p}} \cdot \mathrm{v}_{\mathrm{l} \mathrm{s}}}=\frac{\alpha_{\mathrm{k}}^{2}}{2} \cdot \frac{\mathrm{v}_{\mathrm{t}}^{2}}{\mathrm{v}_{\mathrm{ls}}}\]
The contribution of the kinetic energy losses to the relative excess hydraulic gradient Erhg, the Srs parameter is now:
\[\ \mathrm{S}_{\mathrm{r s}}=\left(\frac{\mathrm{v}_{\mathrm{s} \mathrm{l}}}{\mathrm{v}_{\mathrm{t}}}\right)^{2}=\left(\frac{\alpha_{\mathrm{k}}^{\mathrm{2}}}{\mathrm{2}} \cdot \frac{\mathrm{v}_{\mathrm{t}}}{\mathrm{v}_{\mathrm{l} \mathrm{s}}}\right)^{2}=\frac{\alpha_{\mathrm{k}}^{4}}{4} \cdot \frac{\mathrm{v}_{\mathrm{t}}^{2}}{\mathrm{v}_{\mathrm{l} \mathrm{s}}^{2}}\]
Large Particles:
Another assumption may be that the translational kinetic energy loss per interaction is proportional to the momentum of a particle based on the terminal setting velocity vt with a factor αm.
\[\ \Delta \mathrm{E}_{\mathrm{s}, \mathrm{k i n}, \mathrm{p}}=\mathrm{m}_{\mathrm{p}} \cdot\left(\alpha_{\mathrm{m}} \cdot \mathrm{v}_{\mathrm{t}}\right)\quad \Rightarrow \quad\mathrm{v}_{\mathrm{s} \mathrm{l}}=\frac{\alpha_{\mathrm{m}} \cdot \mathrm{m}_{\mathrm{p}} \cdot \mathrm{v}_{\mathrm{t}}}{\mathrm{m}_{\mathrm{p}} \cdot \mathrm{v}_{\mathrm{l} \mathrm{s}}}=\alpha_{\mathrm{m}} \cdot \frac{\mathrm{v}_{\mathrm{t}}}{\mathrm{v}_{\mathrm{l s}}}\]
The contribution of the kinetic energy losses to the relative excess hydraulic gradient Erhg, the Srs parameter is now:
\[\ \mathrm{S}_{\mathrm{r s}}=\left(\frac{\mathrm{v}_{\mathrm{s} \mathrm{l}}}{\mathrm{v}_{\mathrm{t}}}\right)^{2}=\left(\alpha_{\mathrm{m}} \cdot \frac{\mathrm{1}}{\mathrm{v}_{\mathrm{l s}}}\right)^{2}=\alpha_{\mathrm{m}}^{2} \cdot \frac{\mathrm{1}}{\mathrm{v}_{\mathrm{l} \mathrm{s}}^{2}}\]
Medium Particles:
The transition between the above two assumptions could be that the translational kinetic energy loss per interaction is proportional to the terminal settling velocity to a power of 1.5, based on the terminal setting velocity vt with a factor αt.
\[\ \Delta \mathrm{E}_{\mathrm{s}, \mathrm{k i n}, \mathrm{p}}=\mathrm{m}_{\mathrm{p}} \cdot\left(\alpha_{\mathrm{t}} \cdot \mathrm{v}_{\mathrm{t}}\right)^{\mathrm{3} / 2}\quad \Rightarrow\quad \mathrm{v}_{\mathrm{s l}}=\frac{\alpha_{\mathrm{t}}^{\mathrm{3} / \mathrm{2}} \cdot \mathrm{m}_{\mathrm{p}} \cdot \mathrm{v}_{\mathrm{t}}^{\mathrm{3} / 2}}{\mathrm{m}_{\mathrm{p}} \cdot \mathrm{v}_{\mathrm{l} \mathrm{s}}}=\alpha_{\mathrm{t}}^{\mathrm{3} / 2} \cdot \frac{\mathrm{v}_{\mathrm{t}}^{\mathrm{3} / 2}}{\mathrm{v}_{\mathrm{l} \mathrm{s}}}\]
The contribution of the kinetic energy losses to the relative excess hydraulic gradient Erhg, the Srs parameter is now:
\[\ \mathrm{S}_{\mathrm{r s}}=\left(\frac{\mathrm{v}_{\mathrm{s} \mathrm{l}}}{\mathrm{v}_{\mathrm{t}}}\right)^{2}=\left(\alpha_{\mathrm{t}}^{\mathrm{3} / 2} \cdot \frac{\mathrm{v}_{\mathrm{t}}^{1 / 2}}{\mathrm{v}_{\mathrm{l} \mathrm{s}}}\right)^{2}=\alpha_{\mathrm{t}}^{3} \cdot \frac{\mathrm{v}_{\mathrm{t}}}{\mathrm{v}_{\mathrm{ls}}^{\mathrm{2}}}\]
Although these are reasonable first assumptions, the loss of kinetic energy will most probably depend on more factors. Assuming that the loss of translational kinetic energy is mainly caused by the transition of translational kinetic energy to rotational kinetic energy, whether this is the result of interactions with the viscous sub-layer velocity gradient or by collision to the pipe wall. The rotation of the particles results in a radial inwards lift force (for example the near wall lift force) due to the velocity gradient, especially in the viscous sub-layer and due to the magnitude of the slip velocity. This radial inwards lift force will first decelerate the particle outward radial velocity and then accelerate particles giving them an inward radial velocity. It seems like particles having an outward radial velocity, will bounce back on the viscous sub-layer or for large particles partly on the viscous sub- layer and partly on the pipe wall. Since the velocity gradient in the viscous sub-layer, but also in the buffer layer, increases with the line speed and the inwards radial lift force depends on this velocity gradient, the time and thus the penetration distance required to make a particle bounce back on the viscous sub-layer will be reversely proportional to the line speed. So the increase of the velocity gradient in the viscous sub-layer with the line speed on one hand and the time required to develop enough lift force to make the particle bounce back being reversely proportional to the line speed, neutralize each other. Maybe not completely, but the result will be that the loss of kinetic translational energy, being the gained rotational kinetic energy, will be almost independent of the line speed. Since a slurry in general does not consist of spherical particles, will not be uniform in general and will have a lot of interactions between the particles, a real slurry may deviate from this assumption, resulting in at least a different proportionality constant as is discussed later. Still the starting point will be that the loss of translational kinetic energy is independent of the line speed. Non-spherical particles will have a larger drag coefficient and will be more sensitive for loosing translational energy, resulting in higher losses. The gained rotational energy will be dissipated in the turbulent flow.
A first parameter is the ratio of the thickness of the viscous sub-layer to the particle diameter, since the interaction or collision with the pipe wall will take place in the viscous sub-layer. Due to the interaction or collision, the particle will start rotating and part of the translational kinetic energy will be transferred into rotational kinetic energy, which will be transferred into heat by viscous friction later. This ratio is an indication of the concentration of particles in the viscous sub layer, due to geometry, and is a measure for the lubrication in the viscous sub layer. This ratio can never be larger than 1 (only for very small particles and/or very low line speeds), meaning the concentration in the viscous sub layer equals the average concentration. The ratio of the thickness of the viscous sub-layer to the particle diameter is:
\[\ \frac{\delta_{\mathrm{v}}}{\mathrm{d}}=\frac{\mathrm{1 1 . 6} \cdot \frac{v_{\mathrm{l}}}{\mathrm{u}_{*}}}{\mathrm{d}}=\frac{\mathrm{1 1 . 6} \cdot v_{\mathrm{l}}}{\sqrt{\lambda_{\mathrm{l}} / \mathrm{8}} \cdot \mathrm{v}_{\mathrm{ls}} \cdot \mathrm{d}}=\frac{\mathrm{3 2 . 8 1}{ \cdot v _ { \mathrm{l} }}}{\sqrt{\lambda_{\mathrm{l}}} \cdot \mathrm{v}_{\mathrm{l s}} \cdot \mathrm{d}}\]
A second parameter is the ratio between the terminal settling velocity and the maximum velocity in the viscous sub-layer, giving an indication of the angle under which the particle will hit the viscous sub-layer, the angle of attack or the collision impact factor (Figure 7.5-1):
\[\ \text{angle of attack } =\left(\frac{\mathrm{v}_{\mathrm{t}}}{\mathrm{1 1 . 6} \cdot \mathrm{u}_{*}}\right)=\left(\frac{\mathrm{v}_{\mathrm{t}}}{1 \mathrm{1 . 6} \cdot \sqrt{\frac{\lambda_{\mathrm{l}}}{\mathrm{8}}}{ \cdot \mathrm{v}_{\mathrm{l s}}}}\right)=\left(\frac{\mathrm{v}_{\mathrm{t}}}{4.1 \cdot \sqrt{\lambda_{\mathrm{l}}} \cdot \mathrm{v}_{\mathrm{l s}}}\right)\]
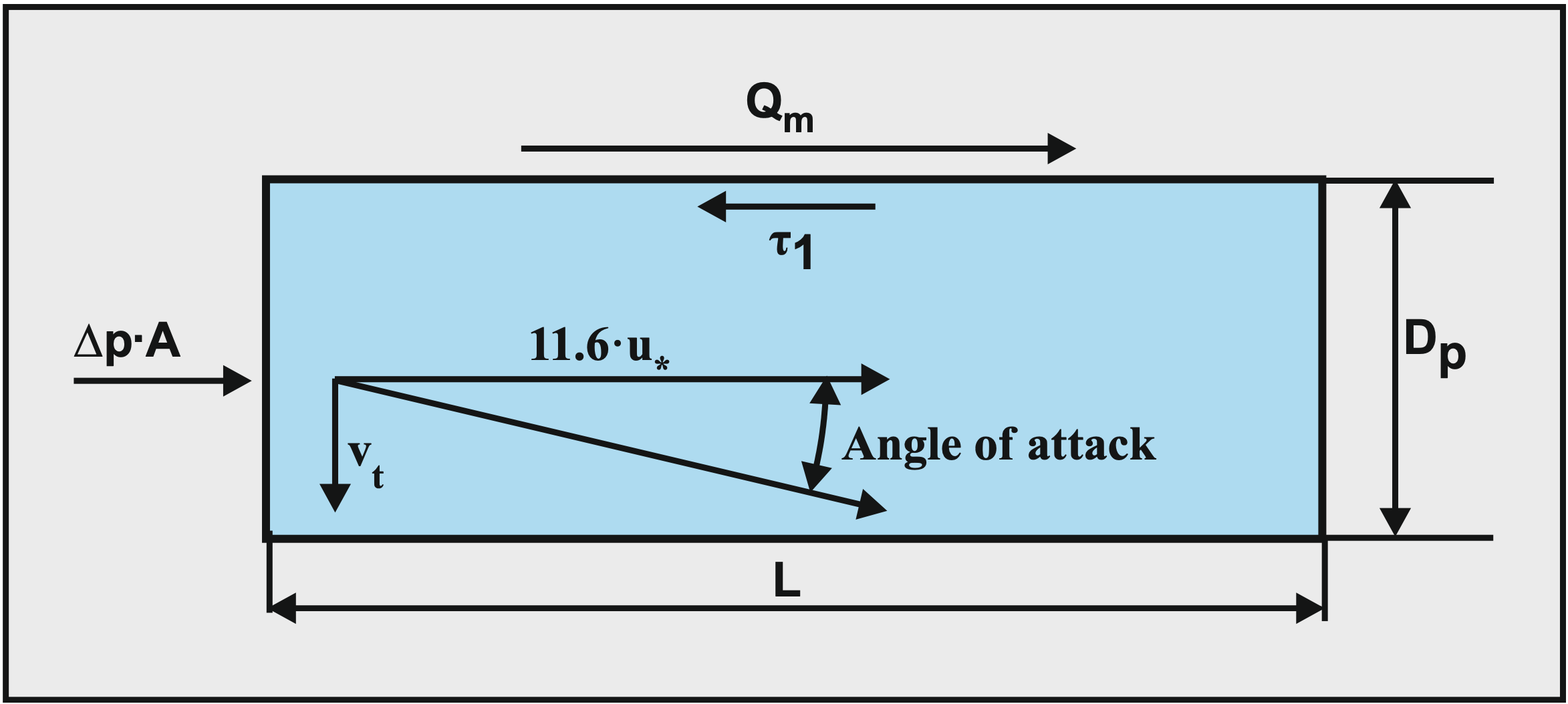
A third parameter is the drag coefficient CD. Different drag coefficients are involved. On one hand the translational drag coefficient, used to determine the translational drag force. On the other hand the rotational drag force used to determine the rotational acceleration of a particle in a flow with rotation. In its current form, the coefficient as used here describes the drag coefficient of the particle.
A fourth parameter is the relative submerged density Rsd.
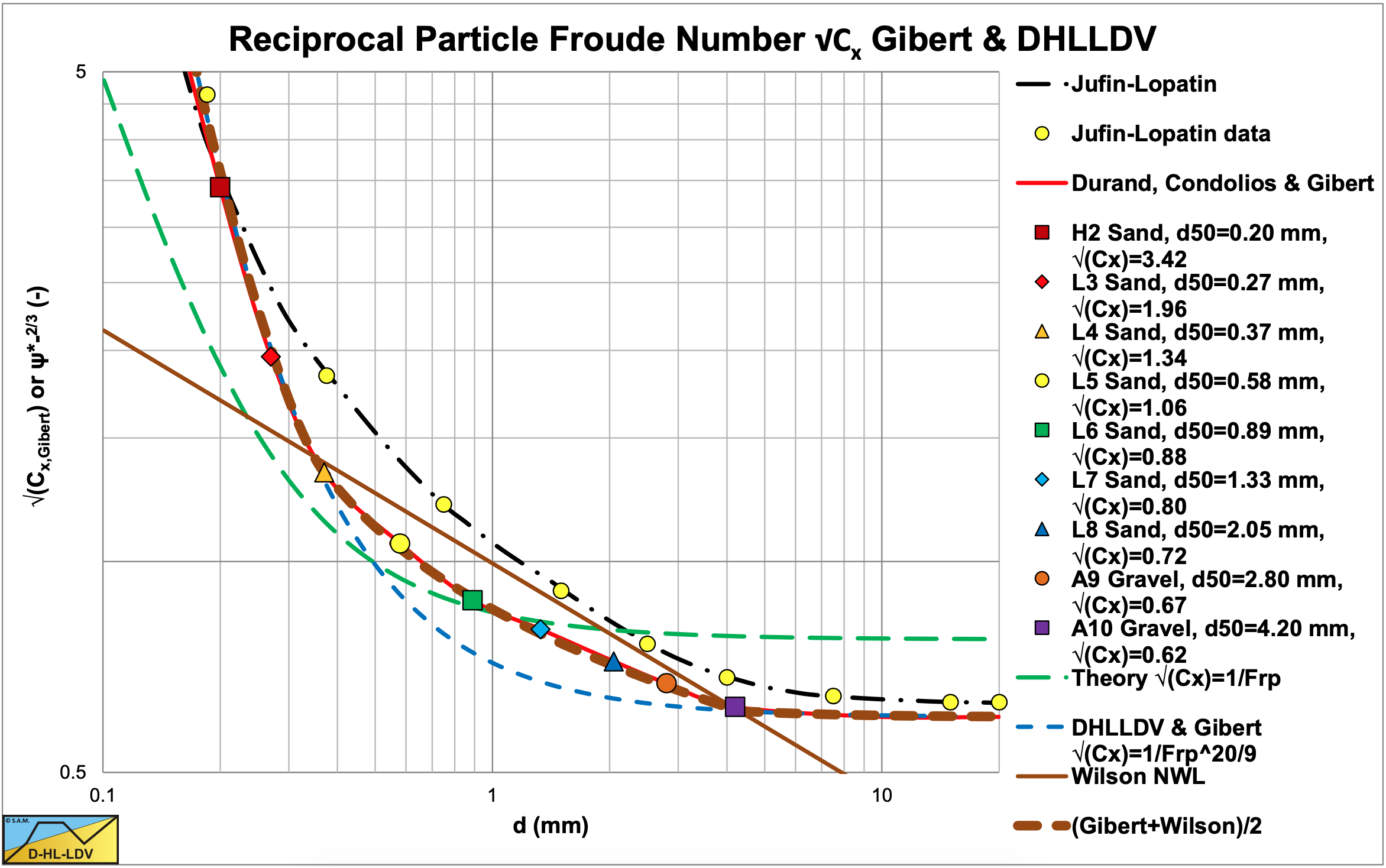
Since Durand & Condolios (1952) already determined the influence of the particle Froude number on the head losses, this particle Froude number will be used as a measure for the drag coefficients, so resulting equations can be compared.
\[\ \mathrm{F r}_{\mathrm{p}}=\left(\frac{\mathrm{v}_{\mathrm{t}}}{\sqrt{\mathrm{g} \cdot \mathrm{d}}}\right)=\left(\frac{4}{3} \cdot \frac{\xi \cdot \mathrm{R}_{\mathrm{s d}}}{\mathrm{C}_{\mathrm{D}}}\right)^{1 / 2} \approx\left(\frac{\mathrm{R}_{\mathrm{s d}}}{\mathrm{C}_{\mathrm{D}}}\right)^{1 / 2}\]
The Froude number on the right side is a modified Froude number, calibrated on experiments and the use of the Zanke settling velocity equation. Last but not least, the terminal settling velocity is chosen as a fifth parameter. This gives for the translational kinetic energy loss per interaction or collision:
\[\ \Delta \mathrm{E}_{\mathrm{s}, \mathrm{k i n}, \mathrm{p}}=\mathrm{m}_{\mathrm{p}} \cdot \mathrm{v}_{\mathrm{s l}} \cdot \mathrm{v}_{\mathrm{l s}}=\mathrm{c} \cdot \mathrm{m}_{\mathrm{p}} \cdot\left(\frac{\delta_{\mathrm{v}}}{\mathrm{d}}\right)^{\alpha_{1}} \cdot\left(\frac{\mathrm{v}_{\mathrm{t}}}{\mathrm{1 1 .6} \cdot \mathrm{u}_{*}}\right)^{\alpha_{2}} \cdot\left(\left(\frac{\mathrm{R}_{\mathrm{s d}}}{\mathrm{C}_{\mathrm{D}}}\right)^{1 / 2}\right)^{\alpha_{3}} \cdot \mathrm{v}_{\mathrm{t}} \cdot \mathrm{v}_{\mathrm{l} \mathrm{s}}\]
This can also be written as:
\[\ \Delta \mathrm{E}_{\mathrm{s}, \mathrm{k i n}, \mathrm{p}}=\mathrm{m}_{\mathrm{p}} \cdot \mathrm{v}_{\mathrm{s l}} \cdot \mathrm{v}_{\mathrm{l s}}=\mathrm{c \cdot m _ { p }} \cdot\left(\frac{\mathrm{3 2 .8 1 \cdot }{v _ { \mathrm{l} }}}{\sqrt{\lambda_{\mathrm{l}}} \cdot \mathrm{v}_{\mathrm{l s}} \cdot \mathrm{d}}\right)^{\alpha_{1}} \cdot\left(\frac{\mathrm{v}_{\mathrm{t}}}{\mathrm{4 .1 \cdot} \sqrt{\lambda_{\mathrm{l}}} \cdot \mathrm{v}_{\mathrm{l s}}}\right)^{\alpha_{2}} \cdot\left(\left(\frac{\mathrm{R}_{\mathrm{s d}}}{\mathrm{C}_{\mathrm{D}}}\right)^{\mathrm{1 / 2}}\right)^{\alpha_{3}} \cdot \mathrm{v}_{\mathrm{t}} \cdot \mathrm{v}_{\mathrm{l s}}\]
Because of the assumption that the loss of translational kinetic energy per interaction is independent of the line speed, the following condition is valid:
\[\ \alpha_{1}+\alpha_{2}=1\]
Equation (7.5-54) can also be written as, matching the Durand & Condolios (1952) particle Froude number:
\[\ \Delta \mathrm{E}_{\mathrm{s}, \mathrm{k i n}, \mathrm{p}}=\mathrm{c} \cdot \mathrm{m}_{\mathrm{p}} \cdot\left(\frac{\mathrm{3 2 .8 1}}{\sqrt{\lambda_{\mathrm{l}}}}\right)^{\alpha_{1}} \cdot\left(\frac{\mathrm{1}}{\mathrm{4 .1} \cdot \sqrt{\lambda_{\mathrm{l}}}}\right)^{\alpha_{2}} \cdot \frac{\mathrm{v}_{\mathrm{t}}^{\mathrm{\alpha}_{\mathrm{2}}+\alpha_{\mathrm{3}}}}{\sqrt{\mathrm{g} \cdot \mathrm{d}}^{ 2 \cdot \mathrm{\alpha}_{1}+\alpha_{3}}} \cdot \frac{\left(v_{\mathrm{l}} \cdot \mathrm{g}\right)^{\alpha_{1}}}{\mathrm{v}_{\mathrm{l} \mathrm{s}}^{\alpha_{1}+\alpha_{2}}} \cdot \mathrm{v}_{\mathrm{t}} \cdot \mathrm{v}_{\mathrm{l} \mathrm{s}}\]
Assuming the terms in this equation are dimensionless as well, the following relations are found:
\[\ \alpha_{2}+\alpha_{3}=2 \cdot \alpha_{1}+\alpha_{3}\quad \Rightarrow \quad\alpha_{2}=2 \cdot \alpha_{1} \quad\text{ and }\quad \alpha_{1}+\alpha_{2}=3 \cdot \alpha_{1} \quad\Rightarrow \quad\alpha_{2}=2 \cdot \alpha_{1}\]
This gives α1=1/3 and α2=2/3. In order to find a value for α3, the data of Gibert (1960) are used. According to Miedema (2013) the total power of the particle Froude number in the Durand & Condolios (1952) equation should not be 1.5, but about 10/3, which is α2+α3 squared. This gives: α2+α3=10/6=5/3. Since α2=2/3, this gives α3=1:
\[\ \Delta \mathrm{E}_{\mathrm{s}, \mathrm{k i n}, \mathrm{p}}=\mathrm{c} \cdot \mathrm{m}_{\mathrm{p}} \cdot\left(\frac{\delta_{\mathrm{v}}}{\mathrm{d}}\right)^{2 / 6} \cdot\left(\frac{\mathrm{v}_{\mathrm{t}}}{\mathrm{1 1 .6} \cdot \mathrm{u}_{*}}\right)^{4 / \mathrm{6}} \cdot\left(\frac{\mathrm{v}_{\mathrm{t}}}{\sqrt{\mathrm{g} \cdot \mathrm{d}}}\right)^{\mathrm{1}} \cdot \mathrm{v}_{\mathrm{t}} \cdot \mathrm{v}_{\mathrm{ls}}\]
Or
\[\ \Delta \mathrm{E}_{\mathrm{s}, \mathrm{kin}, \mathrm{p}}=1.25 \cdot \mathrm{c} \cdot \mathrm{m}_{\mathrm{p}} \cdot\left(\frac{1}{\sqrt{\lambda_{\mathrm{l}}}}\right) \cdot\left(\frac{\mathrm{v}_{\mathrm{t}}}{\sqrt{\mathrm{g} \cdot \mathrm{d}}}\right)^{5 / 3} \cdot\left(\frac{\left(v_{\mathrm{l}} \cdot \mathrm{g}\right)^{1 / 3}}{\mathrm{v}_{\mathrm{ls}}}\right) \cdot \mathrm{v}_{\mathrm{t}} \cdot \mathrm{v}_{\mathrm{ls}} \quad\text{ with: }\quad\left(\frac{32.81}{4.1^{2}}\right)^{1 / 3}=1.25\]
The above equations give for the slip velocity:
\[\ \mathrm{v}_{\mathrm{s l}}=\frac{\Delta \mathrm{E}_{\mathrm{s}, \mathrm{k i n}, \mathrm{p}}}{\mathrm{m}_{\mathrm{p}} \cdot \mathrm{v}_{\mathrm{l} \mathrm{s}}}=\mathrm{c} \cdot\left(\frac{\delta_{\mathrm{v}}}{\mathrm{d}}\right)^{2 / 6} \cdot\left(\frac{\mathrm{v}_{\mathrm{t}}}{\mathrm{1 1 .6} \cdot \mathrm{u}_{*}}\right)^{4 / 6} \cdot\left(\frac{\mathrm{v}_{\mathrm{t}}}{\sqrt{\mathrm{g} \cdot \mathrm{d}}}\right)^{\mathrm{1}} \cdot \mathrm{v}_{\mathrm{t}}\]
Or, using other dimensionless relations:
\[\ \mathrm{v}_{\mathrm{s l}}=\mathrm{1 .2 5} \cdot \mathrm{c} \cdot\left(\frac{\mathrm{1}}{\sqrt{\lambda_{\mathrm{l}}}}\right) \cdot\left(\frac{\mathrm{v}_{\mathrm{t}}}{\sqrt{\mathrm{g} \cdot \mathrm{d}}}\right)^{5 / 3} \cdot\left(\frac{\left(v_{\mathrm{l}} \cdot \mathrm{g}\right)^{1 / 3}}{\mathrm{v}_{\mathrm{l s}}}\right) \cdot \mathrm{v}_{\mathrm{t}}\]
Also based on Durand & Condolios (1952) and many others, the proportionality coefficient c is determined to be about c=6.8. The powers and the proportionality coefficient match the findings of Miedema & Ramsdell (2013), but with the addition of the friction coefficient λl in the equations and a slightly higher power of the line speed term, 1 instead of 0.89. In the slip velocity notation, Durand & Condolios (1952), Newitt at al. (1955), Fuhrboter (1961) and Jufin & Lopatin (1966) would have a power of 0.5, Zandi & Govatos (1967) a power of 0.93 and Wilson et al. (1992) a maximum power of 0.85. Wilson et al. (1992) state that the highest power has to be applied for uniform sands, while this power decreases depending on the sand. An upper limit of a power of 1, matching the assumption that the energy loss per interaction does not depend on the line speed, seems reasonable. The reason for a lower power for non-uniforms sands and gravels may be found in the way the Erhg curves for the different fractions are added to a curve for the whole PSD. For the full range of particle diameters the contribution of the translational kinetic energy losses, the Srs parameter, is:
\[\ \mathrm{S}_{\mathrm{r} \mathrm{s}}=\left(\frac{\mathrm{v}_{\mathrm{sl}}}{\mathrm{v}_{\mathrm{t}}}\right)^{2}=\mathrm{8 .5}^{2} \cdot\left(\frac{\mathrm{1}}{\lambda_{\mathrm{l}}}\right) \cdot\left(\frac{\mathrm{v}_{\mathrm{t}}}{\sqrt{\mathrm{g} \cdot \mathrm{d}}}\right)^{\mathrm{10} / \mathrm{3}} \cdot\left(\frac{\left(v_{\mathrm{l}} \cdot \mathrm{g}\right)^{1 / 3}}{\mathrm{v}_{\mathrm{l s}}}\right)^{2}=\frac{\mathrm{8 .5}^{2}}{\mathrm{8}} \cdot\left(\frac{\mathrm{v}_{\mathrm{t}}}{\sqrt{\mathrm{g} \cdot \mathrm{d}}}\right)^{\mathrm{10} / \mathrm{3}} \cdot\left(\frac{\left(v_{\mathrm{l}} \cdot \mathrm{g}\right)^{1 / 3}}{\sqrt{\lambda_{\mathrm{l}} / \mathrm{8}} \cdot \mathrm{v}_{\mathrm{l} \mathrm{s}}}\right)^{\mathrm{2}}\]
Giving for the relative excess hydraulic gradient, the Erhg parameter:
| \[\ \mathrm{E}_{\mathrm{rhg}}=\frac{\mathrm{i}_{\mathrm{m}}-\mathrm{i}_{\mathrm{l}}}{\mathrm{R}_{\mathrm{sd}} \cdot \mathrm{C}_{\mathrm{vs}}}=\mathrm{S}_{\mathrm{hr}}+\mathrm{S}_{\mathrm{rs}}=\frac{\mathrm{v}_{\mathrm{t}} \cdot\left(1-\frac{\mathrm{C}_{\mathrm{vs}}}{\mathrm{0 . 1 7 5} \cdot(1+\beta)}\right)^{\beta}}{\mathrm{v}_{\mathrm{ls}}}+\mathrm{8 .5}^{2} \cdot\left(\frac{\mathrm{1}}{\lambda_{\mathrm{l}}}\right) \cdot\left(\frac{\mathrm{v}_{\mathrm{t}}}{\sqrt{\mathrm{g} \cdot \mathrm{d}}}\right)^{10 / 3} \cdot\left(\frac{\left(v_{1} \cdot \mathrm{g}\right)^{1 / 3}}{\mathrm{v}_{\mathrm{ls}}}\right)^{2}\] |
The resulting equation, which is the main finding of this chapter, can be considered to be the sedimentation capability (potential energy losses) plus the collision intensity times the collision impact (kinetic energy losses). The coefficient of 8.5 is a good first estimate, but may vary around 8.5 depending on the character of the sand or gravel. In this study, most experiments match the equation well using the coefficient of 8.5. This equation is the basis of the DHLLDV heterogeneous regime model and is used for both uniform and graded sands and gravels.

7.5.4 Simplified Models
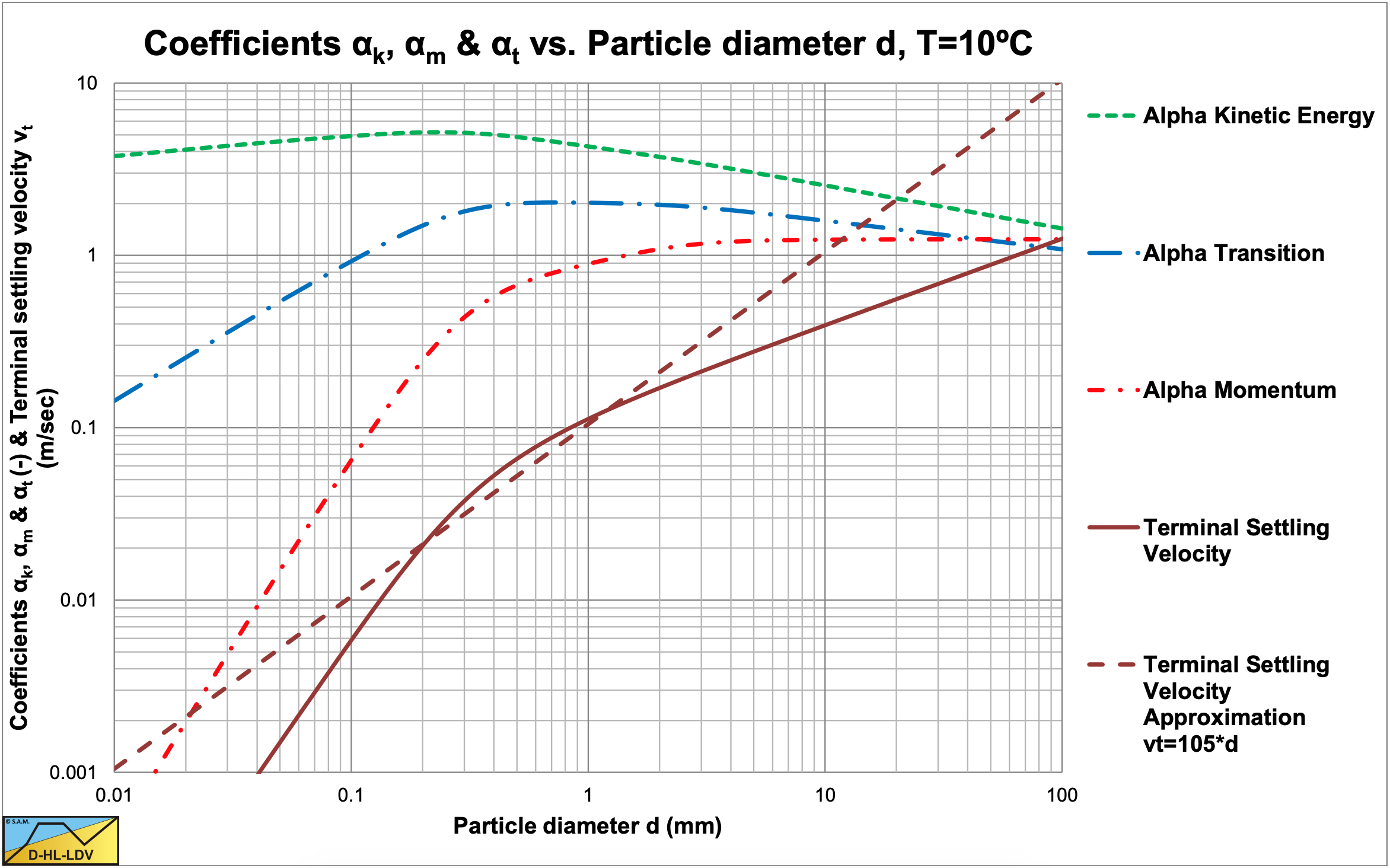
It is now interesting to see if the equation derived can be simplified for 6 specific cases. To do this two kinematic viscosities and three pipe diameters are considered for sand and gravel. The two kinematic viscosities match temperatures of 10oC (reality) and 20oC (laboratory), the pipe diameters are 0.0254 m (small), 0.3 m (medium) and 1.2 m (large). The relative submerged density is assumed to be 1.585 for salt water.
Figure 7.5 2 shows the 3 coefficients as a function of the particle diameter for a Dp=0.3 m pipe and T=10oC, while Table 7.5 1 shows the viscosities and Darcy Weisbach friction factors used here. The simplified models are based on a power of 3 of the particle Froude number instead of 10/3.
|
Viscosity (m2/s) |
Dp=0.0254 m |
Dp=0.3 m |
Dp=1.2 m |
|
|
T=10oC |
0.0000013 |
0.0214 |
0.0113 |
0.0085 |
|
T=20oC |
0.0000010 |
0.0202 |
0.0109 |
0.0082 |
7.5.4.1 Simplified Model for Small Particles, d<0.3 mm
For small particles, d<0.3 mm, in terms of the kinetic translational energy of a particle based on the terminal settling velocity, the following expression can now be found:
\[\ \Delta \mathrm{E}_{\mathrm{s}, \mathrm{k i n}, \mathrm{p}}=\frac{\mathrm{1}}{2} \cdot \mathrm{m}_{\mathrm{p}} \cdot\left(\alpha_{\mathrm{k}} \cdot \mathrm{v}_{\mathrm{t}}\right)^{2}=\mathrm{2} \cdot \mathrm{8 .5} \cdot \frac{\left(v_{\mathrm{l}} \cdot \mathrm{g}\right)^{1 / 3}}{\sqrt{\lambda_{\mathrm{l}}} \cdot \sqrt{\mathrm{g} \cdot \mathrm{d}}} \cdot\left(\frac{\mathrm{v}_{\mathrm{t}}}{\sqrt{\mathrm{g} \cdot \mathrm{d}}}\right)^{1 / 2} \cdot \frac{\mathrm{1}}{2} \cdot \mathrm{m}_{\mathrm{p}} \cdot \mathrm{v}_{\mathrm{t}}^{\mathrm{2}}\]
The factor αk is now:
\[\ \alpha_{k}=\sqrt{2 \cdot 8.5 \cdot \frac{\left(v_{\mathrm{l}} \cdot \mathrm{g}\right)^{1 / 3}}{\sqrt{\lambda_{\mathrm{l}}} \cdot \sqrt{\mathrm{g \cdot d}}} \cdot\left(\frac{\mathrm{v_{t}}}{\sqrt{\mathrm{g \cdot d}}}\right)^{1 / 2}}\]
So for small particles, the slip velocity can be determined as:
\[\ \mathrm{v}_{\mathrm{sl}}=\frac{\Delta \mathrm{E}_{\mathrm{s}, \mathrm{k i n}, \mathrm{p}}}{\mathrm{m}_{\mathrm{p}} \cdot \mathrm{v}_{\mathrm{ls}}}=\frac{\left(\alpha_{\mathrm{k}} \cdot \mathrm{v}_{\mathrm{t}}\right)^{2}}{\mathrm{2} \cdot \mathrm{v}_{\mathrm{l} \mathrm{s}}}\]
This gives for the contribution of the kinetic energy losses to the relative excess hydraulic gradient Erhg, the Srs parameter, for small particles as a first estimate:
\[\ \mathrm{S}_{\mathrm{r s}}=\left(\frac{\mathrm{v}_{\mathrm{s} \mathrm{l}}}{\mathrm{v}_{\mathrm{t}}}\right)^{2}=\left(\frac{\alpha_{\mathrm{k}}^{\mathrm{2}}}{\mathrm{2}} \cdot \frac{\mathrm{v}_{\mathrm{t}}}{\mathrm{v}_{\mathrm{ls}}}\right)^{2}=\beta_{\mathrm{k}} \cdot \frac{\mathrm{v}_{\mathrm{t}}^{2}}{\mathrm{v}_{\mathrm{l s}}^{2}}\]
In terms of the excess hydraulic gradient Erhg this gives:
\[\ \mathrm{E}_{\mathrm{r h g}}=\frac{\mathrm{i}_{\mathrm{m}}-\mathrm{i}_{\mathrm{l}}}{\mathrm{R}_{\mathrm{s d}} \cdot \mathrm{C}_{\mathrm{v s}}}=\mathrm{S}_{\mathrm{h r}}+\mathrm{S}_{\mathrm{r s}}=\frac{\mathrm{v}_{\mathrm{t}} \cdot(\mathrm{1 - \frac { \mathrm { C } _ { \mathrm { v s } } } { \mathrm { 0 . 1 7 5 \cdot ( 1 + \beta ) } } ) ^ { \beta }}}{\mathrm{v}_{\mathrm{l s}}}+\beta_{\mathrm{k}} \cdot \frac{\mathrm{v}_{\mathrm{t}}^{\mathrm{2}}}{\mathrm{v}_{\mathrm{l s}}^{\mathrm{2}}}\]
|
Dp=0.0254 m |
Dp=0.3 m |
Dp=1.2 m |
|
|
αk - T=10oC |
5.51 |
6.47 |
6.94 |
|
βk - T=10oC |
230.69 |
436.88 |
580.80 |
|
αk - T=20oC |
5.72 |
6.67 |
7.16 |
|
βk - T=20oC |
266.87 |
494.58 |
657.42 |
7.5.4.2 Simplified Model for Medium Sized Particles, 0.3 mm≤d≤2 mm
In terms of the transition range of particles, d=0.3 mm to about d=2 mm, based on the terminal settling velocity to the power 1.5 this gives:
\[\ \Delta \mathrm{E}_{\mathrm{s}, \mathrm{k i n}, \mathrm{p}}=\alpha_{\mathrm{t}}^{\mathrm{3} / 2} \cdot \mathrm{m}_{\mathrm{p}} \cdot \mathrm{v}_{\mathrm{t}}^{\mathrm{3 / 2}}=\mathrm{8 .5} \cdot \frac{\left(v_{\mathrm{l}} \cdot \mathrm{g}\right)^{1 / 3}}{\sqrt{\lambda_{\mathrm{l}}} \cdot \sqrt[4]{\mathrm{g} \cdot \mathrm{d}}} \cdot\left(\frac{\mathrm{v}_{\mathrm{t}}}{\sqrt{\mathrm{g} \cdot \mathrm{d}}}\right)^{\mathrm{1}} \cdot \mathrm{m} \cdot \mathrm{v}_{\mathrm{t}}^{\mathrm{3 / 2}}\]
The factor αt is now:
\[\ \mathrm{\alpha_{t}}=\left(8.5 \cdot \frac{\left(v_{\mathrm{l}} \cdot \mathrm{g}\right)^{1 / 3}}{\sqrt{\lambda_{\mathrm{l}}} \cdot \sqrt[4]{\mathrm{g \cdot d}}} \cdot\left(\frac{\mathrm{v_{t}}}{\sqrt{\mathrm{g \cdot d}}}\right)^{1}\right)^{2 / 3}\]
So for medium sized particles, the slip velocity can be determined as:
\[\ \mathrm{v}_{\mathrm{s l}}=\frac{\Delta \mathrm{E}_{\mathrm{s}, \mathrm{k i n}, \mathrm{p}}}{\mathrm{m}_{\mathrm{p}} \cdot \mathrm{v}_{\mathrm{l s}}}=\frac{\left(\alpha_{\mathrm{t}} \cdot \mathrm{v}_{\mathrm{t}}\right)^{\mathrm{3} / 2}}{\mathrm{v}_{\mathrm{l s}}}\]
This gives for the contribution of the kinetic energy losses to the excess hydraulic gradient Erhg, the Srs parameter, for particles from about d=0.3 mm to about d=2 mm as a first estimate:
\[\ \mathrm{S}_{\mathrm{r s}}=\left(\frac{\mathrm{v}_{\mathrm{s} \mathrm{l}}}{\mathrm{v}_{\mathrm{t}}}\right)^{2}=\left(\frac{\alpha_{\mathrm{t}}^{\mathrm{3 / 2}} \cdot \mathrm{v}_{\mathrm{t}}^{1 / 2}}{\mathrm{v}_{\mathrm{l s}}}\right)^{2}=\beta_{\mathrm{t}} \cdot \frac{\mathrm{v}_{\mathrm{t}}}{\mathrm{v}_{\mathrm{l} \mathrm{s}}^{2}}\]
|
Dp=0.0254 m |
Dp=0.3 m |
Dp=1.2 m |
|
|
αt - T=10oC |
2.42 |
3.00 |
3.29 |
|
βt - T=10oC |
14.19 |
26.87 |
35.72 |
|
αt - T=20oC |
2.41 |
2.96 |
3.25 |
|
βt - T=20oC |
13.95 |
25.84 |
34.35 |
The value of 2.97 is an average in the range d=0.3 mm to d=2 mm. In terms of the relative excess hydraulic gradient Erhg this gives:
\[\ \mathrm{E}_{\mathrm{r h g}}=\frac{\mathrm{i}_{\mathrm{m}}-\mathrm{i}_{\mathrm{l}}}{\mathrm{R}_{\mathrm{s d}} \cdot \mathrm{C}_{\mathrm{v s}}}=\mathrm{S}_{\mathrm{h r}}+\mathrm{S}_{\mathrm{r s}}=\frac{\mathrm{v}_{\mathrm{t}} \cdot(\mathrm{1 - \frac { \mathrm { C } _ { \mathrm { v s } } } { \mathrm { 0 . 1 7 5 \cdot ( 1 + \beta ) } } ) ^ { \beta }}}{\mathrm{v}_{\mathrm{l s}}}+\beta_{\mathrm{t}} \cdot \frac{\mathrm{v}_{\mathrm{t}}}{\mathrm{v}_{\mathrm{l s}}^{2}}\]
7.5.4.3 Simplified Model for Large Particles, d>2 mm
For large particles, d>2 mm, in terms of the momentum of a particle, based on the terminal settling velocity this gives:
\[\ \Delta \mathrm{E}_{\mathrm{s}, \mathrm{k i n}, \mathrm{p}}=\alpha_{\mathrm{m}} \cdot \mathrm{m}_{\mathrm{p}} \cdot \mathrm{v}_{\mathrm{t}}=\mathrm{8 .5} \cdot\left(\frac{v_{\mathrm{l}} \cdot \mathrm{g}}{\sqrt{\lambda_{\mathrm{l}}}}\right)^{1 / 3} \cdot\left(\frac{1}{\sqrt{\lambda_{\mathrm{l}}}}\right)^{2 / 3} \cdot\left(\frac{\mathrm{v}_{\mathrm{t}}}{\sqrt{\mathrm{g} \cdot \mathrm{d}}}\right)^{\mathrm{3} / \mathrm{2}} \cdot \mathrm{m} \cdot \mathrm{v}_{\mathrm{t}}\]
The factor αm is now:
\[\ \alpha_{\mathrm{m}}=8.5 \cdot\left(\frac{v_{1} \cdot \mathrm{g}}{\sqrt{\lambda_{\mathrm{l}}}}\right)^{1 / 3} \cdot\left(\frac{1}{\sqrt{\lambda_{\mathrm{l}}}}\right)^{2 / 3} \cdot\left(\frac{\mathrm{v}_{\mathrm{t}}}{\sqrt{\mathrm{g} \cdot \mathrm{d}}}\right)^{3 / 2}\]
So for large particles, the slip velocity can be determined as:
\[\ \mathrm{v}_{\mathrm{s l}}=\frac{\Delta \mathrm{E}_{\mathrm{s}, \mathrm{k i n}, \mathrm{p}}}{\mathrm{m}_{\mathrm{p}} \cdot \mathrm{v}_{\mathrm{l} \mathrm{s}}}=\alpha_{\mathrm{m}} \cdot \frac{\mathrm{v}_{\mathrm{t}}}{\mathrm{v}_{\mathrm{l} \mathrm{s}}}\]
This gives for the contribution of the kinetic energy looses to the excess hydraulic gradient Erhg, the Srs parameter, for large particles as a first estimate:
\[\ \mathrm{S}_{\mathrm{r s}}=\left(\frac{\mathrm{v}_{\mathrm{sl}}}{\mathrm{v}_{\mathrm{t}}}\right)^{2}=\left(\frac{\alpha_{\mathrm{m}}}{\mathrm{v}_{\mathrm{l s}}}\right)^{2}=\beta_{\mathrm{m}} \cdot \frac{\mathrm{1}}{\mathrm{v}_{\mathrm{l s}}^{2}}\]
In terms of the excess hydraulic gradient Erhg this gives:
\[\ \mathrm{E}_{\mathrm{rhg}}=\frac{\mathrm{i}_{\mathrm{m}}-\mathrm{i}_{\mathrm{l}}}{\mathrm{R}_{\mathrm{sd}} \cdot \mathrm{C}_{\mathrm{vs}}}=\mathrm{S}_{\mathrm{hr}}+\mathrm{S}_{\mathrm{rs}}=\frac{\mathrm{v}_{\mathrm{t}} \cdot\left(1-\frac{\mathrm{C}_{\mathrm{vs}}}{\mathrm{0 . 1 7 5} \cdot(\mathrm{1}+\beta)}\right)^{\beta}}{\mathrm{v}_{\mathrm{ls}}}+\beta_{\mathrm{m}} \cdot \frac{\mathrm{1}}{\mathrm{v}_{\mathrm{ls}}^{2}}\]
|
Dp=0.0254 m |
Dp=0.3 m |
Dp=1.2 m |
|
|
αm - T=10oC |
1.84 |
2.53 |
2.92 |
|
βm - T=10oC |
3.39 |
6.42 |
8.54 |
|
αm - T=20oC |
1.74 |
2.36 |
2.73 |
|
βm - T=20oC |
3.02 |
5.59 |
7.43 |
7.5.4.4 Summary Approximations
Figure 7.5-3 shows αk, αm and αt as a function of the particle diameter for a Dp=0.3 m pipe and T=10oC. From this figure it is obvious that for small particles (d<0.3 mm) the translational kinetic energy loss per interaction about equals a factor times the kinetic energy of the particle based on the terminal settling. For large particles (d>2 mm) the translational kinetic energy loss per interaction equals a factor times the momentum of the particle based on the terminal settling velocity. Apparently the losses of small particles are based on kinetic energy and the losses of large particles are based on momentum. This makes sense, since the small particles are smaller than the thickness of the viscous sub-layer, resulting in an interaction with the viscous sub-layer without any collision with the pipe wall. So the kinetic energy losses result from translational and rotational drag forces, which are proportional to velocity squared. For large particles on the other hand, the interactions will be dominated by collisions with the pipe wall. These particles will be much larger than the thickness of the viscous sub-layer, so there will not be much influence of the viscous sub-layer. Collisions with the pipe wall will also result in rotation of the particle and thus lift forces, but this is much more momentum based. For particles from about d=0.3 mm to about d=2 mm there is a transition area going from kinetic energy based losses to momentum based losses.
Independent of the assumption that the translational kinetic energy losses per interaction are independent from the line speed, it is obvious that for small particles (up to about d=0.3 mm) the excess head losses are proportional to the terminal settling velocity squared. For medium particles (from about d=0.3 mm to about d=2 mm) the excess head losses are proportional to the terminal settling velocity. For large particles (larger than about d=2 mm) the excess head losses are independent of the terminal settling velocity and thus the particle diameter. This also explains why different researchers found different relations based on the size of the particles used. The boundaries of d=0.3 mm and d=2 mm are an indication and depend on the kinematic viscosity νl, the relative submerged density Rsd and the Darcy-Weisbach friction factor λl (so also the pipe diameter Dp). For other powers of the line speed term, the proportionality coefficients will also be different.
7.5.4.5 Comparison with Durand & Condolios (1952)
Equation (7.5-62) is written in terms of known parameters like the line speed vls, the kinematic viscosity νl, the gravitational constant g, the terminal settling velocity vt, the particle diameter d and the Darcy-Weisbach friction factor λl, although it is derived from more fundamental parameters like the thickness of the viscous sub-layer δv and the velocity at the thickness of the viscous sub-layer 11.6·u* (angle of attack). Now knowing that the Darcy- Weisbach friction factor λl is reversely proportional to the line speed vsl and the pipe diameter Dp, both reversed to a power ranging from 0.15-0.2, this gives an additional proportionality for these parameters to a power of 0.15- 0.2. The resulting power of the line speed becomes this way -1.8 and the resulting power of the pipe diameter 0.2. The combination of the potential energy term being reversely proportional to the line speed with a power of -1 and the kinetic energy term being reversely proportional with the line speed to a power of -2, results in an additional increase of the power of the line speed by about 0.1 in the range of relevant line speeds.
The resulting power of the line speed in the kinetic energy term of about -2+0.2+0.1= -1.7 or -2+0.15+0.1=-1.75 is in between the power of -1.7 for uniform sands and gravels as found by Wilson et al. (1992) and the power of - 1.93 as found by Zandi & Govatos (1967). Wilson et al. (1992) state that the power of -1.7 in absolute terms is the maximum power, which is explained by the above reasoning. The power of 0.2 of the pipe diameter gives a weak dependency and can easily be overlooked if only experiments are carried out in a narrow range of pipe diameters like most researchers have done. The result of this is that most researchers did not find a correlation between the excess pressure losses and the pipe diameter. Durand & Condolios (1952), however did. Writing their equation in terms of the relative excess hydraulic gradient Erhg gives:
\[\ \begin{array}{left}\mathrm{E}_{\mathrm{r h g}}&=\frac{\mathrm{i}_{\mathrm{m}}-\mathrm{i}_{\mathrm{l}}}{\mathrm{R}_{\mathrm{s} \mathrm{d}} \cdot \mathrm{C}_{\mathrm{v} \mathrm{s}}}=\mathrm{1 3 .0 8}^{\mathrm{2}} \cdot \lambda_{\mathrm{l}} \cdot \mathrm{D}_{\mathrm{p}}^{\mathrm{1/2}} \cdot\left(\frac{\mathrm{v}_{\mathrm{t}}}{\sqrt{\mathrm{g} \cdot \mathrm{d}}}\right)^{\mathrm{1 0 / 3}} \cdot \frac{\mathrm{1}}{\mathrm{v}_{\mathrm{l s}}}\\
&\propto \mathrm{D}_{\mathrm{p}}^{-\mathrm{0 . 1 5}} \cdot \mathrm{v}_{\mathrm{l s}}^{-\mathrm{0 . 2}} \cdot \mathrm{D}_{\mathrm{p}}^{\mathrm{1 / 2}} \cdot\left(\frac{\mathrm{v}_{\mathrm{t}}}{\sqrt{\mathrm{g} \cdot \mathrm{d}}}\right)^{\mathrm{1 0 / 3}} \cdot \frac{\mathrm{1}}{\mathrm{v}_{\mathrm{l s}}}\end{array}\]
Applying the proportionalities between the Darcy-Weisbach friction factor λl and the line speed vls (-0.2) and the pipe diameter Dp (-0.15) gives for both equations:
\[\ \begin{array}{left} \mathrm{E}_{\mathrm{r h g}} \propto \mathrm{D}_{\mathrm{p}}^{\mathrm{0 . 3 5}} \cdot\left(\frac{\mathrm{v}_{\mathrm{t}}}{\sqrt{\mathrm{g} \cdot \mathrm{d}}}\right)^{\mathrm{1 0 / 3}} \cdot\left(\frac{\mathrm{1}}{\mathrm{v}_{\mathrm{l s}}}\right)^{\mathrm{1 . 2}} \quad\mathrm{v s .}\quad \mathrm{E}_{\mathrm{r h g}} \propto \mathrm{D}_{\mathrm{p}}^{0 .1 5} \cdot\left(\frac{\mathrm{v}_{\mathrm{t}}}{\sqrt{\mathrm{g} \cdot \mathrm{d}}}\right)^{\mathrm{1 0 / 3}} \cdot\left(\frac{\mathrm{1}}{\mathrm{v}_{\mathrm{l s}}}\right)^{\mathrm{1 . 7}}\\
\quad\quad \quad\text{Durand & Condolios}\quad\quad\quad\quad\quad\quad\quad\quad\quad \text{DHLLDV}\end{array}\]
Of course the potential energy term is not taken into account here separately, because Durand & Condolios (1952) did not take it into account, however it is taken into account by reducing the power of the line speed. Still both equations show a large similarity. It should be mentioned that the power of the particle Froude number is the same in both equations, since this power has been derived from the Gibert (1960) graph. The power of the pipe diameter differs by a power of 0.2, explaining why the Durand & Condolios (1952) equation overestimates the pressure losses in large diameter pipes. The power of the line speed differs, since Durand & Condolios (1952) considered both uniform and non-uniform sands and gravels, while here (DHLLDV) only uniform sands and gravels are considered. For small and medium sized pipes both models are very close in the neighborhood of the intersection of the heterogeneous and homogeneous regimes
7.5.5 The Slip Velocity Applied to the Fuhrboter Equation
Now suppose the reversed proportionality with the line speed is 0.5 for the slip velocity and 1 for the relative excess hydraulic gradient, like many researchers have found for non-uniform sands and gravels, then what would the equations look like, matching the experiments from literature as good as possible? First the equations for the translational kinetic energy losses are modified, based on keeping the transition of the heterogeneous regime to the homogeneous regime at the same line speed and a power of the particle Froude number of 3:
\[\ \Delta \mathrm{E}_{\mathrm{s}, \mathrm{k i n}, \mathrm{p}}=\mathrm{1 .7 5} \cdot \mathrm{m}_{\mathrm{p}} \cdot\left(\frac{\delta_{\mathrm{v}}}{\mathrm{d}}\right)^{1 / 6} \cdot\left(\frac{\mathrm{v}_{\mathrm{t}}}{\mathrm{1 1 .6} \cdot \mathrm{u}_{*}}\right)^{1 / \mathrm{3}} \cdot\left(\frac{\mathrm{v}_{\mathrm{t}}}{\sqrt{\mathrm{g} \cdot \mathrm{d}}}\right)^{7 / \mathrm{6}} \cdot \mathrm{v}_{\mathrm{t}} \cdot \mathrm{v}_{\mathrm{ls}}\]
\[\ \Delta \mathrm{E}_{\mathrm{s}, \mathrm{k i n}, \mathrm{p}}=\mathrm{1 .7 5} \cdot \mathrm{m}_{\mathrm{p}} \cdot\left(\frac{\mathrm{3 2 .8 1}}{\mathrm{4 .1}^{\mathrm{2}}}\right)^{1 / 6} \cdot\left(\frac{\mathrm{1}}{\sqrt{\lambda_{\mathrm{l}}}}\right)^{1 / 2} \cdot\left(\frac{\mathrm{v}_{\mathrm{t}}}{\sqrt{\mathrm{g} \cdot \mathrm{d}}}\right)^{3 / 2} \cdot\left(\frac{\left(v_{\mathrm{l}} \cdot \mathrm{g}\right)^{1 / 3}}{\mathrm{v}_{\mathrm{l s}}}\right)^{1 / 2} \cdot \mathrm{v}_{\mathrm{t}} \cdot \mathrm{v}_{\mathrm{l} \mathrm{s}}\]
The above equations give for the slip velocity, Miedema & Ramsdell (2013):
\[\ \mathrm{v}_{\mathrm{s l}}=\frac{\Delta \mathrm{E}_{\mathrm{s}, \mathrm{k i n}, \mathrm{p}}}{\mathrm{m}_{\mathrm{p}} \cdot \mathrm{v}_{\mathrm{ls}} }=\mathrm{1 . 7 5} \cdot\left(\frac{\delta_{\mathrm{v}}}{\mathrm{d}}\right)^{1 / 6} \cdot\left(\frac{\mathrm{v}_{\mathrm{t}}}{\mathrm{1 1 .6} \cdot \mathrm{u}_{*}}\right)^{1 / 3} \cdot\left(\frac{\mathrm{v}_{\mathrm{t}}}{\sqrt{\mathrm{g} \cdot \mathrm{d}}}\right)^{7 / \mathrm{6}} \cdot \mathrm{v}_{\mathrm{t}}\]
Or:
\[\ \mathrm{v}_{\mathrm{s l}}=\mathrm{1 .7 5} \cdot\left(\frac{\mathrm{3 2 . 8 1}}{\mathrm{4 .1}^{\mathrm{2}}}\right)^{1 / 6} \cdot\left(\frac{\mathrm{1}}{\sqrt{\lambda_{\mathrm{l}}}}\right)^{1 / 2} \cdot\left(\frac{\mathrm{v}_{\mathrm{t}}}{\sqrt{\mathrm{g} \cdot \mathrm{d}}}\right)^{3 / 2} \cdot\left(\frac{\left(v_{\mathrm{l}} \cdot \mathrm{g}\right)^{1 / 3}}{\mathrm{v}_{\mathrm{l s}}}\right)^{1 / 2} \cdot \mathrm{v}_{\mathrm{t}}\]
This gives for the relative excess hydraulic gradient:
\[\ \mathrm{E}_{\mathrm{rhg}}=\frac{\mathrm{i}_{\mathrm{m}}-\mathrm{i}_{\mathrm{l}}}{\mathrm{R}_{\mathrm{sd}} \cdot \mathrm{C}_{\mathrm{vs}}}=\mathrm{S}_{\mathrm{hr}}+\mathrm{S}_{\mathrm{rs}}=\frac{\mathrm{v}_{\mathrm{t}} \cdot\left(\mathrm{1}-\frac{\mathrm{C}_{\mathrm{vs}}}{\mathrm{\kappa}_{\mathrm{C}}}\right)^{\beta}}{\mathrm{v}_{\mathrm{ls}}}+2.19^{2} \cdot\left(\frac{\mathrm{1}}{\sqrt{\lambda_{\mathrm{l}}}}\right) \cdot\left(\frac{\mathrm{v}_{\mathrm{t}}}{\sqrt{\mathrm{g} \cdot \mathrm{d}}}\right)^{3} \cdot\left(\frac{\left(v_{\mathrm{l}} \cdot \mathrm{g}\right)^{1 / 3}}{\mathrm{v}_{\mathrm{ls}}}\right)^1\]
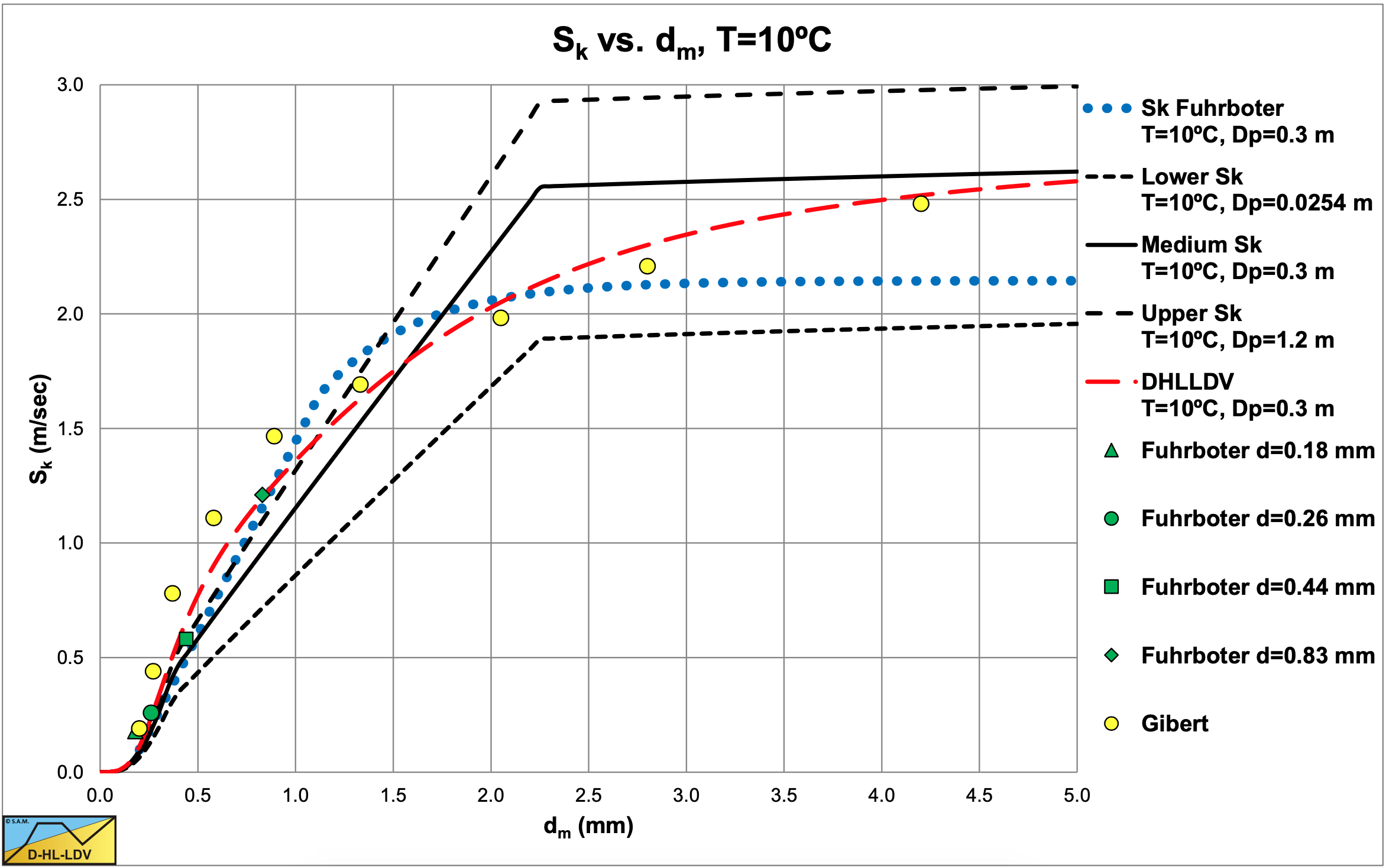
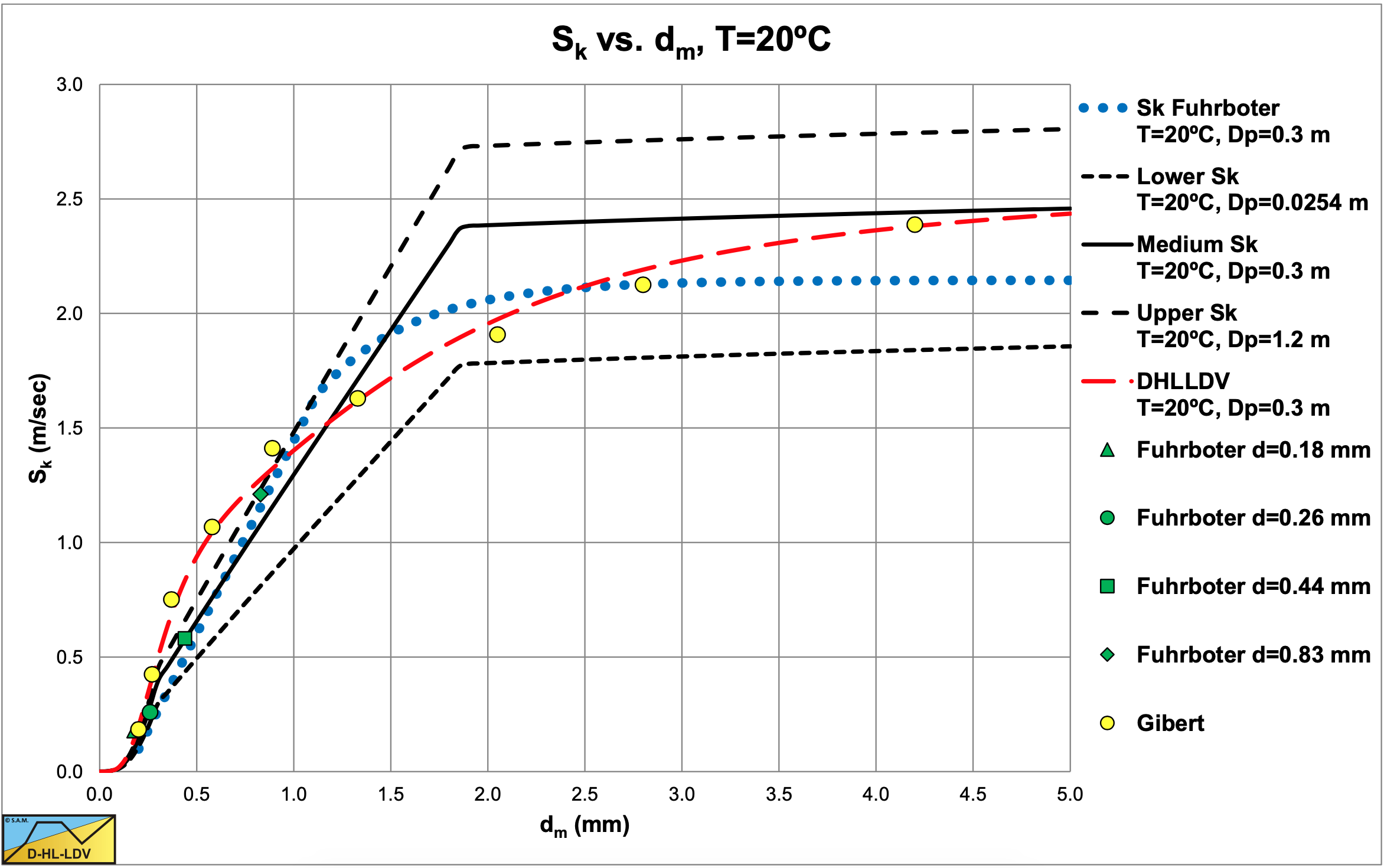
Figure 7.5-4 shows the 3 coefficients as a function of the particle diameter for a Dp=0.3 m pipe and T=10oC, while Table 7.5-5 shows the viscosities and Darcy Weisbach friction factors used here. Fuhrboter (1961) found a Darcy- Weisbach friction factor λl=0.014. Since for very small particles (Stokes region) the terminal settling velocity is proportional with the particle diameter squared, the Srs value and thus the Sk value is proportional with the particle diameter to the 4th power. This is the reason of the starting point of the original Sk curve at a particle diameter of 0.2 mm.
|
Viscosity (m2/s) |
Dp=0.0254 m |
Dp=0.3 m |
Dp=1.2 m |
|
|
T=10oC |
0.0000013 |
0.0214 |
0.0113 |
0.0085 |
|
T=20oC |
0.0000010 |
0.0202 |
0.0109 |
0.0082 |
7.5.5.1 Simplified Model for Small Particles, d<0.3 mm
In terms of the kinetic translational energy of a particle based on the terminal settling velocity for small particles, the following expression can be found:
\[\ \begin{array}{left}\Delta \mathrm{E}_{\mathrm{s}, \mathrm{k i n}, \mathrm{p}}&=\frac{\mathrm{1}}{\mathrm{2}} \cdot \mathrm{m}_{\mathrm{p}} \cdot\left(\alpha_{\mathrm{k}} \cdot \mathrm{v}_{\mathrm{t}}\right)^{2} \cdot \mathrm{v}_{\mathrm{l s}}^{1 / 2}\\
&=\mathrm{2} \cdot \mathrm{1.7 5} \cdot\left(\frac{\mathrm{3 2 . 8 1} \cdot v_{\mathrm{l}} \cdot \mathrm{g}}{\mathrm{4 .1}^{\mathrm{2}}}\right)^{\mathrm{1 / 6}} \cdot\left(\frac{\mathrm{1}}{\sqrt{\lambda_{\mathrm{l}}}}\right)^{1/2} \cdot\left(\frac{\mathrm{v}_{\mathrm{t}}}{\sqrt{\mathrm{g} \cdot \mathrm{d}}}\right)^{1 / 2} \cdot\left(\frac{\mathrm{1}}{\sqrt{\mathrm{g} \cdot \mathrm{d}}}\right)^{1} \cdot \mathrm{v}_{\mathrm{l} \mathrm{s}}^{1 / 2} \cdot \frac{\mathrm{1}}{\mathrm{2}} \cdot \mathrm{m}_{\mathrm{p}} \cdot \mathrm{v}_{\mathrm{t}}^{\mathrm{2}}\end{array}\]
The factor αk is now:
\[\ \alpha_{k}=\sqrt{2 \cdot 1.75 \cdot\left(\frac{32.81 \cdot v_{\mathrm{l}} \cdot \mathrm{g}}{4.1^{2}}\right)^{1 / 6} \cdot\left(\frac{1}{\sqrt{\lambda_{\mathrm{l}}}}\right)^{1 / 2} \cdot\left(\frac{\mathrm{v_{t}}}{\sqrt{\mathrm{g \cdot d}}}\right)^{1 / 2} \cdot\left(\frac{1}{\sqrt{\mathrm{g \cdot d}}}\right)^{1}}\]
This gives for the contribution of the kinetic energy losses to the relative excess hydraulic gradient Erhg, the Srs parameter, for very small particles as a first estimate:
\[\ \mathrm{S}_{\mathrm{r s}}=\left(\frac{\mathrm{v}_{\mathrm{s} \mathrm{l}}}{\mathrm{v}_{\mathrm{t}}}\right)^{2}=\left(\frac{\alpha_{\mathrm{k}}^{2}}{\mathrm{2}} \cdot \frac{\mathrm{v}_{\mathrm{t}}}{\mathrm{v}_{\mathrm{l} \mathrm{s}}^{1 / 2}}\right)^{2}=\beta_{\mathrm{k}} \cdot \frac{\mathrm{v}_{\mathrm{t}}^{2}}{\mathrm{v}_{\mathrm{ls}}}\]
In terms of the relative excess hydraulic gradient Erhg this gives:
\[\ \mathrm{E}_{\mathrm{r h g}}=\frac{\mathrm{i}_{\mathrm{m}}-\mathrm{i}_{\mathrm{l}}}{\mathrm{R}_{\mathrm{s d}} \cdot \mathrm{C}_{\mathrm{v s}}}=\mathrm{S}_{\mathrm{h r}}+\mathrm{S}_{\mathrm{r s}}=\frac{\mathrm{v}_{\mathrm{t}} \cdot \left(\mathrm{1 - \frac { \mathrm { C } _ { \mathrm { v s } } } { \mathrm { \kappa } _ { \mathrm { C } } }}\right)^{\beta}}{\mathrm{v}_{\mathrm{l s}}}+\beta_{\mathrm{k}} \cdot \frac{\mathrm{v}_{\mathrm{t}}^{\mathrm{2}}}{\mathrm{v}_{\mathrm{l s}}}\]
|
Dp=0.0254 m |
Dp=0.3 m |
Dp=1.2 m |
|
|
αk - T=10oC |
4.18 |
4.53 |
4.69 |
|
βk - T=10oC |
76.55 |
105.34 |
121.46 |
|
αk - T=20oC |
4.40 |
4.76 |
4.93 |
|
βk - T=20oC |
93.90 |
127.83 |
147.38 |
7.5.5.2 Simplified Model for Medium Sized Particles, 0.3 mm≤d≤2 mm
In terms of the transition range of particles based on the terminal settling velocity to the power 1.5 this gives:
\[\ \begin{array}{left}\Delta \mathrm{E}_{\mathrm{s}, \mathrm{k i n}, \mathrm{p}}&=\mathrm{m}_{\mathrm{p}} \cdot\left(\alpha_{\mathrm{t}} \cdot \mathrm{v}_{\mathrm{t}}\right)^{3 / 2} \cdot \mathrm{v}_{\mathrm{l} \mathrm{s}}^{1 / 2}\\
&=\mathrm{1 .7 5} \cdot\left(\frac{\mathrm{3} \mathrm{2 . 8 1} \cdot v_{\mathrm{l}} \cdot \mathrm{g}}{\mathrm{4 . 1}^{\mathrm{2}}}\right)^{1 / 6} \cdot\left(\frac{\mathrm{1}}{\sqrt{\lambda_{\mathrm{l}}}}\right)^{1 / 2} \cdot\left(\frac{\mathrm{1}}{\sqrt{\mathrm{g} \cdot \mathrm{d}}}\right)^{1 / 2} \cdot\left(\frac{\mathrm{v}_{\mathrm{t}}}{\sqrt{\mathrm{g} \cdot \mathrm{d}}}\right)^{1} \cdot \mathrm{v}_{\mathrm{l} \mathrm{s}}^{1 / 2} \cdot \mathrm{m}_{\mathrm{p}} \cdot \mathrm{v}_{\mathrm{t}}^{\mathrm{3} / 2}\end{array}\]
The factor αt is now:
\[\ \alpha_{\mathrm{t}}=\left(1.75 \cdot\left(\frac{32.81 \cdot v_{\mathrm{l}} \cdot \mathrm{g}}{4.1^{2}}\right)^{1 / 6} \cdot\left(\frac{1}{\sqrt{\lambda_{\mathrm{l}}}}\right)^{1 / 2} \cdot\left(\frac{1}{\sqrt{\mathrm{g \cdot d}}}\right)^{1 / 2} \cdot\left(\frac{\mathrm{v_{t}}}{\sqrt{\mathrm{g \cdot d}}}\right)^{1}\right)^{2 / 3}\]
This gives for the contribution of the kinetic energy losses to the relative excess hydraulic gradient Erhg, the Srs parameter, for particles from about d=0.3 mm to about d=2 mm as a first estimate:
\[\ \mathrm{S}_{\mathrm{r} \mathrm{s}}=\left(\frac{\mathrm{v}_{\mathrm{s} \mathrm{l}}}{\mathrm{v}_{\mathrm{t}}}\right)^{2}=\left(\frac{\alpha_{\mathrm{t}}^{\mathrm{3} / 2} \cdot \mathrm{v}_{\mathrm{t}}^{1 / 2}}{\mathrm{v}_{\mathrm{l} \mathrm{s}}^{\mathrm{1} / 2}}\right)^{2}=\beta_{\mathrm{t}} \cdot \frac{\mathrm{v}_{\mathrm{t}}}{\mathrm{v}_{\mathrm{ls}}}\]
In terms of the relative excess hydraulic gradient Erhg this gives:
\[\ \mathrm{E}_{\mathrm{rhg}}=\frac{\mathrm{i}_{\mathrm{m}}-\mathrm{i}_{\mathrm{l}}}{\mathrm{R}_{\mathrm{sd}} \cdot \mathrm{C}_{\mathrm{vs}}}=\mathrm{S}_{\mathrm{hr}}+\mathrm{S}_{\mathrm{rs}}=\frac{\mathrm{v}_{\mathrm{t}} \cdot\left(\mathrm{1}-\frac{\mathrm{C}_{\mathrm{vs}}}{\mathrm{\kappa}_{\mathrm{C}}}\right)^{\beta}}{\mathrm{v}_{\mathrm{l s}}}+\beta_{\mathrm{t}} \cdot \frac{\mathrm{v}_{\mathrm{t}}}{\mathrm{v}_{\mathrm{l s}}}\]
|
Dp=0.0254 m |
Dp=0.3 m |
Dp=1.2 m |
|
|
αt - T=10oC |
1.68 |
1.86 |
1.95 |
|
βt - T=10oC |
4.71 |
6.48 |
7.47 |
|
αt - T=20oC |
1.70 |
1.88 |
1.97 |
|
βt - T=20oC |
4.91 |
6.68 |
7.70 |
7.5.5.3 Simplified Model for Large Particles, d>2 mm
In terms of the momentum of a particle based on the terminal settling velocity for large particles this gives:
\[\ \Delta \mathrm{E}_{\mathrm{s}, \mathrm{k i n}, \mathrm{p}}=\mathrm{m}_{\mathrm{p}} \cdot\left(\alpha_{\mathrm{m}} \cdot \mathrm{v}_{\mathrm{t}}\right) \cdot \mathrm{v}_{\mathrm{l} \mathrm{s}}^{1 / 2}=\mathrm{1 . 7 5} \cdot\left(\frac{\mathrm{3 2 . 8 1} \cdot v_{\mathrm{l}} \cdot \mathrm{g}}{4.1^{2}}\right)^{1 / 6} \cdot\left(\frac{1}{\sqrt{\lambda_{\mathrm{l}}}}\right)^{1 / 2} \cdot\left(\frac{\mathrm{v}_{\mathrm{t}}}{\sqrt{\mathrm{g} \cdot \mathrm{d}}}\right)^{\mathrm{3} / 2} \cdot \mathrm{v}_{\mathrm{l} \mathrm{s}}^{1 / 2} \cdot \mathrm{m}_{\mathrm{p}} \cdot \mathrm{v}_{\mathrm{t}}\]
The factor αm is now:
\[\ \alpha_{\mathrm{m}}=1.65 \cdot\left(\frac{32.81 \cdot v_{\mathrm{l}} \cdot \mathrm{g}}{4.1^{2}}\right)^{1 / 6} \cdot\left(\frac{1}{\sqrt{\lambda_{\mathrm{l}}}}\right)^{1 / 2} \cdot\left(\frac{\mathrm{v_{t}}}{\sqrt{\mathrm{g \cdot d}}}\right)^{4 / 3}\]
This gives for the contribution of the kinetic energy losses to the relative excess hydraulic gradient Erhg, the Srs parameter, for very large particles as a first estimate:
\[\ \mathrm{S}_{\mathrm{r s}}=\left(\frac{\mathrm{v}_{\mathrm{s} \mathrm{l}}}{\mathrm{v}_{\mathrm{t}}}\right)^{2}=\left(\frac{\alpha_{\mathrm{m}}}{\mathrm{v}_{\mathrm{l} \mathrm{s}}^{1/ 2}}\right)^{2}=\beta_{\mathrm{m}} \cdot \frac{\mathrm{1}}{\mathrm{v}_{\mathrm{ls}}}\]
In terms of the relative excess hydraulic gradient Erhg this gives:
\[\ \mathrm{E}_{\mathrm{rhg}}=\frac{\mathrm{i}_{\mathrm{m}}-\mathrm{i}_{\mathrm{l}}}{\mathrm{R}_{\mathrm{sd}} \cdot \mathrm{C}_{\mathrm{vs}}}=\mathrm{S}_{\mathrm{hr}}+\mathrm{S}_{\mathrm{rs}}=\frac{\mathrm{v}_{\mathrm{t}} \cdot\left(1-\frac{\mathrm{C}_{\mathrm{vs}}}{\mathrm{\kappa}_{\mathrm{C}}}\right)^{\beta}}{\mathrm{v}_{\mathrm{ls}}}+\beta_{\mathrm{m}} \cdot \frac{\mathrm{1}}{\mathrm{v}_{\mathrm{ls}}}\]
|
Dp=0.0254 m |
Dp=0.3 m |
Dp=1.2 m |
|
|
αm - T=10oC |
1.06 |
1.24 |
1.33 |
|
βm - T=10oC |
1.11 |
1.53 |
1.77 |
|
αm - T=20oC |
1.03 |
1.20 |
1.28 |
|
βm - T=20oC |
1.05 |
1.44 |
1.65 |
7.5.5.4 Summary Approximations
The above equations are quite similar to the Fuhrboter (1961) approach. If the potential energy term is neglected and taking into consideration that the equations are derived for a constant spatial volumetric concentration, while Fuhrboter (1961) corrected for a ratio of 0.65 between the constant delivered concentration and the constant spatial concentration and further assuming that in the transition region the terminal settling velocity is about 105-115 times the particle diameter, the following relations can be derived for the Sk parameter of Fuhrboter (1961):
\[\ \mathrm{S}_{\mathrm{k}}=\mathrm{E}_{\mathrm{r h g}} \cdot \mathrm{R}_{\mathrm{s d}}=\left(\mathrm{S}_{\mathrm{h r}}+\mathrm{S}_{\mathrm{r s}}\right) \cdot \mathrm{R}_{\mathrm{s d}}\]
It should be mentioned that the particle diameter in these equations is in m, while Fuhrboter (1961) used the particle diameter in mm in his equations. Figure 7.5-5 shows the original Sk curve of Fuhrboter (1961) and the estimated curves, based on the kinetic energy approach, with upper and lower limits. The resemblance of the Fuhrboter curve with the average curve as derived here is remarkable. Only for very small particles the original curve gives smaller Sk values. The data points have been recalculated, based on the original data of Fuhrboter (1961), giving slightly higher values, matching the theoretical and approximation curves, except for the 0.83 mm particles. The latter could be caused by the non-uniform PSD of this sand.
However the difference between the lower and upper limit is large. Fuhrboter (1961) carried out his experiments in a 0.3 m pipe, which is close to the average curve. For the full range of particle diameters the contribution of the translational kinetic energy losses, the Srs parameter, is:
\[\ \mathrm{S}_{\mathrm{r} \mathrm{s}}=\left(\frac{\mathrm{v}_{\mathrm{sl}}}{\mathrm{v}_{\mathrm{t}}}\right)^{2}=\mathrm{2} . \mathrm{1} \mathrm{9}^{2} \cdot\left(\frac{\mathrm{1}}{\sqrt{\lambda_{\mathrm{l}}}}\right) \cdot\left(\frac{\mathrm{v}_{\mathrm{t}}}{\sqrt{\mathrm{g} \cdot \mathrm{d}}}\right)^{\mathrm{1 0 / 3}} \cdot\left(\frac{\left(v_{\mathrm{l}} \cdot \mathrm{g}\right)^{1 / 3}}{\mathrm{v}_{\mathrm{l s}}}\right)^{\mathrm{1}}\]
Giving for the relative excess hydraulic gradient, the Erhg parameter:
\[\ \mathrm{E}_{\mathrm{rhg}}=\frac{\mathrm{i}_{\mathrm{m}}-\mathrm{i}_{\mathrm{l}}}{\mathrm{R}_{\mathrm{sd}} \cdot \mathrm{C}_{\mathrm{vs}}}=\mathrm{S}_{\mathrm{hr}}+\mathrm{S}_{\mathrm{rs}}=\frac{\mathrm{v}_{\mathrm{t}} \cdot\left(1-\frac{\mathrm{C}_{\mathrm{vs}}}{\mathrm{\kappa}_{\mathrm{C}}}\right)^{\beta}}{\mathrm{v}_{\mathrm{ls}}}+2.19^{2} \cdot\left(\frac{\mathrm{1}}{\sqrt{\lambda_{\mathrm{l}}}}\right) \cdot\left(\frac{\mathrm{v}_{\mathrm{t}}}{\sqrt{\mathrm{g} \cdot \mathrm{d}}}\right)^{10 / 3} \cdot\left(\frac{\left(v_{\mathrm{l}} \cdot \mathrm{g}\right)^{1 / 3}}{\mathrm{v}_{\mathrm{ls}}}\right)^1\]
Equation (7.5-62) is derived for uniform sands and gravels, while equation (7.5-100) is suitable for non-uniform sands and gravels, matching equations of different researchers. Both equations give about the same intersection point with the homogeneous regime and also give about the same pressure losses at line speeds around that intersection point. The Sk factor can be approached for all particle diameters according to the following equation as is also shown in Figure 7.5-5:
\[\ \mathrm{S}_{\mathrm{k}}=\left(\mathrm{v}_{\mathrm{t}} \cdot\left(\mathrm{1}-\frac{\mathrm{C}_{\mathrm{v s}}}{\mathrm{\kappa}_{\mathrm{C}}}\right)^{\beta}+\mathrm{2.19} ^{2} \cdot\left(\frac{\mathrm{1}}{\sqrt{\lambda_{\mathrm{l}}}}\right) \cdot\left(\frac{\mathrm{v}_{\mathrm{t}}}{\sqrt{\mathrm{g} \cdot \mathrm{d}}}\right)^{\mathrm{1 0 / 3}} \cdot\left(v_{\mathrm{l}} \cdot \mathrm{g}\right)^{1 / 3}\right) \cdot \mathrm{R}_{\mathrm{s d}}\]
7.5.6 The Concentration Eccentricity Coefficient
The concentration eccentricity coefficient κC tells what the concentration profile looks like. If the concentration profile is symmetrical with respect to the center of the pipe the coefficient has a value of 1. This will be the case with very small particles and homogeneous flow. With coarse particles however the mean position of the particles will be below the center of the pipe, so the coefficient will have a value smaller than 1. The potential energy term contains the following term, which is also used in the LDV equations:
\[\ \left(1-\frac{\mathrm{C}_{\mathrm{v s}}}{\mathrm{\kappa}_{\mathrm{C}}}\right)^{\beta} \cdot \mathrm{C}_{\mathrm{v s}}\]
It is known from literature that the LDV has a maximum for a concentration in the range 15%-20%. This is only possible if this term has a maximum in this range. To find this maximum, the derivative with respect to the concentration is taken:
\[\ \begin{array}{left} \frac{\mathrm{d}}{\mathrm{d} \mathrm{C}_{\mathrm{v s}}}\left(\left(\mathrm{1}-\frac{\mathrm{C}_{\mathrm{v s}}}{\mathrm{\kappa}_{\mathrm{C}}}\right)^{\beta} \cdot \mathrm{C}_{\mathrm{v s}}\right)=\left(\mathrm{1}-\frac{\mathrm{C}_{\mathrm{v s}}}{\mathrm{\kappa}_{\mathrm{C}}}\right)^{\beta}-\frac{\mathrm{C}_{\mathrm{v} s} \cdot \boldsymbol{\beta}}{\mathrm{\kappa}_{\mathrm{C}}} \cdot\left(\mathrm{1}-\frac{\mathrm{C}_{\mathrm{v} \mathrm{s}}}{\mathrm{k}_{\mathrm{C}}}\right)^{\beta-\mathrm{1}}\\
\left(1-\frac{\mathrm{C}_{\mathrm{vs}, \max }}{\kappa_{\mathrm{C}}}\right)^{\beta-1} \cdot\left(\left(1-\frac{\mathrm{C}_{\mathrm{vs}, \max }}{\kappa_{\mathrm{C}}}\right)-\frac{\mathrm{C}_{\mathrm{vs}, \max } \cdot \beta}{\kappa_{\mathrm{C}}}\right)=0 \quad\Rightarrow \quad 1-\frac{\mathrm{C}_{\mathrm{vs}, \max }}{\kappa_{\mathrm{C}}} \cdot(1+\beta)=0\\
\mathrm{\kappa_{C}=C_{v s, \max } \cdot(1+\beta) \quad\text{ or }\quad C_{v s, \max }=\frac{\kappa_{C}}{(1+\beta)}}\end{array}\]
The concentration eccentricity coefficient is a function of the concentration where the maximum occurs and vice versa. Since κC can never be larger than 1 for homogeneous flow, the concentration where the maximum occurs only depends on the hindered settling power β. This power has a maximum of 4.7 for very small particles, according to Richardson & Zaki (1954). This results in a concentration where the maximum occurs of 17.5%, exactly in the middle of the range where the maximum LDV is observed. This gives for the concentration eccentricity coefficient κC:
\[\ \mathrm{\kappa_{C}=0.175 \cdot(1+\beta)}\]
For very large particles with a hindered settling power of about 2.4, this gives a concentration eccentricity coefficient of 0.595. This is about 60% of the radius of the pipe measured from the bottom of the pipe, which seems reasonable.
7.5.7 Discussion & Validation
Until now papers of the following researchers have been used to analyze, verify and validate the new theory regarding the head loss curves: Blatch (1906), O’Brien & Folsom (1939), Soleil & Ballade (1952), Durand & Condolios (1952), Newitt et al. (1955), Worster & Denny. (1955), Gibert (1960), Fuhrboter (1961), Silin & Kobernik (1962), Thomas (1965), Zandi & Govatos (1967), Wiedenroth (1967), Fowkes & Wancheck (1969), Babcock (1970), Graf et al. (1970), Yagi et al. (1972), Karasik (1973), Kazanskij (1978), Boothroyde et al. (1979), Kazanskij (1980), Clift et al. (1982), Scheurel (1985), Doron et al. (1987), Gillies (1993), Blythe & Czarnotta (1995), Doron et al. (1995), Matousek (1997), Schaan et al. (2000), Matousek (2004), Gillies et al. (2004), Whitlock et al. (2004), Ni et al. (2004), Ming et al. (2007), Ni et al. (2008), Vlasak (2008), Ravelet et al. (2012) and Vlasak et al. (2012). Because of the enormous amount of data it is not possible to show everything, so a selection of graphs giving the essence of the verification and validation will be shown.
Figure 7.1-7 & Figure 7.1-8 already show a good correlation between the new heterogeneous regime model and the experiments of Clift et al. (1982) for a medium d=0.68 mm sand and medium pipe diameters of Dp=0.2 m and Dp=0.44 m.
Figure 7.5-7 & Figure 7.5-8 show data of Durand & Condolios (1952) as published by Gibert (1960) with particles ranging from a diameter of d=0.2 mm up to d=4.2 mm in a pipe with a diameter of Dp=0.15 m.
Figure 7.5-9 shows data of Whitlock et al. (2004) with particles ranging from a diameter of d=0.085 mm up to d=0.4 mm in a pipe with a diameter of Dp=0.1 m.
Figure 7.5-10 shows data of Clift et al. (1982) with particles with a diameter d=0.6 mm in a pipe with a diameter of Dp=0.49 m.
More Graphs can be found in Miedema (2013) and Ramsdell & Miedema (2013) and in other chapters.
For the interpretation of the graphs one should realize that for dredging practice pipe diameters of 0.1 or 0.15 m or even smaller are not really representative for dredging using diameters up to 1.2 m. Although the graphs show a good correlation between the experiments and the theoretical lines, to make the theory appropriate for dredging practice, there should be evidence that there is also a good correlation for the larger pipe diameters. That’s the reason why some graphs are added for pipe diameters up to Dp=0.49 m and even larger. Figure 7.1-8 and Figure 7.5-10 show some of these experiments.
All the graphs show a good correlation between the experiments and the theoretical curves, but they show more. All the graphs show that there is an intersection between heterogeneous and homogeneous transport regimes, but often the experiments continue to excess pressures below the homogeneous curve and at higher line speeds tend to move into the direction of the homogeneous curve. The graphs also show that this specifically occurs for medium sized particles. Very small particles follow the heterogeneous curve and then bend to the homogeneous curve. Large particles will probably follow the sliding bed curve and from there continue with (pseudo) heterogeneous transport at very high line speeds. In dredging practice it is known that very small particles behave homogeneous. For medium sized particles it is assumed that they follow the water resistance curve, while larger particles will have excess pressure. This is explained with the graphs shown here.
Another phenomenon that is shown in Figure 7.5-7 & Figure 7.5-8 is the transition between the sliding bed regime and the heterogeneous regime for the d=2.05 mm and the d=4.20 mm particles. In both cases the data points lie on or above the theoretical curves at higher line speeds, but below the curves at low line speeds, close to the sliding bed curve. The smaller particles do not show this kind of behavior, but then the hydraulic gradients of the smaller particles are much smaller.
Last but not least Figure 7.5-10 shows clearly that below the Limit Deposit Velocity, the data points continue to follow the theoretical curve for heterogeneous transport (the Limit Deposit Velocity is at about iw=0.02-0.03). This has also been observed by Durand & Condolios (1952) and Zandi & Govatos (1967).
The new approach of modeling head losses in slurry transport based on energy considerations, giving 3 terms for the head losses, correlates well with many experiments. In the head loss equation 3 terms can be distinguished, the viscous friction losses, the potential energy losses and the kinetic energy losses. The kinetic energy losses are based on the slip velocity required to explain these losses.
Introducing three new dimensionless numbers, the Durand & Condolios (1952) Froude number Cát, Ct (Vietnamese for sand grains), the Lắng number La (Lắng is Vietnamese for sediment) and the Thủy number Th (Thủy is Vietnamese for aquatic, water) simplifies the resulting equations.
The Durand & Condolios (1952) particle Froude number Ct giving the contribution of the solids to the excess head losses, the collision impact, is:
\[\ \mathrm{Ct}=\left(\mathrm{Fr}_{\mathrm{p}}\right)^{5 / 3}=\left(\frac{1}{\sqrt{\mathrm{C}_{\mathrm{x}}}}\right)^{5 / 3}\]
The new Thủy number (Th) is the cube root of the ratio of the viscous forces times the gravitational forces to the inertial forces squared. The Thủy number gives the contribution of the liquid flow, in dredging applications water, to the excess head losses, the collision intensity. Defining the Thủy number (Th) to:
\[\ \mathrm{T h}=\left(\frac{v_{\mathrm{l}} \cdot \mathrm{g}}{\mathrm{v^{3}}}\right)^{1 / 3}\]
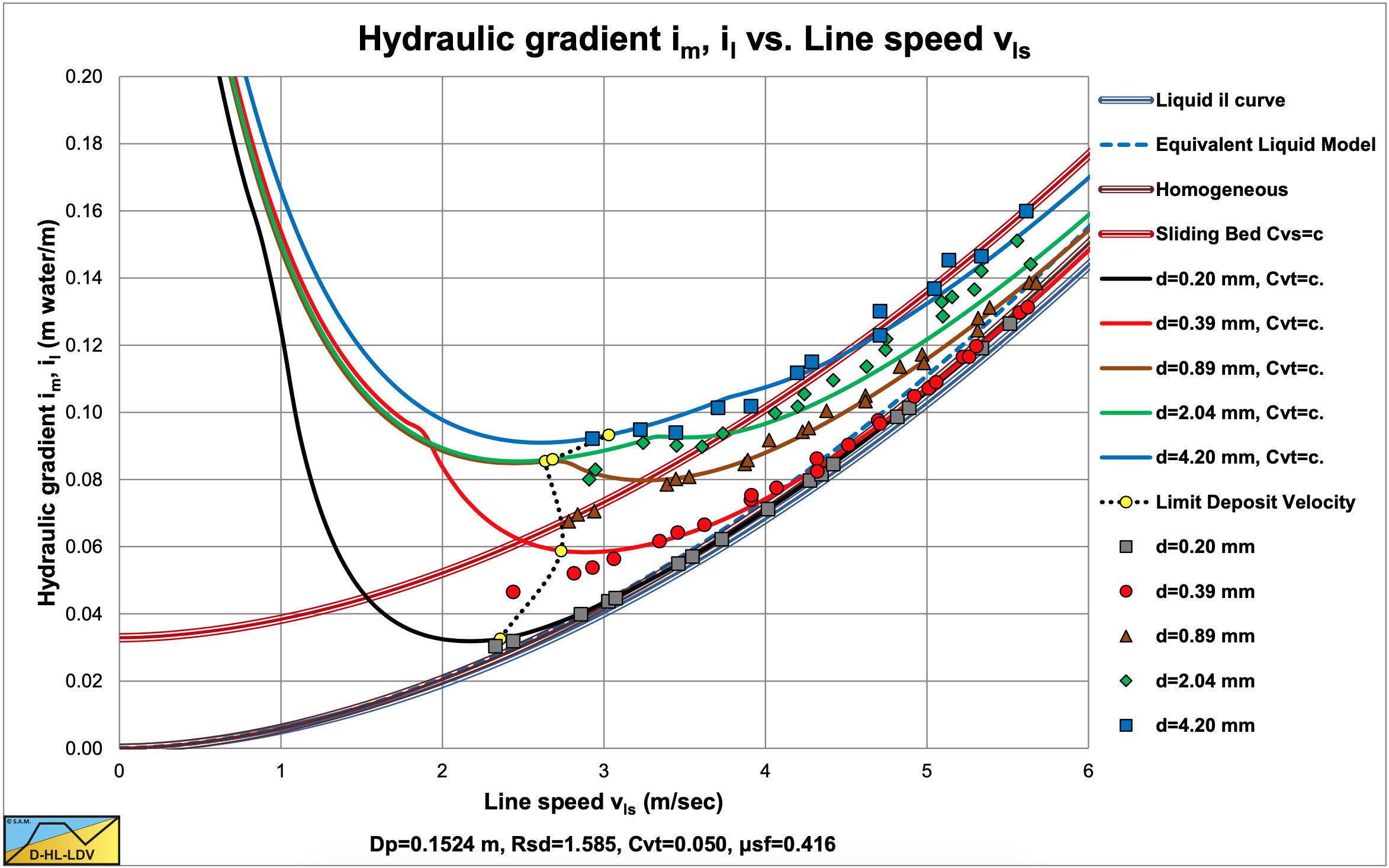
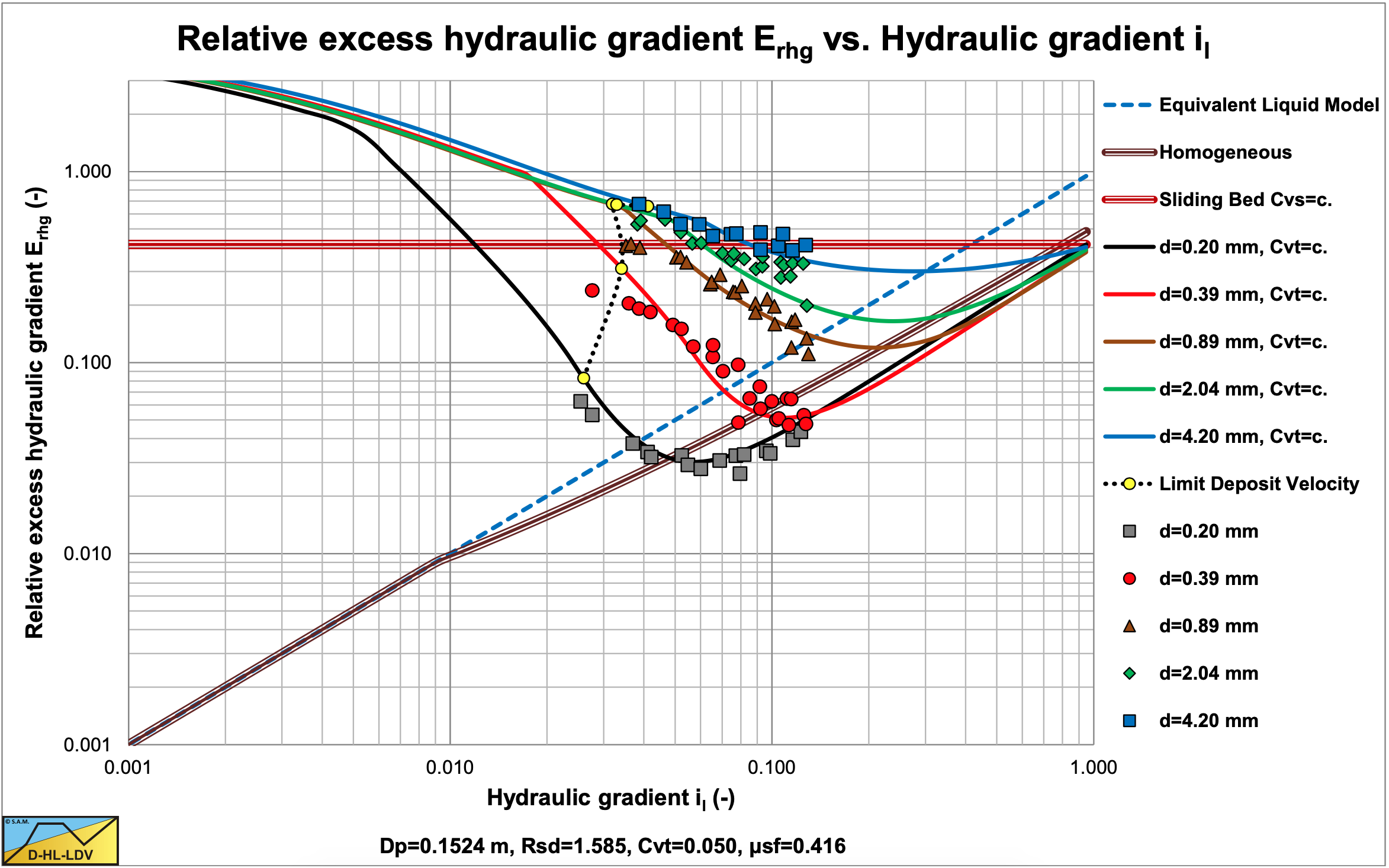
The third new dimensionless number as introduced here. It is the Lắng number La. Lắng is Vietnamese for sediment and this number represents the capability of the slurry flow to form a bed, the sedimentation capability, either fixed or sliding.
\[\ \mathrm{L}_{\mathrm{a}}=\frac{\mathrm{v}_{\mathrm{t}} \cdot\left(\mathrm{1}-\mathrm{C}_{\mathrm{v}} / \mathrm{\kappa}_{\mathrm{C}}\right)^{\beta}}{\mathrm{v}_{\mathrm{ls}}}\]
This gives for the hydraulic gradient:
\[\ \mathrm{i}_{\mathrm{m}}=\mathrm{i}_{\mathrm{l}} \cdot\left(1+\frac{\left(2 \cdot \mathrm{g} \cdot \mathrm{R}_{\mathrm{sd}} \cdot \mathrm{D}_{\mathrm{p}}\right)}{\lambda_{\mathrm{l}}} \cdot \mathrm{C}_{\mathrm{v s}} \cdot \frac{\mathrm{1}}{\mathrm{v}_{\mathrm{l s}}^{2}} \cdot\left(\mathrm{L a}+\frac{\mathrm{8 .5}^{2}}{\mathrm{8}} \cdot \mathrm{C t}^{2} \cdot \mathrm{T h}_{\mathrm{fv}}^{2}\right)\right)\]
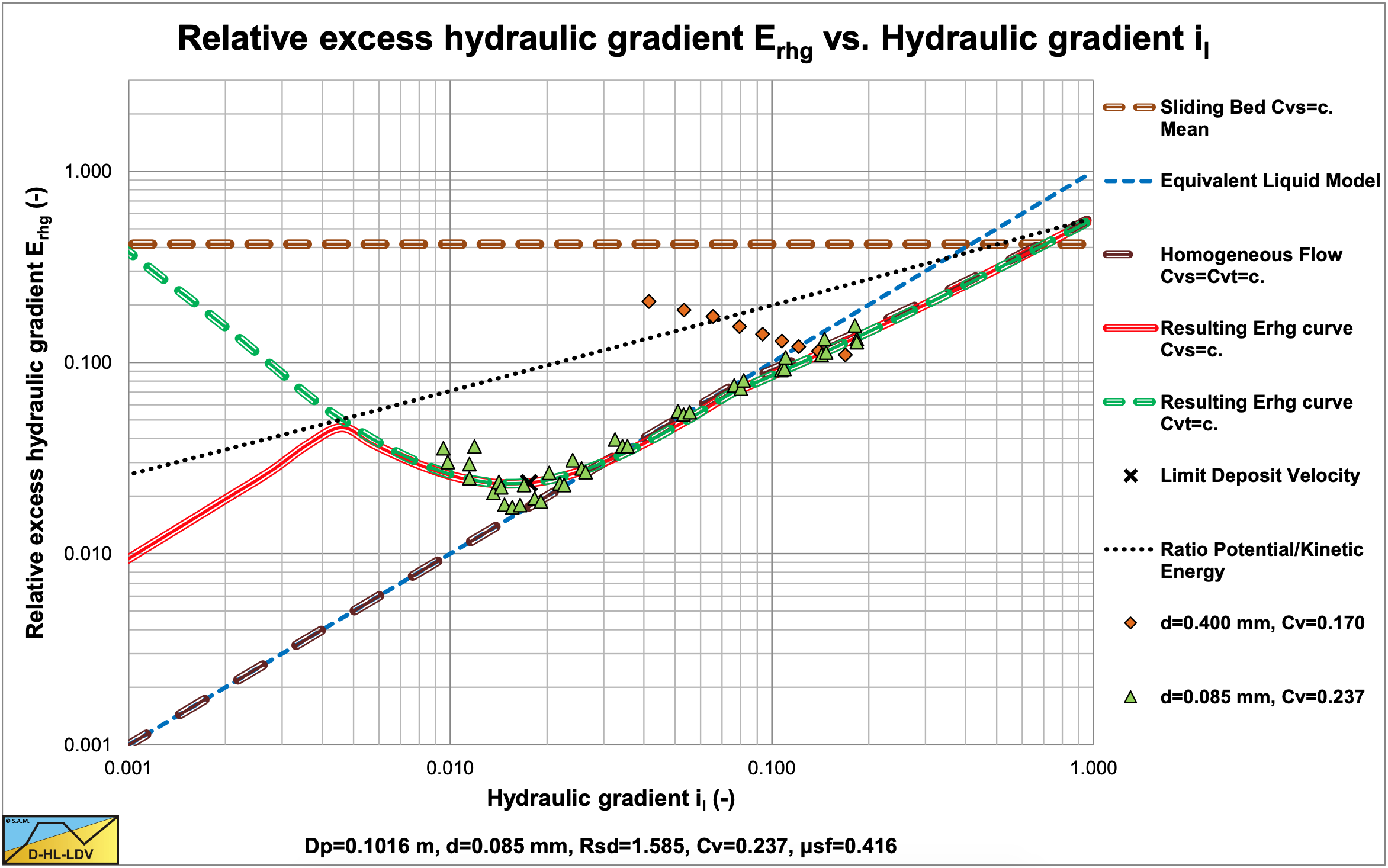
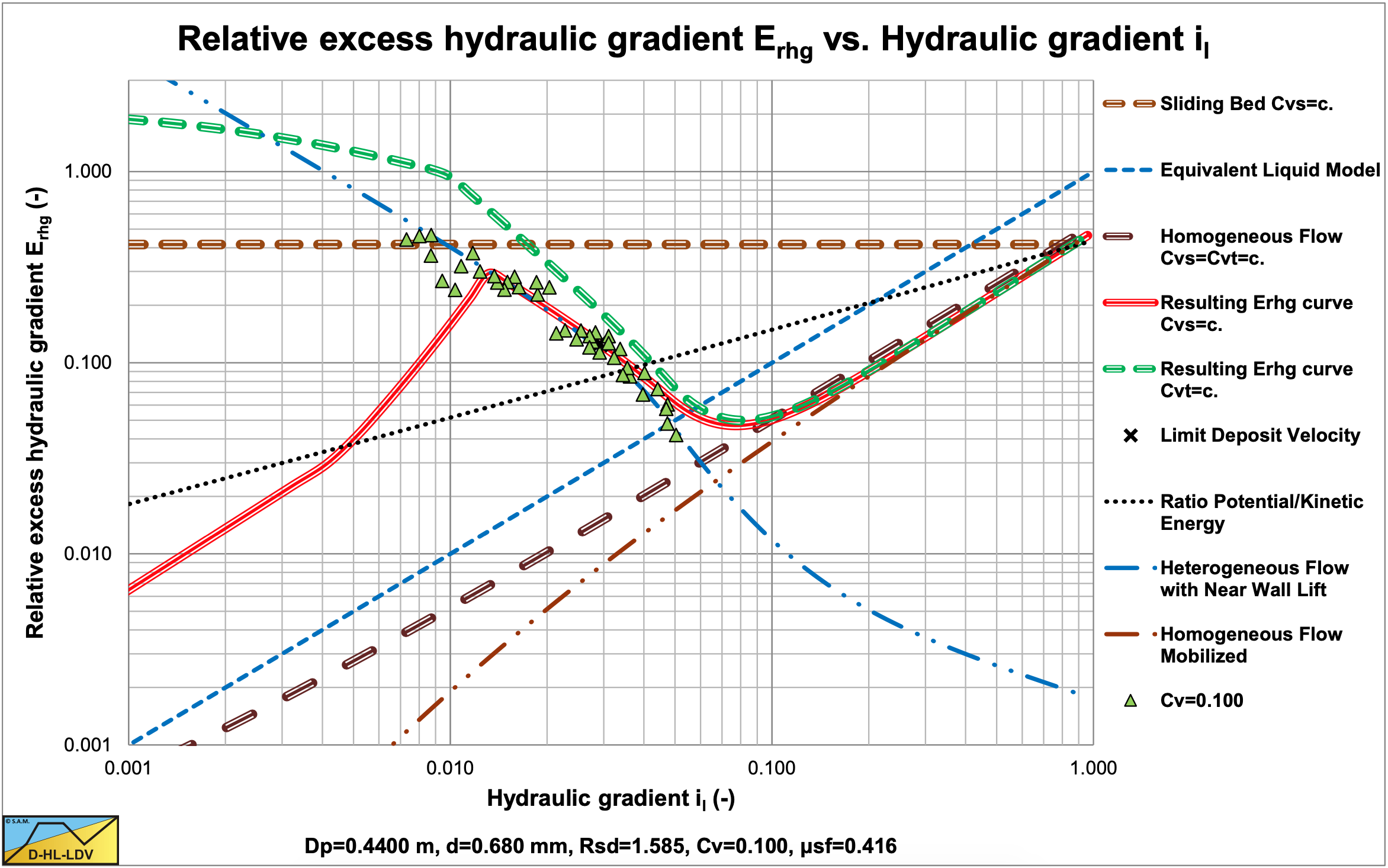
7.5.8 Nomenclature Heterogeneous Regime
|
Ap |
Cross section of a pipe with diameter Dp |
m2 |
|
As |
Cross section of a solid particle with diameter d |
m2 |
|
c |
Proportionality constant |
- |
|
CD |
Particle drag coefficient |
- |
|
Cv |
Volumetric concentration |
- |
|
Cvs |
Volumetric spatial concentration |
- |
|
Cvs,max |
Volumetric spatial concentration where maximum LDV occurs |
- |
|
Cvt |
Volumetric transport/delivered concentration |
- |
|
Cx |
Inverse particle Froude number squared according to Durand & Condolios Frp-2 |
- |
|
d |
Particle diameter |
m |
|
d50 |
Particle diameter at which 50% by weight is smaller |
m |
|
Dp |
Pipe diameter |
m |
|
Erhg |
Relative excess hydraulic gradient |
- |
|
ΔEs,kin,p |
Energy loss of 1 particle at interaction |
N·m |
|
ΔEs,kin,tot |
Energy loss of all particles |
N·m |
|
ΔEs,pot |
Average potential energy of 1 particle |
N·m |
|
ΔEs,pot,tot |
Total potential energy of n particles |
N·m |
|
FD |
Drag force on a particle |
N |
|
FD,tot |
Drag force on all particles |
N |
|
Frp |
Particle Froude number |
- |
|
g |
Gravitational constant 9.81·m/s2 |
m/s2 |
|
i |
Hydraulic gradient |
m/m |
|
im |
Hydraulic gradient mixture |
m/m |
|
iw,il |
Hydraulic gradient water/liquid |
m/m |
|
is,pot |
Hydraulic gradient due to potential energy losses of particles |
m/m |
|
is,kin |
Hydraulic gradient due to kinetic energy losses of particles |
m/m |
|
L, ΔL |
Length of the pipeline |
- |
|
m |
Mass of 1 particle |
kg |
|
n |
Number of particles in a pipe with length ΔL |
- |
|
Δp |
Head loss over a pipeline length ΔL |
kPa |
|
Δpl |
Head loss of liquid over a pipeline length ΔL |
kPa |
|
Δpm |
Head loss of mixture over a pipeline length ΔL |
kPa |
|
Δpm,min |
Head loss of mixture over a pipeline length ΔL where minimum occurs |
kPa |
|
Δps,pot |
Pressure required to compensate for potential energy losses |
kPa |
|
ΔPs,kin |
Power required to compensate for kinetic energy losses |
kW |
|
ΔPs,pot |
Power required to compensate for potential energy losses |
kW |
|
Ql |
Volume flow of liquid/water |
m3/s |
|
Qm |
Volume flow of mixture |
m3/s |
|
Qp |
Volume flow of particles |
m3/s |
|
Re |
Reynolds number |
- |
|
Rep |
Particle Reynolds number |
- |
|
Rsd |
Relative submerged density |
- |
|
s |
Distance |
m |
|
Shr |
Settling velocity Hindered Relative |
- |
|
Srs |
Slip ratio squared/Stratification ratio solids/Friction coefficient (see also μsf) |
- |
|
Δt |
Time interval |
s |
|
vls |
Line speed |
m/s |
|
vls,min |
Line speed where minimum pressure occurs |
m/s |
|
vp |
Particle velocity in direction of average flow |
m/s |
|
vsl |
Slip velocity |
m/s |
|
vt |
Terminal settling velocity of particles |
m/s |
|
u* |
Friction velocity |
m/s |
|
αk |
Factor for kinetic energy losses (fine particles) |
- |
|
αm |
Factor for momentum energy losses (large particles) |
- |
|
αt |
Factor for transition energy losses (medium particles) |
- |
|
α1 |
Power of viscous sub-layer thickness to particle diameter ratio |
- |
|
α2 |
Power of angle of attack |
- |
|
α3 |
Power of relative submerged density to drag coefficient ratio |
- |
|
β |
Power of Richardson & Zaki equation |
- |
|
βk |
Factor for kinetic energy losses (fine particles) |
- |
|
βm |
Factor for momentum energy losses (large particles) |
- |
|
βt |
Factor for transition energy losses (medium particles) |
- |
|
δv |
Thickness viscous sub-layer |
m |
|
ρl |
Liquid density |
ton/m3 |
|
ρw |
Density of water |
ton/m3 |
|
ρs |
Density of solids |
ton/m3 |
|
ρq |
Density of quarts (2.65 ton/m3) |
ton/m3 |
|
λl |
Darcy-Weisbach friction factor |
- |
|
κC |
Concentration eccentricity coefficient |
- |
|
μ |
Friction coefficient for sliding bed (see also Srs) |
- |
|
Φ |
Durand relative excess pressure coefficient |
- |
|
Ω |
Excess pressure factor |
(m/s)3 |
|
ψ |
Durand abscissa |
- |
| \(\ v_{\mathrm{W}}, v_{\mathrm{l}}\) |
Kinematic viscosity of water/liquid |
m2/s |
| \(\ v_{\mathrm{m}}\) |
Kinematic viscosity of mixture with Thomas equation |
m2/s |
| \(\ v_{\mathrm{r}}\) |
Relative kinematic viscosity \(\ v_{\mathrm{m}} / v_{\mathrm{l}}\) |
- |
|
ζ |
Shape factor |
- |
|
Ct |
Cát number, collision impact |
- |
|
La |
Lắng number, sedimentation capability |
- |
|
Th |
Thủy number, collision intensity |
- |


