7.12: The Bed Height
- Page ID
- 32133
7.12.1 Concentration Transformation Equations
For a certain control volume the volumetric transport concentration can be determined if the volumetric spatial concentration and the slip velocity are known, given a certain line speed.
\[\ \mathrm{C_{v t}=\left(1-\frac{v_{s l}}{v_{l s}}\right) \cdot C_{v s}=(1-\xi) \cdot C_{v s}}\]
With the slip ratio:
\[\ \xi=\frac{\mathrm{v}_{\mathrm{sl}} \mid}{\mathrm{v}_{\mathrm{ls}}}\]
Likewise, for a certain control volume, the volumetric spatial concentration can be determined if the volumetric transport concentration and the slip velocity are known, given a certain line speed.
\[\ \mathrm{C}_{\mathrm{v s}}=\left(\frac{\mathrm{v}_{\mathrm{l s}}}{\mathrm{v}_{\mathrm{l s}}-\mathrm{v}_{\mathrm{s l}}}\right) \cdot \mathrm{C}_{\mathrm{v t}}=\left(\frac{\mathrm{1}}{\mathrm{1 - \xi}}\right) \cdot \mathrm{C}_{\mathrm{v t}}\]
These two equations will be used a lot in the following derivations and are considered to be well known.
7.12.2 Fixed Bed
Continuum Equations
Considering a fixed bed, two phases are present, the fixed bed phase and the suspension phase. All the particles that transfer the head losses by inter-particle interactions are considered to be part of the fixed bed phase. All the particles that transfer their head loss contribution through turbulent dispersion are considered to be in the suspension phase. The flow of sediment can be expressed in terms of the pipe cross section times the volumetric spatial concentration times the line speed minus the slip velocity, where the slip velocity is considered to be the average over the whole pipe cross section. Since a fixed bed is considered, this has to be equal to the amount of solids transported in the suspension phase, which is the cross section of the suspension phase times the volumetric transport concentration of this suspension phase times the line speed.
The volume flow of solids is (with a fixed bed the bed velocity is zero):
\[\ \mathrm{Q}_{\mathrm{s}}=\mathrm{A}_{\mathrm{p}} \cdot \mathrm{C}_{\mathrm{v t}} \cdot \mathrm{v}_{\mathrm{l s}}=\mathrm{A}_{\mathrm{p}} \cdot \mathrm{C}_{\mathrm{v s}} \cdot\left(\mathrm{v}_{\mathrm{l s}}-\mathrm{v}_{\mathrm{s l}}\right)=\mathrm{A}_{\mathrm{b}} \cdot \mathrm{C}_{\mathrm{v b}} \cdot \mathrm{v}_{\mathrm{b}}+\mathrm{A}_{\mathrm{s}} \cdot \mathrm{C}_{\mathrm{v t}, \mathrm{s}} \cdot \mathrm{v}_{\mathrm{s}}\]
The total volume flow, liquid plus solids, is:
\[\ \mathrm{Q}_{\mathrm{v}}=\mathrm{A}_{\mathrm{p}} \cdot \mathrm{v}_{\mathrm{l} \mathrm{s}}=\mathrm{A}_{\mathrm{b}} \cdot \mathrm{v}_{\mathrm{b}}+\mathrm{A}_{\mathrm{s}} \cdot \mathrm{v}_{\mathrm{s}}\]
The volume of solids in a pipe section with length ΔL is:
\[\ \mathrm{V}_{\mathrm{s}}=\mathrm{A}_{\mathrm{p}} \cdot \mathrm{C}_{\mathrm{v s}} \cdot \Delta \mathrm{L}=\mathrm{A}_{\mathrm{b}} \cdot \mathrm{C}_{\mathrm{v b}} \cdot \Delta \mathrm{L}+\mathrm{A}_{\mathrm{s}} \cdot \mathrm{C}_{\mathrm{v s}, \mathrm{s}} \cdot \Delta \mathrm{L}\]
The total pipe cross section is the sum of the suspension cross section and the bed cross section:
\[\ \mathrm{A}_{\mathrm{s}}+\mathrm{A}_{\mathrm{b}}=\mathrm{A}_{\mathrm{p}}\]
Derivation
The fraction of the pipe cross section occupied by solids is the sum of the fraction in the bed and the fraction in suspension:
\[\ \mathrm{A}_{\mathrm{p}} \cdot \mathrm{C}_{\mathrm{v s}}=\mathrm{A}_{\mathrm{b}} \cdot \mathrm{C}_{\mathrm{v b}}+\left(\mathrm{A}_{\mathrm{p}}-\mathrm{A}_{\mathrm{b}}\right) \cdot \mathrm{C}_{\mathrm{v s , s}}=\mathrm{A}_{\mathrm{p}} \cdot \mathrm{C}_{\mathrm{v t}} \cdot\left(\frac{\mathrm{v}_{\mathrm{l s}}}{\mathrm{v}_{\mathrm{l s}}-\mathrm{v}_{\mathrm{s l}}}\right)=\mathrm{A}_{\mathrm{p}} \cdot\left(\frac{\mathrm{1}}{\mathrm{1 - \xi}}\right) \cdot \mathrm{C}_{\mathrm{v t}}\]
Now suppose that: \(\ \mathrm{C}_{\mathrm{v s}, \mathrm{s}}=\kappa_{\mathrm{ldv}} \cdot \mathrm{C}_{\mathrm{v t}} \quad\text{ with: }\kappa_{\mathrm{ldv}}=\left(\frac{\mathrm{v}_{\mathrm{l s}, \mathrm{ldv}}}{\mathrm{v}_{\mathrm{l s}, \mathrm{ld v}}-\mathrm{v}_{\mathrm{s} \mathrm{l}, \mathrm{ld v}}}\right)=\left(\frac{\mathrm{1}}{\mathrm{1 - \xi}_{\mathrm{ldv}}}\right)\), based on the slip ratio at the Limit Deposit Velocity, this gives:
\[\ \mathrm{A}_{\mathrm{b}} \cdot \mathrm{C}_{\mathrm{v b}}+\left(\mathrm{A}_{\mathrm{p}}-\mathrm{A}_{\mathrm{b}}\right) \cdot \mathrm{\kappa}_{\mathrm{l d v}} \cdot \mathrm{C}_{\mathrm{v t}}=\mathrm{A}_{\mathrm{p}} \cdot \mathrm{C}_{\mathrm{v t}} \cdot\left(\frac{\mathrm{v}_{\mathrm{l s}}}{\mathrm{v}_{\mathrm{l s}}-\mathrm{v}_{\mathrm{s l}}}\right)=\mathrm{A}_{\mathrm{p}} \cdot\left(\frac{\mathrm{1}}{\mathrm{1 - \xi}}\right) \cdot \mathrm{C}_{\mathrm{v t}}\]
This can be written as:
\[\ \mathrm{A}_{\mathrm{b}} \cdot \mathrm{C}_{\mathrm{v b}} \cdot\left(\mathrm{v}_{\mathrm{l} \mathrm{s}}-\mathrm{v}_{\mathrm{s} \mathrm{l}}\right)+\left(\mathrm{A}_{\mathrm{p}}-\mathrm{A}_{\mathrm{b}}\right) \cdot \mathrm{\kappa}_{\mathrm{l d v}} \cdot \mathrm{C}_{\mathrm{v t}} \cdot\left(\mathrm{v}_{\mathrm{l s}}-\mathrm{v}_{\mathrm{s l}}\right)=\mathrm{A}_{\mathrm{p}} \cdot \mathrm{C}_{\mathrm{v} \mathrm{t}} \cdot \mathrm{v}_{\mathrm{ls}}\]
Combining the terms with the bed cross section gives:
\[\ \mathrm{A}_{\mathrm{b}} \cdot\left(\mathrm{C}_{\mathrm{v b}}-\mathrm{\kappa}_{\mathrm{l d v}} \cdot \mathrm{C}_{\mathrm{v t}}\right) \cdot\left(\mathrm{v}_{\mathrm{l s}}-\mathrm{v}_{\mathrm{s l}}\right)+\mathrm{A}_{\mathrm{p}} \cdot \mathrm{\kappa}_{\mathrm{l d v}} \cdot \mathrm{C}_{\mathrm{v t}} \cdot\left(\mathrm{v}_{\mathrm{l s}}-\mathrm{v}_{\mathrm{s l}}\right)=\mathrm{A}_{\mathrm{p}} \cdot \mathrm{C}_{\mathrm{v t}} \cdot \mathrm{v}_{\mathrm{l s}}\]
Moving the terms with the full pipe cross section to the right hand side gives:
\[\ \mathrm{A}_{\mathrm{b}} \cdot\left(\mathrm{C}_{\mathrm{v b}}-\mathrm{\kappa}_{\mathrm{l d v}} \cdot \mathrm{C}_{\mathrm{v t}}\right) \cdot\left(\mathrm{v}_{\mathrm{l s}}-\mathrm{v}_{\mathrm{s l}}\right)=\mathrm{A}_{\mathrm{p}} \cdot\left(1-\mathrm{\kappa}_{\mathrm{l d v}}\right) \cdot \mathrm{C}_{\mathrm{v t}} \cdot \mathrm{v}_{\mathrm{l s}}+\mathrm{A}_{\mathrm{p}} \cdot \mathrm{\kappa}_{\mathrm{l d v}} \cdot \mathrm{C}_{\mathrm{v t}} \cdot \mathrm{v}_{\mathrm{s l}}\]
This results in an equation for the bed fraction:
\[\ \zeta=\hat{\mathrm{A}}_{\mathrm{b}}=\frac{\mathrm{A}_{\mathrm{b}}}{\mathrm{A}_{\mathrm{p}}}=\frac{\left(1-\kappa_{\mathrm{ldv}}\right) \cdot \mathrm{C}_{\mathrm{v} \mathrm{t}} \cdot \mathrm{v}_{\mathrm{l s}}+\mathrm{\kappa}_{\mathrm{ldv}} \cdot \mathrm{C}_{\mathrm{v} \mathrm{t}} \cdot \mathrm{v}_{\mathrm{sl}}}{\left(\mathrm{C}_{\mathrm{v b}}-\mathrm{\kappa}_{\mathrm{ldv}} \cdot \mathrm{C}_{\mathrm{v t}}\right) \cdot\left(\mathrm{v}_{\mathrm{l s}}-\mathrm{v}_{\mathrm{s l}}\right)}\]
This can be written as:
| \[\ \zeta=\hat{\mathrm{A}}_{\mathrm{b}}=\frac{\mathrm{A}_{\mathrm{b}}}{\mathrm{A}_{\mathrm{p}}}=\frac{\left(1-\mathrm{\kappa}_{\mathrm{l} \mathrm{d v}}\right) \cdot \mathrm{C}_{\mathrm{v} \mathrm{t}}+\mathrm{\kappa}_{\mathrm{l} \mathrm{d} \mathrm{v}} \cdot \mathrm{C}_{\mathrm{v} \mathrm{t}} \cdot \xi}{\left(\mathrm{C}_{\mathrm{v b}}-\mathrm{\kappa}_{\mathrm{l} \mathrm{d} \mathrm{v}} \cdot \mathrm{C}_{\mathrm{v t}}\right) \cdot(\mathrm{1}-\xi)}=\frac{\left(1-\mathrm{\kappa}_{\mathrm{l d v}} \cdot(1-\xi)\right) \cdot \mathrm{C}_{\mathrm{v t}}}{\left(\mathrm{C}_{\mathrm{v} \mathrm{b}}-\mathrm{\kappa}_{\mathrm{l d v}} \cdot \mathrm{C}_{\mathrm{v t}}\right) \cdot(1-\xi)}\] |
Because of the choice of κldv, the relative bed fraction is zero at a line speed equal to the Limit Deposit Velocity.
At the LDV this gives a bed fraction:
\[\ \begin{array}{left} \zeta_{\mathrm{ldv}}=\hat{\mathrm{A}}_{\mathrm{b}}=\frac{\mathrm{A}_{\mathrm{b}}}{\mathrm{A}_{\mathrm{p}}}=\frac{\left(1-\mathrm{\kappa}_{\mathrm{l d v}} \cdot\left(1-\xi_{\mathrm{l} \mathrm{d} \mathrm{v}}\right)\right) \cdot \mathrm{C}_{\mathrm{v} \mathrm{t}}}{\left(\mathrm{C}_{\mathrm{v} \mathrm{b}}-\mathrm{\kappa}_{\mathrm{l d v}} \cdot \mathrm{C}_{\mathrm{v t}}\right) \cdot\left(1-\xi_{\mathrm{l d v}}\right)}=\frac{\mathrm{0}}{\left(\mathrm{C}_{\mathrm{v b}}-\mathrm{\kappa}_{\mathrm{l d v}} \cdot \mathrm{C}_{\mathrm{v t}}\right) \cdot\left(1-\xi_{\mathrm{l d v}}\right)}=\mathrm{0}\\
\mathrm{W i t h}: \quad \mathrm{\kappa}_{\mathrm{ldv}}=\frac{1}{\left(1-\xi_{\mathrm{ldv}}\right)}\end{array}\]
This makes sense, since the definition of the LDV is that there is no stationary or sliding bed.
7.12.3 Sliding Bed
Continuum Equations
The volume flow of solids is (with a sliding bed the bed velocity is non-zero):
\[\ \mathrm{Q}_{\mathrm{s}}=\mathrm{A}_{\mathrm{p}} \cdot \mathrm{C}_{\mathrm{v} \mathrm{t}} \cdot \mathrm{v}_{\mathrm{l s}}=\mathrm{A}_{\mathrm{b}} \cdot \mathrm{C}_{\mathrm{v b}} \cdot \mathrm{v}_{\mathrm{b}}+\mathrm{A}_{\mathrm{s}} \cdot \mathrm{C}_{\mathrm{v} \mathrm{t}, \mathrm{s}} \cdot \mathrm{v}_{\mathrm{s}}\]
The total volume flow, liquid plus solids, is:
\[\ \mathrm{Q}_{\mathrm{v}}=\mathrm{A}_{\mathrm{p}} \cdot \mathrm{v}_{\mathrm{l} \mathrm{s}}=\mathrm{A}_{\mathrm{b}} \cdot \mathrm{v}_{\mathrm{b}}+\mathrm{A}_{\mathrm{s}} \cdot \mathrm{v}_{\mathrm{s}}\]
The volume of solids in a pipe section per unit of length is:
\[\ \mathrm{V}_{\mathrm{s}}=\mathrm{A}_{\mathrm{p}} \cdot \mathrm{C}_{\mathrm{v s}} \cdot \Delta \mathrm{L}=\mathrm{A}_{\mathrm{b}} \cdot \mathrm{C}_{\mathrm{v b}} \cdot \Delta \mathrm{L}+\mathrm{A}_{\mathrm{s}} \cdot \mathrm{C}_{\mathrm{v s}, \mathrm{s}} \cdot \Delta \mathrm{L}\]
The total pipe cross section is the sum of the suspension cross section and the bed cross section:
\[\ \mathrm{A}_{\mathrm{s}}+\mathrm{A}_{\mathrm{b}}=\mathrm{A}_{\mathrm{p}}\]
Derivation
The volume of solids in a pipe section per unit of length can be expressed in terms of the delivered volumetric concentrations, assuming the delivered volumetric concentration in the suspension phase is equal to this concentration at the LDV times a factor α, by:
\[\ \mathrm{V}_{\mathrm{s}}=\mathrm{A}_{\mathrm{p}} \cdot \mathrm{C}_{\mathrm{v s}} \cdot \Delta \mathrm{L}=\mathrm{A}_{\mathrm{p}} \cdot\left(\frac{\mathrm{1}}{\mathrm{1 - \xi}}\right) \cdot \mathrm{C}_{\mathrm{v t}} \cdot \Delta \mathrm{L}=\mathrm{A}_{\mathrm{b}} \cdot \mathrm{C}_{\mathrm{v b}} \cdot \Delta \mathrm{L}+\mathrm{A}_{\mathrm{s}}\left(\frac{\mathrm{\alpha}}{\mathrm{1 - \xi _ { \mathrm { ldv } }}}\right) \cdot \mathrm{C}_{\mathrm{v t}} \cdot \Delta \mathrm{L}\]
Replacing the suspension cross section by the pipe cross section minus the bed cross section gives:
\[\ \mathrm{V}_{\mathrm{s}}=\mathrm{A}_{\mathrm{p}} \cdot \mathrm{C}_{\mathrm{v s}} \cdot \Delta \mathrm{L}=\mathrm{A}_{\mathrm{p}} \cdot\left(\frac{\mathrm{1}}{\mathrm{1}-\xi}\right) \cdot \mathrm{C}_{\mathrm{v t}} \cdot \Delta \mathrm{L}=\mathrm{A}_{\mathrm{b}} \cdot \mathrm{C}_{\mathrm{v b}} \cdot \Delta \mathrm{L}+\left(\mathrm{A}_{\mathrm{p}}-\mathrm{A}_{\mathrm{b}}\right) \cdot\left(\frac{\alpha}{\mathrm{1 - \xi}_{\mathrm{l d v}}}\right) \cdot \mathrm{C}_{\mathrm{v t}} \cdot \Delta \mathrm{L}\]
Moving all terms with the pipe cross section to the left hand side and all terms with the bed cross section to the right hand side, gives:
\[\ \mathrm{A_{p} \cdot\left(\frac{1}{1-\xi}-\frac{\alpha}{1-\xi_{l d v}}\right) \cdot C_{v t}=A_{b} \cdot\left(C_{v b}-\frac{\alpha \cdot C_{v t}}{1-\xi_{l d v}}\right)}\]
This gives for the bed fraction:
| \[\ \zeta=\hat{\mathrm{A}}_{\mathrm{b}}=\frac{\mathrm{A}_{\mathrm{b}}}{\mathrm{A}_{\mathrm{p}}}=\frac{\left(1-\alpha \cdot \kappa_{\mathrm{l} \mathrm{d} \mathrm{v}} \cdot(1-\xi)\right) \cdot \mathrm{C}_{\mathrm{v} \mathrm{t}}}{\left(\mathrm{C}_{\mathrm{v} \mathrm{b}}-\frac{\alpha \cdot \mathrm{C}_{\mathrm{v} \mathrm{t}}}{1-\xi_{\mathrm{ldv}}}\right)}=\frac{\left(1-\alpha \cdot \mathrm{\kappa}_{\mathrm{l} \mathrm{d} \mathrm{v}} \cdot(1-\xi)\right) \cdot \mathrm{C}_{\mathrm{v} \mathrm{t}}}{\left(\mathrm{C}_{\mathrm{v} \mathrm{b}}-\alpha \cdot \mathrm{\kappa}_{\mathrm{l} \mathrm{d} \mathrm{v}} \cdot \mathrm{C}_{\mathrm{v} \mathrm{t}}\right) \cdot(1-\xi)}\] |
When α=1 this gives the same result as the fixed bed approach. At the LDV this only gives a bed height of zero and a bed height of 100% if α=1. A value of α>1 will give a higher bed fraction, A value of α<1 will give a lower bed fraction. So α could be a function of the line speed with a value of 1 at both zero line speed and at the LDV.
The examples in this book are made with α=1, so with a fixed bed approach.
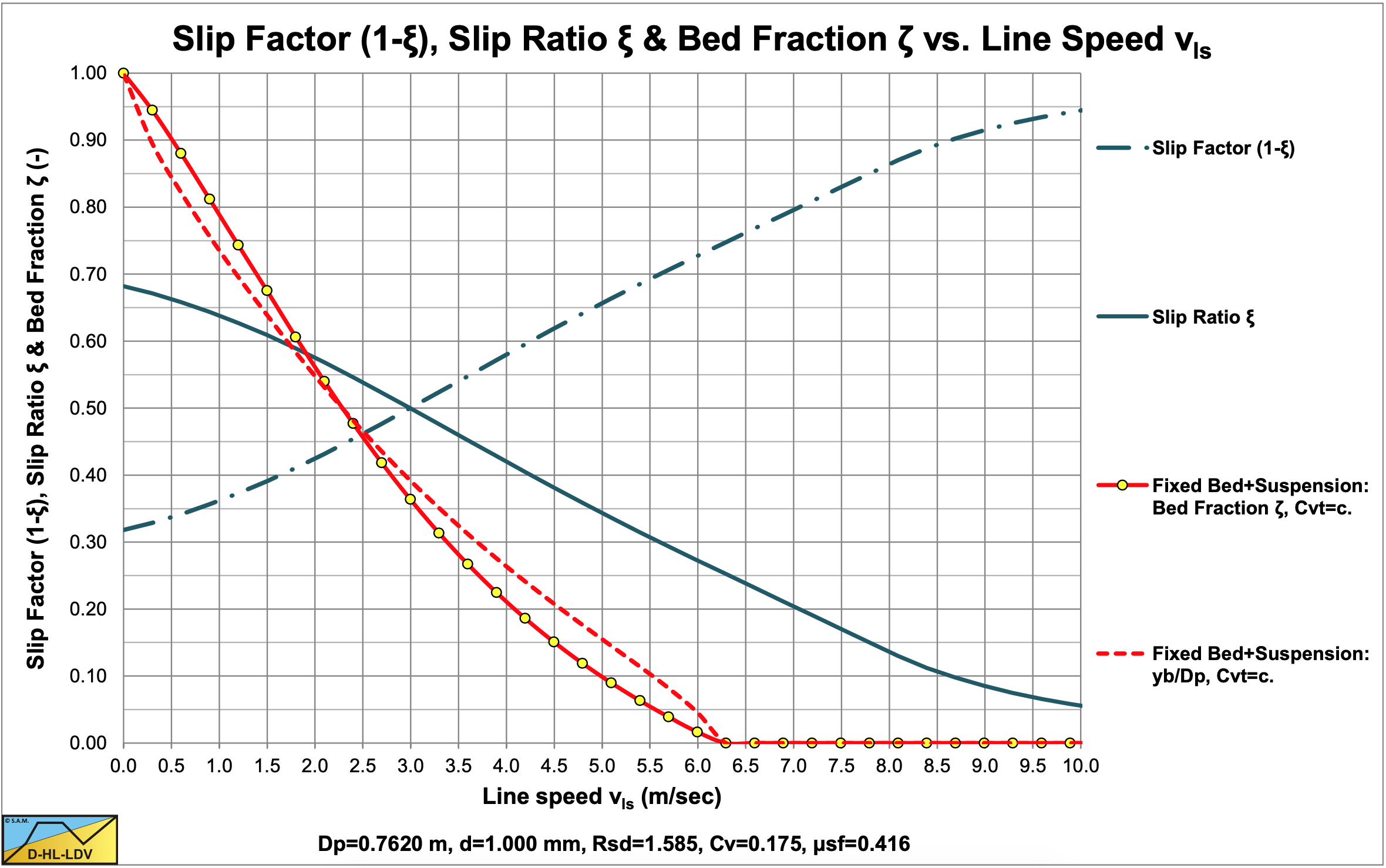
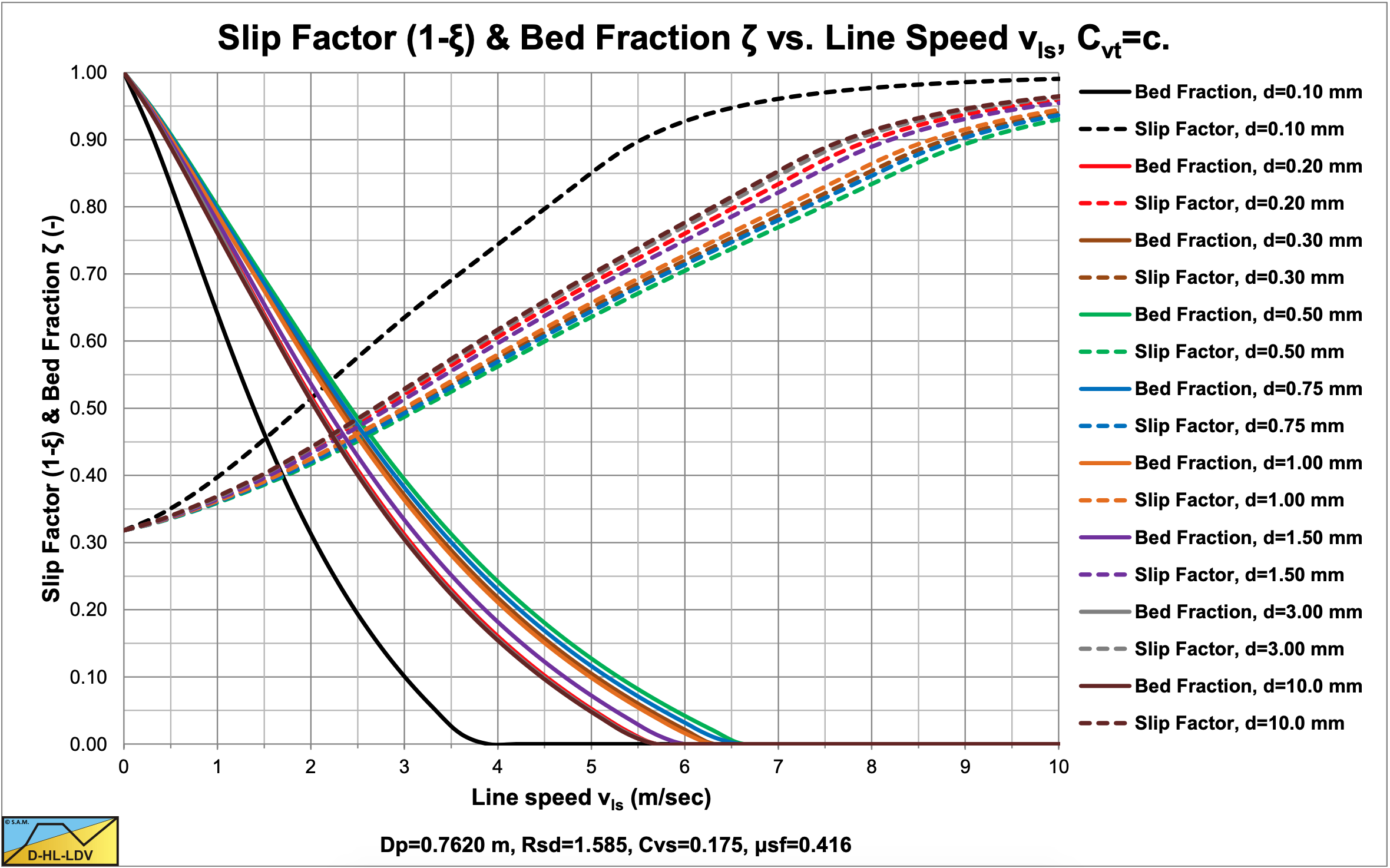
7.12.4 Some Results
Based on the real slip velocity, the spatial concentration and the transport concentration can be converted into each other, giving the possibility to determine the spatial concentration eat each line speed, given a certain constant transport concentration. This also makes it possible to determine the fraction of the bed occupying the pipe cross section assuming a fixed bed, which is very valuable for dredging companies. Below the Limit Deposit Velocity, the bed fraction increases slowly with decreasing line speed. At a certain line speed however, the bed fraction will increase more rapidly with further decreasing line speed. Maybe the definition of the Limit Deposit Velocity should be reconsidered. Now the definition is the line speed at which a bed disappears completely with increasing line speed or appears with decreasing line speed. A definition based on an acceptable fraction of the bed occupying the pipe cross section would be more appropriate. Accepting a bed fraction of 10% would reduce the Limit Deposit Velocity from, in the example in Figure 7.12-1 and Figure 7.12-2, 6.25 m/sec to about 5 m/sec for the d=1 mm particles.
The graphs shown are based on the fixed bed equation, so the bed height curves may differ slightly for a sliding bed.
7.12.5 Nomenclature Bed Height
|
Ab |
Bed cross section |
m2 |
|
Ap |
Pipe cross section |
m2 |
|
As |
Suspension cross section (cross section above the bed) |
m2 |
| \(\ \tilde{\mathrm{A}}_{\mathrm{b}}\) |
Bed fraction |
- |
|
Cvt |
Delivered (transport) volumetric concentration |
- |
|
Cvt,s |
Delivered (transport) volumetric concentration in suspended layer |
- |
|
Cvs |
Spatial volumetric concentration |
- |
|
Cvs,s |
Spatial volumetric concentration in suspended layer |
- |
|
Cvb |
Spatial volumetric concentration bed (1-n) |
- |
|
d |
Particle diameter |
m |
|
Dp |
Pipe diameter |
m |
|
ΔL |
Pipe length |
m |
|
n |
Porosity |
- |
|
Qs |
Total solids flow |
m3/s |
|
Qv |
Total flow, liquid + solids |
m3/s |
|
Rsd |
Relative submerged density |
- |
|
vls |
Line speed |
m/s |
|
vb |
Bed velocity |
m/s |
|
vs |
Suspension velocity |
m/s |
|
vls,ldv |
Limit Deposit Velocity |
m/s |
|
vsl |
Slip velocity |
m/s |
|
vsl,ldv |
Slip velocity at the LDV |
m/s |
|
Vs |
Volume of solids in a pipe section |
m3 |
|
α |
Slip ratio factor |
- |
|
κldv |
Reversed slip ratio at LDV |
- |
|
μsf |
Sliding friction factor |
- |
|
ξ |
Slip ratio |
- |
|
ξldv |
Slip ratio at LDV |
- |
|
ζ |
Bed fraction |
- |
|
ζldv |
Bed fraction at the LDV |
- |


