Skip to main content
Engineering LibreTexts

8.14: The Concentration Distribution

  1. Last updated
  2. Save as PDF
  • Page ID
    32295

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    The fraction can be determined by the angle β matching a certain vertical coordinate, similar to the angle β for the stationary and sliding bed.

    \[\ \beta=\operatorname{acos}\left(\frac{0.5-\frac{\mathrm{r}}{\mathrm{D_{p}}}}{0.5}\right) \Leftrightarrow \frac{\mathrm{r}}{\mathrm{D_{p}}}=\frac{1-\cos (\beta)}{2}\]

    The fraction f is now:

    \[\ \mathrm{f}=\frac{\beta-\sin (\beta) \cdot \cos (\beta)}{\pi}\]

    The concentration distribution is (without or with hindered settling):

    \[\ \mathrm{C}_{\mathrm{v s}}(\mathrm{f})=\mathrm{C}_{\mathrm{v B}} \cdot \mathrm{e}^{-\frac{\alpha_{\mathrm{sm}}}{\mathrm{C}_{\mathrm{vr}}} \cdot\left(\frac{\mathrm{v}_{\mathrm{ls}, \mathrm{l} \mathrm{d v}}}{\mathrm{v}_{\mathrm{ls}}}\right)^{0.925} \cdot \frac{\mathrm{v}_{\mathrm{tv}}}{\mathrm{v}_{\mathrm{tv}, \mathrm{ld v}}} \cdot \mathrm{f}}{\quad \text{or}\quad} \mathrm{C}_{\mathrm{v s}}(\mathrm{f})=\mathrm{C}_{\mathrm{v B}} \cdot \mathrm{e}^{-\frac{\alpha_{\mathrm{sm}}}{\mathrm{C}_{\mathrm{vr}}} \cdot\left(\frac{\mathrm{v}_{\mathrm{ls}, \mathrm{ld v}}}{\mathrm{v}_{\mathrm{ls}}}\right)^{0.925} \cdot \frac{\mathrm{v}_{\mathrm{thv}}}{\mathrm{v}_{\mathrm{th v,ldv}}}\cdot\mathrm{f}}\]

    The correction factor appears to depend only on the relative concentration Cvr accordoing to:

    \[\ \alpha_{\mathrm{sm}}=0.9847+0.304 \cdot \mathrm{C}_{\mathrm{vr}}-1.196 \cdot \mathrm{C}_{\mathrm{vr}}^{2}-0.5564 \cdot \mathrm{C}_{\mathrm{vr}}^{3}+0.47 \cdot \mathrm{C}_{\mathrm{vr}}^{4}\]

    The bottom concentration is now (without or with hindered settling):

    \[\ \mathrm{C_{vB}=C_{vb}\cdot \frac{\left(\alpha_{sm}\cdot \left(\frac{v_{ls,ldv}}{v_{ls}} \right)^{0.925}\cdot \frac{v_{tv}}{v_{tv,ldv}} \right)}{\left(1-e^{\frac{\alpha_{sm}}{C_{vr}}\cdot \left(\frac{v_{ls,ldv}}{v_{ls}} \right)^{0.925}\cdot \frac{v_{tv}}{v_{tv,ldv}}}\right)}\text{ or }C_{vB}=C_{vb}\cdot\frac{\left(\alpha_{sm}\cdot\left(\frac{v_{ls,ldv}}{v_{ls}} \right)^{0.925}\cdot \frac{v_{thv}}{v_{thv,ldv}} \right)}{\left(1-e^{-\frac{\alpha_{sm}}{C_{vr}}\cdot \left(\frac{v_{ls,ldv}}{v_{ls}} \right)^{0.925}\cdot \frac{v_{thv}}{v_{thv,ldv}}} \right)}} \]

    If the bottom concentration is higher than the bed concentration, the concentration profile has to be adjusted. If it is assumed that the settling velocity in the suspension hardly changes as a function of the line speed, the equation for the concentration distribution becomes:

    \[\ \mathrm{C}_{\mathrm{v s}, \mathrm{0}}(\mathrm{f})=\mathrm{C}_{\mathrm{v} \mathrm{B}} \cdot \mathrm{e}^{-\frac{\mathrm{\alpha}_{\mathrm{s m}}}{\mathrm{C}_{\mathrm{v r}}} \cdot\left(\frac{\mathrm{v}_{\mathrm{ls}, \mathrm{ld v}}}{\mathrm{v}_{\mathrm{l s}}}\right)^{1.15}\cdot \mathrm{f}}\]

    The bottom concentration is now:

    \[\ \mathrm{C}_{\mathrm{v B}}=\mathrm{C}_{\mathrm{v b}} \cdot \frac{\left(\alpha_{\mathrm{s m}} \cdot\left(\frac{\mathrm{v}_{\mathrm{l s}, \mathrm{ld} \mathrm{v}}}{\mathrm{v}_{\mathrm{l s}}}\right)^{1.15}\right)}{\left(1-\mathrm{e}^{-\frac{\alpha_{\mathrm{sm}}}{\mathrm{C}_{\mathrm{vr}}} \cdot\left(\frac{\mathrm{v}_{\mathrm{ls}, \mathrm{ldv}}}{\mathrm{v}_{\mathrm{ls}}}\right)^{1.15}}\right)}\]

    At each level in the pipe the corrected concentration gradient can be determined for the first iteration step according to:

    \[\ \left(\frac{\mathrm{d} \mathrm{C}_{\mathrm{v s}, \mathrm{1}}(\mathrm{f})}{\mathrm{d r}}\right)=\left(\frac{\mathrm{d} \mathrm{C}_{\mathrm{v s}, \mathrm{0}}(\mathrm{f})}{\mathrm{d r}}\right) \cdot\left(\frac{\left(1-\mathrm{C}_{\mathrm{v r}, 0}\right)}{\left(1-\mathrm{C}_{\mathrm{v r}}\right)}\right)^{\alpha \cdot \frac{\beta}{2.34}}\]

    For the following iteration steps the concentration gradient has to be adjusted according to:

    \[\ \left(\frac{\left.\mathrm{d} \mathrm{C}_{\mathrm{v} \mathrm{s}, \mathrm{i}} \mathrm{(} \mathrm{f}\right)}{\mathrm{d r}}\right)=\left(\frac{\left.\mathrm{d} \mathrm{C}_{\mathrm{v s}, \mathrm{i}-\mathrm{1}} \mathrm{( f}\right)}{\mathrm{d} \mathrm{r}}\right) \cdot\left(\frac{\mathrm{C}_{\mathrm{v r}, \mathrm{i}-\mathrm{1}}(\mathrm{f})}{\mathrm{C}_{\mathrm{v r}, \mathrm{i}-\mathrm{2}}(\mathrm{f})}\right) \cdot\left(\frac{\left(1-\mathrm{C}_{\mathrm{v} \mathrm{r}, \mathrm{i}-1}\right)}{\left(1-\mathrm{C}_{\mathrm{v r}, \mathrm{i}-2}\right)}\right)^{\alpha \cdot \frac{\beta}{2.34}}\]

    Integrating the concentration profile again, starting at the bottom with either the bottom concentration (above the LDV) or the bed concentration (below the LDV), gives a concentration profile adjusted for local hindered settling. The power α is determined with the following equations:

    \[\ \begin{array}{left}\text{SF = Shape Factor} \quad \text{SF=0.77 for sand} \quad \text{SF=1.0 for spheres}\\
    C_{\text {vrMax }}=\frac{0.175}{\mathrm{C_{v b}}}\\
    \alpha=0.275 \cdot\left(\frac{\mathrm{SF}}{0.77}\right)^{1.5} \cdot\left(\frac{\mathrm{C}_{\mathrm{vr}}}{\mathrm{C}_{\mathrm{vrMax}}}\right)^{3} \cdot\left(\frac{\mathrm{v}_{\mathrm{ls}, \mathrm{LDV}}}{\mathrm{v}_{\mathrm{ls}}}\right)^{0.15} \quad \mathrm{C}_{\mathrm{vr}}<\mathrm{C}_{\mathrm{vrMax}}\\
    \alpha=0.275 \cdot\left(\frac{\mathrm{SF}}{0.77}\right)^{1.5} \cdot\left(\frac{\mathrm{C}_{\mathrm{vr}}}{\mathrm{C}_{\mathrm{vrMax}}}\right)^{2 / 3} \cdot\left(\frac{\mathrm{v}_{\mathrm{ls}, \mathrm{LDV}}}{\mathrm{v}_{\mathrm{ls}}}\right)^{0.15} \quad \mathrm{C}_{\mathrm{vr}} \geq \mathrm{C}_{\mathrm{vrMax}}\end{array}\]

    Figure 8.14-1: The concentration profile without local hindered settling (red line) and with local hindered settling (iteration 1-12).

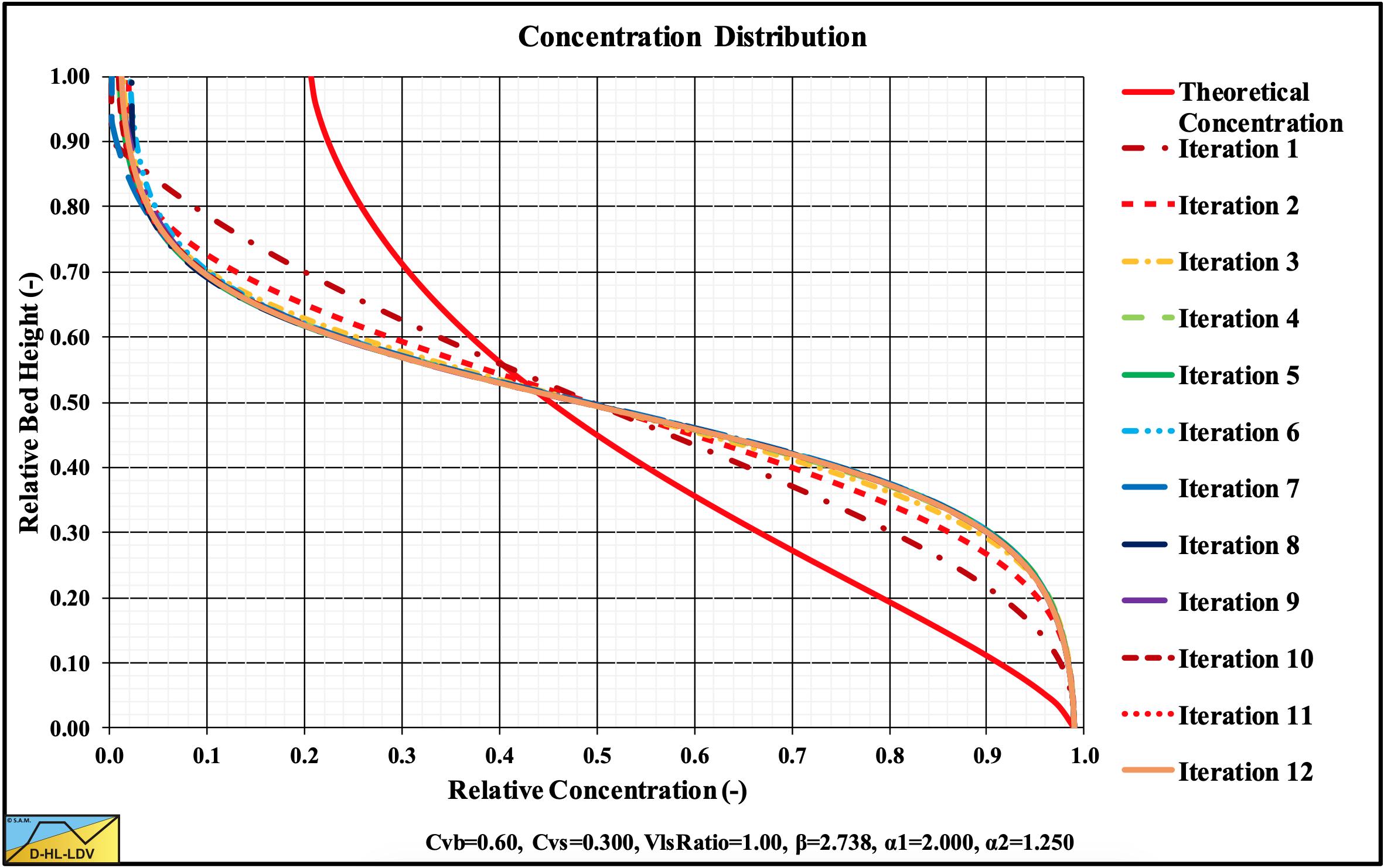
    Screen Shot 2020-08-03 at 10.01.51 AM.png

    Because the Limit Deposit Velocity is based on the occurrence of some bed at the bottom of the pipe, this bed does not need to have the maximum bed density. A bed may start to occur with a bottom concentration of about 50%, while the maximum bed concentration will be in the range of 60%-65%. In order to find a bottom concentration of about 50% at the LDV, an additional velocity ratio rLDV is introduced giving:

    \[\ \mathrm{C_{vB}=C_{vb}\cdot \frac{\left(\alpha_{sm}\cdot\left(r_{LDV}\cdot \frac{v_{s,ldv}}{v_{ls}} \right)^{1.15}\right)}{\left(1-e^{-\frac{\alpha_{sm}}{C_{vr}}\cdot \left(r_{LDV}\cdot\frac{v_{ls,ldv}}{v_{ls}} \right)^{1.15}}\right)} \quad\text{and}\quad C_{vs}(f)=C_{vB}\cdot e^{-\frac{\alpha_{sm}}{C_{vr}}\cdot \left(r_{LDV \cdot \frac{v_{ls,ldv}}{v_{ls}}} \right)^{1.15}\cdot f}}\]

    The additional velocity ratio rLDV can be estimated by:

    \[\ \begin{array}{left}\text{SF = Shape Factor} \quad \text{SF=0.77 for sand} \quad \text{SF=1.0 for spheres}\\
    \mathrm{C_{\text {vrMax }}=\frac{0.175}{C_{v b}}}\\
    \mathrm{\alpha_{\beta}=1.8-56 \cdot v_{t} \quad\text{ with: }\quad \alpha_{\beta} \geq 1.1}\\
    \text{If }\mathrm{C}_{\mathrm{v r}}<\mathrm{C}_{\mathrm{v r} \mathrm{M a x}}\text{ then}\\
    \mathrm{r_{L D V}=0.6 \cdot \frac{e^{(\beta / 2.34)^{\alpha_{\beta}}}}{e} \cdot\left(\frac{0.0005}{d}\right)^{S F^{6}} \cdot\left(\frac{C_{v r M a x}}{C_{v r}}\right)^{1 / 3} \quad\text{ with: }\quad r_{L D V} \geq 1.2 \cdot\left(\frac{C_{v r M a x}}{C_{v r}}\right)^{1 / 3}}\\
    \text{If }\mathrm{C}_{\mathrm{v r}} \geq \mathrm{C}_{\mathrm{v r} \mathrm{M a x}}\text{ then}\\
    \mathrm{r_{L D V}=0.6 \cdot \frac{e^{(\beta / 2.34)^{\alpha_{\beta}}}}{e} \cdot\left(\frac{0.0005}{d}\right)^{S F^{6}} \cdot\left(\frac{C_{v r}}{C_{v r M a x}}\right)^{1 / 6} \quad\text{ with: }\quad r_{L D V} \geq 1.2 \cdot\left(\frac{C_{v r}}{C_{v r M a x}}\right)^{1 / 6}}\end{array}\]

    The factor 1.2 is based on the ratio 60% to 50%, the maximum bed concentration to the minimum bed concentration. For most of the experimental data analysed, a maximum bed concentration of 60% gives very good results. The LDV has a maximum at a concentration of 17.5%.

    This page titled 8.14: The Concentration Distribution is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Sape A. Miedema (TU Delft Open Textbooks) via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.