9.3: The Limit Deposit Velocity
- Page ID
- 32512
9.3.1 Analysis
The Limit Deposit Velocity is defined here as the line speed above which is no stationary bed or sliding bed, Thomas (1962). Below the LDV there may be either a stationary or fixed bed or a sliding bed.
For the critical velocity often the Minimum Hydraulic Gradient Velocity (MHGV) is used, Wilson (1942). For higher concentrations this MHGV may be close to the LDV, but for lower concentrations this is certainly not the case. Yagi et al. (1972) reported using the MHGV, making the data points for the lower concentrations too low, which is clear from Figure 9.3-1. Another weak point of the MHGV is, that it depends strongly on the model used for the heterogeneous flow regime. Durand and Condolios (1952), Fuhrboter (1961), Jufin and Lopatin (1966) and others will each give a different MHGV. In dredging the process is instationary, meaning a constantly changing PSD and concentration in long pipelines, making it almost impossible to determine the MHGV.
Wilson (1979) derived a method for determining the transition velocity between the stationary bed and the sliding bed, which is named here the Limit of Stationary Deposit Velocity (LSDV). Since the transition stationary bed versus sliding bed, the LSDV, will always give a smaller velocity value than the moment of full suspension or saltation, the LDV, one should use the LDV, to be sure there is no deposit at all. For small particles it is also possible that the bed is already completely suspended before the bed could ever start sliding (theoretically). In that case an LSDV does not even exist.
This is the reason for choosing the LDV as the critical velocity, independent of the head loss model and always existing Miedema & Ramsdell (2015A).
The Froude number FL is often used for the LDV, because it allows comparison of the LDV for different pipe diameters Dp and relative submerged densities Rsd without having to change the scale of the graph, this is defined as:
\[\ \mathrm{F}_{\mathrm{L}}=\frac{\mathrm{v}_{\mathrm{l s}, \mathrm{ld} \mathrm{v}}}{\sqrt{\mathrm{2 \cdot g} \cdot \mathrm{R}_{\mathrm{s d}} \cdot \mathrm{D}_{\mathrm{p}}}}\]
It should be noted that sometimes the 2 and sometimes the relative submerged density Rsd are omitted.
Because there are numerous data and equations for the critical velocity (LSDV, LDV or MHGV), some equations based on physics, but most based on curve fitting, a selection is made of the equations and methods from literature. The literature analyzed are from Wilson (1942), Durand and Condolios (1952), Newitt et al. (1955), Jufin and Lopatin (1966), Zandi and Govatos (1967), Charles (1970), Graf et al. (1970), Wilson and Judge (1976), Wasp et al. (1977), Wilson and Judge (1977), Thomas (1979), Oroskar and Turian (1980), Parzonka et al. (1981), Turian et al. (1987), Davies (1987), Schiller and Herbich (1991), Gogus and Kokpinar (1993), Gillies (1993), Berg (1998), Kokpinar and Gogus (2001), Shook et al. (2002), Wasp and Slatter (2004), Sanders et al. (2004), Lahiri (2009), Poloski et al. (2010) and Souza Pinto et al. (2014).
The research consisted of two parts, analyzing the experimental data and analyzing the resulting models based on these data. First the experimental data will be discussed.
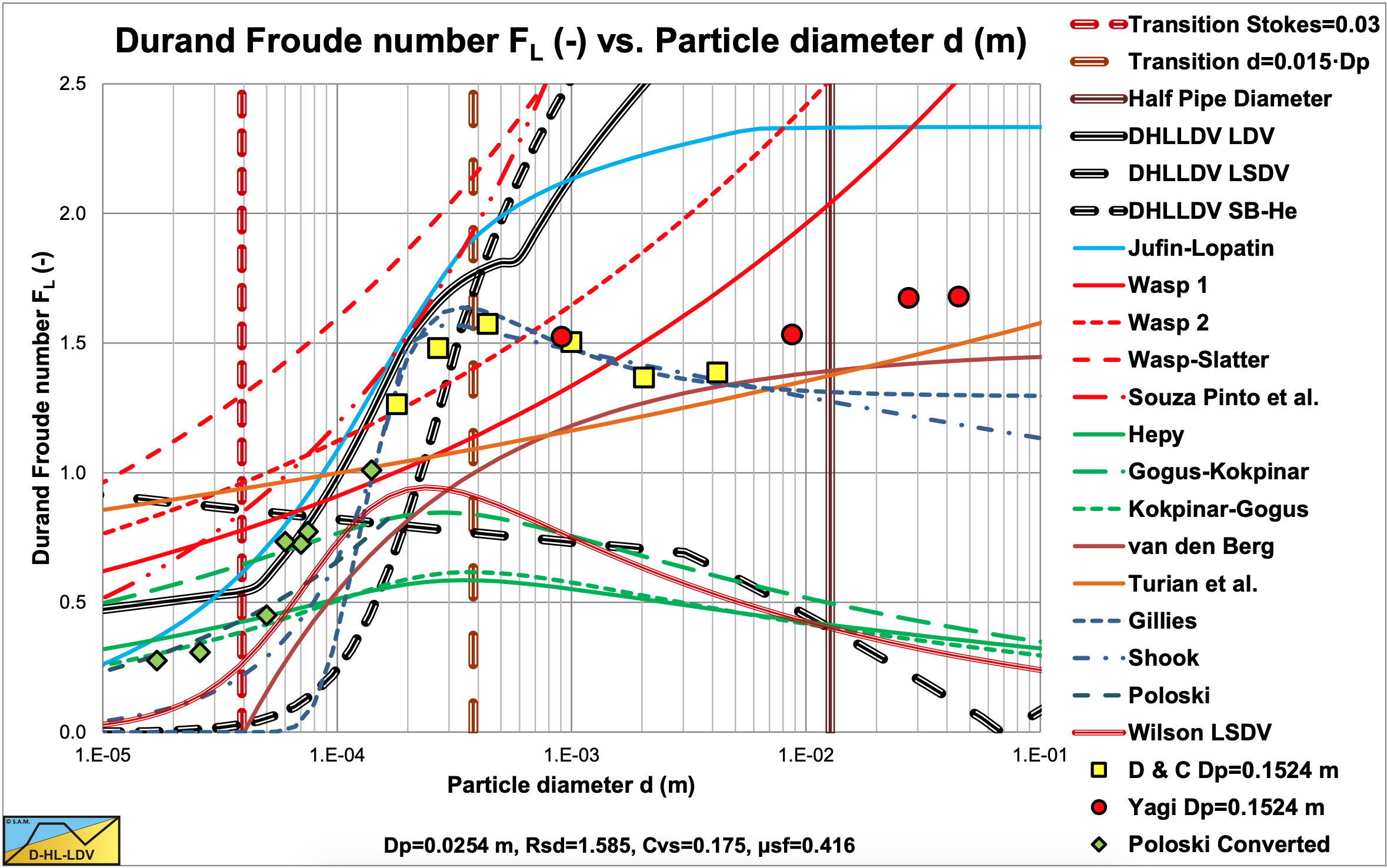
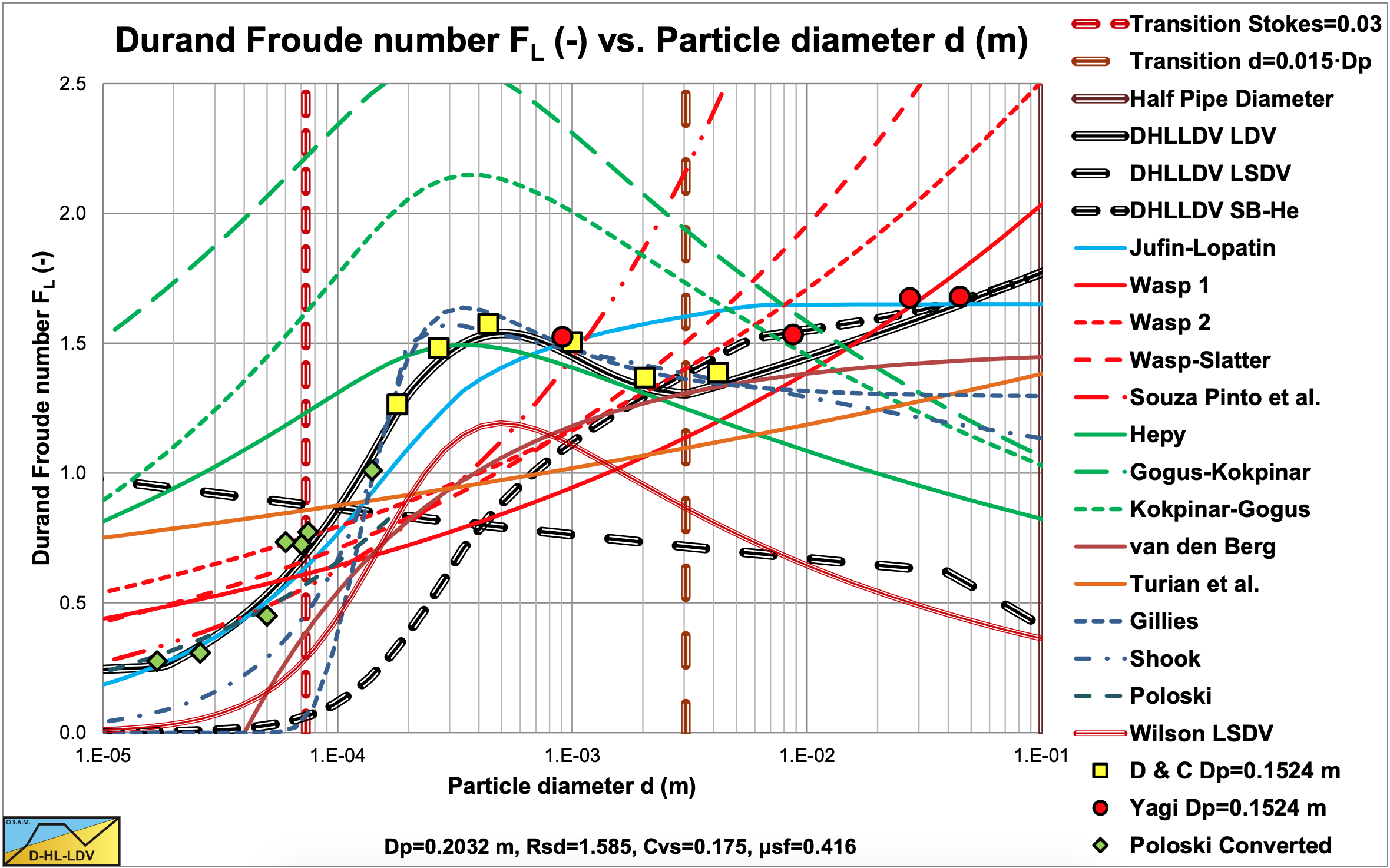
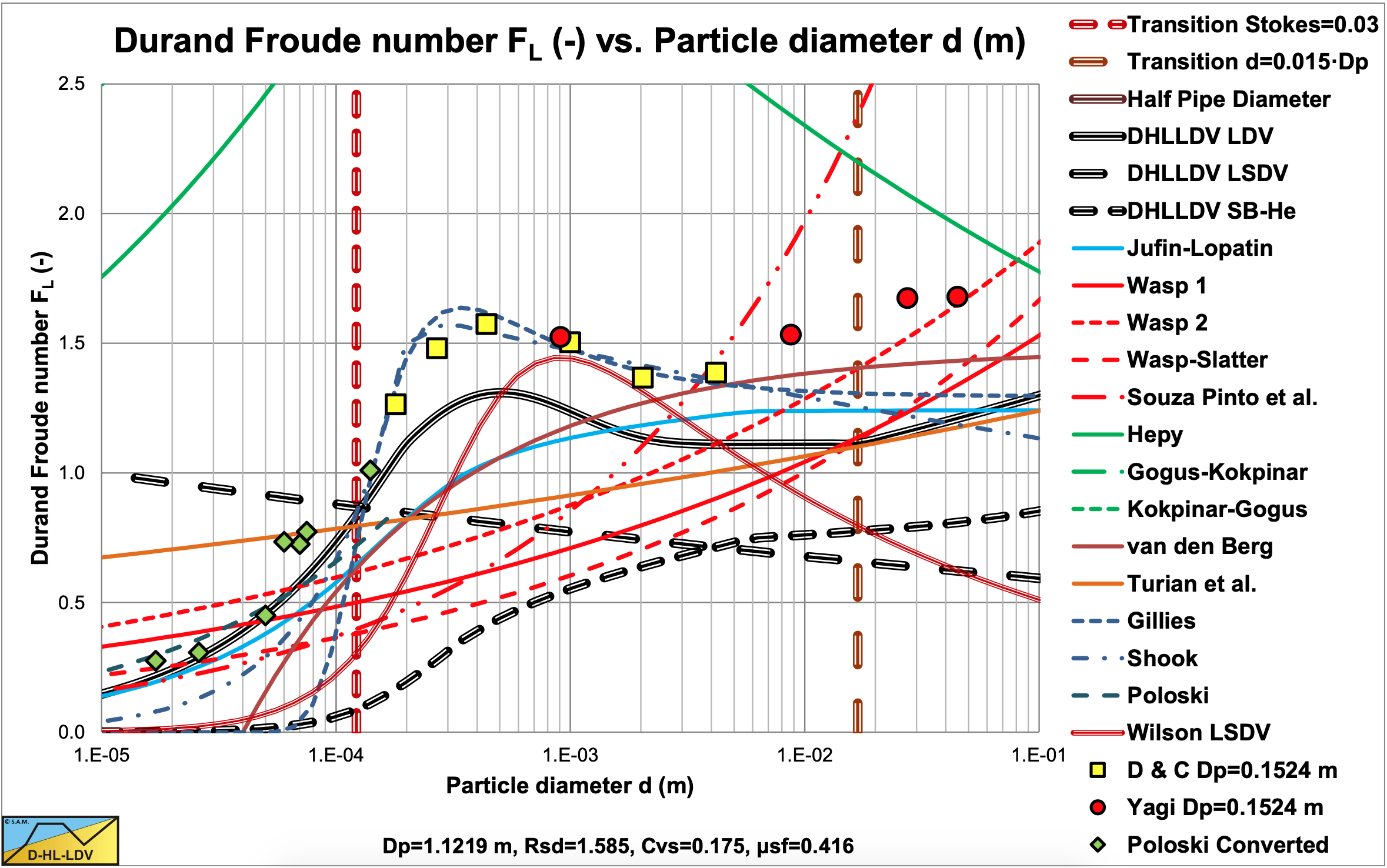
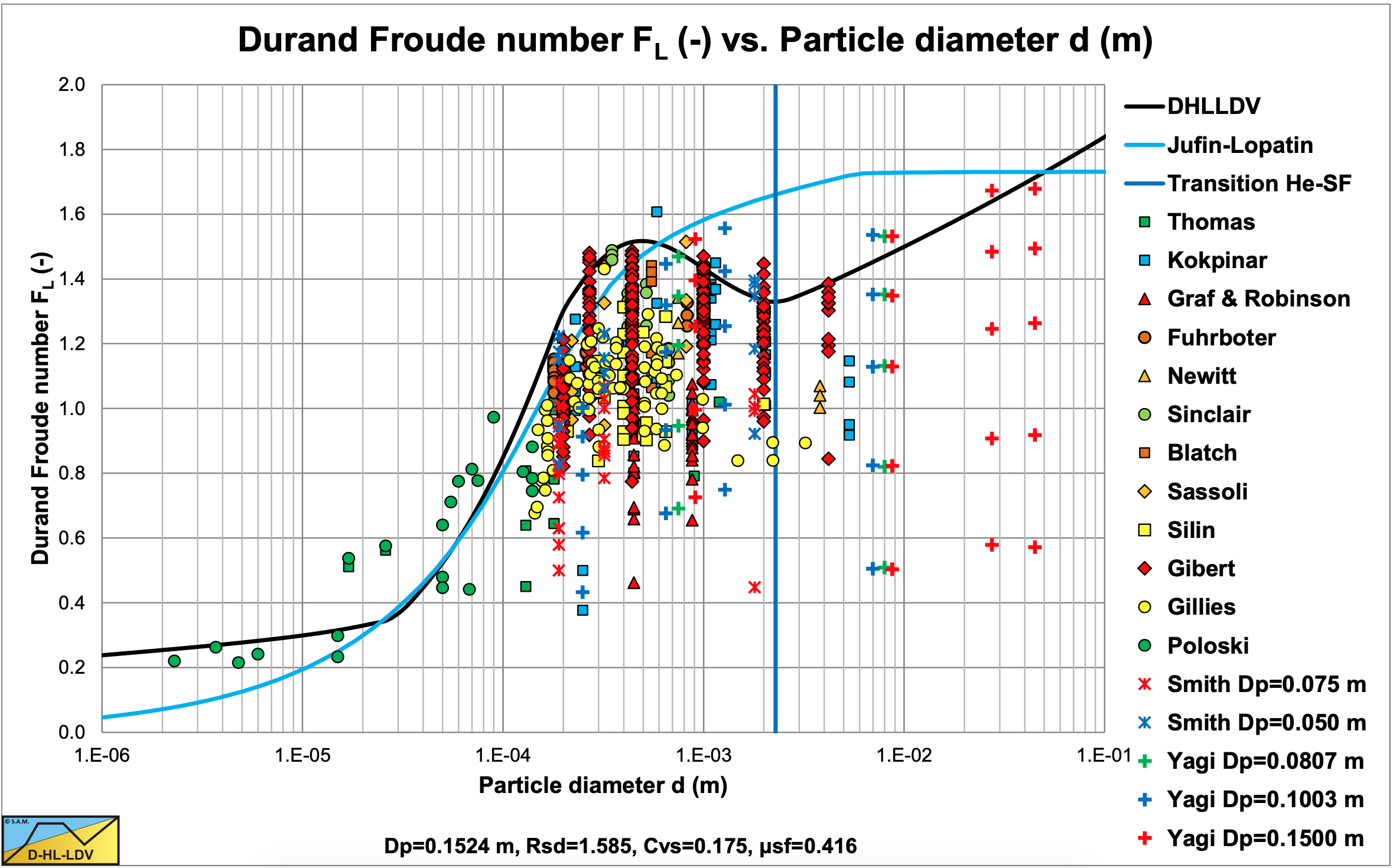
Figure 9.3-1 shows many data points of various authors for sand and gravel in water. Each column of data points shows the results of experiments with different volumetric concentrations, where the highest points were at volumetric concentrations of about 15%–20%, higher concentrations gave lower points. The experimental data also shows that smaller pipe diameters, in general, give higher Durand and Condolios (1952) Froude FL numbers. The two curves in the graph are for the Jufin and Lopatin (1966) equation, which is only valid for sand and gravel, and the DHLLDV Framework which is described by Miedema & Ramsdell (2015A).
Both models give a sort of upper limit to the LDV. The data points of the very small particle diameters, Thomas (1979) and Poloski (2010), were carried out in very small to medium diameter pipes, while the two curves are constructed for a 0.1524 (6 inch) pipe, resulting in slightly lower curves. Data points above the DHLLDV curve are in general for pipe diameters smaller than 0.1524 m. Some special attention is given to the relation between the Durand Froude FL number and the pipe diameter Dp. Both Thomas (1979) and Wasp et al. (1977) carried out research with a d = 0.18 mm particle in 6 pipe diameters. These experiments show a slight decrease of the FL value with increasing pipe diameter with a power close to –0.1, meaning the LDV increases with the pipe diameter to a power close to 0.4 and not to 0.5 as assumed by Durand and Condolios (1952).
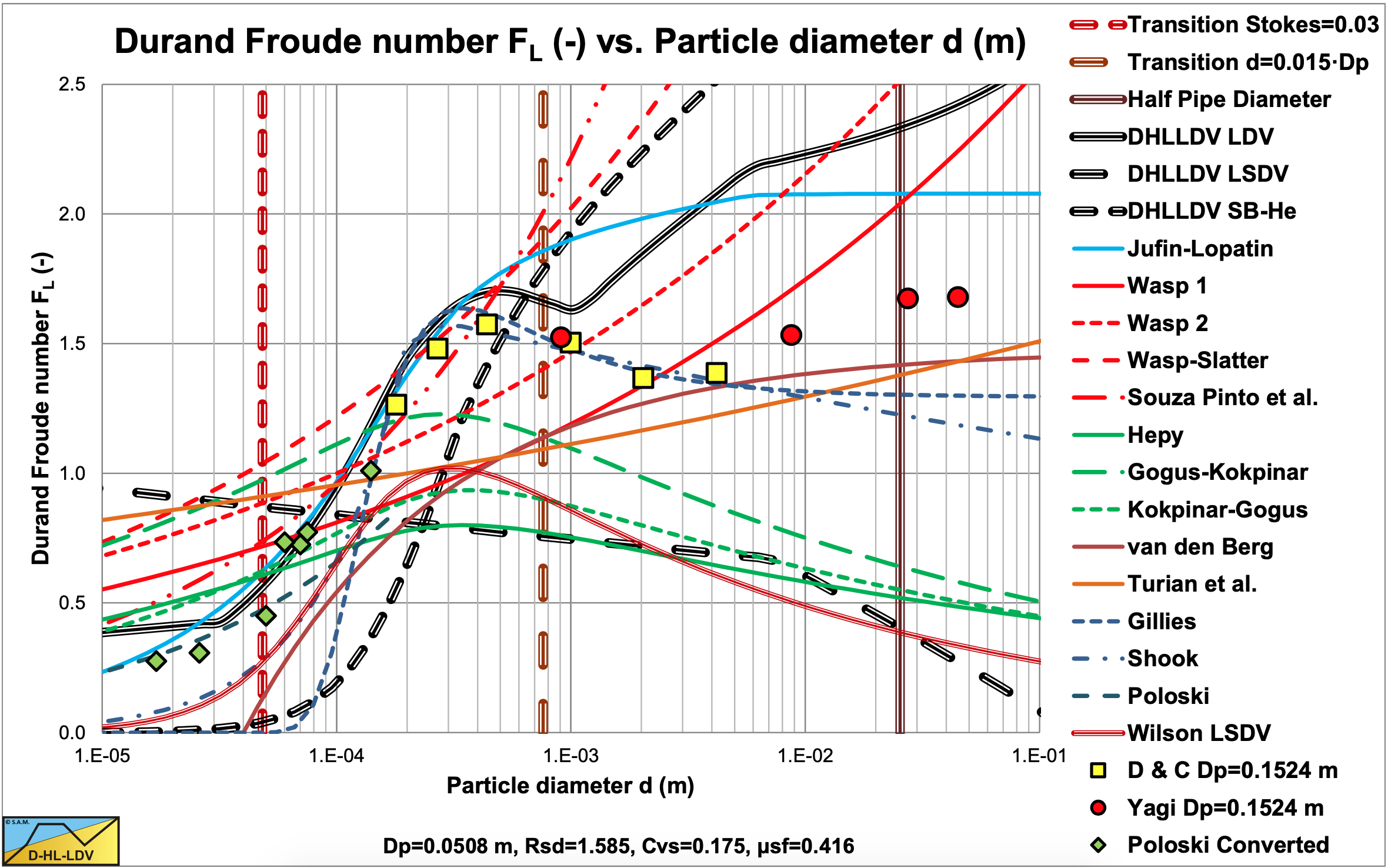
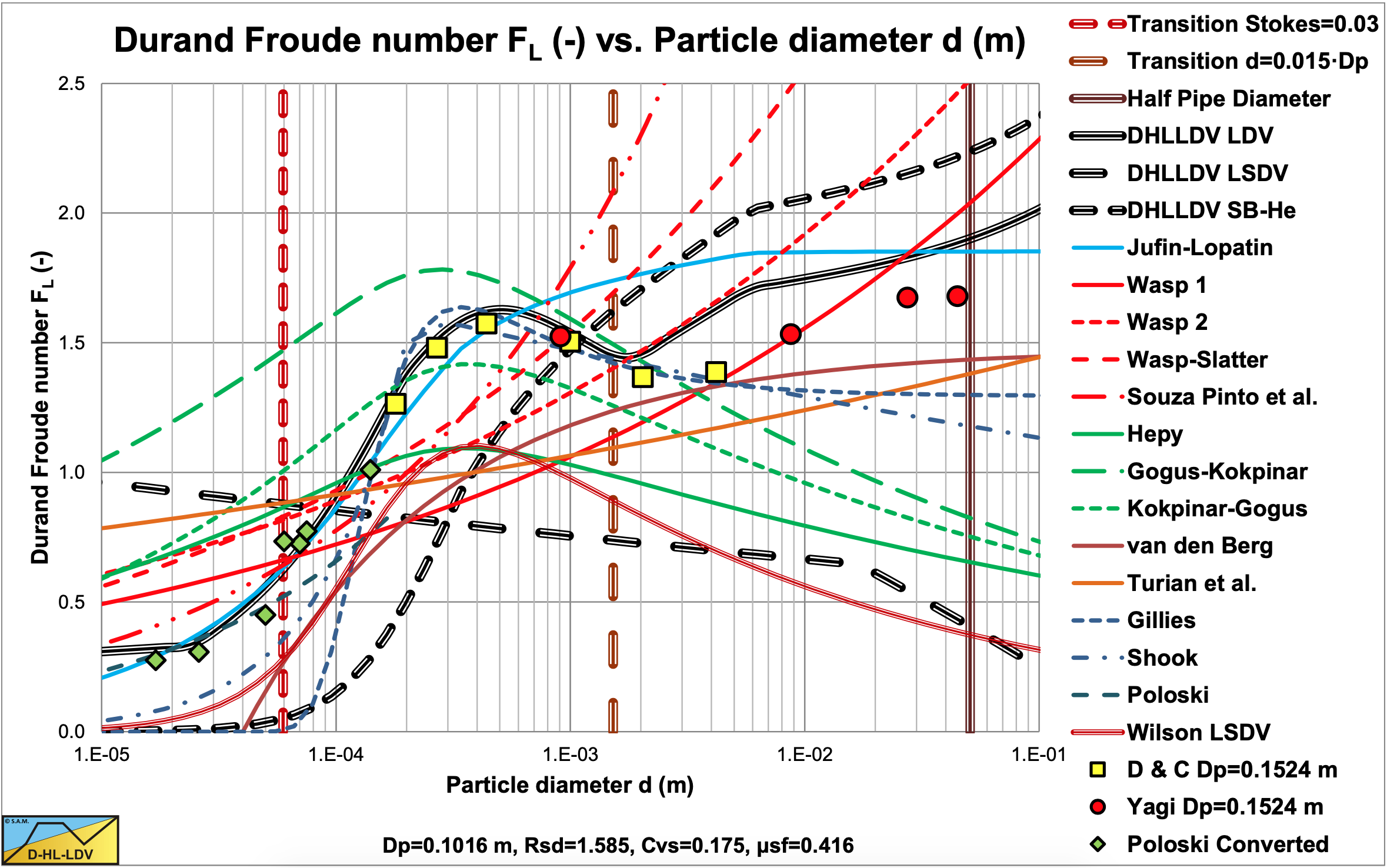
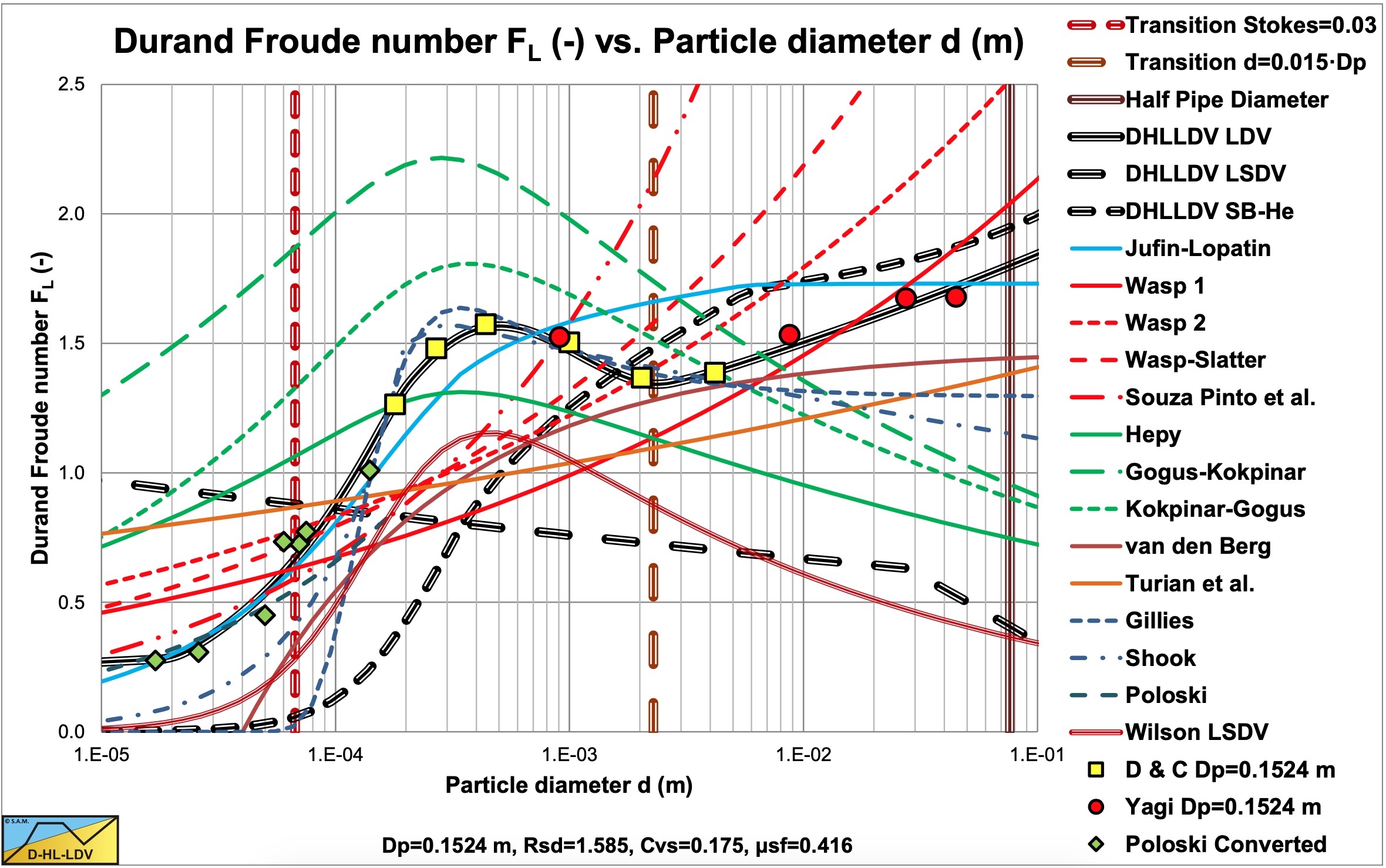
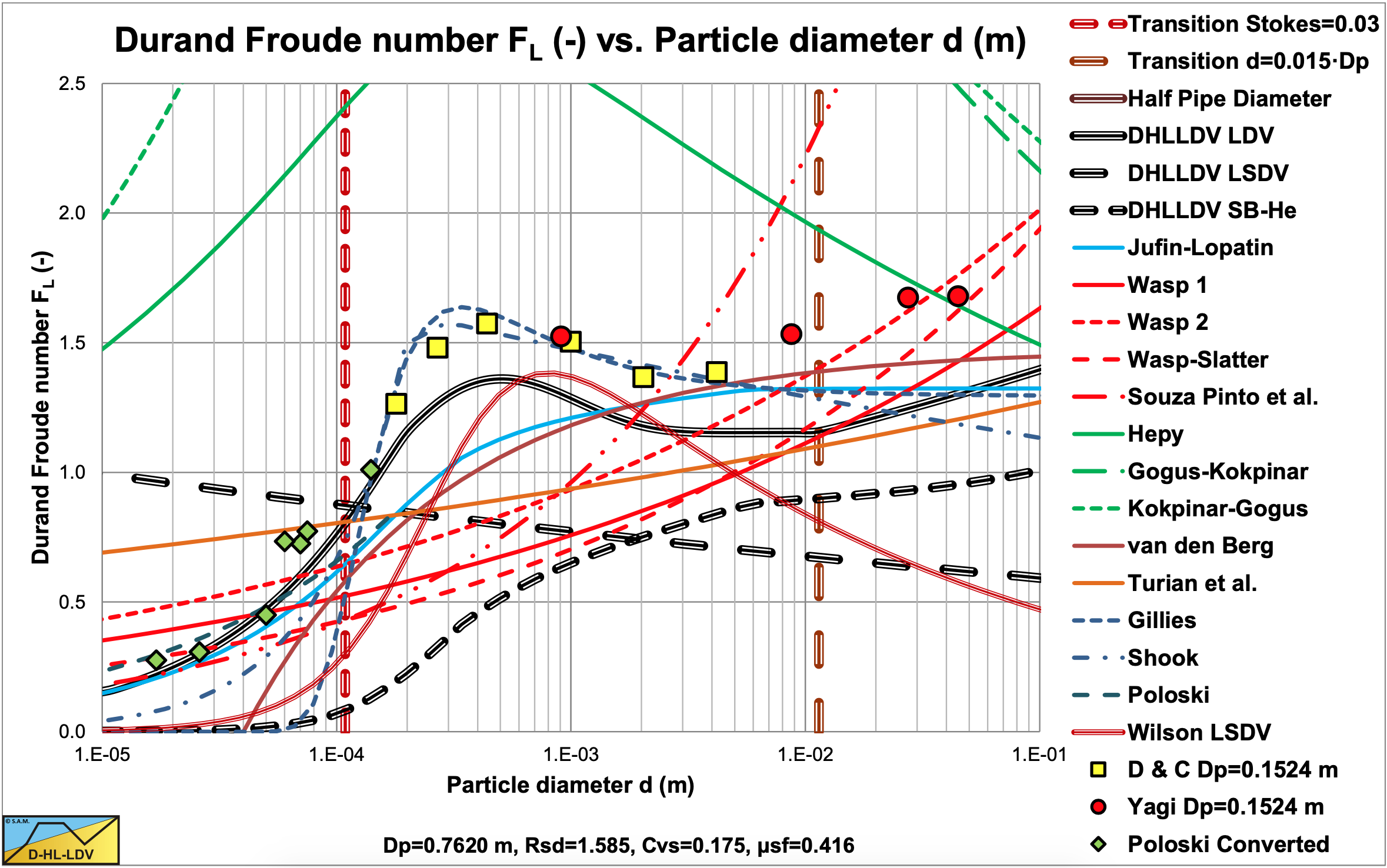
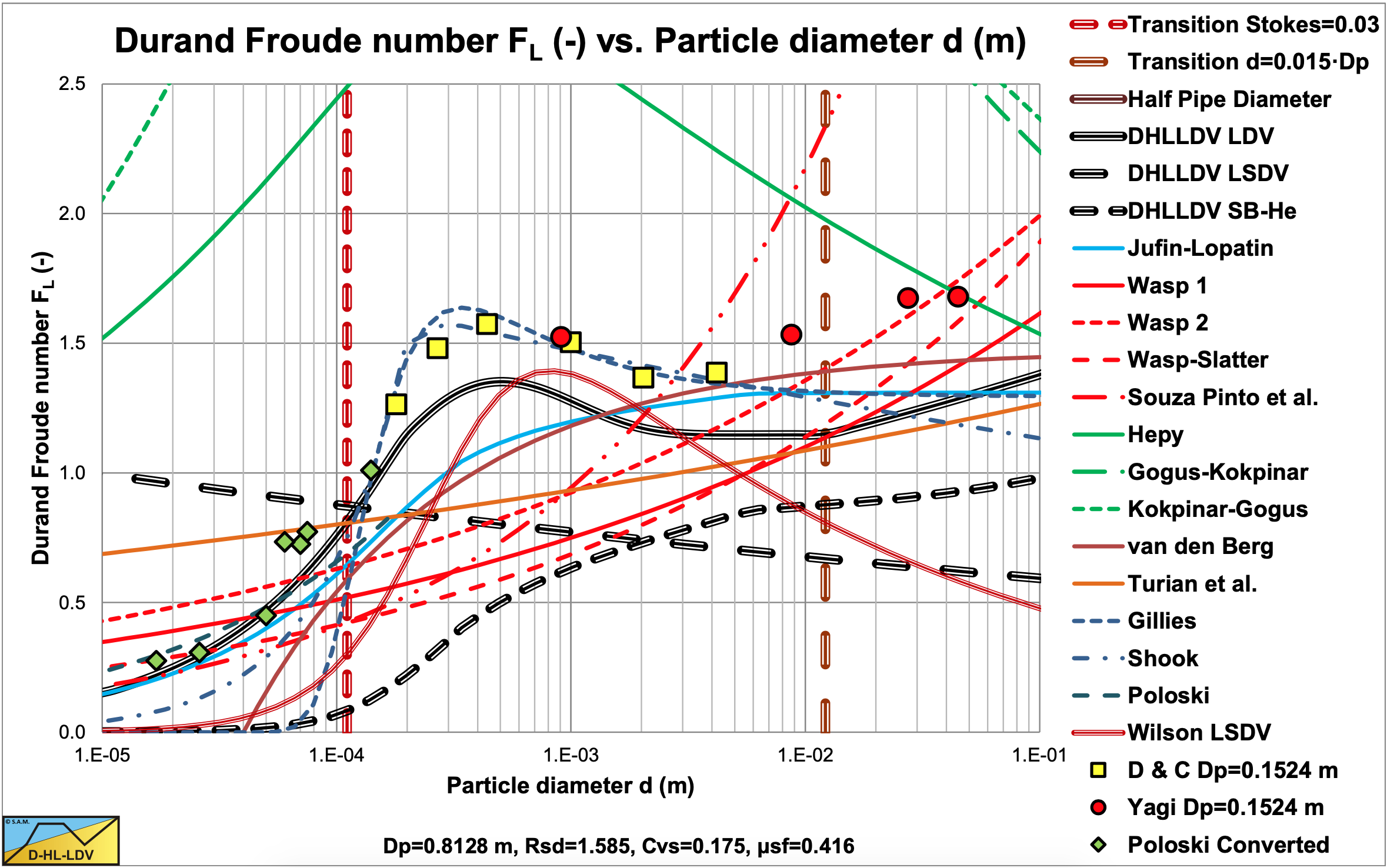
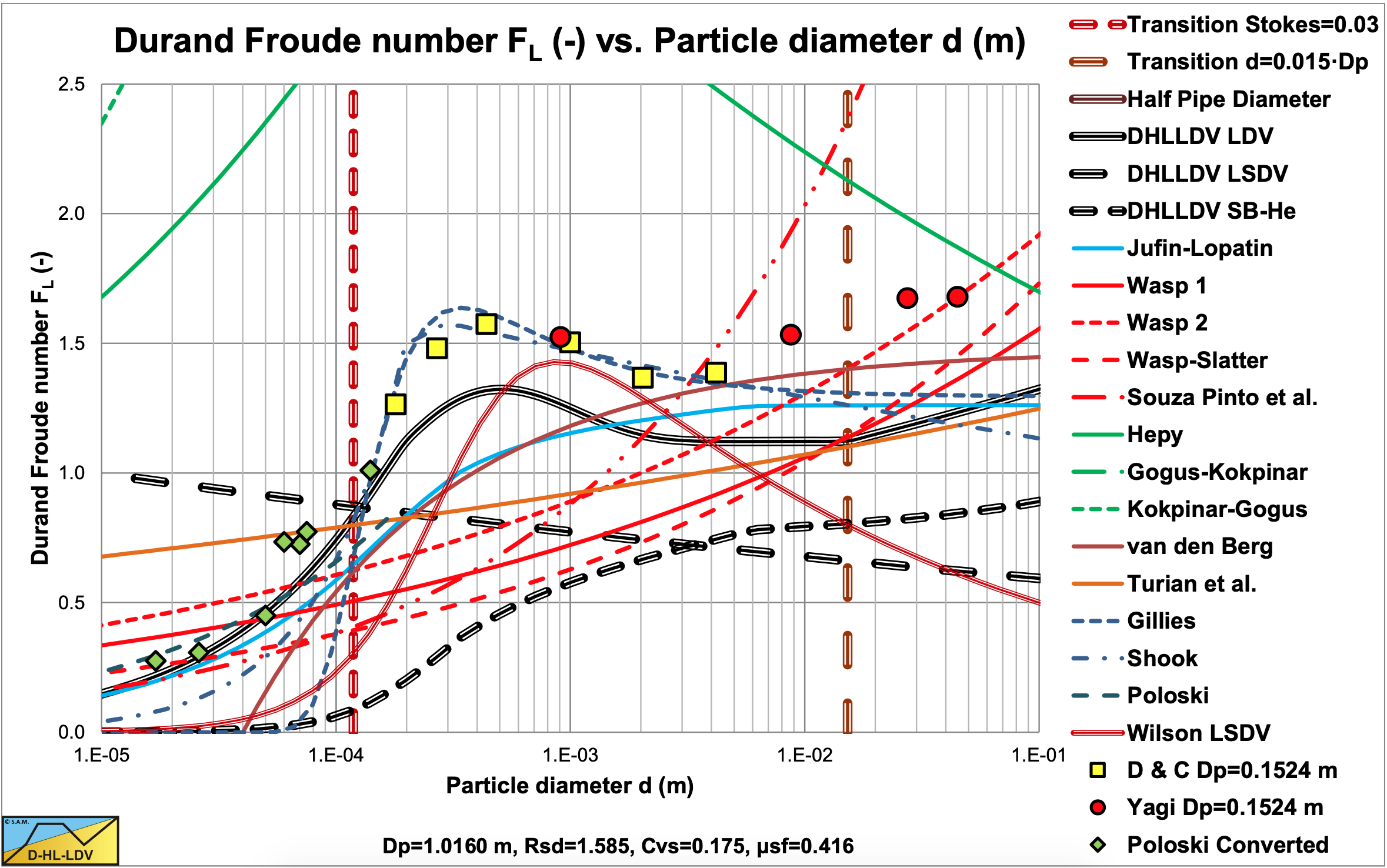
Figure 9.3-2 to Figure 9.3-11 show the Limit Deposit Velocities of DHLLDV, Durand and Condolios (1952), Jufin and Lopatin (1966), Wasp et al. (1970), Wasp and Slatter (2004), Souza Pinto et al. (2014), Hepy et al. (2008), Gogus and Kokpinar (1993), Kokpinar and Gogus (2001), Berg (1998), Turian et al. (1987) and Gillies (1993) for 10 pipe diameters. The figures also show the LSDV and the transition sliding bed to heterogeneous transport. The intersection between these two curves gives the smallest particle diameter where a sliding bed can exist.
The curves of Hepy et al. (2008), Gogus and Kokpinar (1993) and Kokpinar and Gogus (2001) show a maximum FL value for particles with a diameter near d = 0.5 mm. However these models show an increasing FL value with the pipe diameter, which contradicts the numerous experimental data, showing a slight decrease. The models of Turian et al. (1987) , Wasp et al. (1970), Wasp and Slatter (2004) and Souza Pinto et al. (2014) show an increasing FL value with increasing particle diameter and a slight decrease with the pipe diameter.
Jufin and Lopatin (1966) show an increase with the particle diameter and a slight decrease with the pipe diameter (power –1/6). The model of van den Berg (1998) shows an increasing FL with the particle diameter, but no dependency on the pipe diameter. Durand and Condolios (1952) did not give an equation but a graph. The data points as derived from the original publication in (1952) and from Durand (1953) are shown in the graphs. The data points show a maximum for d = 0.5 mm. They did not report any dependency on the pipe diameter. The model of Gillies (1993) tries to quantify the Durand and Condolios (1952) data points, but does not show any dependency on the pipe diameter for the FL Froude number. The increase of the FL value with the pipe diameter of the Hepy et al. (2008), Gogus and Kokpinar (1993) and Kokpinar and Gogus (2001) models is probably caused by the forced d/Dp relation. With a strong relation with the particle diameter and a weak relation for the pipe diameter, the pipe diameter will follow the particle diameter. Another reason may be the fact that they used pipe diameters up to 0.1524 m (6 inch) and the smaller the pipe diameter the more probable the occurrence of a sliding bed and other limiting conditions, due to the larger hydraulic gradient helping the bed to start sliding.
The figures show that for medium pipe diameters all models are close. The reason is probably that most experiments are carried out with medium pipe diameters. Only Jufin and Lopatin (1966) covered a range from 0.02 m to 0.9 m pipe diameters. Recently Thomas (2014) gave an overview and analysis of the LDV (or sometimes the LSDV). He repeated the findings that the LDV depends on the pipe diameter with a power smaller than 0.5 but larger than 0.1. The value of 0.1 is for very small particles, while for normal sand and gravels a power is expected between 1/3 according to Jufin and Lopatin (1966) and 1/2 according to Durand and Condolios (1952). Most equations are one term equations, making it impossible to cover all aspects of the LDV behavior. Only Gillies (1993) managed to construct an equation that gets close to the original Durand and Condolios (1952) graph.
The models analyzed result in a number of dominating parameters. These are the particle diameter d, the pipe diameter Dp, the liquid density ρl and kinematic viscosity \(\ v_{\mathrm{l}}\), the solids density ρs, the sliding friction coefficient μsf, the bed concentration Cvb and the spatial volumetric concentration Cvs. Derived parameters are the relative submerged density Rsd, the Darcy Weisbach friction factor for pure liquid flow λl and the thickness of the viscous sub-layer δv. Dimensionless numbers are not considered at first, since they may lead to wrong interpretations. Lately Lahiri (2009) performed an analysis using artificial neural network and support vector regression.
Azamathulla and Ahmad (2013) performed an analysis using adaptive neuro-fuzzy interference system and gene- expression programming. Although these methodologies may give good correlations, they do not explain the physics. Lahiri (2009) however did give statistical relations for the dependency on the volumetric concentration, the particle diameter, the pipe diameter and the relative submerged density. Resuming, the following conclusions can be drawn for sand and gravel:
The pipe diameter Dp: The LDV is proportional to the pipe diameter Dp to a power between 1/3 and 1/2 (about 0.4) for small to large particles (Thomas (1979), Wasp et al. (1977), Lahiri (2009) and Jufin and Lopatin (1966)) and a power of about 0.1 for very small particles (Thomas (1979), Wilson and Judge (1976), Sanders et al. (2004) and Poloski et al. (2010)).
The particle diameter d: The LDV has a lower limit for very small particles, after which it increases to a maximum at a particle diameter of about d = 0.5 mm (Thomas (1979), Thomas (2014), Durand and Condolios (1952), Gillies (1993) and Poloski et al. (2010)). For medium sized particles with a particle size d > 0.5 mm, the FL value decreases to a minimum for a particle size of about d = 2 mm (Durand and Condolios, 1952; Gillies, 1993; Poloski et al., 2010). Above 2 mm, the FL value will remain constant according to Durand and Condolios (1952) and Gillies (1993). For particles with d/Dp > 0.015, the Wilson et al. (1992) criterion for real suspension/saltation, the FL value increases again. This criterion is based on the ratio particle diameter to pipe diameter and will start at a large particle diameter with increasing pipe diameter. Yagi et al. (1972) reported many data points in this region showing an increasing FL value.
The relative submerged density Rsd: The relation between the LDV and the relative submerged density is not very clear, however the data shown by Kokpinar and Gogus (2001) and the conclusions of Lahiri (2009) show that the FL value decreases with increasing solids density and thus relative submerged density Rsd to a power of –0.1 to – 0.2.
The spatial volumetric concentration Cvs: The volumetric concentration leading to the maximum LDV is somewhere between 15% and 20% according to Durand and Condolios (1952). Lahiri (2009) reported a maximum at about 17.5%, while Poloski et al. (2010) derived 15%. This maximum LDV results from on one hand a linear increase of the sedimentation with the concentration and on the other hand a reduced sedimentation due to the hindered setting. These two counteracting phenomena result in a maximum, which is also present in the equation of the potential energy of the DHLLDV Framework. For small concentrations a minimum LDV is observed by Durand and Condolios (1952). This minimum LDV increases with the particle diameter and reaches the LDV of 20% at a particle diameter of 2 mm with a pipe diameter of 0.1524 m (6 inch).
For the dredging industry the Jufin and Lopatin (1966) equation gives a good approximation for sand and gravel, although a bit conservative. The model of van den Berg (1998) is suitable for large diameter pipes as used in dredging for sand and/or gravel, but underestimates the LDV for pipe diameters below 0.8 m. Both models tend to underestimate the LDV for particle diameters below 1 mm.
9.3.2 Conclusions Limit Deposit Velocity
The Limit Deposit Velocity (LDV) and the Limit of Stationary Deposit Velocity (LSDV) are distinguished. Wilson et al. (1992) use the LSDV, while Durand & Condolios (1952) and the DHLLDV Framework use the LDV. The LDV will always give higher FL values than the LSDV. Not because of scatter or because of a safety factor, but because of a different definition. The LDV (the line speed above which there is no stationary of sliding bed) always exists, the LSDV only at the lower boundary of a sliding bed region.
It should be noted that for small particles, the LDV and the transition of the heterogeneous regime to the ELM are very close. For very small particles however viscous effects may play a role, which is not taken into consideration here.
The graphs in Figure 9.3-2 to Figure 9.3-11 show a number of LDV models and also the LSDV of Wilson (1979), the LSDV of the DHLLDV Framework and the transition of the sliding bed to the heterogeneous regime according to the DHLLDV Framework. It should be noted that the LSDV of the Wilson model shows the maximum curve. It should further be noted that for the DHLLDV Framework a sliding bed can only exist if the transition velocity of the sliding bed regime to the heterogeneous regime is higher than the LSDV. If this is lower, a sliding bed will never exist. The bed will be completely suspended before the bed could ever start sliding.
The data points in the graphs are all for a Dp=0.1524 m (6 inch) pipe. Durand and Condolios (1952) assumed that their Froude number is independent of the pipe diameter. From all the experiments it appeared that the Froude number decreases slightly with the pipe diameter.
9.3.3 Graphs