10.5: A Segmented Pipeline System
- Page ID
- 32676
Splitting the pressure losses over n pipe segments gives a more detailed impression of the pressure losses in a system with more than 1 pump. The pumps are numbered from number 1 to number n. The pipe segments are numbered from number 0 (the suction pipe) to number n. One could consider the hydrostatic pressure p0,in at the suction mouth as the result of a virtual pump number 0, the result of the layer of water above the suction mouth plus the atmospheric pressure above the waterline. First the pressure losses in the suction pipe, resulting in the absolute pressure at the entrance of the first real pump (pump 1) and showing whether there will be cavitation, will be determined. Next equations are derived for all other pipe segments. The mixture flow Qm is either a constant in the whole system, or increases slightly because of the gland water in each pump. The latter may result in a decreasing mixture density after each pump. The pipe diameter Dp and thus the line speed vls may differ for each pipe segment.
Absolute pressure start with the symbol p, while pressure difference start with Δp. So pump head and pipeline resistance are pressure differences.
10.5.1 The Suction Pipe
The cross section of the suction pipe (segment 0) is:
\[\ \mathrm{A}_{\mathrm{p}, \mathrm{0}}=\frac{\pi}{4} \cdot \mathrm{D}_{\mathrm{p}, \mathrm{0}}^{\mathrm{2}}\]
The line speed in the suction pipe, assuming a mixture flow Qm,0, is:
\[\ \mathrm{v}_{\mathrm{l} \mathrm{s}, \mathrm{0}}=\frac{\mathrm{Q}_{\mathrm{m}, \mathrm{0}}}{\mathrm{A}_{\mathrm{p}, \mathrm{0}}}\]
The pressure losses from the suction mouth to the entrance of the first pump (segment 0) are:
\[\ \begin{array}{ll}\Delta \mathrm{p}_{\mathrm{m}, \mathrm{0}}&=\frac{\mathrm{1}}{2} \cdot \rho_{\mathrm{m}, \mathrm{0}} \cdot \mathrm{v}_{\mathrm{l} \mathrm{s}, \mathrm{0}}^{\mathrm{2}}
&\text{(Acceleration losses)}\\
&+\lambda_{1,0} \cdot \frac{\mathrm{L}_{0}}{\mathrm{D}_{\mathrm{p}, 0}} \cdot \frac{1}{2} \cdot \rho_{\mathrm{l}} \cdot \mathrm{v}_{\mathrm{l} \mathrm{s}, 0}^{2} & \text {(Darcy Weisbach friction losses) } \\
&+\frac{1}{2} \cdot \rho_{\mathrm{m}, 0} \cdot \mathrm{v}_{\mathrm{l} \mathrm{s}, 0}^{2} \cdot \sum_{\mathrm{l}=1}^{\mathrm{m}_{0}} \xi_{\mathrm{l},0} & \text {(Losses due to } \mathrm{m}_0 \text{ fittings) }\\
&+\rho_{\mathrm{m}, 0} \cdot \mathrm{g} \cdot \mathrm{L}_{0} \cdot \sin \left(\theta_{0}\right)
&\text{(Losses due to pipe inclination or elevation)}\\
&+\rho_{\mathrm{l}} \cdot \mathrm{g} \cdot \mathrm{L}_{0} \cdot \mathrm{R}_{\mathrm{s} \mathrm{d}} \cdot \mathrm{C}_{\mathrm{v} \mathrm{t}} \cdot \mathrm{E}_{\mathrm{r h g}, \mathrm{0}}&\text{(Losses due to the solids effect)}\\
\text{With: }&\mathrm{H}_{\mathrm{0}, \mathrm{o u t}}-\mathrm{H}_{\mathrm{0}, \mathrm{i n}}=\mathrm{L}_{\mathrm{0}} \cdot \sin \left(\theta_{\mathrm{0}}\right)\end{array}\]
The mixture density is based on the delivered/transport volumetric concentration.
The absolute hydrostatic pressure at the inlet of the suction mouth of the cutter head or in the drag head p0,in is the elevation at the waterline Hwl (which is defined as zero) minus the elevation of the suction mouth H0,in (which is a negative elevation) times the liquid (water) density and the gravitational constant plus the atmospheric pressure:
\[\ \mathrm{p}_{0, \mathrm{in}}=\rho_{\mathrm{l}} \cdot \mathrm{g} \cdot\left(\mathrm{H}_{\mathrm{wl}}-\mathrm{H}_{0, \mathrm{in}}\right)+\mathrm{p}_{\mathrm{atm}}\]
This gives for the absolute pressure at the inlet of the first pump, the absolute pressure at the inlet of the suction pipe p0,in minus the pressure losses in the suction pipe Δpm,0 (segment 0):
\[\ \mathrm{p}_{0, \text { out }}=\mathrm{p}_{0, \text { in }}-\Delta \mathrm{p}_{\mathrm{m}, \mathrm{0}}\]
The absolute pressure at the inlet of the first pump is p0,out and should be above a certain minimum pcav to avoid cavitation. Although theoretically the cavitation pressure is almost absolute 0, in reality locally cavitation may appear at higher absolute mean pressures, because locally velocities may differ from the mean velocity.
\[\ \mathrm{p}_{\mathrm{0}, \mathrm{o u t}}>\mathrm{p}_{\mathrm{c a v}}\]
In a stationary situation, the mixture density ρm,0 has to be smaller than a certain limit to avoid cavitation in the first pump. So the condition is:
\[\ \begin{array}{left}\mathrm{p}_{0, \mathrm{in}}-\Delta \mathrm{p}_{\mathrm{m}, 0}>\mathrm{p}_{\mathrm{c a v}} \quad \mathrm{o r} \quad \mathrm{p}_{0, \mathrm{in}}-\mathrm{p}_{\mathrm{c a v}}-\Delta \mathrm{p}_{\mathrm{m}, 0}>\mathrm{0}\\
\rho_{\mathrm{l}} \cdot \mathrm{g} \cdot\left(\mathrm{H}_{\mathrm{wl}}-\mathrm{H}_{0, \mathrm{in}}\right)+\mathrm{p}_{\mathrm{atm}}-\mathrm{p}_{\mathrm{cav}}-\Delta \mathrm{p}_{\mathrm{m}, 0}>\mathrm{0}\end{array}\]
Substituting the pressure losses in the suction pipe gives:
\[\ \begin{array}{left} \rho_{\mathrm{l}} \cdot \mathrm{g} \cdot\left(\mathrm{H}_{\mathrm{w} \mathrm{l}}-\mathrm{H}_{\mathrm{0}, \mathrm{i n}}\right)+\mathrm{p}_{\mathrm{a t m}}-\mathrm{p}_{\mathrm{c a v}}-\lambda_{\mathrm{l}, \mathrm{0}} \cdot \frac{\mathrm{L}_{\mathrm{0}}}{\mathrm{D}_{\mathrm{p}, \mathrm{0}}} \cdot \frac{\mathrm{1}}{2} \cdot \rho_{\mathrm{l}} \cdot \mathrm{v}_{\mathrm{l} \mathrm{s}, \mathrm{0}}^{\mathrm{2}}-\rho_{\mathrm{l}} \cdot \mathrm{g} \cdot \mathrm{L}_{\mathrm{0}} \cdot \mathrm{R}_{\mathrm{s d}} \cdot \mathrm{C}_{\mathrm{v t}} \cdot \mathrm{E}_{\mathrm{r h g}, \mathrm{0}}\\
-\frac{\mathrm{1}}{2} \cdot \rho_{\mathrm{m}, \mathrm{0}} \cdot \mathrm{v}_{\mathrm{l s}, \mathrm{0}}^{2}-\frac{\mathrm{1}}{2} \cdot \rho_{\mathrm{m}, \mathrm{0}} \cdot \mathrm{v}_{\mathrm{l s}, \mathrm{0}}^{2} \cdot \sum_{\mathrm{l}=\mathrm{1}}^{\mathrm{m}_{0}} \xi_{\mathrm{l}, \mathrm{0}}-\rho_{\mathrm{m}, \mathrm{0}} \cdot \mathrm{g} \cdot \mathrm{L}_{\mathrm{0}} \cdot \sin \left(\theta_{0}\right)>\mathrm{0}\end{array}\]
This gives for the maximum mixture density not having cavitation:
\[\ \mathrm{\rho_{m,0}<\frac{\rho_l\cdot g \cdot \left(H_{wl}-H_{0,in} \right)+P_{atm}-{P_{cav}}-
\lambda_{l,0}\cdot \frac{L_0}{D_{p,0}}\cdot \frac{1}{2}\cdot \rho_l \cdot v_{ls,0}^2-\rho_l \cdot g \cdot L_0 \cdot R_{sd}\cdot C_{tv}\cdot E_{rhg,0}}{\frac{1}{2}\cdot v_{ls,0}^2+\frac{1}{2}\cdot v_{ls,0}^2\cdot \sum_{l=1}^{m_o}\xi_{l,0}+g\cdot L_0 \cdot sin\left(\theta_0 \right)}} \]
10.5.2 Other Pipe Segments
All other pipe segments start after a pump with index i and also have the index i (so segment i). Since each pipe segment may have a different pipe diameter, first the pipe cross section and the line speed in the pipe segment have to be determined. The flow Qm,i of course is the same in each pipe segment, because of continuity considerations. However if gland water flow is taken into consideration, after each pump the flow may increaseslightly. That’s the reason why in the equations the flow also has an indez i. In most cases the gland water flow is neglected and the flow in each pipe segment is the same.
The cross section of a pipe segment (segment i) is:
\[\ \mathrm{A}_{\mathrm{p}, \mathrm{i}}=\frac{\pi}{4} \cdot \mathrm{D}_{\mathrm{p}, \mathrm{i}}^{2}\]
The flow in pipe section i, corrected for gland water flow is:
\[\ \mathrm{Q}_{\mathrm{m}, \mathrm{i}}=\mathrm{Q}_{\mathrm{m}, \mathrm{i}-\mathrm{1}}+\mathrm{Q}_{\mathrm{g} \mathrm{w}, \mathrm{i}}\]
The line speed in the pipe segment, assuming a mixture flow Qm,i, is:
\[\ \mathrm{v}_{\mathrm{l} \mathrm{s}, \mathrm{i}}=\frac{\mathrm{Q}_{\mathrm{m}, \mathrm{i}}}{\mathrm{A}_{\mathrm{p}, \mathrm{i}}}\]
The pressure losses of pipe segment i with an inclined pipe are:
\[\ \begin{array}{left}\Delta \mathrm{p}_{\mathrm{m}, \mathrm{i}}=\frac{1}{2} \cdot \rho_{\mathrm{m}, \mathrm{i}} \cdot\left(\mathrm{v}_{\mathrm{ls}, \mathrm{i}}^{2}-\mathrm{v}_{\mathrm{l} \mathrm{s}, \mathrm{i}-1}^{\mathrm{2}}\right)+\lambda_{\mathrm{l}, \mathrm{i}} \cdot \frac{\mathrm{L}_{\mathrm{i}}}{\mathrm{D}_{\mathrm{p}, \mathrm{i}}} \cdot \frac{1}{2} \cdot \rho_{\mathrm{l}} \cdot \mathrm{v}_{\mathrm{l} \mathrm{s}, \mathrm{i}}^{2}+\frac{1}{2} \cdot \rho_{\mathrm{m}, \mathrm{i}} \cdot \mathrm{v}_{\mathrm{ls}, \mathrm{i}}^{2} \cdot \sum_{\mathrm{l}=1}^{\mathrm{m}_{\mathrm{i}}} \xi_{\mathrm{l}, \mathrm{i}}
+\rho_{\mathrm{m}, \mathrm{i}} \cdot \mathrm{g} \cdot \mathrm{L}_{\mathrm{i}} \cdot \sin \left(\theta_{\mathrm{i}}\right)+\rho_{\mathrm{l}} \cdot \mathrm{g} \cdot \mathrm{L}_{\mathrm{i}} \cdot \mathrm{R}_{\mathrm{s} \mathrm{d}} \cdot \mathrm{C}_{\mathrm{v} \mathrm{t}} \cdot \mathrm{E}_{\mathrm{r h g}, \mathrm{i}}\\
\text{W} \mathrm{i t h}: \quad \mathrm{H}_{\mathrm{i}, \mathrm{o} \mathrm{u t}}-\mathrm{H}_{\mathrm{i}, \mathrm{i} \mathrm{n}}=\mathrm{L}_{\mathrm{i}} \cdot \sin \left(\theta_{\mathrm{i}}\right)\end{array}\]
In case there is no pipe inclination, but a vertical part in the pipe section, the 4th term can be replaced by:
\[\ \Delta \mathrm{p}_{\mathrm{m}, \mathrm{i}}=\frac{1}{2} \cdot \rho_{\mathrm{m}, \mathrm{i}} \cdot\left(\mathrm{v}_{\mathrm{l} \mathrm{s}, \mathrm{i}}^{2}-\mathrm{v}_{\mathrm{l} \mathrm{s}, \mathrm{i}-1}^{2}\right)+\lambda_{\mathrm{l}, \mathrm{i}} \cdot \frac{\mathrm{L}_{\mathrm{i}}}{\mathrm{D}_{\mathrm{p}, \mathrm{i}}} \cdot \frac{1}{2} \cdot \rho_{\mathrm{l}} \cdot \mathrm{v}_{\mathrm{l} \mathrm{s}, \mathrm{i}}^{2}+\cdot \frac{1}{2} \cdot \rho_{\mathrm{m}, \mathrm{i}} \cdot \mathrm{v}_{\mathrm{l} \mathrm{s}, \mathrm{i}}^{2} \cdot \sum_{\mathrm{l}=1}^{\mathrm{m}_{\mathrm{i}}} \xi_{\mathrm{l}, \mathrm{i}}
+\rho_{\mathrm{m}, \mathrm{i}} \cdot \mathrm{g} \cdot\left(\mathrm{H}_{\mathrm{i}, \mathrm{o u t}}-\mathrm{H}_{\mathrm{i}, \mathrm{i} \mathrm{n}}\right)+\rho_{\mathrm{l}} \cdot \mathrm{g} \cdot \mathrm{L}_{\mathrm{i}} \cdot \mathrm{R}_{\mathrm{s d}} \cdot \mathrm{C}_{\mathrm{v t}} \cdot \mathrm{E}_{\mathrm{r h g}, \mathrm{i}}\]
10.5.3 Adding Pump Head to the Equations
Now suppose each pump has a pump head, depending on the flow through the pump, the mixture density and the particle diameter. The latter influences the efficiency of the pump. Small particles have hardly any influence, but large particles, like gravel, do. The pump head is named Δpp,i(Qm,i-1,ρm,d). The absolute pressure at the entrance of pump k+1, pe,k+1, so at the end of segment k, can now be determined with:
\[\ \begin{array}{left} \mathrm{p}_{\mathrm{e}, \mathrm{k}+1}&= \rho_{\mathrm{l}} \cdot \mathrm{g} \cdot\left(\mathrm{H}_{\mathrm{w} \mathrm{l}}-\mathrm{H}_{0, \mathrm{i n}}\right)+\mathrm{p}_{\mathrm{a t m}}-\Delta \mathrm{p}_{\mathrm{m}, \mathrm{0}}-\sum_{\mathrm{i}=1}^{\mathrm{k}}\left(\frac{1}{2} \cdot \rho_{\mathrm{m}, \mathrm{i}} \cdot\left(\mathrm{v}_{\mathrm{l} \mathrm{s}, \mathrm{i}}^{2}-\mathrm{v}_{\mathrm{ls}, \mathrm{i}-1}^{2}\right)\right) \\
&-\sum_{\mathrm{i}=1}^{\mathrm{k}}\left(\lambda_{\mathrm{l}, \mathrm{i}} \cdot \frac{\mathrm{L}_{\mathrm{i}}}{\mathrm{D}_{\mathrm{p}, \mathrm{i}}} \cdot \frac{\mathrm{1}}{2} \cdot \rho_{\mathrm{l}} \cdot \mathrm{v}_{\mathrm{ls}, \mathrm{i}}^{2}\right)-\sum_{\mathrm{i}=1}^{\mathrm{k}}\left(\frac{\mathrm{1}}{2} \cdot \rho_{\mathrm{m}, \mathrm{i}} \cdot \mathrm{v}_{\mathrm{ls}, \mathrm{i}}^{2} \cdot \sum_{\mathrm{l}=1}^{\mathrm{m}_{\mathrm{i}}} \xi_{\mathrm{l}, \mathrm{i}}\right) \\ &-\sum_{\mathrm{i}=\mathrm{1}}^{\mathrm{k}}\left(\rho_{\mathrm{m}, \mathrm{i}} \cdot \mathrm{g} \cdot \mathrm{L}_{\mathrm{i}} \cdot \sin \left(\theta_{\mathrm{i}}\right)\right)-\rho_{\mathrm{l}} \cdot \mathrm{g} \cdot \mathrm{R}_{\mathrm{s} \mathrm{d}} \cdot \mathrm{C}_{\mathrm{v} \mathrm{t}} \cdot \sum_{\mathrm{i}=1}^{\mathrm{k}}\left(\mathrm{L}_{\mathrm{i}} \cdot \mathrm{E}_{\mathrm{r h g}, \mathrm{i}}\right)+\sum_{\mathrm{i}=\mathrm{1}}^{\mathrm{k}}\left(\Delta \mathrm{p}_{\mathrm{p}, \mathrm{i}}\right) \end{array}\]
The absolute pressure at the discharge of pump k+1, pd,k+1, can now be determined with:
\[\ \begin{array}{left} \mathrm{p}_{\mathrm{d}, \mathrm{k}+1}&= \rho_{\mathrm{l}} \cdot \mathrm{g} \cdot\left(\mathrm{H}_{\mathrm{w} \mathrm{l}}-\mathrm{H}_{0, \mathrm{i n}}\right)+\mathrm{p}_{\mathrm{a t m}}-\Delta \mathrm{p}_{\mathrm{m}, \mathrm{0}}-\sum_{\mathrm{i}=1}^{\mathrm{k}}\left(\frac{1}{2} \cdot \rho_{\mathrm{m}, \mathrm{i}} \cdot\left(\mathrm{v}_{\mathrm{l} \mathrm{s}, \mathrm{i}}^{2}-\mathrm{v}_{\mathrm{ls}, \mathrm{i}-1}^{2}\right)\right) \\
&-\sum_{\mathrm{i}=1}^{\mathrm{k}}\left(\lambda_{\mathrm{l}, \mathrm{i}} \cdot \frac{\mathrm{L}_{\mathrm{i}}}{\mathrm{D}_{\mathrm{p}, \mathrm{i}}} \cdot \frac{\mathrm{1}}{2} \cdot \rho_{\mathrm{l}} \cdot \mathrm{v}_{\mathrm{ls}, \mathrm{i}}^{2}\right)-\sum_{\mathrm{i}=1}^{\mathrm{k}}\left(\frac{\mathrm{1}}{2} \cdot \rho_{\mathrm{m}, \mathrm{i}} \cdot \mathrm{v}_{\mathrm{ls}, \mathrm{i}}^{2} \cdot \sum_{\mathrm{l}=1}^{\mathrm{m}_{\mathrm{i}}} \xi_{\mathrm{l}, \mathrm{i}}\right) \\ &-\sum_{\mathrm{i}=\mathrm{1}}^{\mathrm{k}}\left(\rho_{\mathrm{m}, \mathrm{i}} \cdot \mathrm{g} \cdot \mathrm{L}_{\mathrm{i}} \cdot \sin \left(\theta_{\mathrm{i}}\right)\right)-\rho_{\mathrm{l}} \cdot \mathrm{g} \cdot \mathrm{R}_{\mathrm{s} \mathrm{d}} \cdot \mathrm{C}_{\mathrm{v} \mathrm{t}} \cdot \sum_{\mathrm{i}=1}^{\mathrm{k}}\left(\mathrm{L}_{\mathrm{i}} \cdot \mathrm{E}_{\mathrm{r h g}, \mathrm{i}}\right)+\sum_{\mathrm{i}=\mathrm{1}}^{\mathrm{k}}\left(\Delta \mathrm{p}_{\mathrm{p}, \mathrm{i}}\right) \end{array}\]
At the end (the discharge) of the pump/pipeline system the pressure is atmospheric again in a stationary situation. This give the following equation:
\[\ \begin{array}{left} \mathrm{p}_{\mathrm{atm}}&= \rho_{\mathrm{l}} \cdot \mathrm{g} \cdot\left(\mathrm{H}_{\mathrm{w} \mathrm{l}}-\mathrm{H}_{0, \mathrm{i n}}\right)+\mathrm{p}_{\mathrm{a t m}}-\Delta \mathrm{p}_{\mathrm{m}, \mathrm{0}}-\frac{1}{2} \cdot\sum_{\mathrm{i}=1}^{\mathrm{n}}\left( \rho_{\mathrm{m}, \mathrm{i}} \cdot\left(\mathrm{v}_{\mathrm{l} \mathrm{s}, \mathrm{i}}^{2}-\mathrm{v}_{\mathrm{ls}, \mathrm{i}-1}^{2}\right)\right) \\
&-\sum_{\mathrm{i}=1}^{\mathrm{n}}\left(\lambda_{\mathrm{l}, \mathrm{i}} \cdot \frac{\mathrm{L}_{\mathrm{i}}}{\mathrm{D}_{\mathrm{p}, \mathrm{i}}} \cdot \frac{\mathrm{1}}{2} \cdot \rho_{\mathrm{l}} \cdot \mathrm{v}_{\mathrm{ls}, \mathrm{i}}^{2}\right)-\sum_{\mathrm{i}=1}^{\mathrm{n}}\left(\frac{\mathrm{1}}{2} \cdot \rho_{\mathrm{m}, \mathrm{i}} \cdot \mathrm{v}_{\mathrm{ls}, \mathrm{i}}^{2} \cdot \sum_{\mathrm{l}=1}^{\mathrm{m}_{\mathrm{i}}} \xi_{\mathrm{l}, \mathrm{i}}\right) \\ &-\sum_{\mathrm{i}=\mathrm{1}}^{\mathrm{n}}\left(\rho_{\mathrm{m}, \mathrm{i}} \cdot \mathrm{g} \cdot \mathrm{L}_{\mathrm{i}} \cdot \sin \left(\theta_{\mathrm{i}}\right)\right)-\rho_{\mathrm{l}} \cdot \mathrm{g} \cdot \mathrm{R}_{\mathrm{s} \mathrm{d}} \cdot \mathrm{C}_{\mathrm{v} \mathrm{t}} \cdot \sum_{\mathrm{i}=1}^{\mathrm{n}}\left(\mathrm{L}_{\mathrm{i}} \cdot \mathrm{E}_{\mathrm{r h g}, \mathrm{i}}\right)+\sum_{\mathrm{i}=\mathrm{1}}^{\mathrm{n}}\left(\Delta \mathrm{p}_{\mathrm{p}, \mathrm{i}}\right) \end{array}\]
One could even make the equations more detailed by dividing pipe segments into pipe sections. At the point where a pipe segment is split into sections, a virtual pump with zero head could be added. This way the above equations are also valid for a system where the segment boundaries do not have to be a pump, the entrance or the discharge of the pipeline, but can also be a zero head virtual pump. This enables to create a detailed graph of the pressure in the pipeline as a function of the distance from the entrance.
Now assuming a constant pipe diameter in the whole system, no gland water, and a constant mixture density in the whole system. Equation (10.5-17) can be reduced to:
\[\ \begin{array}{left}\rho_{\mathrm{l}} \cdot \mathrm{g} \cdot\left(\mathrm{H}_{\mathrm{wl}}-\mathrm{H}_{0, \mathrm{in}}\right)+\sum_{\mathrm{i}=1}^{\mathrm{n}}\left(\Delta \mathrm{p}_{\mathrm{p}, \mathrm{i}}\right)-\frac{1}{2} \cdot \rho_{\mathrm{m}} \cdot \mathrm{v}_{\mathrm{l} \mathrm{s}}^{2}-\lambda_{\mathrm{l}} \cdot \frac{\mathrm{L}_{\mathrm{tot} }}{\mathrm{D}_{\mathrm{p}}} \cdot \frac{\mathrm{1}}{2} \cdot \rho_{\mathrm{l}} \cdot \mathrm{v}_{\mathrm{l} \mathrm{s}}^{2}-\frac{1}{2} \cdot \rho_{\mathrm{m}} \cdot \mathrm{v}_{\mathrm{l} \mathrm{s}}^{2} \cdot \sum_{\mathrm{i}=0}^{\mathrm{n}}\left(\sum_{\mathrm{l}=1}^{\mathrm{m}_{\mathrm{i}}} \xi_{\mathrm{l}, \mathrm{i}}\right)
-\rho_{\mathrm{m}} \cdot \mathrm{g} \cdot\left(\mathrm{H}_{\mathrm{n}, \mathrm{o} \mathrm{u} t}-\mathrm{H}_{0, \mathrm{in}}\right)-\rho_{\mathrm{l}} \cdot \mathrm{g} \cdot \mathrm{L}_{\mathrm{t} \mathrm{o} \mathrm{t}} \cdot \mathrm{R}_{\mathrm{s} \mathrm{d}} \cdot \mathrm{C}_{\mathrm{v} \mathrm{t}} \cdot \mathrm{E}_{\mathrm{r h g}}=\mathrm{0}\\
\text{With: }\quad \mathrm{L}_{\mathrm{t o t}}=\sum_{\mathrm{i}=0}^{\mathrm{n}}\left(\mathrm{L}_{\mathrm{i}}\right)\end{array}\]
Or using the pipeline resistance pressure Δpm from equation (10.1-1):
\[\ \rho_{\mathrm{l}} \cdot \mathrm{g} \cdot\left(\mathrm{H}_{\mathrm{wl}}-\mathrm{H}_{0, \mathrm{in}}\right)+\sum_{\mathrm{i}=1}^{\mathrm{n}}\left(\Delta \mathrm{p}_{\mathrm{p}, \mathrm{i}}\right)-\Delta \mathrm{p}_{\mathrm{m}}=\mathrm{0}\]
So in the working point there is an equilibrium between the sum of the hydrostatic pressure in the suction mouth and the added heads of all the pumps on one hand and the total pipeline resistance on the other hand. If there is no equilibrium, the mixture is either accelerating or decelerating in order to reach an equilibrium, which is described with the following equation:
\[\ \rho_{\mathrm{l}} \cdot \mathrm{g} \cdot\left(\mathrm{H}_{\mathrm{wl} }-\mathrm{H}_{0, \mathrm{in}}\right)+\sum_{\mathrm{i}=1}^{\mathrm{n}}\left(\Delta \mathrm{p}_{\mathrm{p}, \mathrm{i}}\right)-\Delta \mathrm{p}_{\mathrm{m}}=\rho_{\mathrm{m}} \cdot \mathrm{L}_{\mathrm{tot}} \cdot \dot{\mathrm{v}}_{\mathrm{ls}}\]
If the left hand side is positive there is acceleration, if it’s negative there is deceleration.
With the derived equations one can construct a detailed graph of the pressure in the pipeline versus the length of the pipeline and check whether cavitation occurs at the entrance of one of the pumps.
Figure 10.5-1 shows an example of a pump/pipeline system with a ladder pump, a main pump and a booster pump.
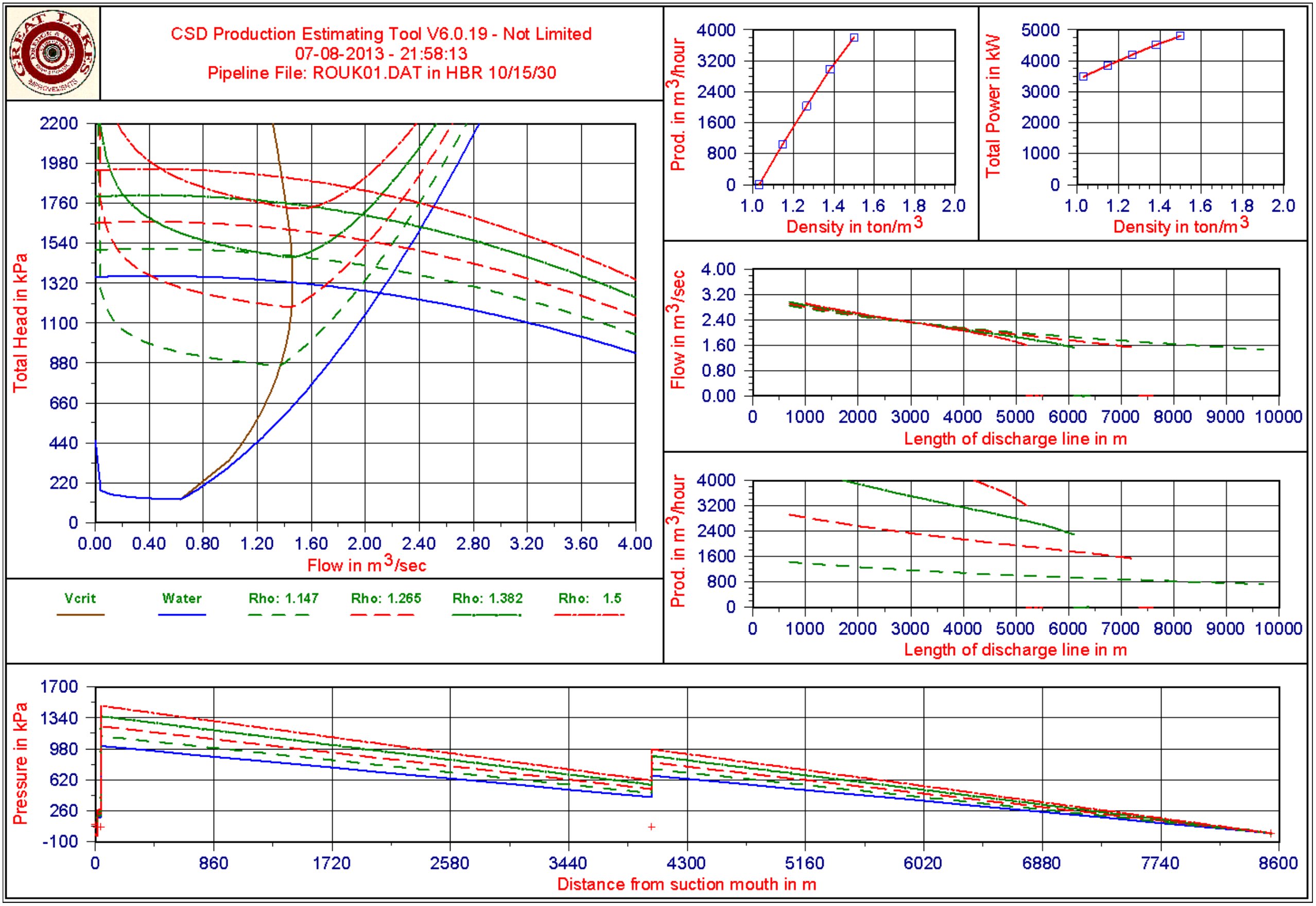
10.5.4 The Inertial Effects in the Pipeline
A steady state process requires a constant mixture density and solids properties in the system and thus at the suction mouth. In practice it is known, that the solids properties and the mixture density change with respect to time. As a result, the pump discharge pressure and vacuum will change with respect to time and the pipeline resistance will change with respect to time and place. A change of the discharge pressure of a pump will result in a change of the torque on the axis of the pump drive on one hand and in a change of the flow velocity on the other hand. The mixture in the pipeline has to accelerate or decelerate. Since centrifugal pumps respond to a change in density and solids properties at the moment the mixture passes the pump, while the pipeline resistance is determined by the contents of the pipeline as a whole, this forms a complex dynamic system with different time constants.
The inertial pressure of the mixture has to be added to the resistance of the mixture (see equation ). In fact, the inertial pressure is always equal to the difference between the total pressure generated by the pumps plus the absolute pressure at the suction mouth on one hand and the total resistance of the mixture in the pipeline system on the other hand. If this difference is positive (for example the pump pressure has increased due to an increase of the mixture density), the mixture will accelerate. If negative, the mixture will decelerate. As a result of the acceleration and deceleration, the mixture velocity (line speed) will vary as a function of time.
To realize a stable dredging process, it is required to have a line speed that will not vary too much. The line speed can be controlled by varying the revolutions of one of the dredge pumps, where the last pump is preferred.
From the above one can distinguish the different effects by the time they require to change/occur:
- Very fast (within a second), the change in discharge pressure of a centrifugal pump due to a sudden change of the mixture density in the pump.
- Fast (seconds), the change in revolutions of the pump drive and the change in line speed (acceleration and deceleration).
- Slow (minutes), filling up the pipeline with mixture or a change in mixture content. In large diameter pipelines this may take 2-2.5 minutes per kilometer of pipeline length.
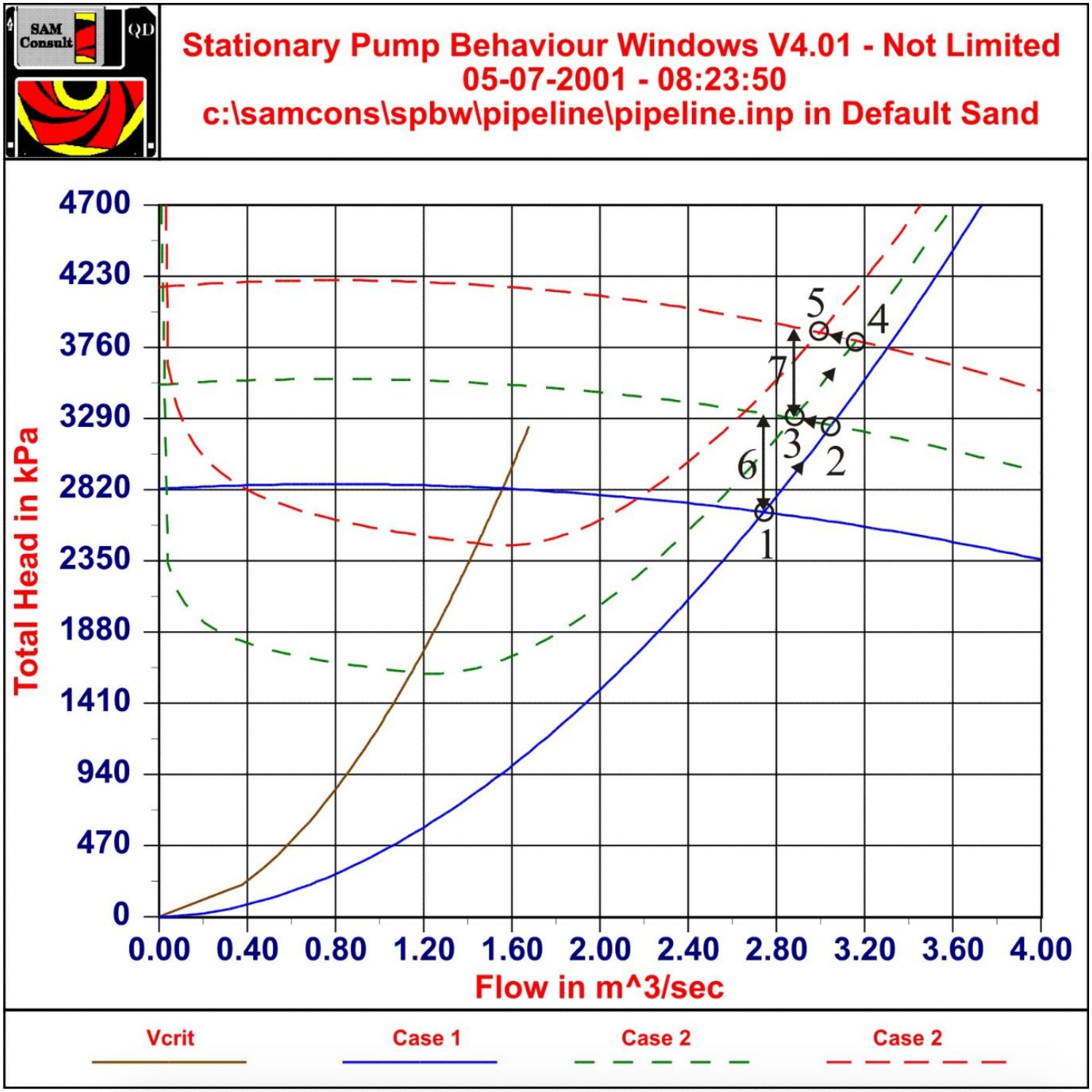
Figure 10.5-2 is a representation of a number of phenomena that occur subsequently when the system (Figure 10.1-1) filled with water, is filled with mixture with a density of 1.6 ton/m3. In this figure case 1 represents the system and the pump curve for the system filled with water. Case 2 represents the system with the pipeline filled with mixture up to a point just before the 3rd pump (the booster pump). Case 3 represents the system filled entirely with the mixture.
Now, what happens if a system filled with water is continuously filled with the mixture?
First the working point is point 1 in Figure 10.5-2. This is the intersection point of the pump and system curves for water. When mixture enters the system, within a few (about 8) seconds the mixture has reached the ladder and main pump, since the distance is only about 44 m and the line speed about 5 m/sec. At that moment, the discharge pressure of the ladder pump and main pump increase proportionally to the pressure matching the mixture density, resulting in a pump curve according to case 2 and a working point 2. The flow and thus the line speed will not change instantly because of the inertia of the fluid and solids mass in the pipeline. Number 6 shows the excess pressure caused by the sudden increase of the discharge pressure of the first two pumps. This excess pressure has to take care of the acceleration of the pipeline contents. This acceleration will take in the order of 10-20 seconds.
The filling of the system continues and the resistance of the mixture slowly increases, so the working point moves from point 2 to point 3. With the line speed of 5 m/s, this will take about 400 seconds or almost 7 minutes. When the mixture reaches the booster pump, at once the discharge pressure increases, resulting in the pump curve according to case 3, the top pump curve. The working point will move to point 4, while 7 represents the excess pressure causing the acceleration of the pipeline contents. Moving from 3 to 4 will take 10-20 seconds. When the pipeline continues to be filled with mixture, the resistance increases, resulting in the working point moving from 4 to 5 in about 400 seconds.
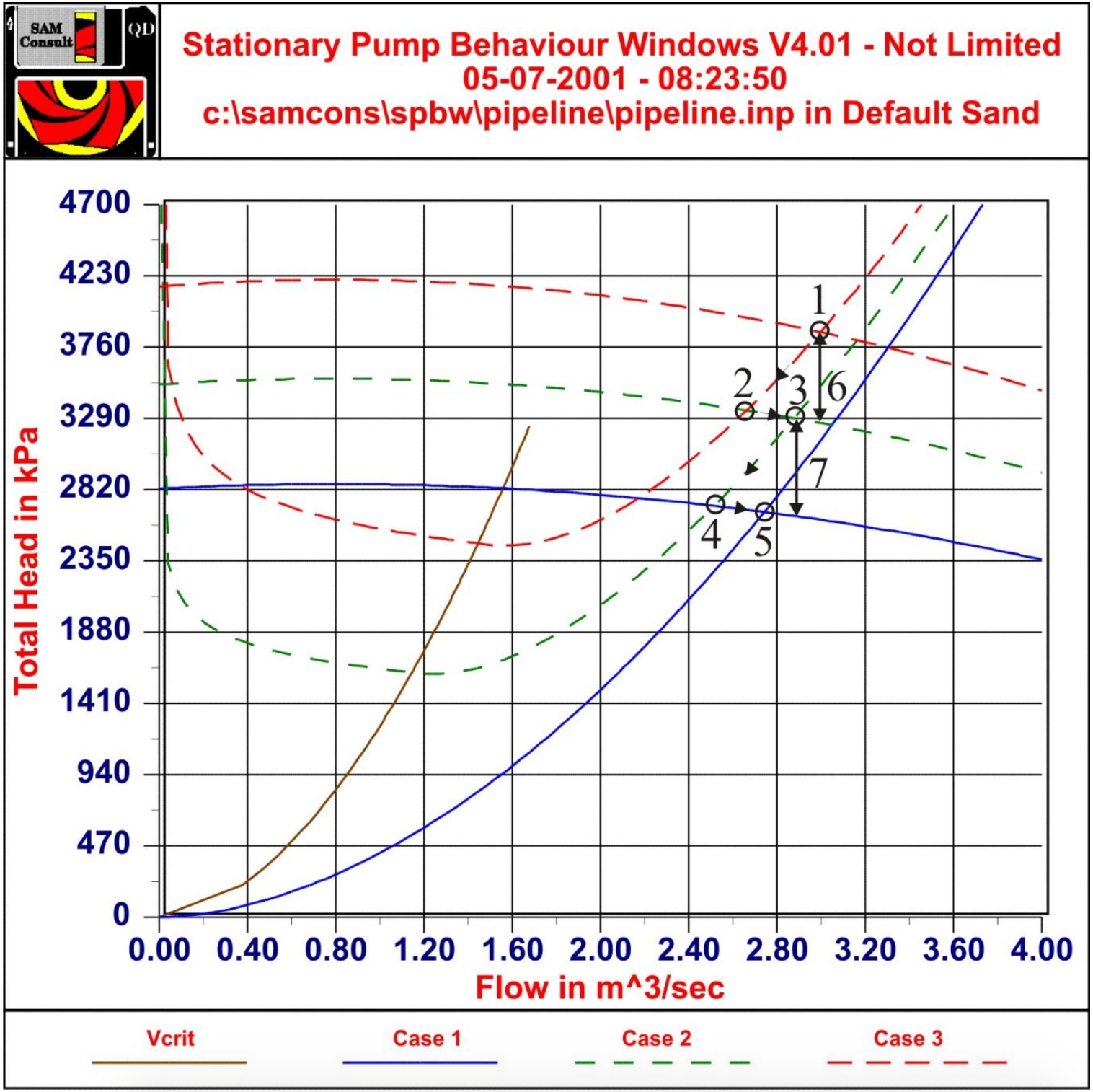
Figure 10.5-3 shows the same procedure for a pipeline filled with a mixture of density 1.6 ton/m3. In this case the pipeline, containing mixture of 1.6 ton/m3, is filled with water, resulting in decreasing discharge pressures and pipeline resistance. The procedure is almost the inverse, but Figure 10.5-3 shows that the path followed is different. In working point 1, all the pumps and the pipeline are filled with the mixture. When the water reaches the ladder and main pump, the pump head is decreased to case 2 and the new working point is point 2. Number 6 gives the deceleration pressure, so the contents of the pipeline will decelerate from 1 to 2 in about 10-20 seconds. From 2-3 the pipeline is filled with water up to the booster pump, resulting in a decrease of the pipeline resistance, taking about 400 seconds. When the water reaches the booster pump, the pump head curve decreases again to case 1, resulting in working point 4. Again it takes 10-20 seconds to move from point 3 to point 4. At last the pipeline behind the booster pump is filled with water, resulting in a decrease of the pipeline resistance, taking about 400 seconds. The final working point is point 5. Both Figure 10.5-2 and Figure 10.5-3 give an example of the non- stationary effects in a multi-pump/pipeline system.


