2.11: Summary

Last updated
Save as PDF

Page ID: 33353

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Figure 2-57 gives a summary of the Mohr circles for Active and Passive failure of a cohesion less soil.

Screen Shot 2020-08-15 at 1.52.27 PM.png — Figure 2-57: The Mohr circles for active and passive failure for a cohesion less soil.

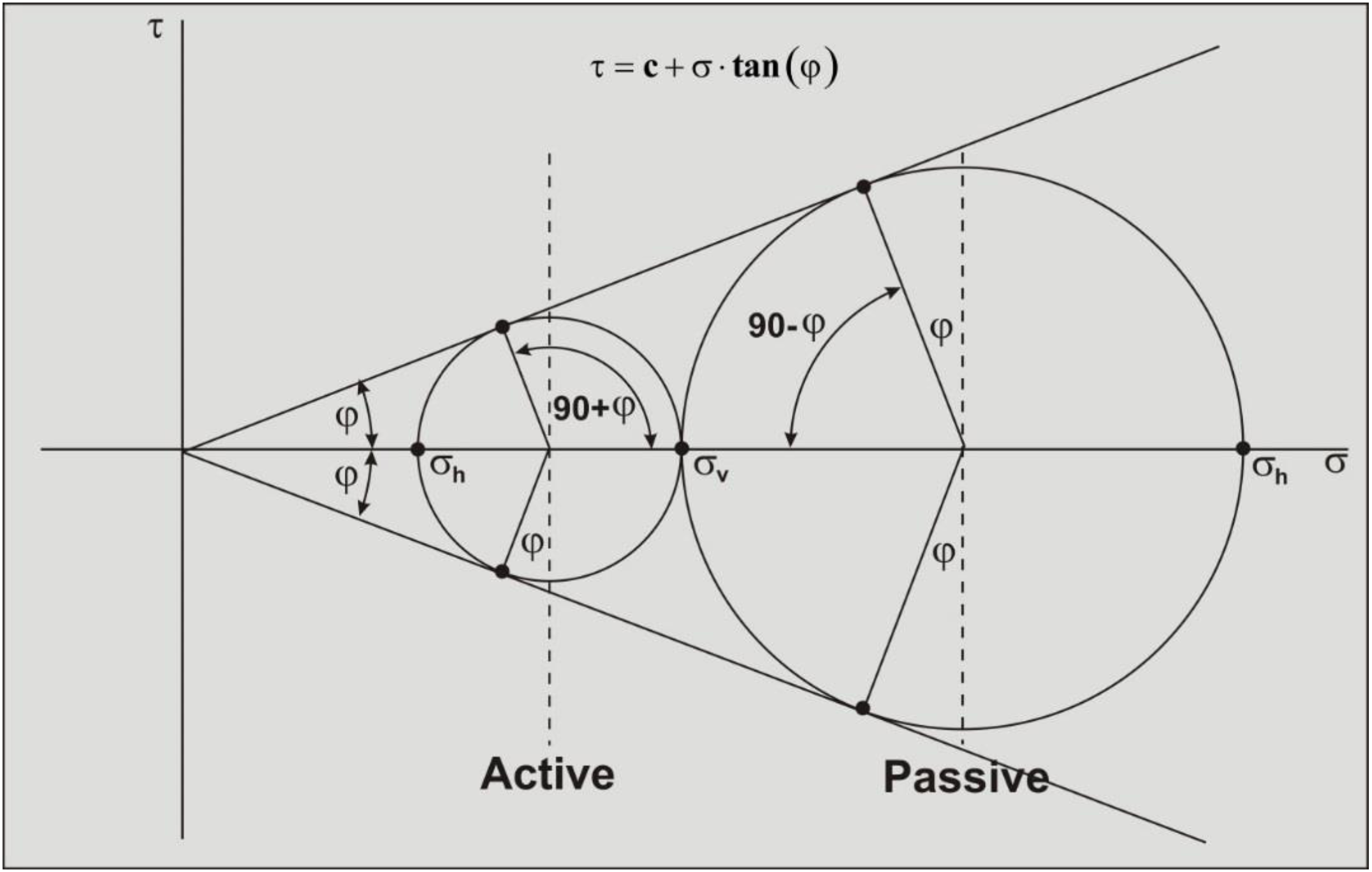
Some equations for a cohesion less soil in the active state:

Failure will occur if:

\[\ \sin (\varphi)=\frac{\frac{1}{2} \cdot\left(\sigma_{\mathrm{v}}-\sigma_{\mathrm{h}}\right)}{\frac{1}{2} \cdot\left(\sigma_{\mathrm{v}}+\sigma_{\mathrm{h}}\right)}\tag{2-114}\]

This can also be written as:

\[\ \left(\frac{\sigma_{\mathrm{v}}-\sigma_{\mathrm{h}}}{2}\right)-\left(\frac{\sigma_{\mathrm{v}}+\sigma_{\mathrm{h}}}{2}\right) \cdot \sin (\varphi)=0\tag{2-115}\]

Using this equation the value of σ_h can be expressed into σ_v:

\[\ \sigma_{\mathrm{h}}=\sigma_{\mathrm{v}} \frac{1-\sin (\varphi)}{1+\sin (\varphi)}=\mathrm{K}_{\mathrm{a}} \cdot \sigma_{\mathrm{v}}\tag{2-116}\]

On the other hand, the value of σ_v can also be expressed into σ_h:

\[\ \sigma_{\mathrm{v}}=\sigma_{\mathrm{h}} \frac{1+\sin (\varphi)}{1-\sin (\varphi)}=\mathrm{K}_{\mathrm{p}} \cdot \sigma_{\mathrm{h}}\tag{2-117}\]

For the passive state the stresses σ_v and σ_h should be reversed.

Figure 2-58 gives a summary of the Mohr circles for Active and Passive failure for a soil with cohesion.

Screen Shot 2020-08-15 at 2.08.13 PM.png — Figure 2-58: The Mohr circles for active and passive failure for a soil with cohesion.

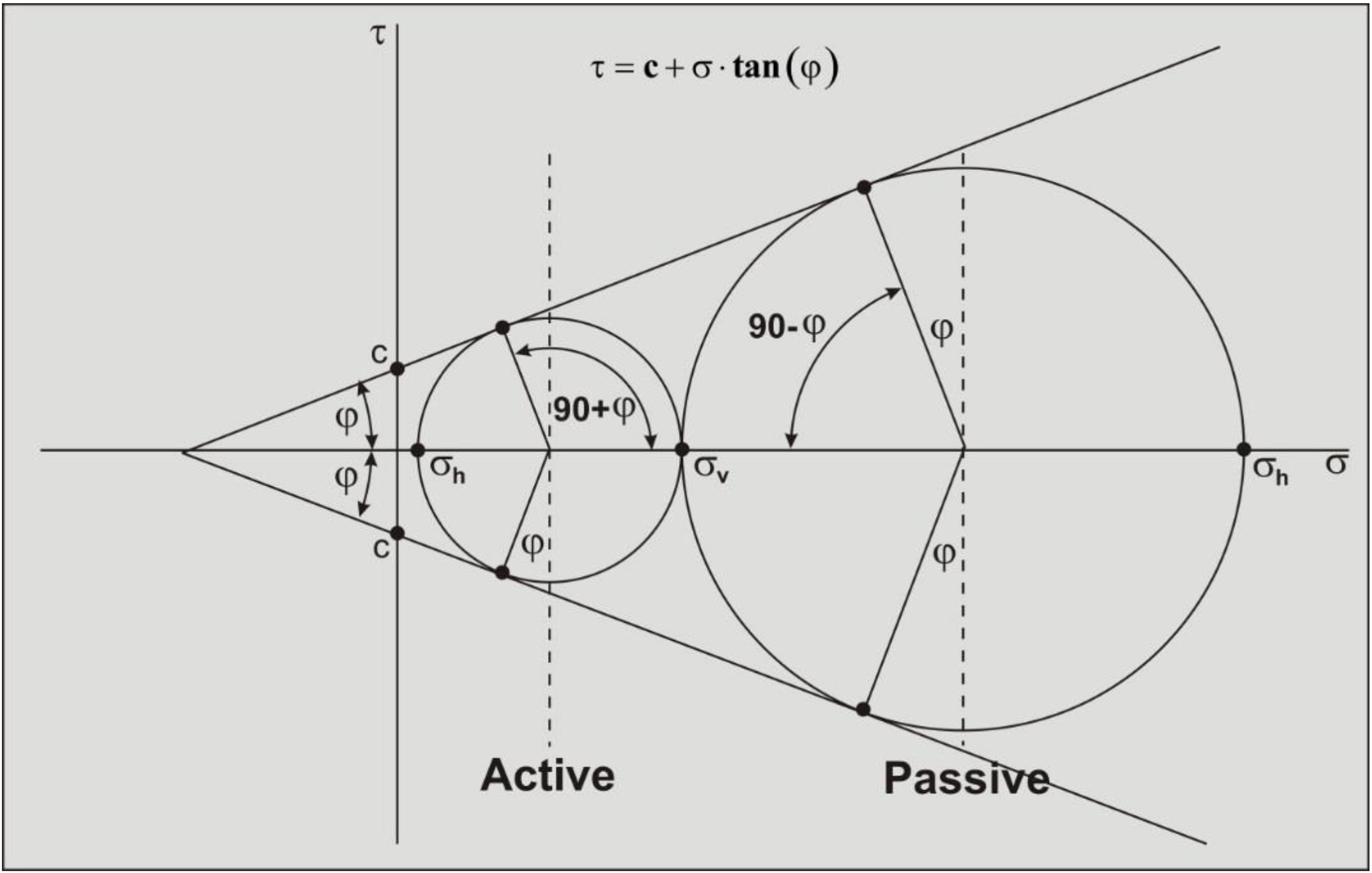
Some equations for a soil with cohesion in the active state:

Failure will occur if:

\[\ \sin (\varphi)=\frac{\frac{1}{2} \cdot\left(\sigma_{\mathrm{v}}-\sigma_{\mathrm{h}}\right)}{\mathrm{c} \cdot \cot (\varphi)+\frac{1}{2} \cdot\left(\sigma_{\mathrm{v}}+\sigma_{\mathrm{h}}\right)}\tag{2-118}\]

This can also be written as:

\[\ \left(\frac{\sigma_{\mathrm{v}}-\sigma_{\mathrm{h}}}{2}\right)-\left(\frac{\sigma_{\mathrm{v}}+\sigma_{\mathrm{h}}}{2}\right) \cdot \sin (\varphi)-\mathrm{c} \cdot \cos (\varphi)=0\tag{2-119}\]

Using this equation the value of σ_h can be expressed into σ_v:

\[\ \sigma_{\mathrm{h}}=\sigma_{\mathrm{v}} \frac{1-\sin (\varphi)}{1+\sin (\varphi)}-2 \cdot \mathrm{c} \cdot \frac{\cos (\varphi)}{1+\sin (\varphi)}=\mathrm{K}_{\mathrm{a}} \cdot \sigma_{\mathrm{v}}-2 \cdot \mathrm{c} \cdot \sqrt{\mathrm{K}_{\mathrm{a}}}\tag{2-120}\]

On the other hand, the value of σ_v can also be expressed into σ_h:

\[\ \sigma_{\mathrm{v}}=\sigma_{\mathrm{h}} \frac{1+\sin (\varphi)}{1-\sin (\varphi)}+2 \cdot \mathrm{c} \cdot \frac{\cos (\varphi)}{1-\sin (\varphi)}=\mathrm{K}_{\mathrm{p}} \cdot \sigma_{\mathrm{h}}+2 \cdot \mathrm{c} \cdot \sqrt{\mathrm{K}_{\mathrm{p}}}\tag{2-121}\]

For the passive state the stresses σ_v and σ_h should be reversed.