2.12: Shear Strength versus Friction
- Page ID
- 33354
To avoid confusion between cohesion and adhesion on one side and internal and external friction on the other side, internal and external friction, also named Coulomb friction, depend linearly on normal stresses, internal friction depends on the normal stress between the sand grains and external friction on the normal stress between the sand grains and another material, for example steel. In civil engineering internal and external friction are denoted by the angle of internal friction and the angle of external friction, also named the soil/interface friction angle. In mechanical engineering the internal and external friction angles are denoted by the internal and external friction coefficient. If there is no normal stress, there is no shear stress resulting from normal stress, so the friction is zero. Adhesion and cohesion are considered to be the sticky effect between two surfaces. Cohesion is the sticky effect between two surfaces of the same material before any failure has occurred and adhesion is the sticky effect between two different materials, for example adhesive tape. Adhesion and cohesion could be named the external and internal shear strength which are independent from normal stresses. The equations for the resulting shear stresses are:
\[\ \tau_{\mathrm{in}}=\tau_{\mathrm{c}}+\sigma_{\mathrm{in}} \cdot \tan (\varphi) \quad\text{ or }\quad \tau_{\mathrm{in}}=\tau_{\mathrm{c}}+\sigma_{\mathrm{in}} \cdot \mu_{\mathrm{in}}\tag{2-122}\]
\[\ \tau_{\mathrm{ex}}=\tau_{\mathrm{a}}+\sigma_{\mathrm{ex}} \cdot \tan (\delta) \quad\text{ or }\quad \tau_{\mathrm{ex}}=\tau_{\mathrm{a}}+\sigma_{\mathrm{ex}} \cdot \mu_{\mathrm{ex}}\tag{2-123}\]
Or
\[\ \mathrm{\tau_{\mathrm{in}}=c+\sigma_{\mathrm{in}} \cdot \tan (\varphi) \quad\text{ or }\quad \tau_{\mathrm{in}}=c+\sigma_{\mathrm{in}} \cdot \mu_{\mathrm{in}}}\tag{2-124}\]
\[\ \tau_{\mathrm{ex}}=\mathrm{a}+\sigma_{\mathrm{ex}} \cdot \tan (\delta) \quad\text{ or }\quad \tau_{\mathrm{ex}}=\mathrm{a}+\sigma_{\mathrm{ex}} \cdot \mu_{\mathrm{ex}}\tag{2-125}\]
With:
\[\ \mu_{\mathrm{in}}=\tan (\varphi)\tag{2-126}\]
\[\ \mu_{\mathrm{ex}}=\tan (\delta)\tag{2-127}\]
The values of the internal friction angle φ and the external friction angle δ not only depend on the soil properties like the density and the shape of the particles, but may also depend on the deformation history.
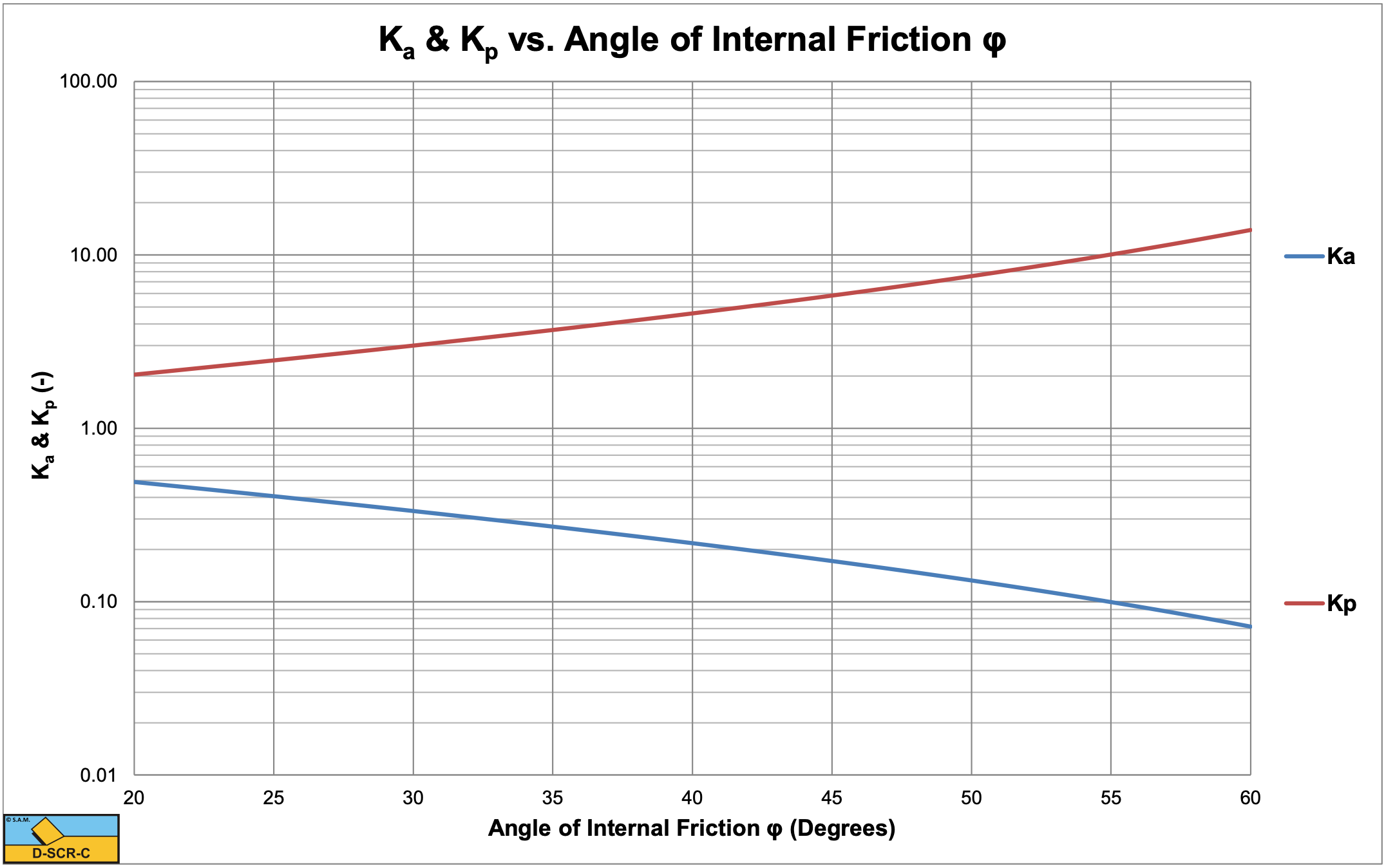
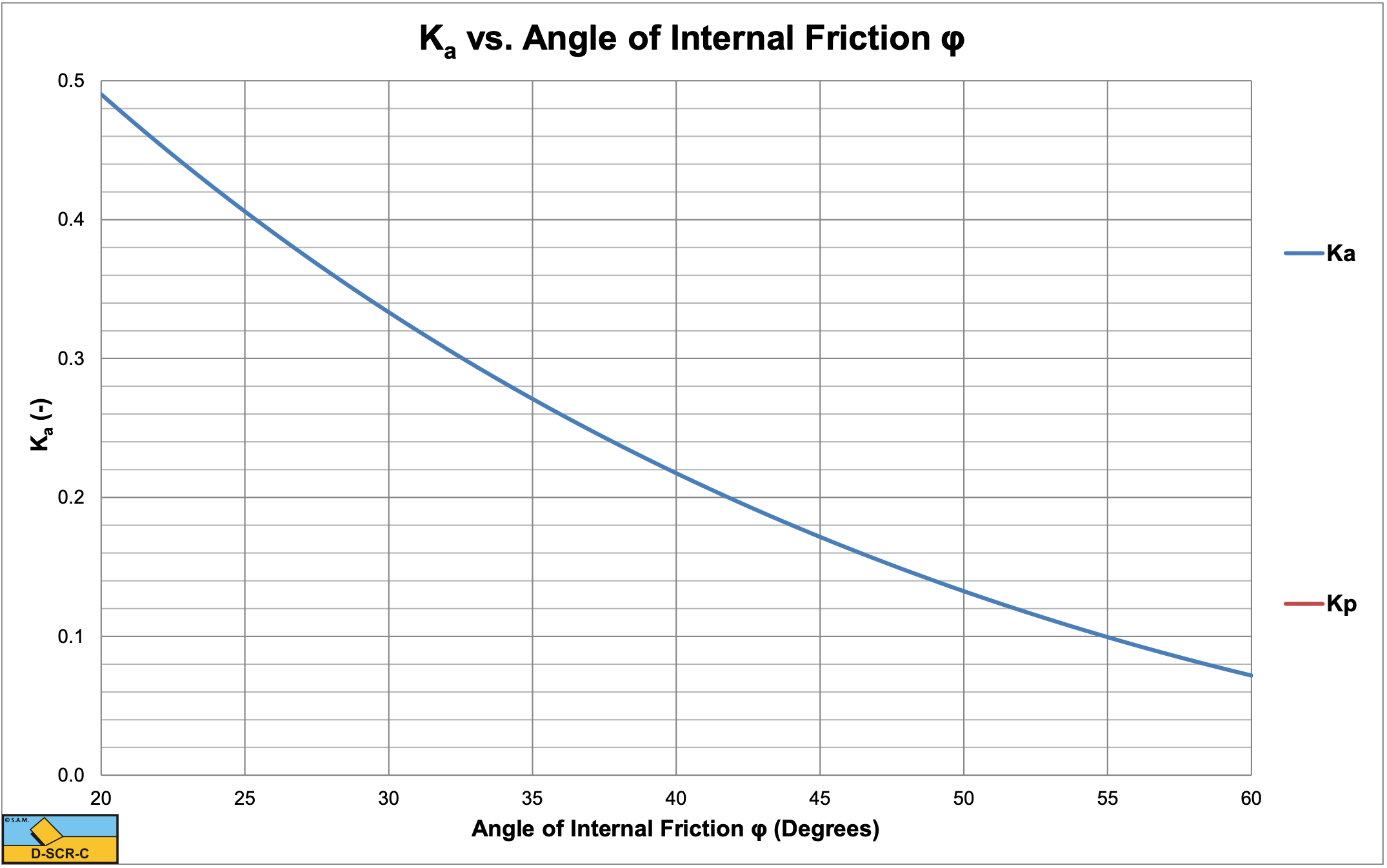
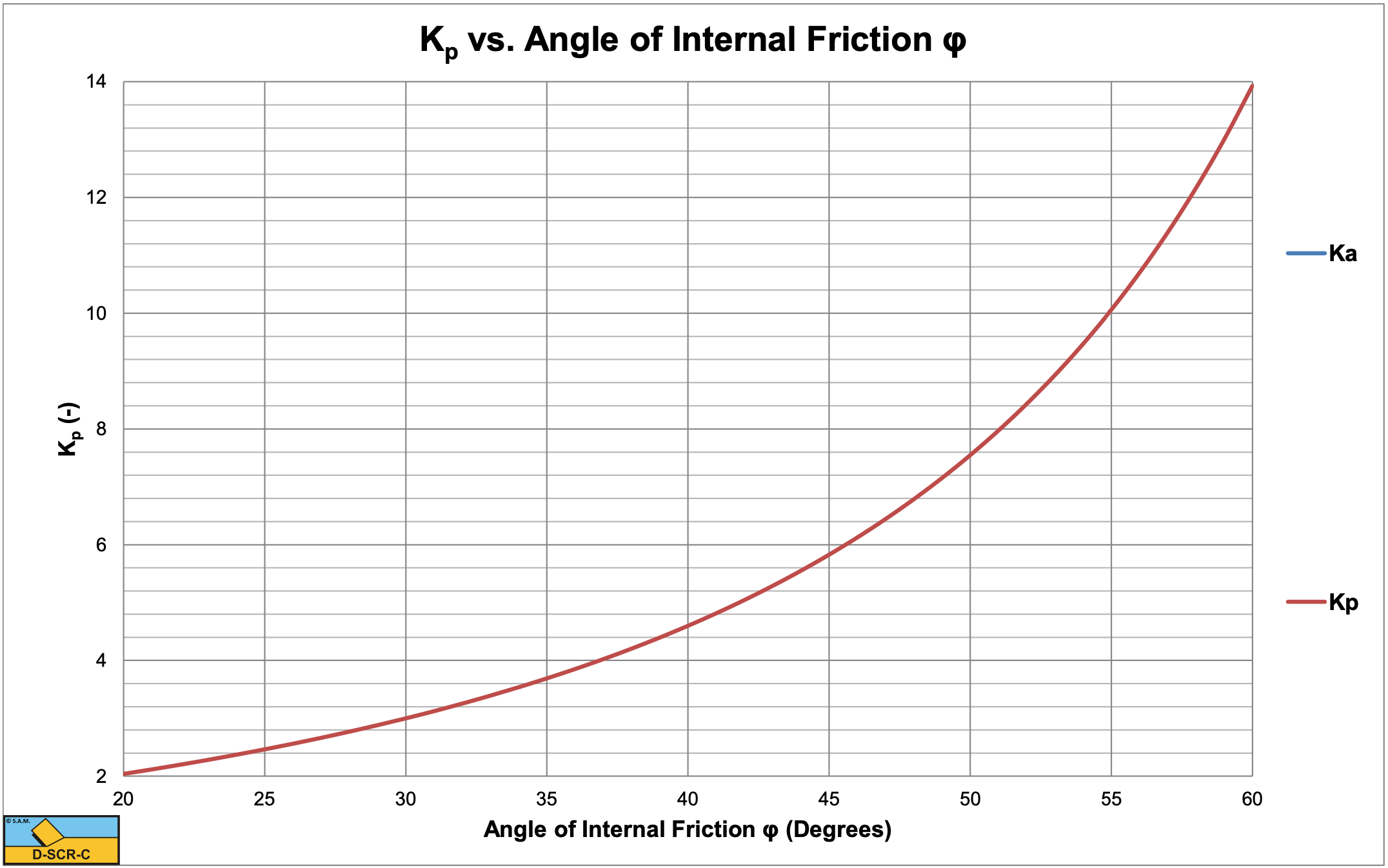
Figure 2-59, Figure 2-60 and Figure 2-61 show the Ka and Kp coefficients as a function of the internal friction angle.