3.3: The Flow, Shear, and Crushed Type
- Page ID
- 29431
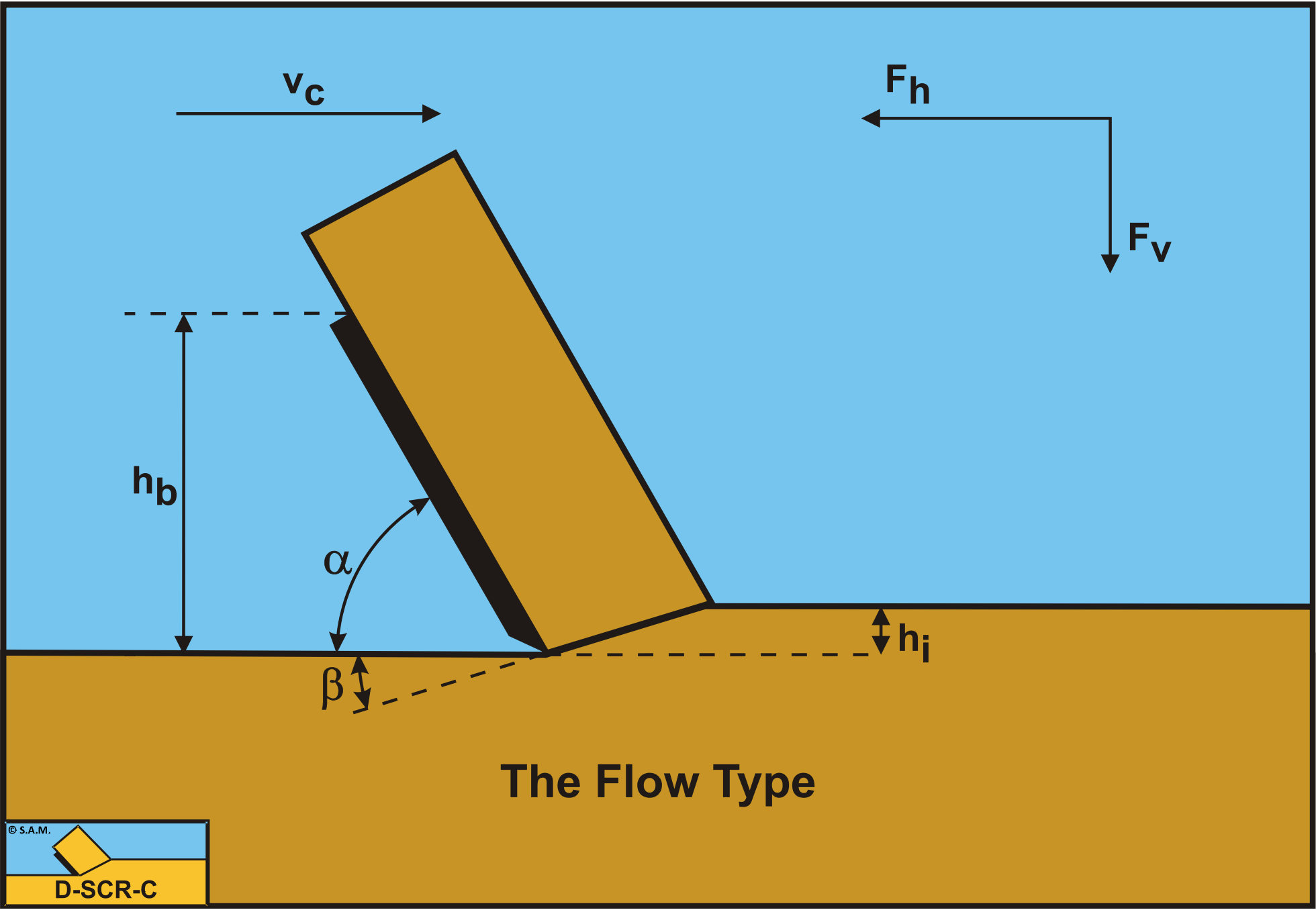
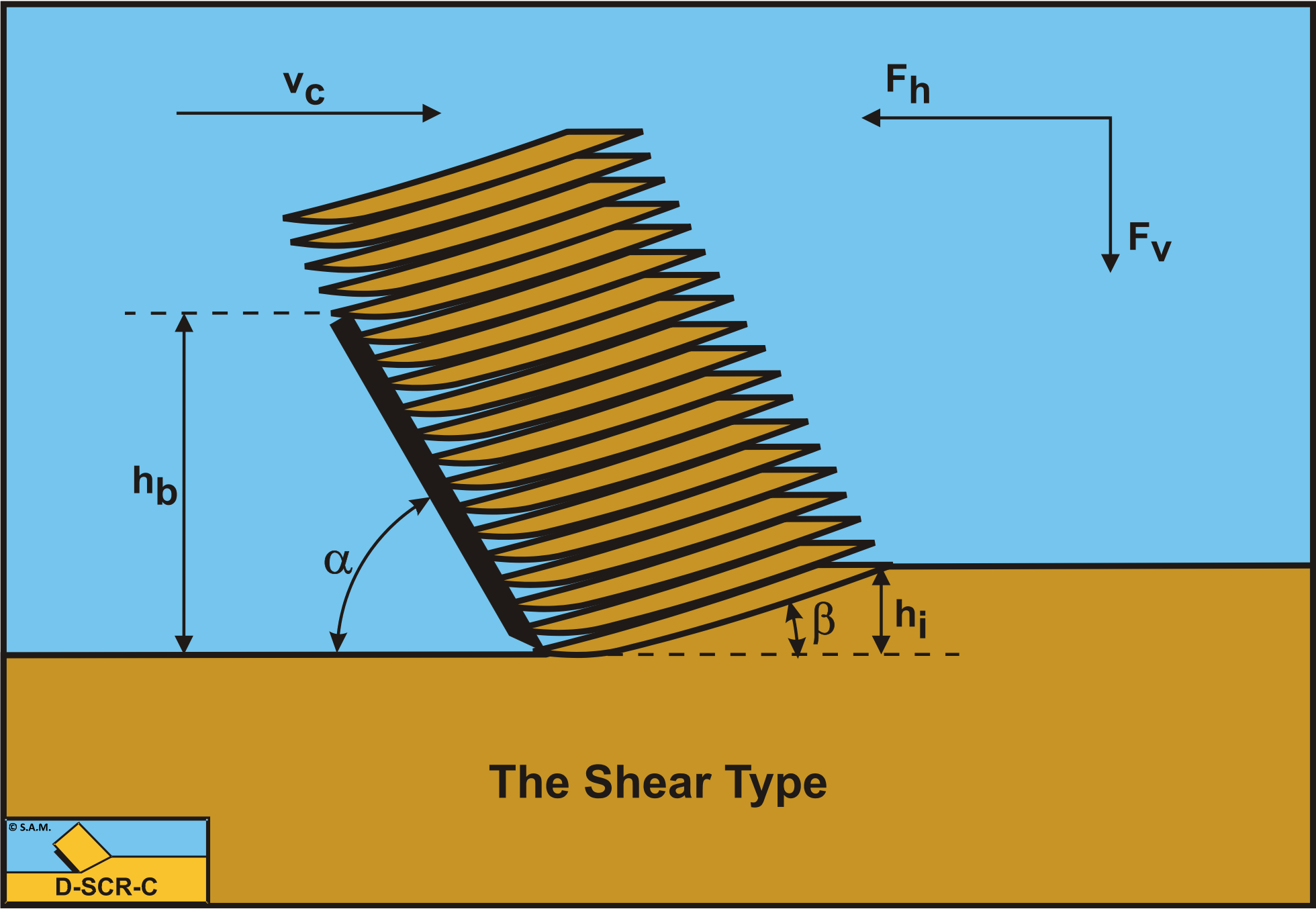
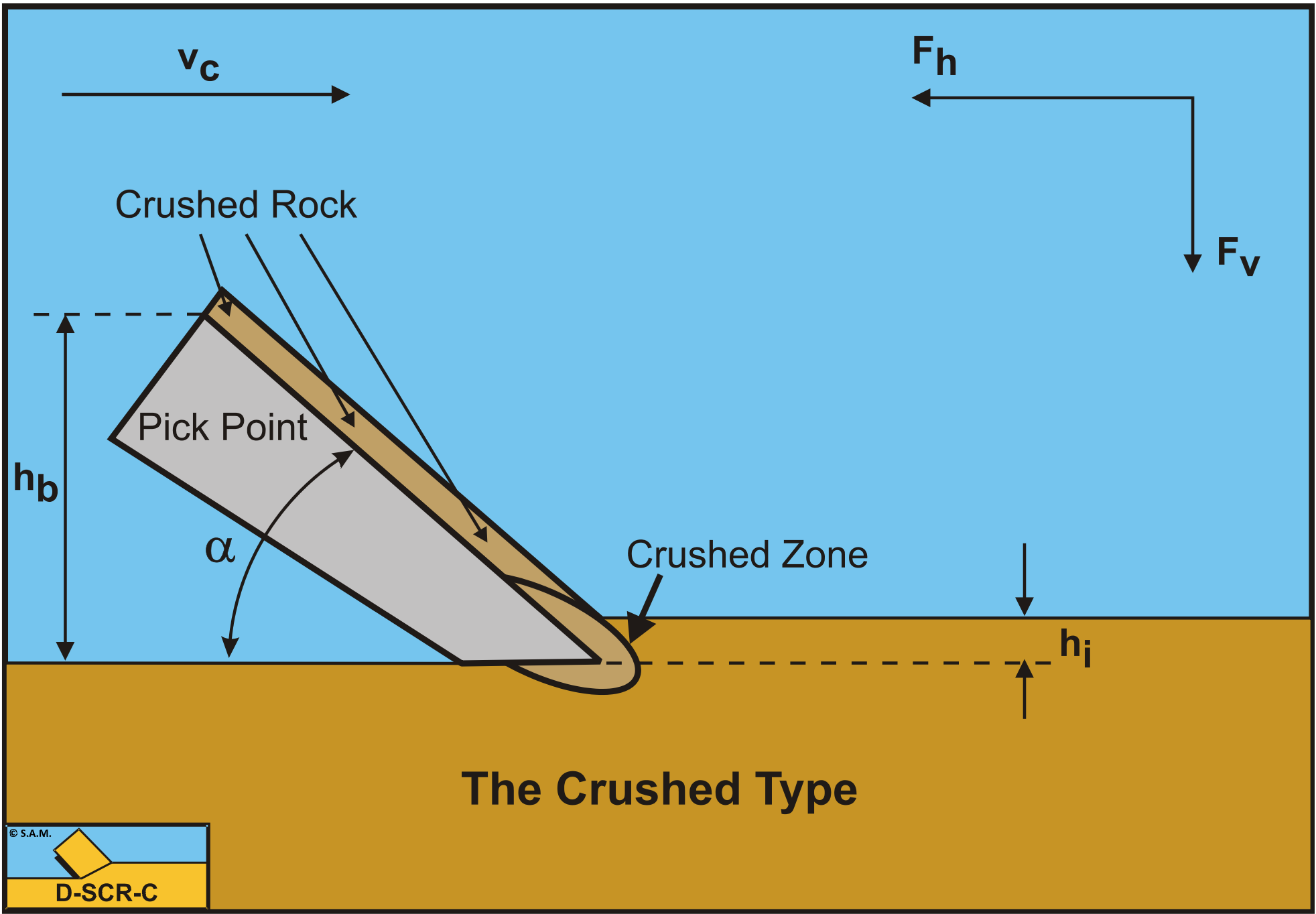
Figure 3-3 and Figure 3-4 show the Flow Type and the Shear Type of cutting process. The Shear Type is modeled as the Flow Type. The difference is that in dry soil the forces calculated for the Flow Type are constant forces because the process is ductile. For the Shear Type the forces are the peak forces, because the process is assumed to be brittle (shear). The average forces can be determined by multiplying the peak forces with a factor of 1⁄4 to 1⁄2.
3.3.1. The Equilibrium of Forces
Figure 3-6 illustrates the forces on the layer of soil cut. The forces shown are valid in general. The forces acting on this layer are:
-
A normal force acting on the shear surface N1 resulting from the effective grain stresses.
-
A shear force S1 as a result of internal friction N1·tan(φ).
-
A force W1 as a result of water under pressure in the shear zone.
-
A shear force C as a result of pure cohesion \(\ \tau_\mathrm{c}\). This force can be calculated by multiplying the cohesive shear strength \(\ \tau_\mathrm{c}\) with the area of the shear plane.
-
A gravity force G as a result of the (under water) weight of the layer cut.
-
An inertial force I, resulting from acceleration of the soil.
-
A force normal to the blade N2, resulting from the effective grain stresses.
-
A shear force S2 as a result of the external friction angle N2·tan(δ).
-
A shear force A as a result of pure adhesion between the soil and the blade \(\ \tau_\mathrm{a}\). This force can be calculated by multiplying the adhesive shear strength \(\ \tau_\mathrm{a}\) of the soil with the contact area between the soil and the blade.
-
A force W2 as a result of water under pressure on the blade
The normal force N1 and the shear force S1 can be combined to a resulting grain force K1.
\[\ \mathrm{K}_{1}=\sqrt{\mathrm{N}_{\mathrm{1}}^{\mathrm{2}}+\mathrm{S}_{\mathrm{1}}^{\mathrm{2}}}\tag{3-2}\]
The forces acting on a straight blade when cutting soil, can be distinguished as:
-
A force normal to the blade N2, resulting from the effective grain stresses.
-
A shear force S2 as a result of the external friction angle N2·tan(δ).
-
A shear force A as a result of pure adhesion between the soil and the blade \(\ \tau_\mathrm{a}\). This force can be calculated by multiplying the adhesive shear strength \(\ \tau_\mathrm{a}\) of the soil with the contact area between the soil and the blade.
-
A force W2 as a result of water under pressure on the blade.
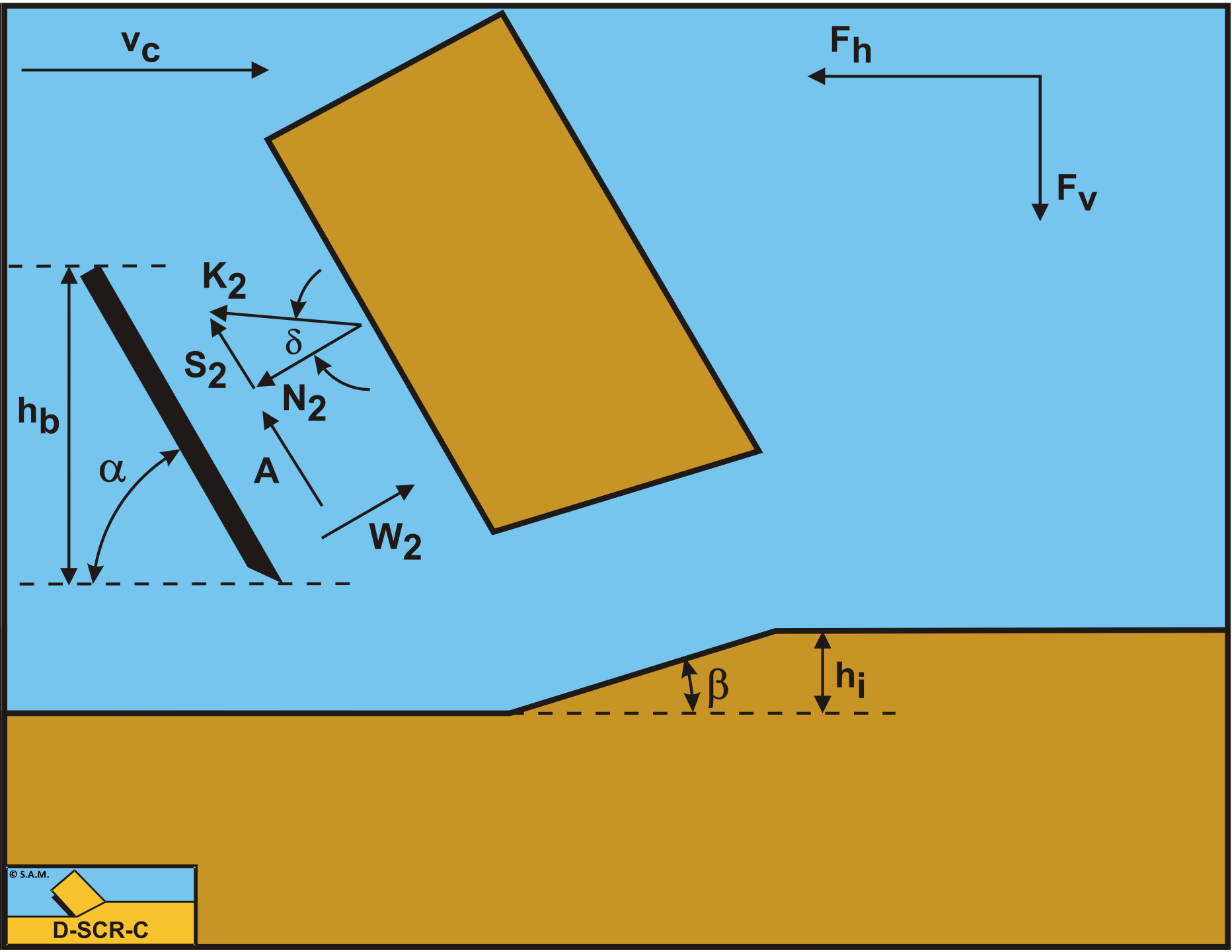
These forces are shown in Figure 3-7. If the forces N2 and S2 are combined to a resulting force K2 and the adhesive force A and the water under pressures forces W1 and W2 are known, then the resulting force K2 is the unknown force on the blade. By taking the horizontal and vertical equilibrium of forces an expression for the force K2 on the blade can be derived.
\[\ \mathrm{K}_{2}=\sqrt{\mathrm{N}_{2}^{2}+\mathrm{S}_{2}^{2}}\tag{3-3}\]
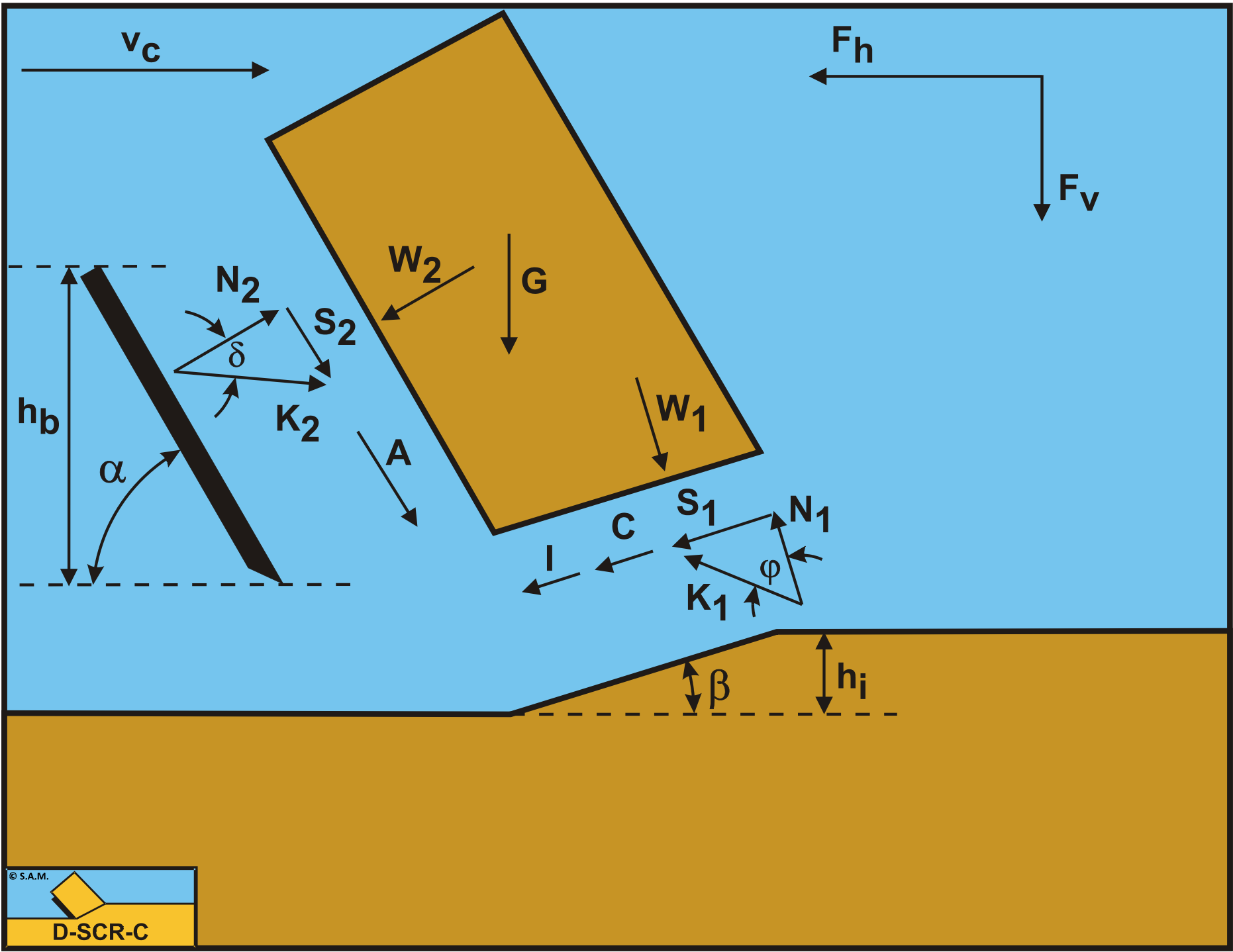
The horizontal equilibrium of forces:
\[\ \begin{array}{left} \sum \mathrm{F}_{\mathrm{h}}=& \mathrm{K}_{1} \cdot \sin (\beta+\varphi)-\mathrm{W}_{1} \cdot \sin (\beta)+\mathrm{C} \cdot \cos (\beta)+\mathrm{I} \cdot \cos (\beta) \\ &-\mathrm{A} \cdot \cos (\alpha)+\mathrm{W}_{2} \cdot \sin (\alpha)-\mathrm{K}_{2} \cdot \sin (\alpha+\delta)=0 \end{array}\tag{3-4}\]
The vertical equilibrium of forces:
\[\ \begin{array}{left} \sum \mathrm{F}_{\mathrm{v}}=&-\mathrm{K}_{\mathrm{1}} \cdot \cos (\boldsymbol{\beta}+\varphi)+\mathrm{W}_{\mathrm{1}} \cdot \cos (\boldsymbol{\beta})+\mathrm{C} \cdot \sin (\boldsymbol{\beta})+\mathrm{I} \cdot \sin (\boldsymbol{\beta}) \\ &+\mathrm{G}+\mathrm{A} \cdot \sin (\boldsymbol{\alpha})+\mathrm{W}_{\mathrm{2}} \cdot \mathrm{c o s}(\boldsymbol{\alpha})-\mathrm{K}_{2} \cdot \cos (\boldsymbol{\alpha}+\delta)=\mathrm{0} \end{array}\tag{3-5}\]
The force K1 on the shear plane is now:
\[\ \begin{array}{left} \mathrm{K}_{1}=& \frac{\mathrm{W}_{2} \cdot \sin (\delta)+\mathrm{W}_{1} \cdot \sin (\alpha+\beta+\delta)+\mathrm{G} \cdot \sin (\alpha+\delta)}{\sin (\alpha+\beta+\delta+\varphi)} \\ &+\frac{-\mathrm{I} \cdot \cos (\alpha+\beta+\delta)-\mathrm{C} \cdot \cos (\alpha+\beta+\delta)+\mathrm{A} \cdot \cos (\delta)}{\sin (\alpha+\beta+\delta+\varphi)} \end{array}\tag{3-6}\]
The force K2 on the blade is now:
\[\ \begin{array}{left} \mathrm{K}_{2}=& \frac{\mathrm{W}_{2} \cdot \sin (\alpha+\beta+\varphi)+\mathrm{W}_{1} \cdot \sin (\varphi)+\mathrm{G} \cdot \sin (\beta+\varphi)}{\sin (\alpha+\beta+\delta+\varphi)} \\ &+\frac{+\mathrm{I} \cdot \cos (\varphi)+\mathrm{C} \cdot \cos (\varphi)-\mathrm{A} \cdot \cos (\alpha+\beta+\varphi)}{\sin (\alpha+\beta+\delta+\varphi)} \end{array}\tag{3-7}\]
From equation (3-7) the forces on the blade can be derived. On the blade a force component in the direction of cutting velocity Fh and a force perpendicular to this direction Fv can be distinguished.
\[\ \mathrm{F_{h}=-W_{2} \cdot \sin (\alpha)+K_{2} \cdot \sin (\alpha+\delta)+A \cdot \cos (\alpha)}\tag{3-8}\]
\[\ \mathrm{F}_{v}=-\mathrm{W}_{2} \cdot \cos (\alpha)+\mathrm{K}_{2} \cdot \cos (\alpha+\delta)-\mathrm{A} \cdot \sin (\alpha)\tag{3-9}\]
The normal force on the shear plane is now:
\[\ \begin{array}{left} \mathrm{N}_{1}=& \frac{\mathrm{W}_{2} \cdot \sin (\delta)+\mathrm{W}_{1} \cdot \sin (\alpha+\beta+\delta)+\mathrm{G} \cdot \sin (\alpha+\delta)}{\sin (\alpha+\beta+\delta+\varphi)} \cdot \cos (\varphi) \\ &+\frac{-\mathrm{I} \cdot \cos (\alpha+\beta+\delta)-\mathrm{C} \cdot \cos (\alpha+\beta+\delta)+\mathrm{A} \cdot \cos (\delta)}{\sin (\alpha+\beta+\delta+\varphi)} \cdot \cos (\varphi) \end{array}\tag{3-10}\]
The normal force on the blade is now:
\[\ \begin{array}{left} \mathrm{N}_{2}=& \frac{\mathrm{W}_{2} \cdot \sin (\alpha+\beta+\varphi)+\mathrm{W}_{1} \cdot \sin (\varphi)+\mathrm{G} \cdot \sin (\beta+\varphi)}{\sin (\alpha+\beta+\delta+\varphi)} \cdot \cos (\delta) \\ &+\frac{+\mathrm{I} \cdot \cos (\varphi)+\mathrm{C} \cdot \cos (\varphi)-\mathrm{A} \cdot \cos (\alpha+\beta+\varphi)}{\sin (\alpha+\beta+\delta+\varphi)} \cdot \cos (\delta) \end{array}\tag{3-11}\]
If the equations (3-10) and (3-11) give a positive result, the normal forces are compressive forces. It can be seen from these equations that the normal forces can become negative, meaning that a tensile rupture might occur, depending on values for the adhesion and cohesion and the angles involved. The most critical direction where this might occur can be found from the Mohr circle.
3.3.2. The Individual Forces
If there is no cavitation the water pressures forces W1 and W2 can be written as:
\[\ \mathrm{W}_{1}=\frac{\mathrm{p}_{1 \mathrm{m}} \cdot \rho_{\mathrm{w}} \cdot \mathrm{g} \cdot \mathrm{v}_{\mathrm{c}} \cdot \mathrm{\varepsilon} \cdot \mathrm{h}_{\mathrm{i}}^{2} \cdot \mathrm{w}}{\left(\mathrm{a}_{\mathrm{1}} \cdot \mathrm{k}_{\mathrm{i}}+\mathrm{a}_{\mathrm{2}} \cdot \mathrm{k}_{\mathrm{m a x}}\right) \cdot \sin (\beta)}=\frac{\mathrm{p}_{1 \mathrm{m}} \cdot \rho_{\mathrm{w}} \cdot \mathrm{g} \cdot \mathrm{v}_{\mathrm{c}} \cdot \varepsilon \cdot \mathrm{h}_{\mathrm{i}}^{2} \cdot \mathrm{w}}{\mathrm{k}_{\mathrm{m}} \cdot \sin (\beta)}\tag{3-12}\]
\[\ \mathrm{W}_{2}=\frac{\mathrm{p}_{2 \mathrm{m}} \cdot \rho_{\mathrm{w}} \cdot \mathrm{g} \cdot \mathrm{v}_{\mathrm{c}} \cdot \varepsilon \cdot \mathrm{h}_{\mathrm{i}} \cdot \mathrm{w}}{\left(\mathrm{a}_{\mathrm{1}} \cdot \mathrm{k}_{\mathrm{i}}+\mathrm{a}_{\mathrm{2}} \cdot \mathrm{k}_{\mathrm{m a x}}\right) \cdot \sin (\alpha)}=\frac{\mathrm{p}_{2 \mathrm{m}} \cdot \rho_{\mathrm{w}} \cdot \mathrm{g} \cdot \mathrm{v}_{\mathrm{c}} \cdot \varepsilon \cdot \mathrm{h}_{\mathrm{i}} \cdot \mathrm{w}}{\mathrm{k}_{\mathrm{m}} \cdot \sin (\alpha)}\tag{3-13}\]
In case of cavitation W1 and W2 become:
\[\ \mathrm{W}_{1}=\frac{\rho_{\mathrm{w}} \cdot \mathrm{g} \cdot(\mathrm{z}+\mathrm{1 0}) \cdot \mathrm{h}_{\mathrm{i}} \cdot \mathrm{w}}{\sin (\beta)}\tag{3-14}\]
\[\ \mathrm{W}_{2}=\frac{\rho_{\mathrm{w}} \cdot \mathrm{g} \cdot(\mathrm{z}+\mathrm{1 0}) \cdot \mathrm{h}_{\mathrm{b}} \cdot \mathrm{w}}{\sin (\mathrm{\alpha})}\tag{3-15}\]
Wismer and Luth (1972A) and (1972B) investigated the inertia forces term I of the total cutting forces. The following equation is derived:
\[\ \mathrm{I}=\rho_{\mathrm{s}} \cdot \mathrm{v}_{\mathrm{c}}^{\mathrm{2}} \cdot \frac{\sin (\alpha)}{\sin (\alpha+\beta)} \cdot \mathrm{h}_{\mathrm{i}} \cdot \mathrm{w}\tag{3-16}\]
The cohesive and adhesive forces C and A can be determined with soil mechanical experiments. For the cohesive and adhesive forces the following equations are valid:
\[\ \mathrm{C=\frac{c \cdot h_{i} \cdot w}{\sin (\beta)}}\tag{3-17}\]
\[\ \mathrm{A}=\frac{\mathrm{a} \cdot \mathrm{h}_{\mathrm{b}} \cdot \mathrm{w}}{\sin (\alpha)}\tag{3-18}\]
The gravitational force G (weight submerged) follows from:
\[\ \mathrm{G}=\left(\rho_{\mathrm{s}}-\rho_{\mathrm{w}}\right) \cdot \mathrm{g} \cdot \mathrm{h}_{\mathrm{i}} \cdot \mathrm{w} \cdot \frac{\sin (\alpha+\beta)}{\sin (\beta)} \cdot\left\{\frac{\left(\mathrm{h}_{\mathrm{b}}+\mathrm{h}_{\mathrm{i}} \cdot \sin (\alpha)\right)}{\sin (\alpha)}+\frac{\mathrm{h}_{\mathrm{i}} \cdot \cos (\alpha+\beta)}{2 \cdot \sin (\beta)}\right\}\tag{3-19}\]
The gravitational force G (dry weight) follows from:
\[\ \mathrm{G}=\rho_{\mathrm{s}} \cdot \mathrm{g} \cdot \mathrm{h}_{\mathrm{i}} \cdot \mathrm{w} \cdot \frac{\sin (\alpha+\beta)}{\sin (\beta)} \cdot\left\{\frac{\left(\mathrm{h}_{\mathrm{b}}+\mathrm{h}_{\mathrm{i}} \cdot \sin (\alpha)\right)}{\sin (\alpha)}+\frac{\mathrm{h}_{\mathrm{i}} \cdot \cos (\alpha+\beta)}{2 \cdot \sin (\beta)}\right\}\tag{3-20}\]
This is in accordance with the area that is used for the water pore pressure calculations in the case of water saturated sand (see Figure 6-7).


