4.4: Cutting Rock Atmospheric

Last updated
Save as PDF

Page ID: 29439

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Rock is the collection of materials where the grains are bonded chemically from very stiff clay, sandstone to very hard basalt. It is difficult to give one definition of rock or stone and also the composition of the material can differ strongly. Still it is interesting to see if the model used for sand and clay, which is based on the Coulomb model, can be used for rock as well. Typical parameters for rock are the compressive strength UCS and the tensile strength BTS and specifically the ratio between those two, which is a measure for how fractured the rock is. Rock also has shear strength and because it consists of bonded grains it will have an internal friction angle and an external friction angle. It can be assumed that the permeability of the rock is very low, so initially the pore pressures do no play a role under atmospheric conditions. Since the absolute hydrostatic pressure, which would result in a cavitation under pressure of the same magnitude can be neglected with respect to the compressive strength of the rock; the pore pressures are usually neglected. This results in a material where gravity, inertia, pore pressures and adhesion can be neglected.

Rock cutting under atmospheric conditions (normal dredging) is dominated by the internal shear strength and by the internal and external friction angles. The main cutting mechanism is the Chip Type, brittle cutting. Cutting a very thin layer or using large blade angles may result in the Crushed Type. This is covered in Chapter 8: Rock Cutting: Atmospheric Conditions.

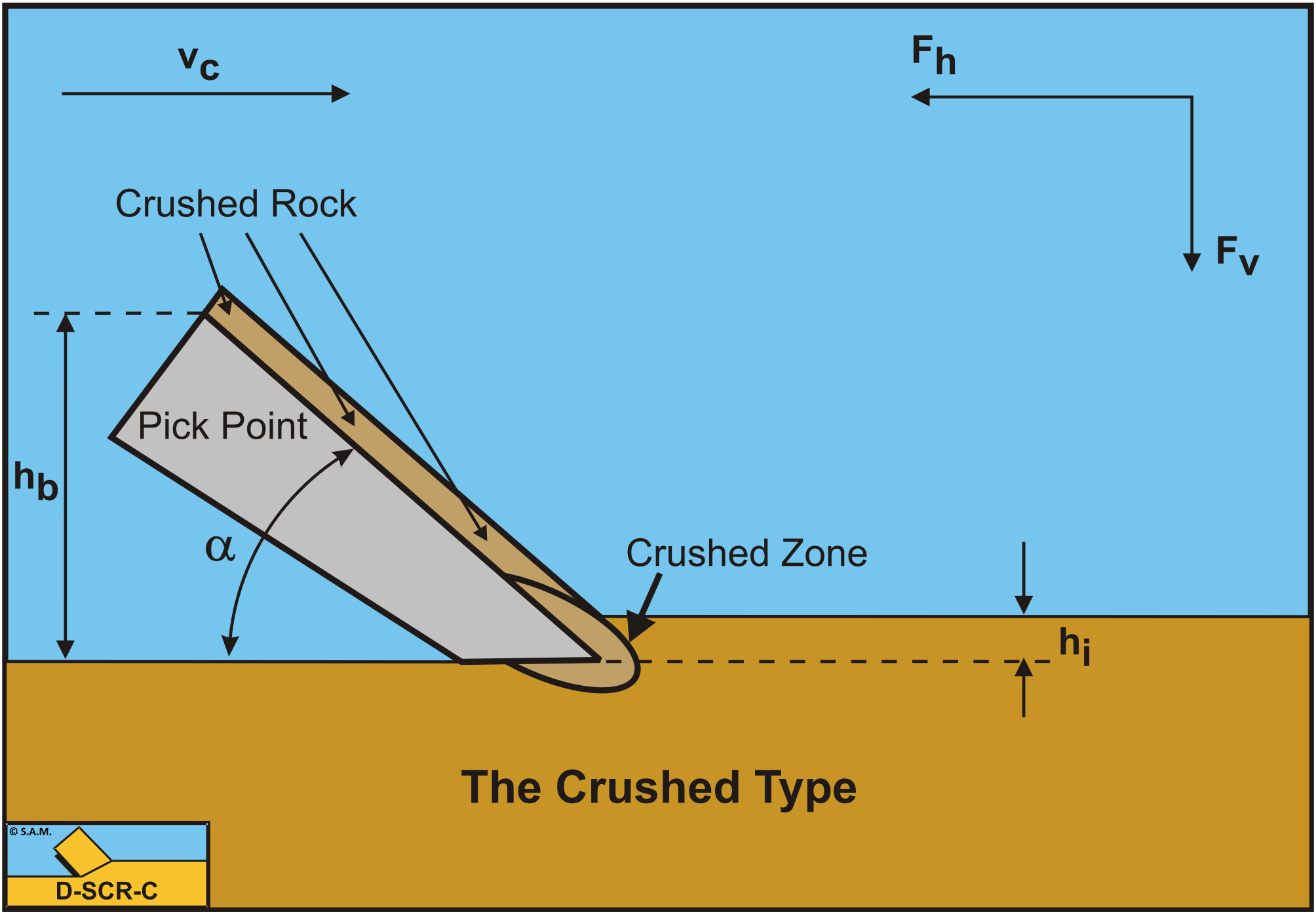
Screen Shot 2020-08-17 at 11.44.20 AM.png — Figure 4-6: The Crushed Type in atmospheric rock cutting.

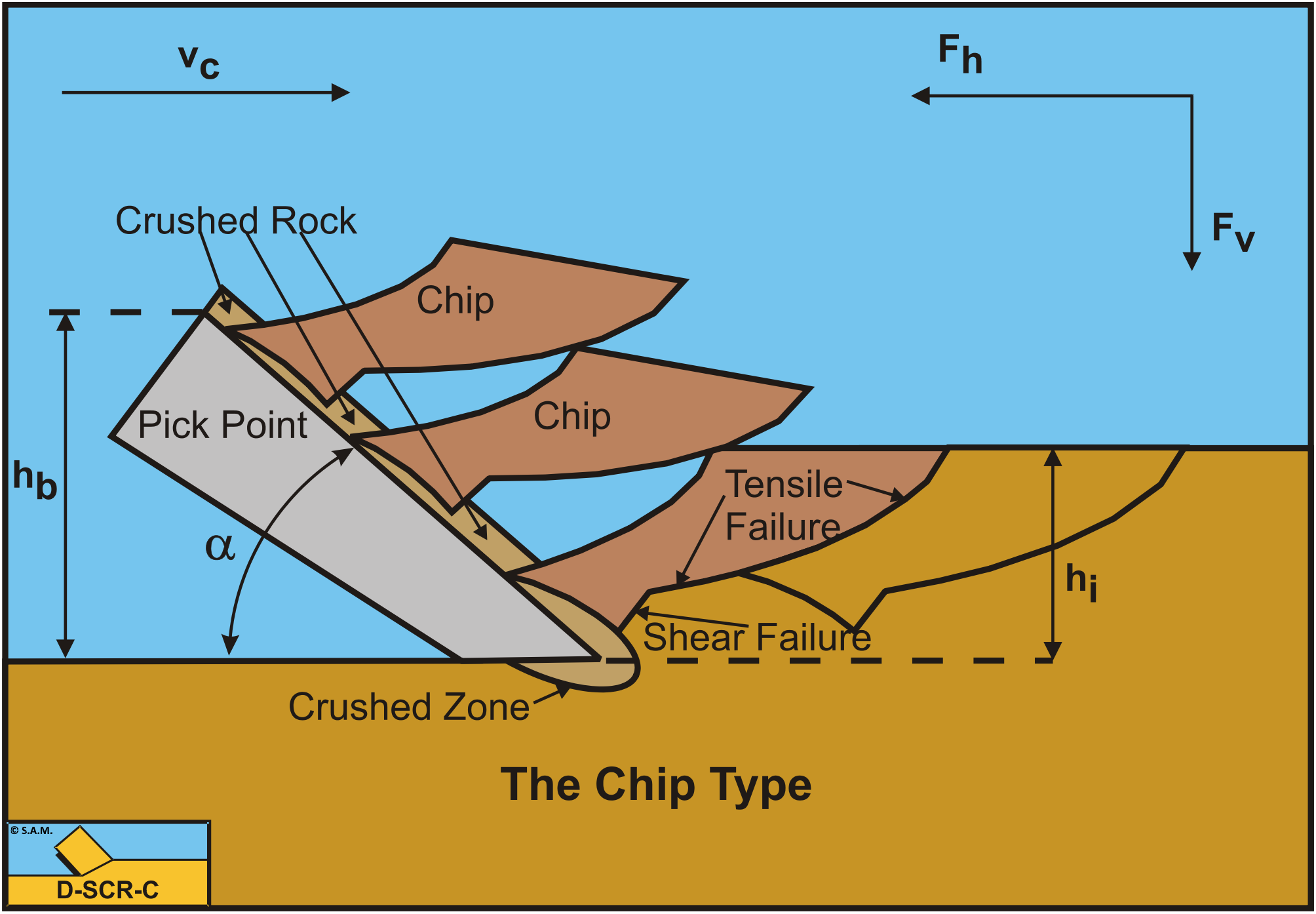
Screen Shot 2020-08-17 at 11.45.02 AM.png — Figure 4-7: The Chip Type in atmospheric rock cutting.

The forces K₁ and K₂ on the blade, chisel or pick point are now:

\[\ \begin{aligned} \mathrm{K}_{1}=& \frac{\mathrm{W}_{2} \cdot \sin (\delta)+\mathrm{W}_{1} \cdot \sin (\alpha+\beta+\delta)+\mathrm{G} \cdot \sin (\alpha+\delta)}{\sin (\alpha+\beta+\delta+\varphi)} \\ &+\frac{-\mathrm{I} \cdot \cos (\alpha+\beta+\delta)-\mathrm{C} \cdot \cos (\alpha+\beta+\delta)+\mathrm{A} \cdot \cos (\delta)}{\sin (\alpha+\beta+\delta+\varphi)} \end{aligned}\tag{4-19}\]

\[\ \begin{array}{left} \mathrm{K}_{2}=& \frac{\mathrm{W}_{2} \cdot \sin (\alpha+\beta+\varphi)+\mathrm{W}_{1} \cdot \sin (\varphi)+\mathrm{G} \cdot \sin (\beta+\varphi)}{\sin (\alpha+\beta+\delta+\varphi)} \\ &+\frac{+\mathrm{I} \cdot \cos (\varphi)+\mathrm{C} \cdot \cos (\varphi)-\mathrm{A} \cdot \cos (\alpha+\beta+\varphi)}{\sin (\alpha+\beta+\delta+\varphi)} \end{array}\tag{4-20}\]

The normal forces N₁ on the shear plane and N₂ on the blade are:

\[\ \mathrm{N}_{\mathrm{1}}=\mathrm{K}_{1} \cdot \cos (\varphi) \quad\text{ and }\quad \mathrm{N}_{2}=\mathrm{K}_{2} \cdot \cos (\delta)\tag{4-21}\]

The horizontal and vertical forces on the blade, chisel or pick point are:

\[\ \mathrm{F}_{\mathrm{h}}=-\mathrm{W}_{\mathrm{2}} \cdot \sin (\alpha)+\mathrm{K}_{2} \cdot \sin (\alpha+\delta)+\mathrm{A} \cdot \cos (\alpha)\tag{4-22}\]

\[\ \mathrm{F}_{\mathrm{v}}=-\mathrm{W}_{2} \cdot \cos (\alpha)+\mathrm{K}_{2} \cdot \cos (\alpha+\delta)-\mathrm{A} \cdot \sin (\alpha)\tag{4-23}\]

The equilibrium of moments around the blade tip is:

\[\ \left(\mathrm{N}_{1}-\mathrm{W}_{1}\right) \cdot \mathrm{R}_{1}-\mathrm{G} \cdot \mathrm{R}_{3}=\left(\mathrm{N}_{2}-\mathrm{W}_{2}\right) \cdot \mathrm{R}_{2}\tag{4-24}\]

Analyzing these equations results in the following conclusions:

Since the argument in the cosine of the cohesive term in the force K₁ is always greater than 90 degrees, the cosine is negative and the term as a whole is positive. This results in positive forces on the blade, chisel or pick point and also positive normal forces. The minimum normal stress however equals the normal stress on the shear plane, minus about the radius of the Mohr circle. The result may be a negative minimum normal stress. If this negative minimum normal stress is smaller than the negative tensile strength, brittle tensile failure will occur. Otherwise brittle shear failure will occur. In both cases the forces calculated are peak forces. The average forces are somewhere between 50% and 100% of the peak forces.
On the blade the normal stresses are always high enough to avoid the occurrence of the Curling Type. In fact the forces on the blade do not depend on the length of the blade. The cohesive force on the shear plane however depends on the (mobilized) cohesion or shear strength, so the Tear Type, here named the Chip Type may occur.
When the argument of the sine in the denominator gets close to 180 degrees, the forces become very large. If the argument is greater than 180 degrees, the forces would become negative. Since both conditions will not happen in nature, nature will find another cutting mechanism, the wedge mechanism.