6.3: Cutting Theory Literature
- Page ID
- 29452
In the seventies extensive research is carried out on the forces that occur while cutting sand under water. A conclusive cutting theory has however not been published in this period. However qualitative relations have been derived by several researchers, with which the dependability of the cutting forces with the soil properties and the blade geometry are described (Joanknecht (1974), van Os (1977A), (1976) and (1977B)).
A process that has a lot of similarities with the cutting of sand as far as water pressure development is concerned, is the, with uniform velocity, forward moving breach. Meijer and van Os (1976) and Meijer (1981) and (1985) have transformed the storage equation for the, with the breach, forward moving coordinate system.
\[\ \left|\frac{\partial^{2} \mathrm{p}}{\partial \mathrm{x}^{2}}\right|+\left|\frac{\partial^{2} \mathrm{p}}{\partial \mathrm{y}^{2}}\right|=\frac{\rho_{\mathrm{w}} \cdot \mathrm{g} \cdot \mathrm{v}_{\mathrm{c}}}{\mathrm{k}} \cdot\left|\frac{\partial \mathrm{e}}{\partial \mathrm{x}}\right|-\frac{\rho_{\mathrm{w}} \cdot \mathrm{g}}{\mathrm{k}} \cdot\left|\frac{\partial \mathrm{e}}{\partial \mathrm{t}}\right|\tag{6-1}\]
In the case of a stationary process, the second term on the right is zero, resulting:
\[\ \left|\frac{\partial^{2} \mathrm{p}}{\partial \mathrm{x}^{2}}\right|+\left|\frac{\partial^{2} \mathrm{p}}{\partial \mathrm{y}^{2}}\right|=\frac{\rho_{\mathrm{w}} \cdot \mathrm{g} \cdot \mathrm{v}_{\mathrm{c}}}{\mathrm{k}} \cdot\left|\frac{\partial \mathrm{e}}{\partial \mathrm{x}}\right|\tag{6-2}\]
Van Os (1977A), (1976) and (1977B) describes the basic principles of the cutting process, with special attention for the determination of the water sub-pressures and the cavitation. Van Os uses the non-transformed storage equation for the determination of the water sub-pressures.
\[\ \left|\frac{\partial^{2} \mathrm{p}}{\partial \mathrm{x}^{2}}\right|+\left|\frac{\partial^{2} \mathrm{p}}{\partial \mathrm{y}^{2}}\right|=\frac{\rho_{\mathrm{w}} \cdot \mathrm{g}}{\mathrm{k}} \cdot\left|\frac{\partial \mathrm{e}}{\partial \mathrm{t}}\right|\tag{6-3}\]
The average volume strain rate has to be substituted in the term \(\ \partial_\mathrm{e}/\partial_\mathrm{t}\) on the right. The average volume strain rate is the product of the average volume strain of the sand package and the cutting velocity and arises from the volume balance over the shear zone. Van Os gives a qualitative relation between the water sub-pressures and the average volume strain rate:
\[\ \mathrm{p}:: \frac{\mathrm{v}_{\mathrm{c}} \cdot \mathrm{h}_{\mathrm{i}} \cdot \varepsilon}{\mathrm{k}}\tag{6-4}\]
The problem of the solution of the storage equation for the cutting of sand under water is a mixed boundary value problem, for which the water sub-pressures along the boundaries are known (hydrostatic).
Joanknecht (1973) and (1974) assumes that the cutting forces are determined by the sub-pressure in the sand package. A distinction is made between the parts of the cutting force caused by the inertia forces, the sub-pressure behind the blade and the soil mechanical properties of the sand. The influence of the geometrical parameters gives the following qualitative relation:
\[\ \mathrm{F}_{\mathrm{c i}}:: \mathrm{v}_{\mathrm{c}} \cdot \mathrm{h}_{\mathrm{i}}^{\mathrm{2}} \cdot \mathrm{w}\tag{6-5}\]
The cutting force is proportional to the cutting velocity, the blade width and the square of the initial layer-thickness. A relation with the pore percentage and the permeability is also mentioned. A relation between the cutting force and these soil mechanical properties is however not given. It is observed that the cutting forces increase with an increasing blade angle.
In the eighties research has led to more quantitative relations. Van Leussen and Nieuwenhuis (1984) discuss the soil mechanical aspects of the cutting process. The forces models of Miedema (1984B), (1985B), (1985A), (1986B) and (1987 September), Steeghs (1985A) and (1985B) and the CSB (Combinatie Speurwerk Baggertechniek) model (van Leussen and van Os (1987 December)) are published in the eighties.
Brakel (1981) derives a relation for the determination of the water sub-pressures based upon, over each other rolling, round grains in the shear zone. The force part resulting from this is added to the model of Hettiaratchi and Reece (1974).
Miedema (1984B) has combined the qualitative relations of Joanknecht (1973) and (1974) and van Os (1976), (1977A) and (1977B) to the following relation:
\[\ \mathrm{F}_{\mathrm{ci}}:: \frac{\rho_{\mathrm{w}} \cdot \mathrm{g} \cdot \mathrm{v}_{\mathrm{c}} \cdot \mathrm{h}_{\mathrm{i}}^{2} \cdot \mathrm{w} \cdot \mathrm{\varepsilon}}{\mathrm{k}_{\mathrm{m}}}\tag{6-6}\]
With this basic equation calculation models are developed for a cutter head and for the periodical moving cutter head in the breach. The proportionality constants are determined empirically.
Van Leussen and Nieuwenhuis (1984) discuss the soil mechanical aspects of the cutting process. Important in the cutting process is the way shear takes place and the shape or angle of the shear plane, respectively shear zone. In literature no unambiguous image could be found. Cutting tests along a windowpane gave an image in which the shape of the shear plane was more in accordance with the so-called "stress characteristics" than with the so-called "zero-extension lines". Therefore, for the calculation of the cutting forces, the "stress characteristics method" is used (Mohr-Coulomb failure criterion). For the calculation of the water sub-pressures, however, the "zero- extension lines" are used, which are lines with a zero linear strain. A closer description has not been given for both calculations.
Although the cutting process is considered as being two-dimensional, Van Leussen and Nieuwenhuis found, that the angle of internal friction, measured at low deformation rates in a tri-axial apparatus, proved to be sufficient for dredging processes. Although the cutting process can be considered as a two-dimensional process and therefore it should be expected that the angle of internal friction has to be determined with a "plane deformation test". A sufficient explanation has not been found.
Little is known about the value of the angle of friction between sand and steel. Van Leussen and Nieuwenhuis don't give an unambiguous method to determine this soil mechanical parameter. It is, however, remarked that at low cutting velocities (0.05 mm/s), the soil/steel angle of friction can have a statistical value which is 1.5 to 2 times larger than the dynamic soil/steel angle of friction. The influence of the initial density on the resulting angle of friction is not clearly present, because loosely packed sand moves over the blade. The angles of friction measured on the blades are much larger than the angles of friction measured with an adhesion cell, while also a dependency with the blade angle is observed.
With regard to the permeability of the sand, Van Leussen and Nieuwenhuis found that no large deviations of Darcy's law occur with the water flow through the pores. The found deviations are in general smaller than the accuracy with which the permeability can be determined in situ.
The size of the area where \(\ \partial_\mathrm{e}/\partial_\mathrm{t}\) from equation (6-1) is zero can be clarified by the figures published by van Leussen and Nieuwenhuis. The basis is formed by a cutting process where the density of the sand is increased in a shear band with a certain width. The undisturbed sand has the initial density while the sand after passage of the shear band possesses a critical density. This critical density appeared to be in good accordance with the wet critical density of the used types of sand. This implies that outside the shear band the following equation (Biot (1941)) is valid:
\[\ \left|\frac{\partial^{2} \mathrm{p}}{\partial \mathrm{x}^{2}}\right|+\left|\frac{\partial^{2} \mathrm{p}}{\partial \mathrm{y}^{2}}\right|=\mathrm{0}\tag{6-7}\]
Values for the various densities are given for three types of sand. Differentiation of the residual density as a function of the blade angle is not given. A verification of the water pressures calculations is given for a 60o blade with a blade-height/layer-thickness ratio of 1.
Miedema (1984A) and (1984B) gives a formulation for the determination of the water sub-pressures. The deformation rate is determined by taking the volume balance over the shear zone, as van Os (1977A), (1976) and (1977B) did. The deformation rate is modeled as a boundary condition in the shear zone , while the shear zone is modeled as a straight line instead of a shear band as with van Os (1976), (1977A), (1977B), van Leussen and Nieuwenhuis (1984) and Hansen (1958). The influence of the water depth on the cutting forces is clarified. Steeghs (1985A) and (1985B) developed a theory for the determination of the volume strain rate, based upon a cyclic deformation of the sand in a shear band. This implies that not an average value is taken for the volume strain rate but a cyclic, with time varying, value, based upon the dilatancy angle theory.
Miedema (1985A) and (1985B) derives equations for the determination of the water sub-pressures and the cutting forces, based upon Miedema (1982), (1984A) and (1984B). The water sub-pressures are determined with a finite element method. Explained are the influences of the permeability of the disturbed and undisturbed sand and the determination of the shear angle. The derived theory is verified with model tests. On basis of this research nmax is chosen for the residual pore percentage instead of the wet critical density.
Steeghs (1985A) and (1985B) derives equations for the determination of the water sub-pressures according to an analytical approximation method. With this approximation method the water sub-pressures are determined with a modification of equation (6-4) derived by van Os (1976), (1977A), (1977B) and the storage equation (6-7). Explained is how cutting forces can be determined with the force equilibrium on the cut layer. Also included are the gravity force, the inertia forces and the sub-pressure behind the blade. For the last influence factor no formulation is given. Discussed is the determination of the shear angle. Some examples of the cutting forces are given as a function of the cutting velocity, the water depth and the sub-pressure behind the blade. A verification of this theory is not given.
Miedema (1986A) develops a calculation model for the determination of the cutting forces on a cutter-wheel based upon (1985A) and (1985B). This will be discussed in the appropriate section. Also nomograms are published with which the cutting forces and the shear angle can be determined in a simple way. Explained is the determination of the weighted average permeability from the permeability of the disturbed and undisturbed sand. Based upon the calculations it is concluded that the average permeability forms a good estimation.

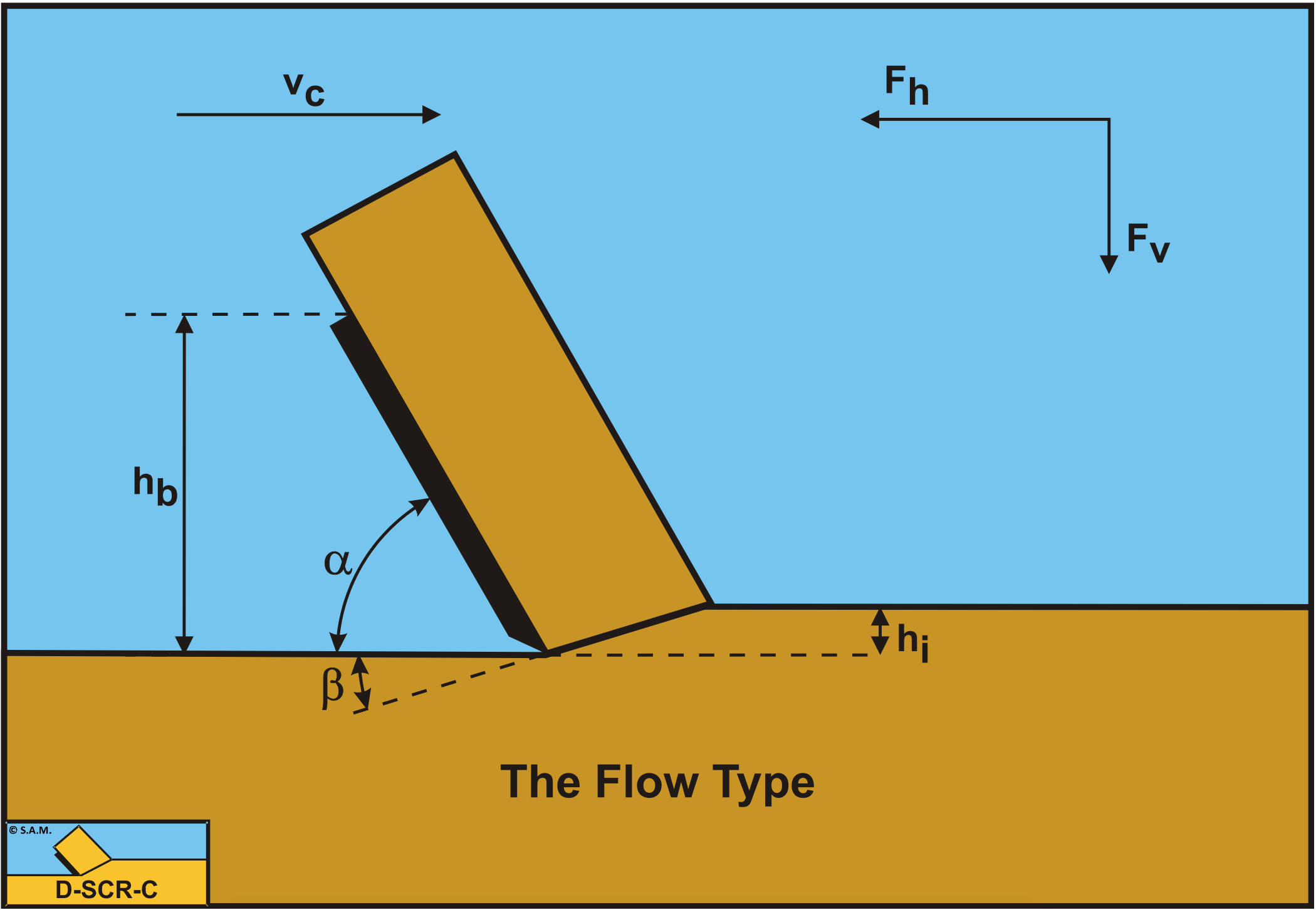
Miedema (1986B) extends the theory with adhesion, cohesion, inertia forces, gravity, and sub-pressure behind the blade. The method for the calculation of the coefficients for the determination of a weighted average permeability are discussed. It is concluded that the additions to the theory lead to a better correlation with the tests results.
Van Os and van Leussen (1987 December) summarize the publications of van Os (1976), (1977A), (1977B) and of Van Leussen and Nieuwenhuis (1984) and give a formulation of the theory developed in the early seventies at the Waterloopkundig Laboratorium. Discussed are the water pressures calculation, cavitation, the weighted average permeability, the angle of internal friction, the soil/steel angle of friction, the permeability, the volume strain and the cutting forces. Verification is given of a water pressures calculation and the cutting forces. The water sub-pressures are determined with equation (6-4) derived by van Os (1976), (1977A) and (1977B). The water pressures calculation is performed with the finite difference method, in which the height of the shear band is equal to the mesh width of the grid. The size of this mesh width is considered to be arbitrary. From an example, however, it can be seen that the shear band has a width of 13% of the layer-thickness. Discussed is the determination of a weighted average permeability. The forces are determined with Coulomb's method.


