6.13: Experiments
- Page ID
- 33968
6.13.1. Description of the Test Facility
The tests with the straight blades are performed on two locations:
-
The old laboratory of Dredging Engineering, which will be called the old laboratory DE.
-
The new laboratory of Dredging Engineering, which will be called the new laboratory DE.
The test stand in the old laboratory DE consists of a concrete tank, 30 m long, 2.5 m wide and 1.35 m high, filled with a layer of 0.5 m sand with a d50 of 200 μm and above the sand 0.6 m water. The test stand in the new laboratory DE consists of a concrete tank, 33 m long, 3 m wide and internally 1.5 m high, with a layer of 0.7 m sand with a d50 of 105 μm and above the sand 0.6 m water. In both laboratories a main carriage can ride over the full length of the tank, pulled by two steel cables. These steel cables are winded on the drums of a hydraulic winch, placed in the basement and driven by a squirrel-cage motor of 35 kW in the old laboratory DE and 45 kW in the new laboratory DE.
In the old laboratory DE the velocity of the carriage could be infinitely variable controlled from 0.05 m/s to 2.50 m/s, with a pulling force of 6 kN. In the new laboratory DE the drive is equipped with a hydraulic two-way valve, which allows for the following speed ranges:
-
A range from 0.05 m/s to 1.40 m/s, with a maximum pulling force of 15 kN.
-
A range from 0.05 m/s to 2.50 m/s, with a maximum pulling force of 7.5 kN.
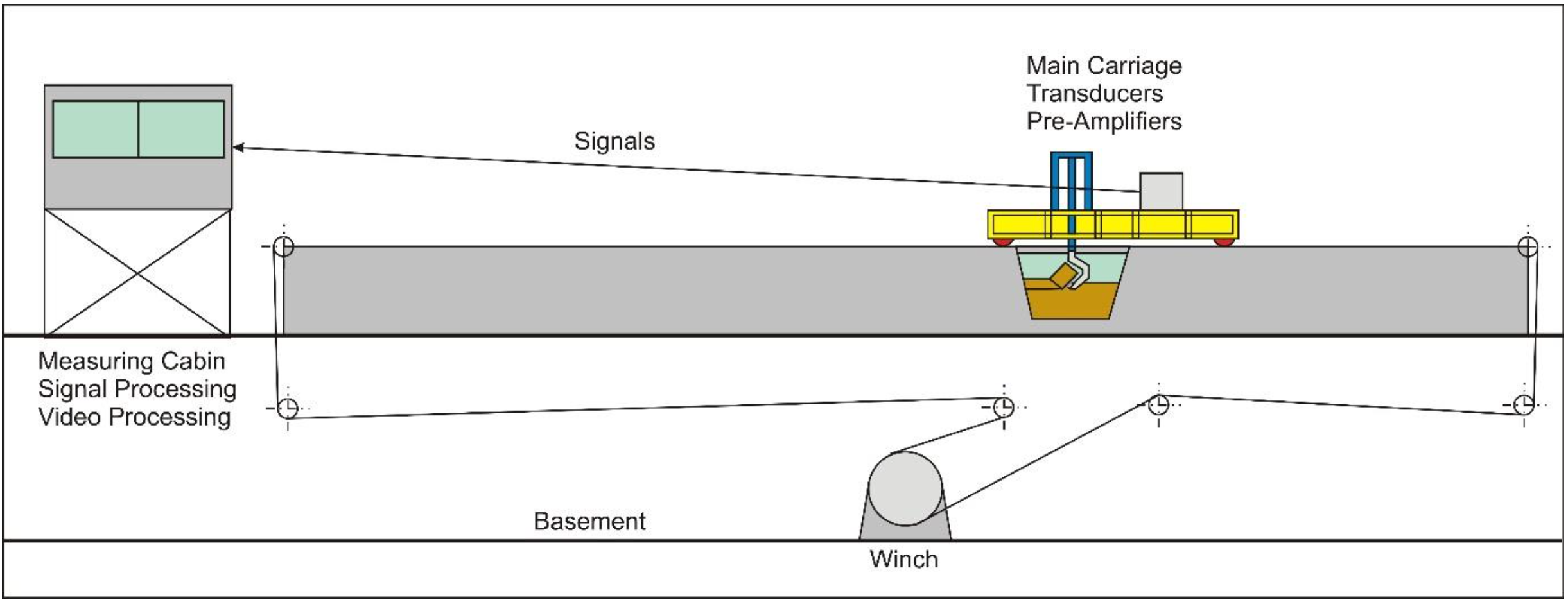
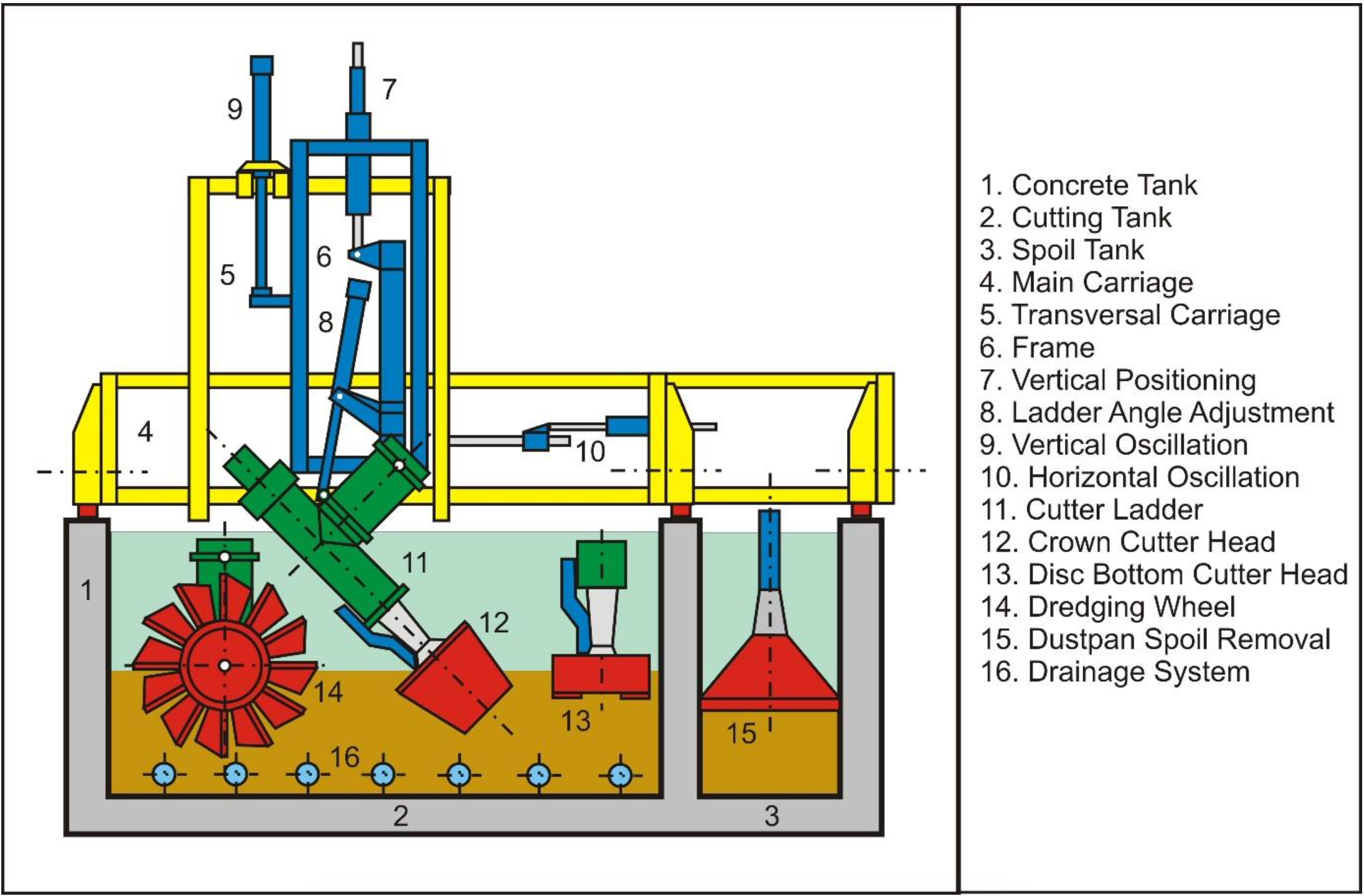
An auxiliary carriage, on which the blades are mounted, can be moved transverse of the longitudinal direction on the main carriage. Hydraulic cylinders are used to adjust the cutting depth and to position the blades in the transverse direction of the tank. Figure 6-36 shows a side view of the concrete tank with the winch drive in the basement and Figure 6-37 shows a cross section with the mounting of cutter heads or the blades underneath the auxiliary carriage (in the new laboratory DE). The main difference between the two laboratories is the side tank, which was added to dump the material excavated. This way the water stays clean and under water video recordings are much brighter. After a test the material excavated is sucked up by a dustpan dredge and put back in the main tank. The old laboratory DE was removed in 1986, when the new laboratory was opened for research. Unfortunately, the new laboratory stopped existing in 2005. Right now there are two such laboratories in the world, one at Texas A&M University in College Station, Texas, USA and one at Hohai University, Changzhou, China. Both laboratories were established around 2005.
Figure 6-38 and Figure 6-39 give an overview of both the old and the new laboratories DE, while Figure 6-40 shows a side view of the carriage, underneath which the blades are mounted.
Removing the spoil tank (3) from this figure gives a good impression of the cutting tank in the old laboratory DE. Instead of a cutter head, blades are mounted under the frame (6) during the cutting tests.

The tests are carried out using a middle blade, flanked on both sides by a side blade, in order to establish a two- dimensional cutting process on the middle blade. The middle blade (center blade) is mounted on a dynamometer, with which the following loads can be measured:
-
The horizontal force
-
The vertical force
-
The transverse force
-
The bending moment
The side blades are mounted in a fork-like construction, attached to some dynamometers, with which the following loads can be measured:
-
The horizontal force
-
The vertical force
Figure 6-41 and Figure 6-42 show the mounting construction of the blades.

In the middle blade, four pore pressure transducers are mounted, with which the pore pressure distribution on the blade can be measured. However no tests are performed in which the forces on the side blades and the pore pressures are measured at the same time. The measuring signals of the dynamometers and the pressure transducers are transmitted to a measurement compartment through pre-amplifiers on the main carriage. In this measurement compartment the measuring signals are suited by 12 bit, 400 Hz A/D converters for processing on a P.C. (personal computer), after which the signals are stored on a flexible disk. Next to the blades, under water, an underwater video camera is mounted to record the cutting process. This also gives a good impression of the shear angles occurring.


Figure 6-44 shows how a blade is mounted under the carriage in the new laboratory DE, in this case for so called snow-plough research. Figure shows the center blade and the two side blades mounted under the carriage in the old laboratory DE. In the center blade the 4 pore pressure transducers can be identified (the white circles) with which the pore pressures are measured.
Figure 6-47 shows the signal processing unit on the carriage, including pre-amplifiers and filters. The pre- amplifiers are used to reduce the noise on the signals that would occur transporting the signals over long distance to the measurement cabin.
Figure 6-46 shows the device used to measure the cone resistance of the sand before every experiment. The cone resistance can be related to the porosity of the sand, where the porosity relates to both the internal and external friction angle and to the permeability.
Figure 6-48 shows the measurement cabin with a PC for data processing and also showing the video screen and the tape recorder to store the video images of all the experiments.
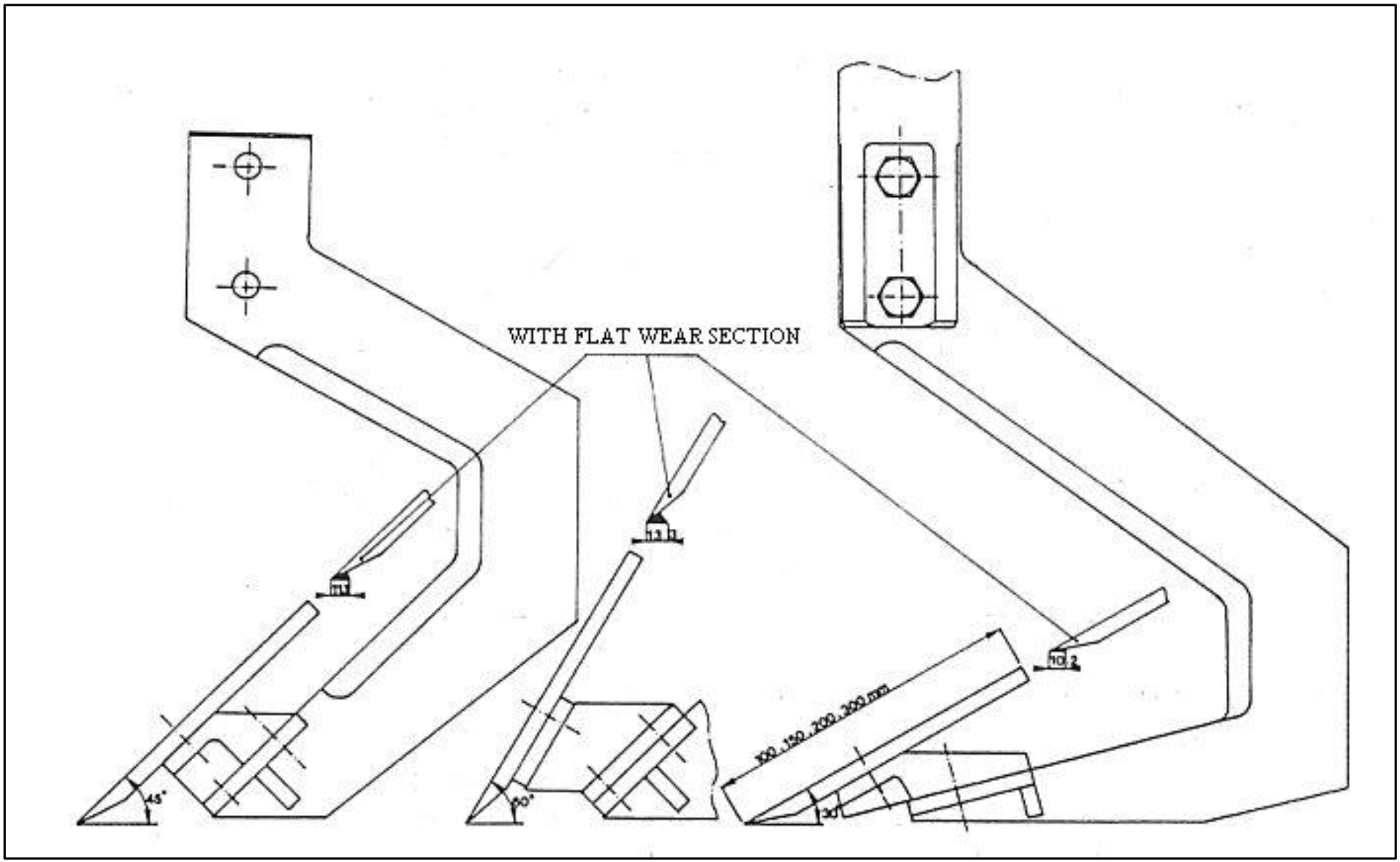
Figure 6-45 shows a side view of the center blades. These blades could also be equipped with a wear flat to measure the influence of worn blades.






6.13.2. Test Program
The theory for the determination of the forces that occur during the cutting of fully water saturated sand with straight blades is verified in two types of sand, sand with a d50 of 200 μm and sand with a d50 of 105 μm. The soil mechanical parameters of these two types of sand can be found in 0 and 0
The research can be subdivided in a number of studies:
-
Research of the water resistance of the blades
-
Research of the accuracy of the assumed two-dimensional character of the cutting process on the middle blade by changing the width of the middle blade with a total width of the middle blade and the side blades of 520 mm. This research is performed in the 200 μm sand.
-
Research of the quantitative character of the side effects in relation to the size and the direction of the cutting forces. This research is performed in the 200 μm sand.
-
Research of the in the theory present scale rules. This research is performed in the 200 μm sand.
-
Research of the accuracy of the theory of the cutting forces and the water sub-pressures in the non-cavitating cutting process. This research is performed in the 200 μm sand.
-
Research of the accuracy of the theory of the forces and the water sub-pressures in the non-cavitating and the partly cavitating cutting process. This research is performed in the 105 μm sand.
From points 4 and 5 it has also been established that the maximum pore percentage of the sand can be chosen for the residual pore percentage. In the 200 μm the dry critical density, the wet critical density and the minimal density are determined, while in the 105 μm sand the wet critical density and the minimal density are determined. These pore values can be found in Appendix K and Appendix L
For both type of sand only the minimal density (maximum pore percentage nmax) gives a large enough increase in volume to explain the measured water sub-pressures. This is in contrast to Van Leussen and Nieuwenhuis (1984) and Van Leussen and Van Os (1987 December), where for the residual density the wet critical density is chosen.
6.13.3. Water Resistance
The water resistance is investigated under circumstances comparable with the cutting tests as far as scale; blade width and cutting velocity are concerned. Since the water resistance during all these tests could be neglected in comparison with the cutting forces, performed under the same conditions (maximum 2%), the water resistance terms are neglected in the further verification. The water resistance could however be more significant at higher cutting velocities above 2 m/s. It should be noted that at higher cutting velocities also the cutting forces will be higher, especially for the non-cavitating cutting process. Further, the inertial force, which is neglected in this research, may also play a role at very high cutting velocities.
6.13.4. The Influence of the Width of the Blade
The blade on which the cutting forces are measured is embedded between two side blades. These side blades have to take care of the three-dimensional side effects, so that on the middle blade a two-dimensional cutting process takes place. The question now is how wide the side blades need to be, at a certain cutting depth, to avoid a significant presence of the side effects on the middle blade. Essential is, that at the deepest cutting depth the side effects on the middle blade are negligible. For this research the following blade configurations are used:
-
A middle blade of 150 mm and two side blades of 185 mm each.
-
A middle blade of 200 mm and two side blades of 160 mm each.
-
A middle blade of 250 mm and two side blades of 135 mm each.
The total blade width in each configuration is therefore 520 mm. The results of this research are, scaled to a middle blade of 200 mm wide, shown in Table 6-2, in which every value is the average of a number of tests. In this table the forces on the 0.20 m and the 0.25 m wide blade are listed in proportion to the 0.15 m wide blade. The change of the direction of the forces in relation to the 0.15 m wide blade is also mentioned. From this table the following conclusions can be drawn:
-
There is no clear tendency to assume that the side effects influence the cutting forces in magnitude.
-
The widening of the middle blade and thus narrowing the side blades, gives slightly more downward aimed forces on the middle blade at a blade angle of 30o. At a blade angle of 45o this tendency can be seen at a blade- height/layer-thickness ratio of 1 and 2, while at a blade-height/ layer-thickness ratio of 3 the forces are just slightly aimed upward. The 60o blade angle gives the same image as the 45o blade angle, however with smaller differences in proportion to the 0.15 m wide blade.
|
w=0.20 m (2) |
w=0.25 m (3) |
||||
|
α |
hb/hi |
ct2/ct1 |
θt2-θt1 |
ct3/ct1 |
θt3-θt1 |
|
30° |
1 |
0.95 |
+1.0° |
1.02 |
+1.0° |
|
30° |
2 |
1.10 |
+2.0° |
0.93 |
+4.0° |
|
30° |
3 |
0.96 |
+5.0° |
1.05 |
+7.0° |
| 45° | 1 | 1.08 | +3.0° | 1.01 | +5.0° |
| 45° | 2 | 0.93 | +3.0° | 0.93 | +5.0° |
| 45° | 3 | 0.93 | -8.0° | 1.07 | -5.0° |
|
60° |
1 |
1.09 |
+0.0° |
1.00 |
+1.0° |
|
60° |
2 |
0.90 |
+1.0° |
0.92 |
+2.0° |
|
60° |
3 |
1.04 |
-5.0° |
0.99 |
-4.0° |
The total measured cutting force ct and the force direction θt, at a blade width of 0.20 m (ct2, θt2) (2) and a blade width of 0.25 m (ct3, θt3) (3) in proportion to the total cutting force and direction at a blade width of 0.15 m (ct1, θt1) (1), according the blade configurations mentioned here.
6.13.5. Side Effects
On the outside of the side blades a three-dimensional cutting process acts, in a sense that the shear zone here is three-dimensional, but on top of that the water flows three-dimensional to the shear zone. This makes the cutting forces differ, in magnitude and direction, from the two-dimensional cutting process. Additionally it is imaginable that also forces will act on the blade in the transversal direction (internal forces in the blade). The influence of the side effects is researched by measuring the forces on both the middle blade as on the side blades. Possible present transversal forces are researched by omitting one side blade in order to be able to research the transversal forces due to the three-dimensional side effects. For this research the following blade configurations are used:
-
A middle blade of 150 mm and two side blades of 185 mm each.
-
A middle blade of 200 mm and two side blades of 160 mm each.
-
A middle blade of 250 mm and two side blades of 135 mm each.
-
A middle blade of 200 mm and one side blade of 160 mm
The results of this research can be found in Table 6-3, where every value represents the average of a number of tests. The cutting forces in this table are scaled to the 200 mm blade to simulate a middle blade without side blades.
|
w=.15 m (1) |
w=.20 m (2) |
w=.25 m (3) |
w=.20 m (4) |
||||||
| α |
hb/hi |
cr |
θr |
cr |
θr |
cr |
θr | cr | θr |
|
30° |
1 |
1.06 |
+26° |
1.23 |
+14° |
1.17 |
+11° |
1.01 |
+13° |
|
30° |
2 |
0.78 |
+18° |
0.87 |
+16° |
0.83 |
+10° |
1.14 |
+10° |
|
30° |
3 |
0.74 |
+22° |
0.56 |
+22° |
0.53 |
+11° |
1.45 |
+ 6° |
|
45° |
1 |
1.13 |
+23° |
1.10 |
+14° |
1.26 |
+ 9° |
1.04 |
+ 5° |
|
45° |
2 |
0.94 |
+19° |
0.94 |
+11° |
0.93 |
+ 7° |
0.92 |
+ 7° |
|
45° |
3 |
0.79 |
+14° |
1.10 |
+17° |
0.98 |
+11° |
0.85 |
+ 6° |
|
60° |
1 |
1.10 |
+ 8° |
1.10 |
+ 6° |
1.10 |
+ 5° |
1.04 |
+ 2° |
|
60° |
2 |
0.94 |
+12° |
1.10 |
+ 8° |
1.06 |
+ 6° |
0.91 |
+ 2° |
|
60° |
3 |
0.77 |
+ 8° |
0.99 |
+15° |
1.02 |
+11° |
0.86 |
+ 3° |
The cutting force on the side blades in ratio to the cutting force on the middle blade cr, assuming that the cutting process on the middle blade is two-dimensional. Also shown is the change of direction of the total cutting force θr. The cutting forces are scaled to the width of the middle blade for the blade widths 0.15 m (1), 0.20 m (2) and 0.25 m (3). The second column for w=.20 m (4) contains the results of the tests with only one side blade to measure the side effects on the middle blade. The measured cutting forces are compared to the similar tests where two side blades are used. The blade configurations are according to chapter 6.13.4. From this research the following conclusions can be drawn:
-
For all blade angles the cutting force on the edge is larger than follows from the two-dimensional process, for a blade-height / layer-thickness ratio of 1.
-
A blade-height / layer-thickness ratio of 2 or 3 shows a somewhat smaller cutting force with a tendency to smaller forces with a higher blade-height / layer-thickness ratio.
-
The direction of the cutting force is, for all four blade configurations, aimed more downwards on the sides than in the middle, where the differences with the middle blade decrease with a wider middle blade and therefore less wide side blades. This implies that, with the widening of the middle blade, the influence of the three-dimensional cutting process on the middle blade increases with a constant total blade width. This could be expected. It also explains that the cutting force in the middle blade is directed more downwards with an increasing middle blade width.
-
Blade configuration 4 differs slightly, as far as the magnitude of the forces is concerned, from the tendency seen in the other three configurations with the 30 blade. The direction of the cutting forces match with the other configurations. It has to be remarked that in this blade configuration the side effects occur only on one side of the blade, which explains the small change of the cutting forces.
-
The measured transverse forces for blade configuration 4 are in the magnitude of 1% of the vector sum of the horizontal and the vertical cutting forces and therefore it can be concluded that the transverse forces are negligible for the used sand.
The conclusions found are in principle only valid for the sand used. The influence of the side effects on the magnitude and the direction of the expected cutting forces will depend on the ratio between the internal friction of the sand and the soil/steel friction. This is because the two-dimensional cutting process is dominated by both angles of friction, while the forces that occur on the sides of the blade, as a result of the three-dimensional shear plane, are dominated more by the internal friction of the sand.
6.13.6. Scale Effects
The soil mechanical research showed that the density of the sand increases slightly with the depth. Since both the permeability and the volume strain, and less significant the other soil mechanical parameters, are influenced by the density, it is important to know the size of this influence on the cutting forces (assuming that the two- dimensional cutting theory is a valid description of the process). If the two-dimensional cutting theory is a valid description of the process, the dimensionless cutting forces will have to give the same results for similar geometric ratios, independent of the dimensions and the layer-thickness, according to the equations for the non-cavitating cutting process and the cavitating cutting process. The following blade configurations are used to research the scaling influence:
-
A blade with a width of 150 mm wide and a height of 100 mm.
-
A blade with a width of 150 mm wide and a height of 150 mm.
-
A blade with a width of 150 mm wide and a height of 200 mm.
-
A blade with a width of 150 mm wide and a height of 300 mm.
The results of this research can be found in Table 6-4, where every value represents the average value of a number of tests.
|
Configuration |
1 |
2 |
3 |
4 |
|
|
α |
hb/hi |
h = 0.10 |
0.15 |
0.20 |
0.30 |
|
30° |
1 |
0.93 |
1.00 |
0.94 |
1.18 |
|
30° |
2 |
1.23 |
1.00 |
1.06 |
1.13 |
|
30° |
3 |
---- |
1.00 |
0.89 |
0.90 |
|
45° |
1 |
0.95 |
1.00 |
1.13 |
---- |
|
45° |
2 |
0.89 |
1.00 |
1.05 |
1.30 |
|
45° |
3 |
---- |
1.00 |
1.02 |
1.13 |
|
60° |
1 |
0.91 |
1.00 |
---- | ---- |
|
60° |
2 |
0.90 |
1.00 |
1.19 |
1.04 |
|
60° |
3 |
1.02 |
1.00 |
1.13 |
1.21 |
The total cutting force ct with blade heights of 0.10 m (1), 0.15 m (2), 0.20 m (3) and 0.30 m (4) in proportion to the cutting force at a blade height 0.15 m (2). The blade configurations are according chapter 6.13.4. Because the influences of the gravity and inertia forces can disturb the character of the dimensionless forces compared to 0 to 0, the measured forces are first corrected for these influences. The forces in the table are in proportion to the forces that occurred with blade configuration 2. The following conclusions can be drawn from the table:
-
There is a slight tendency to larger dimensionless forces with increasing dimensions of the blades and the layer-thickness, which could be expected with the slightly increasing density.
-
For a blade angle of 30o and a blade-height / layer-thickness ratio of 2, large dimensionless forces are measured for blade configuration 1. These are the tests with the thinnest layer-thickness of 25 mm. A probable cause can be that the rounding of the blade tip in proportion with the layer-thickness is relatively large, leading to a relatively large influence of this rounding on the cutting forces. This also explains the development of the dimensionless forces at a blade angle of 30o and a blade-height / layer-thickness ratio of 3.
6.13.7. Comparison of Measurements versus Theory
The results of the preceding three investigations are collected in Table 6-5, compared with the theory. Every value is the average of a number of tests. In the table it can be found:
-
The dimensionless forces, the average from the several scales and blade widths.
-
As 1, but corrected for the gravity and inertia forces.
-
The theoretical dimensionless forces according to Appendix D to Appendix J.
|
measured |
calculated |
||||||
|
not-corrected |
corrected |
theoretical |
|||||
|
α |
hb/hi |
ct |
θt |
ct | θt | ct | θt |
|
30° |
1 |
0.52 |
+13.3° |
0.48 |
+17.1° |
0.39 |
+28.3° |
|
30° |
2 |
0.56 |
+17.0° |
0.53 |
+20.1° |
0.43 |
+27.4° |
|
30° |
3 |
0.56 |
+24.8° |
0.53 |
+28.2° |
0.43 |
+27.3° |
|
45° |
1 |
0.71 |
+ 4.9° |
0.63 |
+ 7.5° |
0.49 |
+12.9° |
|
45° |
2 |
0.75 |
+ 6.0° |
0.66 |
+ 8.0° |
0.57 |
+10.7° |
|
45° |
3 |
0.76 |
+ 5.1° |
0.70 |
+ 6.9° |
0.61 |
+ 9.9° |
|
60° |
1 |
1.06 |
+ 1.2° |
0.88 |
+ 1.9° |
0.69 |
- 0.7° |
|
60° |
2 |
1.00 |
- 2.4° |
0.84 |
- 3.4° |
0.83 |
- 3.2° |
|
60° |
3 |
0.99 |
- 3.4° |
0.85 |
- 4.2° |
0.91 |
- 4.6° |
The total cutting force measured (not-corrected and corrected for the gravity and inertia forces) and the theoretical total cutting forces (all dimensionless). The theoretical values for ct and θt are based on an angle of internal friction of 38o, a soil/steel angle of friction of 30o and a weighted average permeability of approximately 0.000242 m/s dependent on the weigh factor a1. The total cutting force ct and the force direction θt are determined according chapter 6.12.4. The following conclusions can be drawn from this table:
-
The measured and corrected cutting forces are larger than the, according to the theory, calculated cutting forces, at blade angles of 30o and 45o. The differences become smaller with an increase in the blade angle and when the blade-height / layer-thickness ratio increases.
-
For a blade angle of 60o the corrected measure forces agree well with the calculated forces.
-
The tendency towards larger forces with a larger blade-height / layer-thickness ratio (theory) is clearly present with blade angles 30o and 45o.
-
At a blade angle of 60o the forces seem to be less dependent of the blade-height / layer-thickness ratio.
-
The direction of the measured cutting forces agrees well with the theoretical determined direction. Only at the blade angle of 30o the forces are slightly aimed more upward for the blade-height / layer-thickness ratios 1 and 2.
-
Neglecting the inertia forces, gravity, etc. introduces an error of at least 15% within the used velocity range. This error occurs with the 60o blade, where the cutting velocity is the lowest of all cutting tests and is mainly due to the gravity.
Considering that the sand, in the course of the execution of the tests, as a result of segregation, has obtained a slightly coarser grain distribution and that the tests are performed with an increasing blade angle, can be concluded that the test results show a good correlation with the theory. It has to be remarked, however, that the scale and side effects can slightly disturb the good correlation between the theory and the measurements.
6.13.8. Location of the Resulting Cutting Force
A quantity that is measured but has not been integrated in the theory is the location of the resulting cutting force. This quantity can be of importance for the determination of the equilibrium of a drag head. The locations, of the in this chapter performed tests, are listed in Table 6-6. Table 6-7 lists the dimensionless locations of the resulting cutting force, in relation with the layer-thickness.
|
Configuration |
1 |
2 |
3 |
4 |
|
|
α |
hb/hi |
h = 0.10 |
0.15 |
0.20 |
0.30 |
|
30° |
1 |
51.25 |
63.1 |
96.7 |
157.2 |
|
30° |
2 |
76.00 |
55.7 |
61.3 |
84.8 |
|
30° |
3 |
---- |
50.5 |
54.3 |
71.5 |
|
45° |
1 |
66.38 |
87.5 |
128.0 |
---- |
|
45° |
2 |
55.13 |
56.9 |
73.4 |
128.6 |
|
45° |
3 |
---- |
62.0 |
56.0 |
82.1 |
|
60° |
1 |
69.88 |
99.5 |
---- |
---- |
|
60° |
2 |
50.00 |
68.4 |
86.1 |
123.9 |
|
60° |
3 |
46.25 |
55.0 |
66.3 |
95.1 |
The location of the resulting cutting force in mm from the blade tip, for the blade configurations of chapter 6.13.4.
|
Configuration |
|
1 |
2 |
3 |
4 |
| α |
hb/hi |
h = 0.10 |
0.15 |
0.20 |
0.30 |
|
30° |
1 |
0.51 |
0.42 |
0.48 |
0.59 |
|
30° |
2 |
1.52 |
0.75 |
0.61 |
0.56 |
|
30° |
3 |
---- |
1.01 |
0.82 |
0.71 |
|
45° |
1 |
0.67 |
0.58 |
0.64 |
---- |
|
45° |
2 |
1.11 |
0.76 |
0.63 |
0.73 |
|
45° |
3 |
---- |
1.25 |
0.84 |
0.83 |
|
60° |
1 |
0.70 |
0.66 |
---- |
---- |
|
60° |
2 |
1.01 |
0.91 |
0.86 |
0.83 |
|
60° |
3 |
1.38 |
1.11 |
0.99 |
0.95 |
The location of the resulting cutting force from the blade tip, along the blade, made dimensionless by dividing with the layer-thickness, for the blade configurations of chapter 6.13.4. From these tables the following conclusions can be drawn:
-
The location of the resulting cutting force is closer to the blade tip with larger blade dimensions.
-
The location of the resulting cutting force is closer to the blade tip with a smaller blade-height / layer-thickness ratio.
The first conclusion can be based upon the fact that a possible present adhesion, on a larger scale (and therefore layer-thickness) causes, in proportion, a smaller part of the cutting force. For the second conclusion this can also be a cause, although the blade-height / layer-thickness ratio must be seen as the main cause.
6.13.9. Verification of the Theory in 200 μm Sand
The linear cutting theory is researched on three points:
-
The distribution of the water sub-pressures on the blade for a blade with a radius of rounding of 1 mm.
-
The distribution of the water sub-pressures on the blade for a blade with a flat wear face of approximately 10 mm and a clearance angle of 1o.
-
The correlation between the measured cutting forces and the theoretical cutting forces.
The dimensions of the blades and the wear faces can be found in Figure 6-45. In Table 6-10 the ratios of the wear face length and the layer-thickness are listed. In the preceding paragraph already a few conclusions are drawn upon the correlation between the measured and the calculated cutting forces. In this research both the forces and the water pressures are measured to increase the knowledge of the accuracy of the theory. Also it has to be mentioned that the soil mechanical parameters are determined during this research.
In Figure 6-56 the results of a test are shown. The results of the whole research of the forces are listed in Table 6-8 for the blade with the radius of rounding of 1 mm and in Table 6-9 for the blade with the wear flat. The dimensionless measured water sub-pressures are shown in Appendix M: Experiments in Water Saturated Sand, in which the theoretical distribution is represented by the solid line. The water sub-pressures are made dimensionless, although the weighted average permeability km is used instead of the permeability kmax used in the equations. From this research the following conclusions can be drawn:
-
The measured forces and water sub-pressures show, in general, a good correlation with the theory.
-
The tendency towards increasing and more upward aimed forces with increasing blade angles can be observed clearly in the Table 6-8 and Table 6-9.
-
The ratio between the measured and calculated forces becomes smaller when the blade angle and the blade-height / layer-thickness ratio increase.
-
The cutting forces on the blade with the wear face are almost equal to the cutting forces on the blade with the radius of rounding, but are slightly aimed more upward.
-
The ratio between the measured and calculated water sub-pressures is, in general, smaller than the ratio between the measured and calculated cutting forces.
-
The measured water sub-pressures on the blade with the wear face and the blade with the radius of rounding differ slightly (Table 6-10) from the water sub-pressures on the blade with the radius of rounding. On the 30o and the 45o blade, the water sub-pressures tends to smaller values for the blade with the wear face, although the differences are very small. On the 60o blade these water sub-pressures are slightly higher. Therefore it can be concluded that, for water pressures calculations, the wear-section-length / layer-thickness ratio w/hi has to be chosen dependent of the blade angle. Which was already clear during the tests because the clearance angle increased with a larger blade angle. For the determination of Appendix H to Appendix J, however, the ratio used was w/hi=0.2, which is a good average value.
|
measured |
calculated |
||||||
|
not-corrected |
corrected |
theoretical |
|||||
|
α |
hb/hi |
ct |
θt |
ct |
θt | ct | θt |
|
30° |
1 |
0.54 |
+29.3° |
0.49 |
+29.0° |
0.39 |
+28.3° |
|
30° |
2 |
0.48 |
+27.5° |
0.46 |
+27.2° |
0.43 |
+27.4° |
|
30° |
3 |
0.49 |
+27.6° |
0.46 |
+27.3° |
0.43 |
+27.3° |
|
45° |
1 |
0.78 |
+15.1° |
0.58 |
+13.9° |
0.49 |
+12.9° |
|
45° |
2 |
0.64 |
+12.3° |
0.59 |
+11.6° |
0.57 |
+10.7° |
|
45° |
3 |
0.60 |
+11.0° |
0.55 |
+10.5° |
0.61 |
+ 9.9° |
|
60° |
1 |
1.16 |
+ 0.7° |
0.77 |
- 0.6° |
0.69 |
+ 0.7° |
|
60° |
2 |
0.95 |
- 1.4° |
0.79 |
- 2.2° |
0.83 |
- 3.2° |
|
60° |
3 |
0.93 |
- 3.4° |
0.82 |
- 4.0° |
0.91 |
- 4.6° |
|
60° |
6 |
0.70 |
- 4.8° |
0.64 |
- 5.7° |
1.14 |
- 7.4° |
Measured dimensionless forces, not-corrected and corrected for gravity and inertia forces and theoretical values according to Appendix H to Appendix J for the blade with the radius of rounding and the sub-pressure behind the blade. The theoretical values for ct and θt are determined based on values for the angle of internal friction of 38o, a soil/steel angle of friction of 30o and a weighted average permeability of 0.000242 m/s, dependent on the weigh factor a1.
|
measured |
calculated |
||||||
|
not-corrected |
corrected |
theoretical |
|||||
| α |
hb/hi |
ct |
θt | ct | θt | ct | θt |
|
30° |
1 |
0.53 |
+26.2° |
0.48 |
+25.9° |
0.39 |
+28.3° |
|
30° |
2 |
0.48 |
+24.0° |
0.46 |
+23.7° |
0.43 |
+27.4° |
|
30° |
3 |
0.49 |
+24.7° |
0.46 |
+24.3° |
0.43 |
+27.3° |
|
45° |
1 |
0.72 |
+11.9° |
0.57 |
+11.0° |
0.49 |
+12.9° |
|
45° |
2 |
0.66 |
+ 8.8° |
0.60 |
+ 8.3° |
0.57 |
+10.7° |
|
45° |
3 |
0.63 |
+ 7.8° |
0.60 |
+ 7.3° |
0.61 |
+ 9.9° |
|
60° |
1 |
----- |
----- | ----- | ----- | ----- | ----- |
|
60° |
2 |
0.90 |
- 5.6° |
0.80 |
- 6.2° |
0.83 |
- 3.2° |
|
60° |
3 |
0.95 |
- 7.3° |
0.87 |
- 8.0° |
0.91 |
- 4.6° |
|
60° |
6 |
0.70 |
- 9.2° |
0.64 |
-10.1° |
1.14 |
- 7.4° |
Measured dimensionless forces, not-corrected and corrected for gravity and inertia forces and theoretical values according to Appendix H to Appendix J for the blade with the flat wear face and the sub-pressure behind the blade. The theoretical values for ct and θt are determined according chapter 6.12.4. They are based on values for the angle of internal friction of 38o, a soil/steel angle of friction of 30o and a weighted average permeability of 0.000242 m/s, dependent on the weigh factor a1.
| α |
hb/hi |
w |
hi |
w/hi |
p2ma |
p2ms |
p2m |
p2ms/ p2ma |
|
30° |
1 |
10.2 |
100 |
0.102 |
0.076 |
0.073 |
0.076 |
0.96 |
|
30° |
2 |
10.2 |
50 |
0.204 |
0.051 |
0.050 |
0.049 |
0.98 |
|
30° |
3 |
10.2 |
33 |
0.308 |
0.034 |
0.030 |
0.034 |
0.88 |
|
45° |
1 |
11.1 |
141 |
0.079 |
0.090 |
0.080 |
0.097 |
0.89 |
|
45° |
2 |
11.1 |
70 |
0.159 |
0.069 |
0.068 |
0.082 |
0.99 |
|
45° |
3 |
11.1 |
47 |
0.236 |
0.052 |
0.051 |
0.065 |
0.98 |
|
60° |
1 |
13.3 |
173 |
0.077 |
0.107 |
---- |
0.091 |
---- |
|
60° |
2 |
13.3 |
87 |
0.153 |
0.083 |
0.090 |
0.100 |
1.08 |
|
60° |
3 |
13.3 |
58 |
0.229 |
0.075 |
0.081 |
0.094 |
1.08 |
|
60° |
6 |
13.3 |
30 |
0.443 |
0.035 |
0.038 |
0.061 |
1.09 |
The average dimensionless pore pressures on the blade, on the blade with the radius of rounding p2ma and the blade with the wear face p2ms , the theoretical values p2m and the ratio between the sub-pressures p2ms and p2ma, as a function of the length of the wear face w (mm), the layer-thickness hi (mm) and the wear-section-length / layer- thickness ratio.
6.13.10. Verification of the Theory in 105 μm Sand
The linear cutting theory for the 105 μm is investigated on three points:
-
The distribution of the water sub-pressures on the blade in a non-cavitating cutting process.
-
The distribution of the water sub-pressures on the blade in the transition region between the non-cavitating and the cavitating cutting process.
-
The correlation between the measured cutting forces and the theoretical calculated cutting forces.
The dimensions of the blades can be found in Figure 6-45. In this research only a 30o blade with a layer-thickness of 100 mm, a 45o blade with a layer-thickness of 70 mm and a 60o with a layer-thickness of 58 mm, are used, at a blade height h of 200 mm. The soil mechanical parameters of the used sand are listed in Appendix L. The results of the research regarding the cutting forces can be found in Table 6-11.
|
measured |
calculated |
||||||
| α | hb/hi |
ct |
θt | ct | θt | ct | θt |
|
no cavitation |
not-corrected |
corrected |
theoretical |
||||
|
30° |
1 |
.45 |
+16.5° |
.45 |
+25.6° |
.41 |
+25.1° |
|
45° |
2 |
.50 |
- 3.5° |
.47 |
+ 7.2° |
.62 |
+ 7.6° |
|
60° |
3 |
.60 |
- 8.8° |
.58 |
- 6.3° |
1.02 |
- 7.5° |
|
cavitation |
not-corrected |
corrected |
theoretical |
||||
|
30° |
1 |
3.4 |
+13.1° |
3.4 |
+24.2° |
3.3 |
+21.6° |
|
45° |
2 |
4.7 |
-10.3° |
4.2 |
+ 5.7° |
4.6 |
+ 2.6° |
|
60° |
3 |
4.9 |
- 9.0° |
4.8 |
- 7.8° |
6.8 |
-12.1° |
Measured dimensionless forces, not-corrected and corrected for gravity and inertia forces and the theoretical values according to Appendix C to Appendix G for the non-cavitating cutting process and according to Appendix H to Appendix J for the cavitating cutting process, calculated with a sub-pressure behind the blade. The values of ct and θt are calculated according chapter 6.12.4. They are based on values for the angle of internal friction of 38o, a soil/steel angle of friction of 30o and a weighted average permeability between 0.00011 m/s and 0.00012 m/s, dependent on the weigh factor a1 and the initial pore percentage of the sand bed.
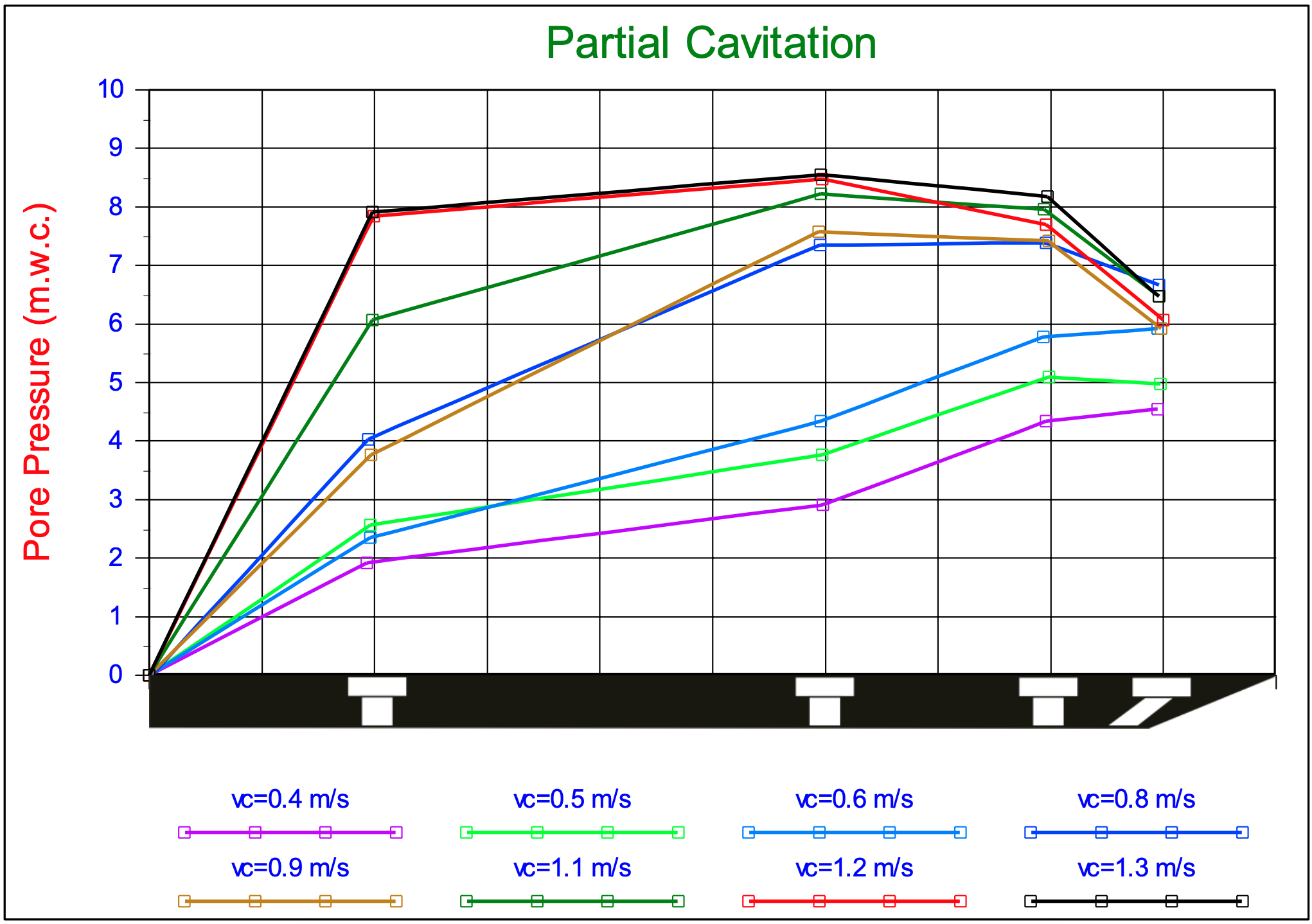
The dimensionless measured water sub-pressures of the non-cavitating cutting process are presented in Appendix M, in which the solid line represents the theoretical distribution. The dimensionless measured water sub-pressures in the transition region are also presented in Appendix M. The figures in Appendix M show the measured horizontal forces Fh, in which the solid line represents the theoretical distribution. Other figures show the measured vertical forces Fv, in which the solid line represents the theoretical distribution. Also shown in is the distribution of the forces, for several water depths, during a fully cavitating cutting process (the almost horizontal lines). From this research the following conclusions can be drawn:
-
The tests with the 30o blade give a good correlation with the theory, both for the forces as for the water sub- pressures. For the 45o blade both the forces and the water sub-pressures are lower than the theoretical calculated values with even larger deviations for the 60o blade. For the 60o blade the forces and the water sub-pressures values are approximately 60% of the calculated values.
-
The direction of the cutting forces agrees reasonably well with the theory for all blade angles, after correction for the gravity and the inertia forces.
-
The figures in Appendix M show that the profile of the water sub-pressures on the blade, clearly changes shape when the peak stress close to the blade tip (sub-pressure) has a value of approximately 65% of the absolute pressure. An increase of the cutting velocity results in a more flattening profile, with a translation of the peak to the middle of the blade. No cavitation is observed but rather an asymptotic approach of the cavitation pressure with an increasing cutting velocity. For the 60o blade the flattening only appears near the blade tip. This can be explained with the large blade-height / layer-thickness ratio. This also explains the low cutting forces in the range where cavitation is expected. There is some cavitation but only locally in the shear zone; the process is not yet fully cavitated.
-
Since, according to the theory, the highest sub-pressures will appear in the shear zone, cavitation will appear there first. The theoretical ratio between the highest sub-pressure in the shear zone and the highest sub-pressure on the blade is approximately 1.6, which is in accordance with conclusion 3. Obviously there is cavitation in the shear zone in these tests, during which the cavitation spot expands to above the blade and higher above the blade with higher cutting velocities.
In Appendix M the pore pressure graphs show this relation between the cavitation spot and the water pressures profile on the blade. The water sub-pressures will become smaller where the cavitation spot ends. This also implies that the measurements give an impression of the size of the cavitation spot.
As soon as cavitation occurs locally in the sand package, it becomes difficult to determine the dimensionless coefficients c1 and c2 or d1 and d2. This is difficult because the cutting process in the transition region varies between a cavitating and a non-cavitating cutting process. The ratio between the average water pressure in the shear zone and the average water pressure on the blade surface changes continuously with an increasing cutting velocity. On top of that the shape and the size of the area where cavitation occurs are unknown. However, to get an impression of the cutting process in the transition region, a number of simplifications regarding the water flow through the pores are carried out.
-
The flow from the free sand surface to the shear zone takes place along circular flow lines (see equations (6-37) and (6-38)), both through the packed sand as through the cut sand. With this assumption the distance from the free sand surface to the cavitation area can be determined, according:
\[\ \xi_{0}=\frac{(\mathbf{z}+\mathbf{1 0})}{\mathbf{v}_{\mathbf{c}} \cdot \mathbf{\varepsilon} \cdot \sin (\beta)} \cdot\left(\frac{\mathbf{k}_{\max }}{\alpha+\beta}+\frac{\mathbf{k}_{\mathbf{i}}}{\pi-\beta}\right) \cdot \sin (\alpha+\beta)\tag{6-107}\]
-
The flow in the cut sand is perpendicular to the free sand surface, from the breakpoint where the shear plane reaches the free sand surface. This flow fills the water vapor bubbles with water. The distance from the free sand surface to the cavitating area can now be determined, under the assumption that the volume flow rate of the vapor bubbles equals the volume flow rate of the dilatancy, according:
\[\ \frac{\mathbf{k}_{\max } \cdot(\mathbf{z}+\mathbf{1 0})}{\xi} \cdot \mathbf{d} \Psi=\mathbf{v}_{\mathbf{c}} \cdot \varepsilon \cdot \frac{\sin (\beta)}{\sin (\alpha+\beta)} \cdot \mathbf{d} \xi\tag{6-108}\]
-
In which the right term represents the volume flow rate of the vapor bubbles from the dilatancy zone, while the left term represents the supply of water from the free sand surface. This is shown in Appendix M the pore pressure graphs. With the initial value from equation (6-107) the following solution can be found:
\[\ \xi=\sqrt{\xi_{0}^{2}+2 \cdot \frac{\mathbf{k}_{\max } \cdot(\mathbf{z}+\mathbf{1 0})}{\left(\mathbf{v}_{\mathbf{c}} \cdot \frac{\sin (\beta)}{\sin (\alpha+\beta)} \cdot \varepsilon\right)} \cdot \Psi}\tag{6-109}\]
The distance from the blade to the cavitation spot is considered to be constant over the blade. The magnitude of this distance is however unknown.
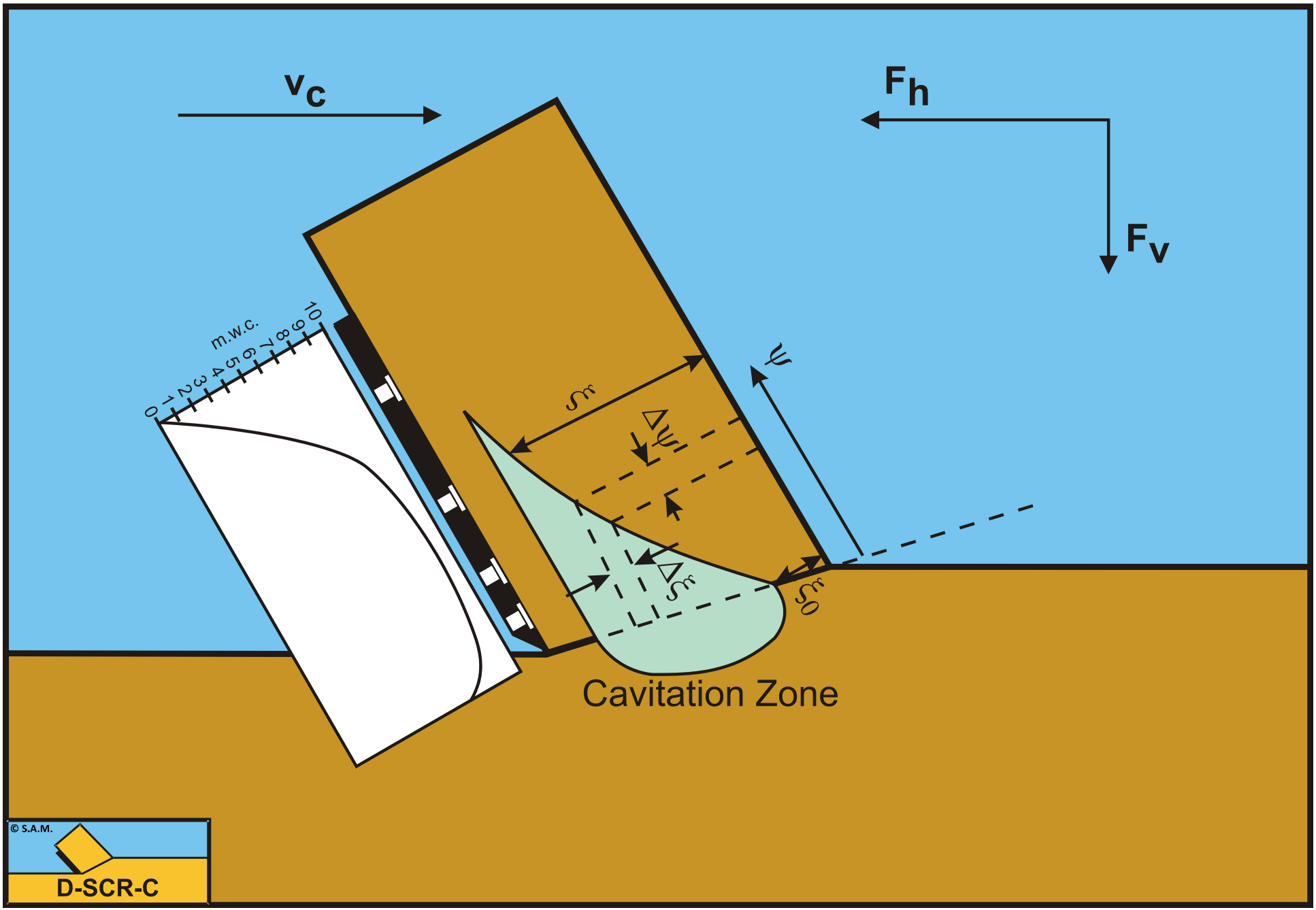
The relation between the dimensions of the cavitation spot, and the water pressure profile on the blade.
The progressive character of the cavitation spot development results from equation (6-109). If, at a certain cutting velocity, cavitation occurs locally in the cavitation zone, then the resulting cavitation spot will always expand immediately over a certain distance above the blade as a result of the fact that a certain time is needed to fill the volume flow rate of the vapor bubbles. The development of the water sub-pressures will, in general, be influenced by the ever in the pore water present dissolved air. As soon as water sub-pressures are developing as a result of the increase in volume in the shear zone, part of the dissolved air will form air bubbles. Since these air bubbles are compressible, a large part of the volume strain will be taken in by the expansion of the air bubbles, which results in a less fast increase of the water sub-pressures with an increasing cutting velocity. The maxima of the water sub- pressures will also be influenced by the present air bubbles. This can be illustrated with the following example: Assume the sand contains 3 volume percent air, which takes up the full volume strain in the dilatancy zone. With a volume strain of 16%, this implies that after expansion, the volume percentage air is 19%. Since it is a quick process, it may be assumed that the expansion is adiabatic, which amounts to maximum water sub-pressures of 0.925 times the present hydrostatic pressure. In an isothermal process the maximum water sub-pressures are 0.842 times the present hydrostatic pressure. From this simple example it can be concluded that the, in the pore water present (either dissolved or not) air, has to be taken into account. In the verification of the water sub-pressures, measured during the cutting tests in the 105 μm sand, the possibility of a presence of dissolved air is recognized but it appeared to be impossible to quantify this influence. It is however possible that the maximum water sub- pressures reached (Appendix M the pore pressure graphs) are limited by the in the pore water present dissolved air.
6.13.11. Determination of φ and δ from Measurements
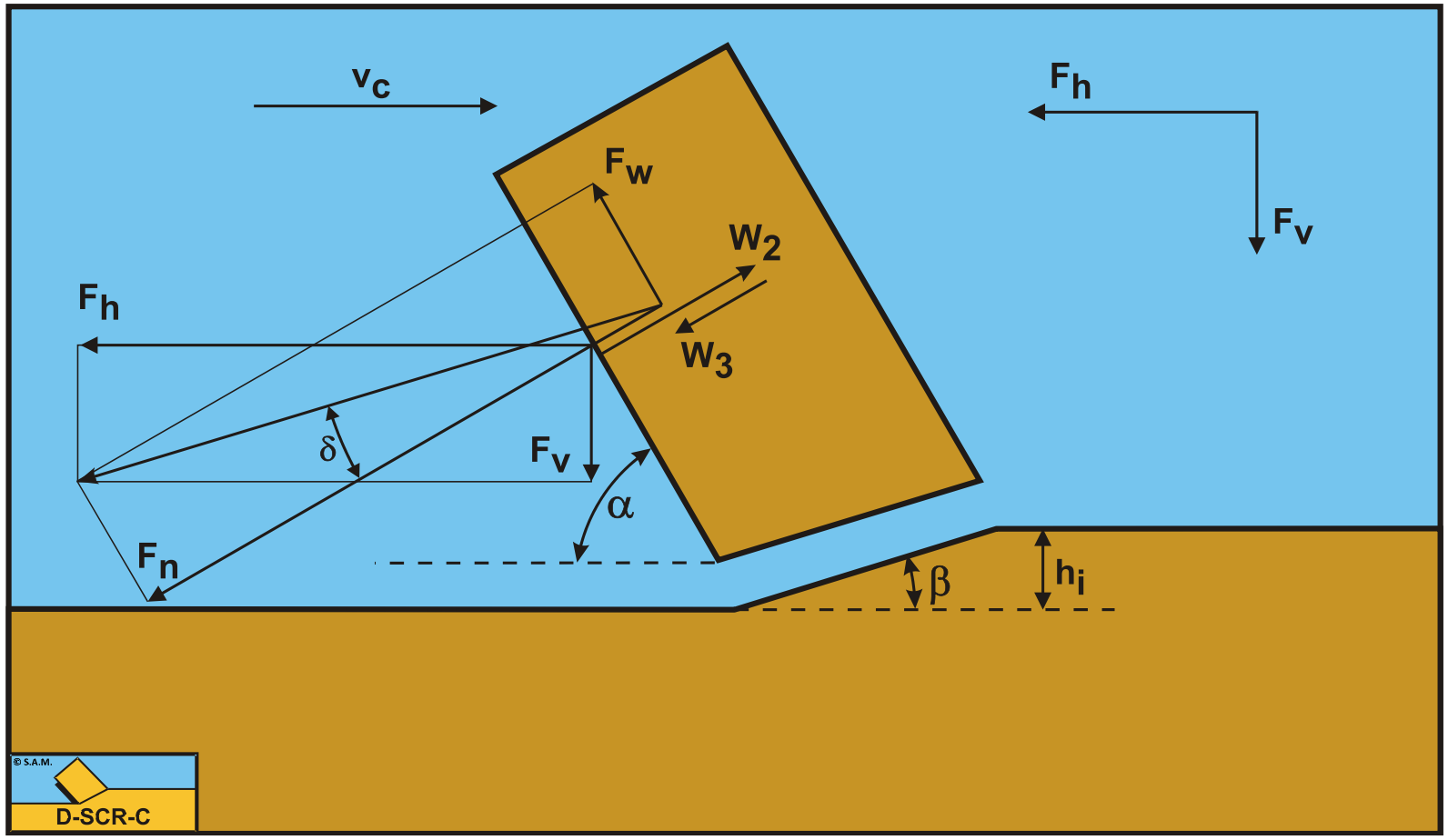
The soil/steel friction angle δ and the angle of internal friction φ can be determined from cutting tests. Sand without cohesion or adhesion is assumed in the next derivations, while the mass of the cut layer has no influence on the determination of the soil/steel friction angle. In Figure 6-51 it is indicated which forces, acting on the blade, have to be measured to determine the soil/steel friction angle δ.
The forces Fh and Fv can be measured directly. Force W2 results from the integration of the measured water pressures on the blade. From this figure the normal force on the blade, resulting from the grain stresses on the blade, becomes:
\[\ \mathrm{F}_{\mathrm{n}}=\mathrm{W}_{\mathrm{2}}-\mathrm{W}_{\mathrm{3}}+\mathrm{F}_{\mathrm{h}} \cdot \sin (\alpha)+\mathrm{F}_{\mathrm{v}} \cdot \cos (\alpha)\tag{6-110}\]
The friction force, resulting from the grain stresses on the blade, becomes:
\[\ \mathrm{F}_{\mathrm{w}}=\mathrm{F}_{\mathrm{h}} \cdot \cos (\alpha)-\mathrm{F}_{\mathrm{v}} \cdot \sin (\alpha)\tag{6-111}\]
The soil/steel angle of friction now becomes:
\[\ \delta=\arctan \left(\frac{\mathrm{F}_{\mathrm{w}}}{\mathrm{F}_{\mathrm{n}}}\right)\tag{6-112}\]
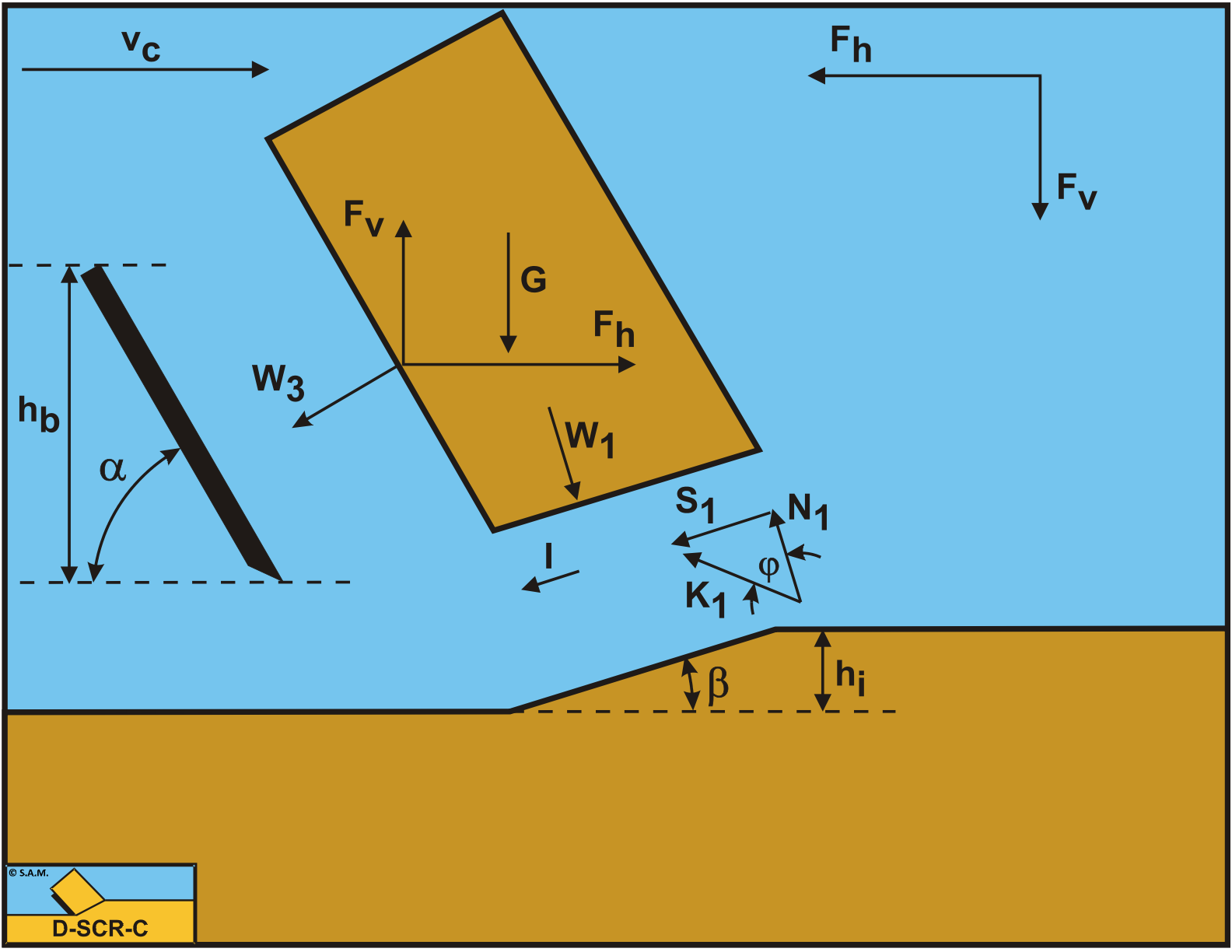
Determination of the angle of internal friction from the cutting tests is slightly more complicated. In Figure 6-52 it is indicated which forces, acting on the cut layer, have to be measured to determine this angle. Directly known are the measured forces Fh and Fv. The force W1 is unknown and impossible to measure. However from the numerical water pressures calculations the ratio between W1 and W2 is known. By multiplying the measured force W2 with this ratio an estimation of the value of the force W1 can be obtained, so:
\[\ \mathrm{W}_{1}=\left(\frac{\mathrm{W}_{1}}{\mathrm{W}_{2}}\right)_{\mathrm{c a l c}} \cdot \mathrm{W}_{2 \mathrm{mean}}\tag{6-113}\]
For the horizontal and the vertical force equilibrium of the cut layer can now be written:
\[\ \mathrm{F}_{\mathrm{h}}-\mathrm{W}_{\mathrm{3}} \cdot \sin (\alpha)=\mathrm{K}_{1} \cdot \sin (\beta+\phi)-\mathrm{W}_{1} \cdot \sin (\beta)+\mathrm{I} \cdot \cos (\beta)\tag{6-114}\]
\[\ \mathrm{F}_{\mathrm{v}}-\mathrm{W}_{\mathrm{3}} \cdot \cos (\boldsymbol{\alpha})=-\mathrm{K}_{\mathrm{1}} \cdot \cos (\boldsymbol{\beta}+\phi)+\mathrm{W}_{\mathrm{1}} \cdot \cos (\boldsymbol{\beta})+\mathrm{I} \cdot \sin (\boldsymbol{\beta})+\mathrm{G}\tag{6-115}\]
The angle of internal friction:
\[\ \mathrm{\phi=\arctan \left(\frac{F_{h}-W_{3} \cdot \sin (\alpha)+W_{1} \cdot \sin (\beta)-I \cdot \cos (\beta)}{-F_{v}+W_{3} \cdot \cos (\alpha)+W_{1} \cdot \cos (\beta)+I \cdot \sin (\beta)+G}\right)-\beta}\tag{6-116}\]
The equations derived (6-112) and (6-116) are used to determine the values of φ and δ from the cutting tests carried out. The soil/steel friction angle can quite easily be determined, with the remark that the side and wear effects can influence the results from this equation slightly. The soil/steel friction angle, determined with this method, is therefore a gross value. This value, however, is of great practical importance, because the side and wear effects that occur in practice are included in this value.
The soil/steel friction angle δ, determined with this method, varied between 24o and 35o, with an average of approximately 30o. For both types of sand almost the same results were found for the soil/steel friction angle. A clear tendency towards stress or blade angle dependency of the soil/steel angle of friction is not observed. This in contrast to Van Leussen and Nieuwenhuis (1984), who found a blade angle dependency according Hettiaratchi and Reece (1974).
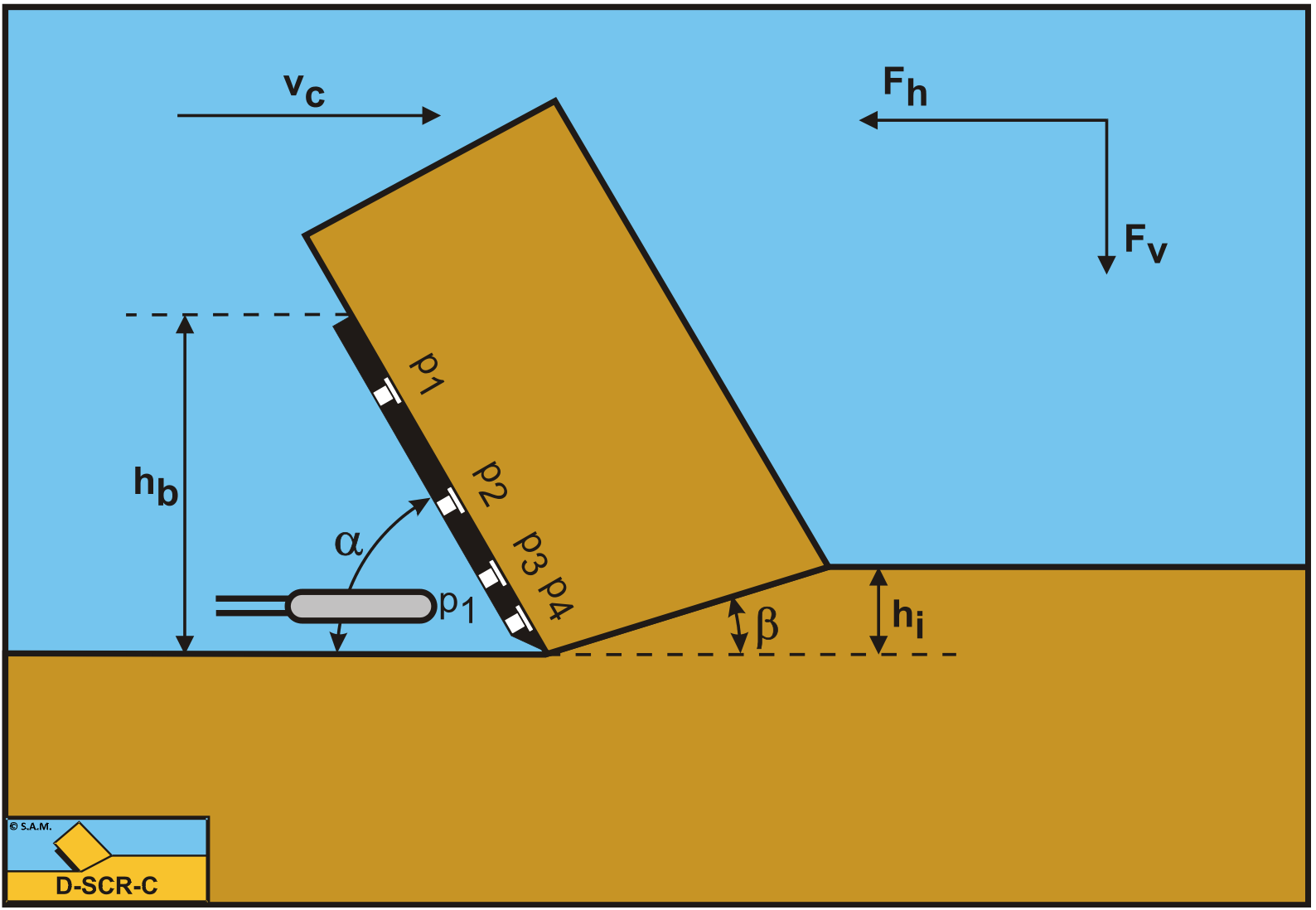
Harder to determine is the angle of internal friction. The following average values for the angle of internal friction are found, for the 200 μm sand:
-
α = 30° » φ = 46.7°
-
α = 45° » φ = 45.9°
-
α = 60° » φ = 41.0°
These values are high above the angle of internal friction that is determined with soil mechanical research according to Appendix K, for a pore percentage of 38.5%. From equation (6-116) it can be derived that the presence of sub-pressure behind the blade makes the angle of internal friction smaller and also that this reduction is larger when the blade angle is smaller. Within the test program space is created to perform experiments where the sub- pressure is measured both on and behind the blade (Figure 6-53). Pressure transducer p1 is removed from the blade and mounted behind the blade tip. Although the number of measurements was too limited to base a theoretical or empirical model on, these measurements have slightly increased the understanding of the sub-pressure behind the blade. Behind the blade tip sub-pressures are measured, with a value of 30% to 60% of the peak pressure on the blade. The highest sub-pressure behind the blade was measured with the 30o blade. This can be explained by the wedge shaped space behind the blade. The following empirical equation gives an estimate of the force W3 based on these measurements:
\[\ \mathrm{W}_{3}=\mathrm{0 .3} \cdot \cot (\alpha) \cdot \mathrm{W}_{2}\tag{6-117}\]
The determination of the angle of internal friction corrected for under pressure behind the blade W3 led to thefollowing values:
-
α = 30° » φ = 36.6°
-
α = 45° » φ = 39.7°
-
α = 60° » φ = 36.8°
For the verification of the cutting tests an average value of 38o for the internal angle of friction is assumed. These values are also more in accordance with the values of internal friction mentioned in Appendix K, where a value of approximate 35o can be found with a pore percentage of 38.5%.
The same phenomena are observed in the determination of the angle of internal friction of the 105 μm sand. The assumption of a hydrostatic pressure behind the blade resulted also in too large values for the angle of internal friction, analogously to the calculations of the 200 μm sand. Here the following values are determined:
-
α = 30° » φ = 46.2°
-
α = 45° » φ = 38.7°
-
α = 60° » φ = 40.3°
The determination of the angle of internal friction corrected for under pressure behind the blade W3 led to the following values:
-
α = 30° » φ = 38.7°
-
α = 45° » φ = 34.0°
-
α = 60° » φ = 38.4°
The low value of the angle of internal friction for the 45o blade can be explained by the fact that these tests are performed for the first time in the new laboratory DE in a situation where the sand was not homogenous from top to bottom. For the verification of the cutting forces and the water pressures is, for both sand types, chosen for a soil/steel friction angle of 30o and an angle of internal friction of 38o, as average values.

