7.2: Introduction
- Page ID
- 29458
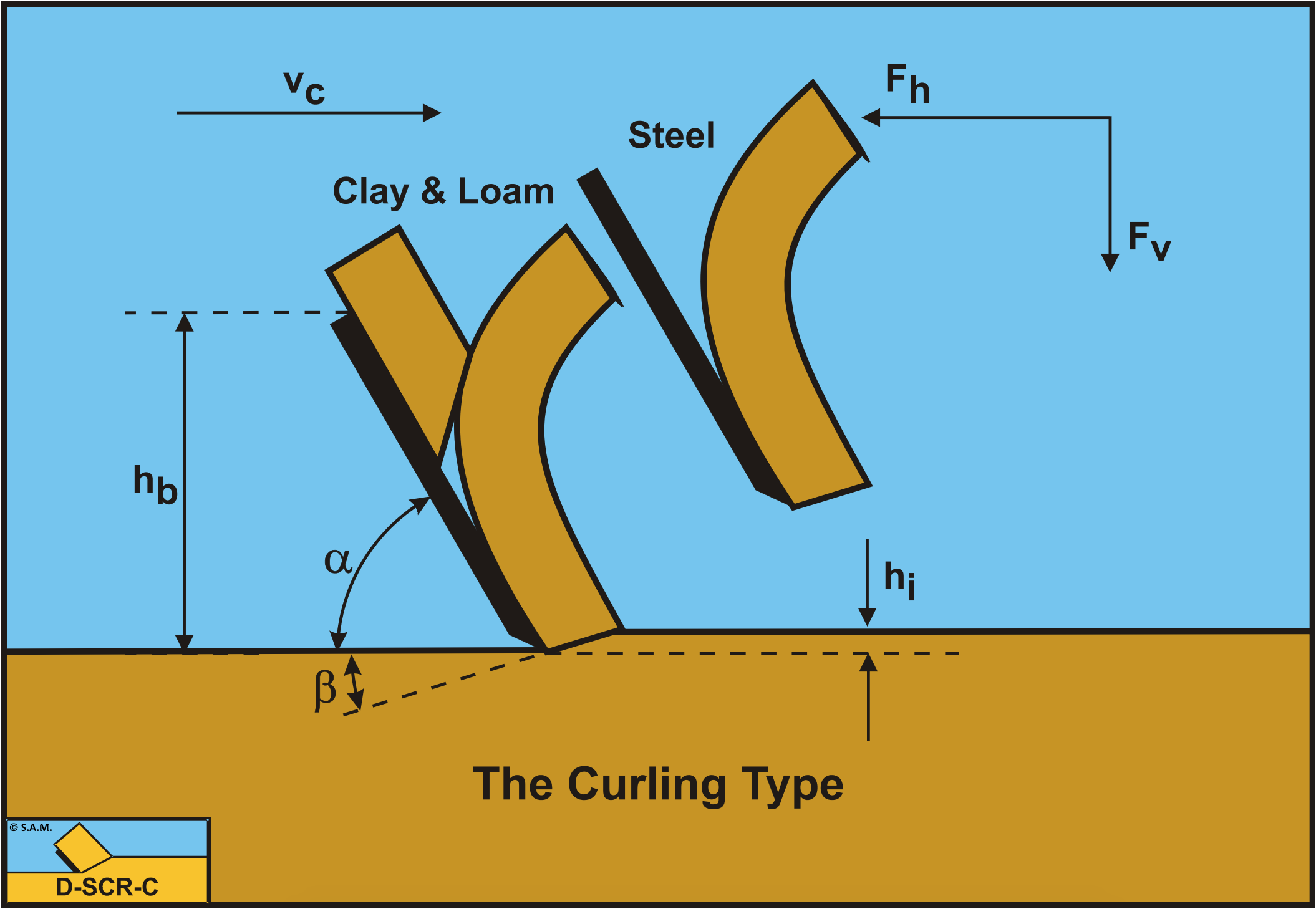
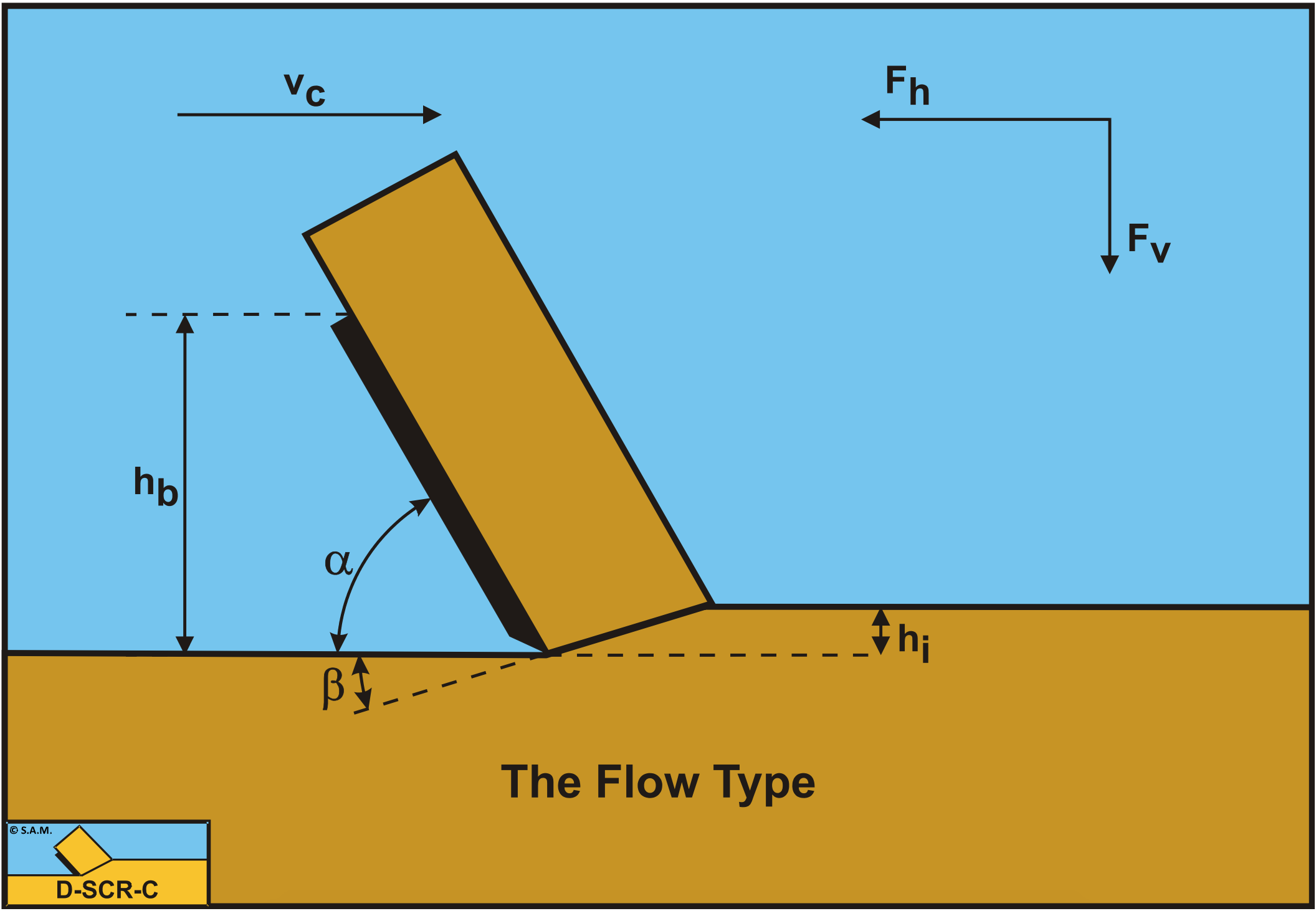
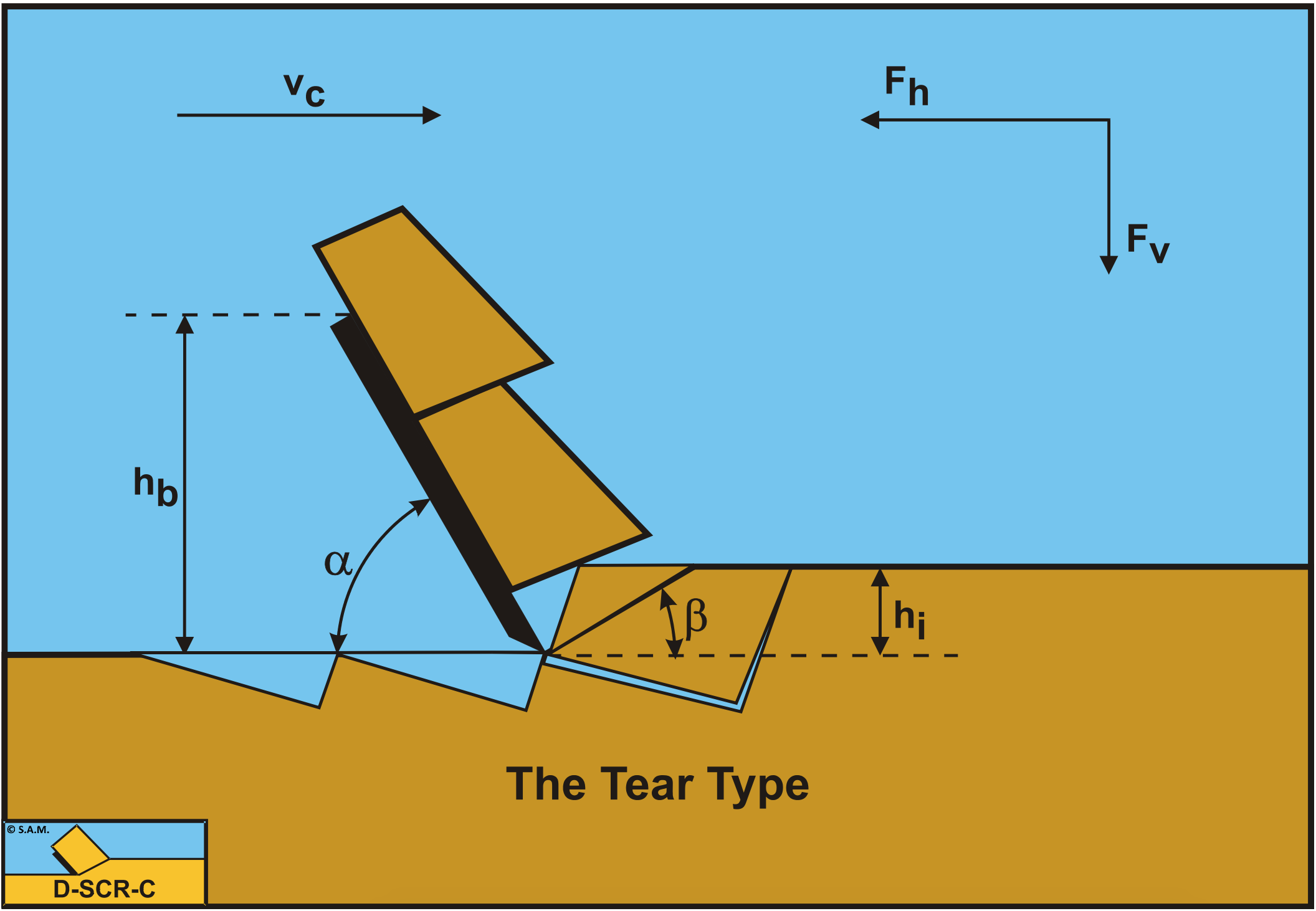
Hatamura and Chijiiwa (1975), (1976A), (1976B), (1977A) and (1977B) distinguished three failure mechanisms in soil cutting. The Shear Type, the Flow Type and the Tear Type. The Flow Type and the Tear Type occur in materials without an angle of internal friction. The Shear Type occurs in materials with an angle of internal friction like sand. A fourth failure mechanism can be distinguished (Miedema (1992)), the Curling Type, as is known in metal cutting. Although it seems that the curling of the chip cut is part of the flow of the material, whether the Curling Type or the Flow Type occurs depends on several conditions. The Curling Type in general will occur if the adhesive force on the blade is large with respect to the normal force on the shear plane. Whether the Curling Type results in pure curling or buckling of the layer cut giving obstruction of the flow depends on different parameters.
Figure 7-2 illustrates the Curling Type mechanism, Figure 7-3 the Flow Type mechanism and Figure 7-4 the Tear Type mechanism as they occur when cutting clay or loam. To predict which type of failure mechanism will occur under given conditions with specific soil, a formulation for the cutting forces has to be derived. The derivation is made under the assumption that the stresses on the shear plane and the blade are constant and equal to the average stresses acting on the surfaces. Figure 7-1 gives some definitions regarding the cutting process. The line A-B is considered to be the shear plane, while the line A-C is the contact area between the blade and the soil. The blade angle is named α and the shear angle β. The blade is moving from left to right with a cutting velocity vc. The thickness of the layer cut is hi and the vertical height of the blade hb. The horizontal force on the blade Fh is positive from right to left always opposite to the direction of the cutting velocity vc. The vertical force on the blade Fv is positive downwards.
Since the vertical force is perpendicular to the cutting velocity, the vertical force does not contribute to the cutting power, which is equal to:
\[\ \mathrm{P}_{\mathrm{c}}=\mathrm{F}_{\mathrm{h}} \cdot \mathrm{v}_{\mathrm{c}}\tag{7-1}\]
In clay the cutting processes are dominated by cohesion and adhesion (internal and external shear strength). Because of the φ=0 concept, the internal and external friction angles are set to 0. Gravity, inertial forces and pore pressures are also neglected. This simplifies the cutting equations. Clay however is subject to strengthening, meaning that the internal and external shear strength increase with an increasing strain rate. The reverse of strengthening is creep, meaning that under a constant load the material will continue deforming with a certain strain rate.
Under normal circumstances clay will be cut with the flow mechanism, but under certain circumstances the Curling Type or the Tear Type may occur.
The Curling Type will occur when the blade height is big with respect to the layer thickness, hb/hi, the adhesion is high compared to the cohesion a/c and the blade angle α is relatively big.
The Tear Type will occur when the blade height is small with respect to the layer thickness, hb/hi, the adhesion is small compared to the cohesion a/c and the blade angle α is relatively small.
This chapter is based on Miedema (1992), (2009) and (2010).


