7.6: The Curling Type
- Page ID
- 29462
7.6.1. Introduction
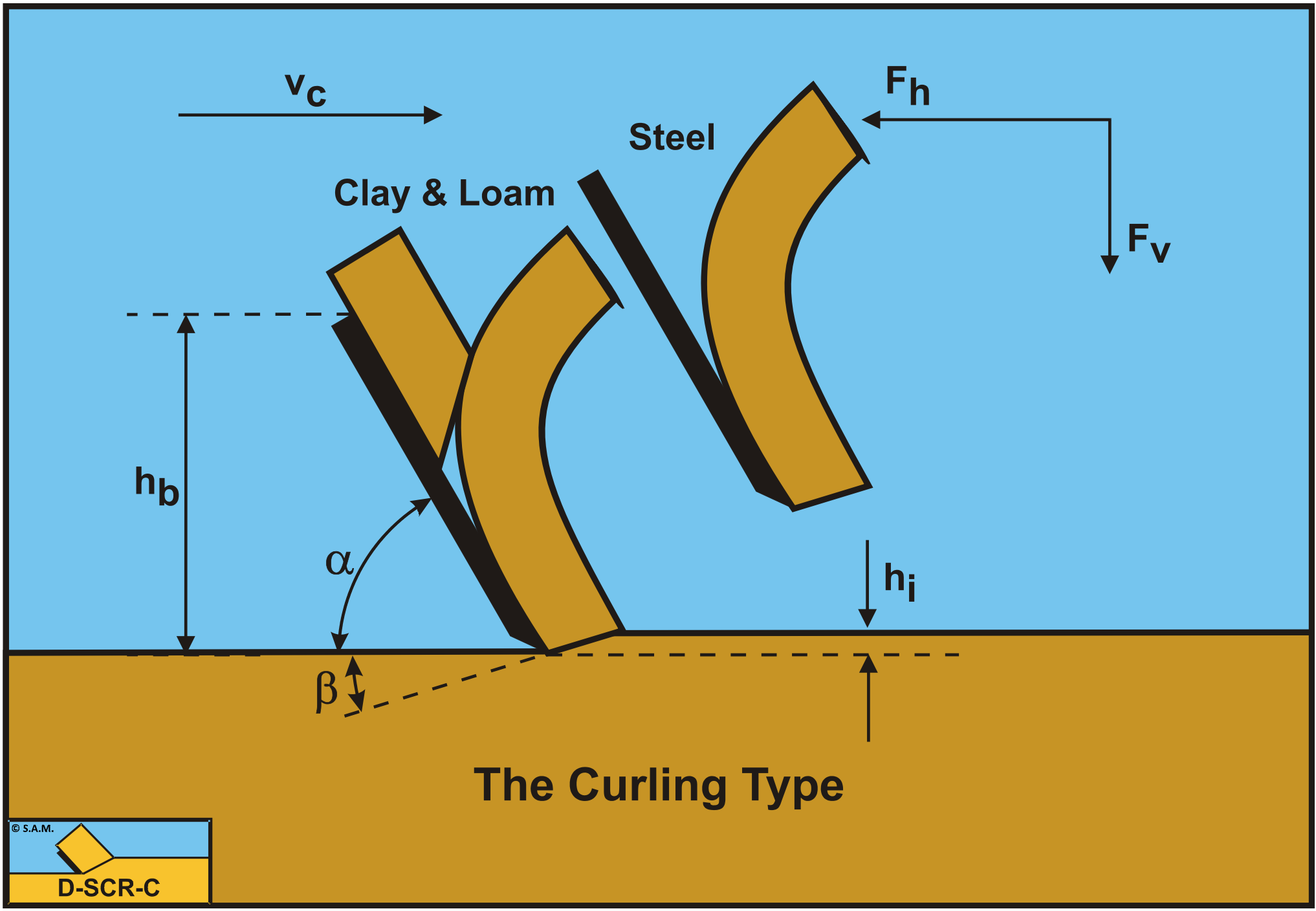
When the layer thickness becomes very small, two things can happen. The normal force on the blade may become negative or there is no equilibrium of moments. In both cases the contact length between the clay and the blade has to be reduced. There can be different mechanisms for this. In steel cutting the curling of the chip cut is well known, but there could also be buckling or breaking of the layer cut. The result is the same, the clay will have a reduced contact length with the blade. This type of cutting mechanism is named the Curling Type. Both the normal force not becoming negative and the equilibrium of moments will be investigated. The mechanism with the smallest cutting forces is assumed to be the correct mechanism.
7.6.2. The Normal Force on the Blade
From the Flow Type of cutting mechanism the following equation is derived for the normal force on the blade:
\[\ \mathrm{N}_{2}=\frac{\mathrm{C}-\mathrm{A} \cdot \cos (\alpha+\beta)}{\sin (\alpha+\beta)}\tag{7-79}\]
Substituting the equations (7-43) and (7-44) gives:
\[\ \begin{array}{left} \mathrm{N}_{2}&= \frac{\frac{\lambda_{\mathrm{s}} \cdot \mathrm{c} \cdot \mathrm{h}_{\mathrm{i}} \cdot \mathrm{w}}{\sin (\beta)}-\frac{\lambda_{\mathrm{s}} \cdot \mathrm{a} \cdot \mathrm{h}_{\mathrm{b}} \cdot \mathrm{w}}{\sin (\alpha)} \cdot \cos (\alpha+\beta)}{\sin (\alpha+\beta)} \\&= \lambda_{\mathrm{s}} \cdot \mathrm{c} \cdot \mathrm{h}_{\mathrm{i}} \cdot \mathrm{w} \cdot \frac{\frac{1}{\sin (\beta)}-\frac{\mathrm{r}}{\sin (\alpha)} \cdot \cos (\alpha+\beta)}{\sin (\alpha+\beta)} \end{array}\tag{7-80}\]
Dividing the normal force by the surface of the blade gives the average normal stress on the blade:
\[\ \sigma_{\mathrm{N} 2}=\frac{\mathrm{N}_{2} \cdot \sin (\alpha)}{\mathrm{h}_{\mathrm{b}} \cdot \mathrm{w}}\tag{7-81}\]
This gives for the normal stress on the blade:
\[\ \begin{array}{left} \sigma_{\mathrm{N} 2}&= \frac{\sin (\alpha)}{\mathrm{h}_{\mathrm{b}} \cdot \mathrm{w}} \cdot \frac{\frac{\lambda_{\mathrm{s}} \cdot \mathrm{c} \cdot \mathrm{h}_{\mathrm{i}} \cdot \mathrm{w}}{\sin (\beta)}-\frac{\lambda_{\mathrm{s}} \cdot \mathrm{a} \cdot \mathrm{h}_{\mathrm{b}} \cdot \mathrm{w}}{\sin (\alpha)} \cdot \cos (\alpha+\beta)}{\sin (\alpha+\beta)} \\&= \lambda_{\mathrm{s}} \cdot \mathrm{a} \cdot \frac{\frac{1}{\mathrm{r}} \cdot \frac{\sin (\alpha)}{\sin (\beta)}-\cos (\alpha+\beta)}{\sin (\alpha+\beta)} \end{array}\tag{7-82}\]
As stated before this normal stress should have a value greater than zero, since it is assumed that there is no tensile strength between the clay and the blade.
\[\ \sigma_{\mathrm{N} 2} \geq 0\tag{7-83}\]
In details this gives for the condition of no negative normal stress on the blade:
\[\ \lambda_{\mathrm{s}} \cdot \mathrm{a} \cdot \frac{\frac{1}{\mathrm{r}} \cdot \frac{\sin (\alpha)}{\sin (\beta)}-\cos (\alpha+\beta)}{\sin (\alpha+\beta)} \geq 0\tag{7-84}\]
At the critical condition where the normal stress equals zero this gives:
\[\ \frac{1}{\mathrm{r}} \cdot \frac{\sin (\alpha)}{\sin (\beta)}=\cos (\alpha+\beta)\tag{7-85}\]
In the case of the Curling Type, the ac ratio r is not fully mobilized giving:
\[\ \mathrm{r_{m}}=\frac{\sin (\alpha)}{\sin (\beta)} \cdot \frac{1}{\cos (\alpha+\beta)}\tag{7-86}\]
Substituting this mobilized ac ratio rm in equations (7-46) and (7-47) gives for the cutting forces:
\[\ \begin{array}{left}\mathrm{F_{\mathrm{h}}}&=\lambda_{\mathrm{s}} \cdot \mathrm{c} \cdot \mathrm{h_{\mathrm{i}}} \cdot \mathrm{w} \cdot \frac{\frac{\sin (\alpha)}{\sin (\beta)}+\mathrm{r}_{\mathrm{m}} \cdot \frac{\sin (\beta)}{\sin (\alpha)}}{\sin (\alpha+\beta)}=\lambda_{\mathrm{s}} \cdot \mathrm{c} \cdot \mathrm{h_{\mathrm{i}}} \cdot \mathrm{w} \cdot \frac{\frac{\sin (\alpha)}{\sin (\beta)}+\frac{1}{\cos (\alpha+\beta)}}{\sin (\alpha+\beta)}\\
&=\lambda_{\mathrm{s}} \cdot \mathrm{c} \cdot \mathrm{h}_{\mathrm{i}} \cdot \mathrm{w} \cdot \frac{\frac{\cos (\alpha)}{\sin (\beta)}}{\cos (\alpha+\beta)}\end{array}\tag{7-87}\]
\[\ \begin{array}{left}\mathrm{F}_{v}&=\mathrm{\lambda_{s} \cdot c \cdot h_{i} \cdot w \cdot \frac{\frac{\cos (\alpha)}{\sin (\beta)}-r_{m} \cdot \frac{\cos (\beta)}{\sin (\alpha)}}{\sin (\alpha+\beta)}=\lambda_{s} \cdot c \cdot h_{i} \cdot w \cdot \frac{\frac{\cos (\alpha)}{\sin (\beta)}-\frac{\cos (\beta)}{\sin (\beta)} \cdot \frac{1}{\cos (\alpha+\beta)}}{\sin (\alpha+\beta)}}\\
&=\mathrm{-\lambda_{s} \cdot c \cdot h_{i} \cdot w \cdot \frac{\frac{\sin (\alpha)}{\sin (\beta)}}{\cos (\alpha+\beta)}}\end{array}\tag{7-88}\]
This method is simple and straightforward, but does not take a normal stress distribution on the blade into account. It does however give a prediction of the cutting forces and the reduced contact length on the blade. The unknown in the equations is the shear angle β. Assuming that the mechanism will choose a shear angle where the cutting energy is at a minimum, a shear angle β is found according to:
\[\ \beta=\frac{\pi}{4}-\frac{\alpha}{2}\tag{7-89}\]
If we substitute this solution in the cutting force equations we find:
\[\ \mathrm{F_{h}=2 \cdot \lambda_{s} \cdot c \cdot h_{i} \cdot w \cdot \frac{\cos (\alpha)}{1-\sin (\alpha)}}\tag{7-90}\]
\[\ \mathrm{F}_{v}=\mathrm{-2 \cdot \lambda_{s} \cdot c \cdot h_{i} \cdot w \cdot \frac{\sin (\alpha)}{1-\sin (\alpha)}}\tag{7-91}\]
The horizontal force will increase with an increasing blade angle, the vertical force also, but upwards directed. In the case of the Curling Type, the ac ratio r is not fully mobilized giving:
\[\ \mathrm{r_{m}=2 \cdot \frac{\sin (\alpha)}{1-\sin (\alpha)}}\tag{7-92}\]
The condition of having a normal force of zero on the blade can never fulfill the condition of having an equilibrium of moments on the layer cut, since the normal force on the blade is zero and is therefore rejected. Still this condition gives insight in the behavior of the equations of clay cutting and is therefore mentioned here.
7.6.3. The Equilibrium of Moments
As mentioned in the previous paragraph, the equilibrium of moments on the layer cut has to be fulfilled. If we take the equilibrium of moments around the tip of the blade, there are only two forces participating in the equilibrium of moments, the normal force on the shear plane N1 and the normal force on the blade N2. These forces have acting points R1 and R2 on the shear plane and on the blade. If the normal stresses are uniformly distributed, both acting points will be at the center (half way) the corresponding planes. The acting point of the normal force on the shear plane will be at half the length of the shear plane and the acting point of the normal force on the blade will be at half the (mobilized) length of the blade. Two factors are introduced to give the exact location of these acting points, λ1 on the shear plane and λ2 on the blade. When the moment N2·R2 on the blade is greater than the moment N1·R1 on the blade curling will occur in such a way that both moments are equal. The contact length between the clay and the blade will be reduced to a mobilized contact length hb,m.
The normal force on the shear plane is now equal to the force N1, because the internal friction angle is zero:
\[\ \mathrm{N}_{1}=\frac{-\mathrm{C} \cdot \cos (\alpha+\beta)+\mathrm{A}}{\sin (\alpha+\beta)}\tag{7-93}\]
The normal force on the blade is now equal to the force N2, because the external friction angle is zero:
\[\ \mathrm{N}_{2}=\frac{\mathrm{C}-\mathrm{A} \cdot \cos (\alpha+\beta)}{\sin (\alpha+\beta)}\tag{7-94}\]
This gives for the equilibrium of moments:
\[\ \mathrm{N}_{1} \cdot \mathrm{R}_{1}=\mathrm{N}_{2} \cdot \mathrm{R}_{2}\tag{7-95}\]
For both acting points we can write:
\[\ \mathrm{R_{1}=\frac{\lambda_{1} \cdot h_{\mathrm{i}}}{\sin (\beta)}, R_{2}=\frac{\lambda_{2} \cdot h_{\mathrm{b}, \mathrm{m}}}{\sin (\alpha)}}\tag{7-96}\]
Substituting equations (7-93), (7-94) and (7-96) in equation (7-95) gives:
\[\ \left(\frac{\mathrm{A}-\mathrm{C} \cdot \cos (\alpha+\beta)}{\sin (\alpha+\beta)}\right) \cdot \frac{\lambda_{1} \cdot \mathrm{h}_{\mathrm{i}}}{\sin (\beta)}=\left(\frac{\mathrm{C}-\mathrm{A} \cdot \cos (\alpha+\beta)}{\sin (\alpha+\beta)}\right) \cdot \frac{\lambda_{2} \cdot \mathrm{h}_{\mathrm{b}, \mathrm{m}}}{\sin (\alpha)}\tag{7-97}\]
Substituting equations (7-45) and (7-46) for the cohesive and adhesive forces gives:
\[\ \left(\frac{\mathrm{a} \cdot \mathrm{h}_{\mathrm{b}, \mathrm{m}}}{\sin (\alpha)}-\frac{\mathrm{c} \cdot \mathrm{h}_{\mathrm{i}}}{\sin (\beta)} \cdot \cos (\alpha+\beta)\right) \cdot \frac{\lambda_{1} \cdot \mathrm{h}_{\mathrm{i}}}{\sin (\beta)}=\left(\frac{\mathrm{c} \cdot \mathrm{h}_{\mathrm{i}}}{\sin (\beta)}-\frac{\mathrm{a} \cdot \mathrm{h}_{\mathrm{b}, \mathrm{m}}}{\sin (\alpha)} \cdot \cos (\alpha+\beta)\right) \cdot \frac{\lambda_{2} \cdot \mathrm{h}_{\mathrm{b}, \mathrm{m}}}{\sin (\alpha)}\tag{7-98}\]
Rewriting this term by term gives:
\[\ \frac{\mathrm{a} \cdot \mathrm{h}_{\mathrm{b}, \mathrm{m}}}{\sin (\alpha)} \cdot \frac{\lambda_{1} \cdot \mathrm{h}_{\mathrm{i}}}{\sin (\beta)}-\frac{\mathrm{c} \cdot \mathrm{h}_{\mathrm{i}}}{\sin (\beta)} \cdot \frac{\lambda_{1} \cdot \mathrm{h}_{\mathrm{i}}}{\sin (\beta)} \cdot \cos (\alpha+\beta)=\frac{\mathrm{c} \cdot \mathrm{h}_{\mathrm{i}}}{\sin (\beta)} \cdot \frac{\lambda_{2} \cdot \mathrm{h}_{\mathrm{b}, \mathrm{m}}}{\sin (\alpha)}-\frac{\mathrm{a} \cdot \mathrm{h}_{\mathrm{b}, \mathrm{m}}}{\sin (\alpha)} \cdot \frac{\lambda_{2} \cdot \mathrm{h}_{\mathrm{b}, \mathrm{m}}}{\sin (\alpha)} \cdot \cos (\alpha+\beta)\tag{7-99}\]
Moving the terms with adhesion to the left side and the terms with cohesion to the right side gives:
\[\ \frac{\mathrm{a} \cdot \mathrm{h}_{\mathrm{b}, \mathrm{m}}}{\sin (\alpha)} \cdot \frac{\lambda_{1} \cdot \mathrm{h}_{\mathrm{i}}}{\sin (\beta)}+\frac{\mathrm{a} \cdot \mathrm{h}_{\mathrm{b}, \mathrm{m}}}{\sin (\alpha)} \cdot \frac{\lambda_{2} \cdot \mathrm{h}_{\mathrm{b}, \mathrm{m}}}{\sin (\alpha)} \cdot \cos (\alpha+\beta)=\frac{\mathrm{c} \cdot \mathrm{h}_{\mathrm{i}}}{\sin (\beta)} \cdot \frac{\lambda_{2} \cdot \mathrm{h}_{\mathrm{b}, \mathrm{m}}}{\sin (\alpha)}+\frac{\mathrm{c} \cdot \mathrm{h}_{\mathrm{i}}}{\sin (\beta)} \cdot \frac{\lambda_{1} \cdot \mathrm{h}_{\mathrm{i}}}{\sin (\beta)} \cdot \cos (\alpha+\beta)\tag{7-100}\]
This gives a second degree function of the mobilized blade height according to:
\[\ \frac{\lambda_{2} \cdot \mathrm{a} \cdot \cos (\alpha+\beta)}{\sin (\alpha) \cdot \sin (\alpha)} \cdot \mathrm{h}_{\mathrm{b}, \mathrm{m}} \cdot \mathrm{h}_{\mathrm{b}, \mathrm{m}}+\frac{\lambda_{1} \cdot \mathrm{a}-\lambda_{2} \cdot \mathrm{c}}{\sin (\alpha) \cdot \sin (\beta)} \cdot \mathrm{h}_{\mathrm{i}} \cdot \mathrm{h}_{\mathrm{b}, \mathrm{m}}-\frac{\lambda_{1} \cdot \mathrm{c} \cdot \cos (\alpha+\beta)}{\sin (\beta) \cdot \sin (\beta)} \cdot \mathrm{h}_{\mathrm{i}} \cdot \mathrm{h}_{\mathrm{i}}=\mathrm{0}\tag{7-101}\]
This second degree function can be solved with the A, B, C formula and has two solutions.
\[\ \begin{array}{left}\mathrm{A} \cdot \mathrm{x}^{2}+\mathrm{B} \cdot \mathrm{x}+\mathrm{C}=\mathrm{0}\\
\mathrm{h}_{\mathrm{b}, \mathrm{m}}=\mathrm{x}=\frac{-\mathrm{B} \pm \sqrt{\mathrm{B}^{2}-\mathrm{4} \cdot \mathrm{A} \cdot \mathrm{C}}}{\mathrm{2A}} \quad\text{with: } \mathrm{r}_{\mathrm{m}}=\frac{\mathrm{a} \cdot \mathrm{h}_{\mathrm{b}, \mathrm{m}}}{\mathrm{c} \cdot \mathrm{h}_{\mathrm{i}}}\\
\mathrm{A}=\frac{\lambda_{2} \cdot \mathrm{a} \cdot \cos (\alpha+\beta)}{\sin (\alpha) \cdot \sin (\alpha)}\\
\mathrm{B}=\frac{\lambda_{1} \cdot \mathrm{a}-\lambda_{2} \cdot \mathrm{c}}{\sin (\alpha) \cdot \sin (\beta)} \cdot \mathrm{h}_{\mathrm{i}}\\
\mathrm{C}=-\frac{\lambda_{1} \cdot \mathrm{c} \cdot \cos (\alpha+\beta)}{\sin (\beta) \cdot \sin (\beta)} \cdot \mathrm{h}_{\mathrm{i}} \cdot \mathrm{h}_{\mathrm{i}}\end{array}\tag{7-102}\]
The following criteria are valid for the use of this method.
\[\ \begin{array}{left} \text{if } \mathbf{h}_{\mathbf{b}, \mathbf{m}}<\mathbf{h}_{\mathbf{b}}\text{ then use }\mathbf{h}_{\mathbf{b}, \mathbf{m}}\\
\text{if }\mathbf{h}_{\mathbf{b}, \mathbf{m}} \geq \mathbf{h}_{\mathbf{b}}\text{ then use }\mathbf{h}_{\mathbf{b}, \mathbf{m}}\end{array}\tag{7-103}\]
To see which solution is valid, the terms of the equation have to be analyzed. For α+β<π/2 the term A>0 and C<0 because of the minus sign. The term B is always positive. This will only result in a positive solution if the + sign is applied. For α+β>π/2 the term A<0 and C>0 because of the minus sign. This will only result in a positive solution if the – sign is applied. So at small blade angles the plus sign gives the correct solution, while large blade angles require the minus sign solution.
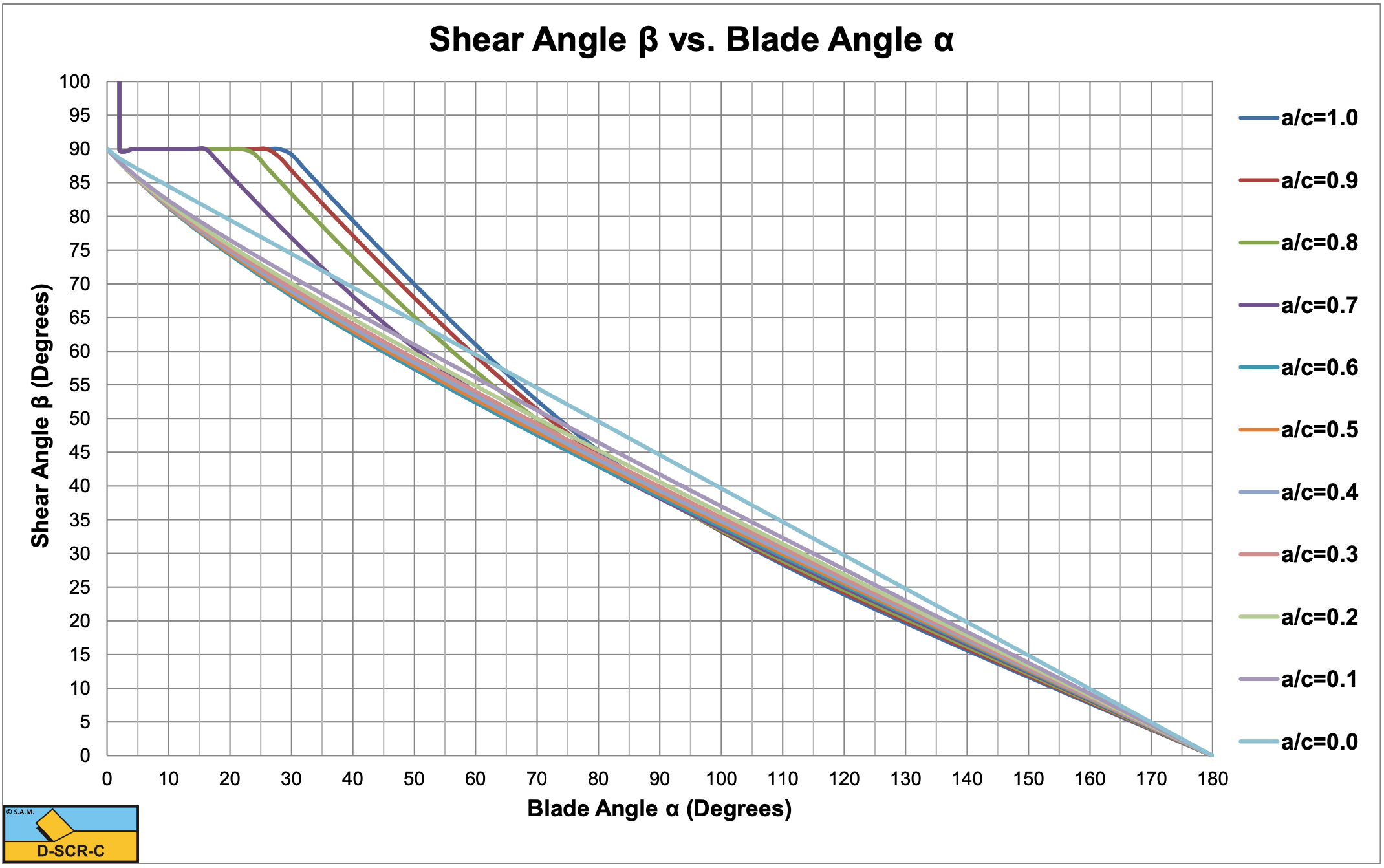
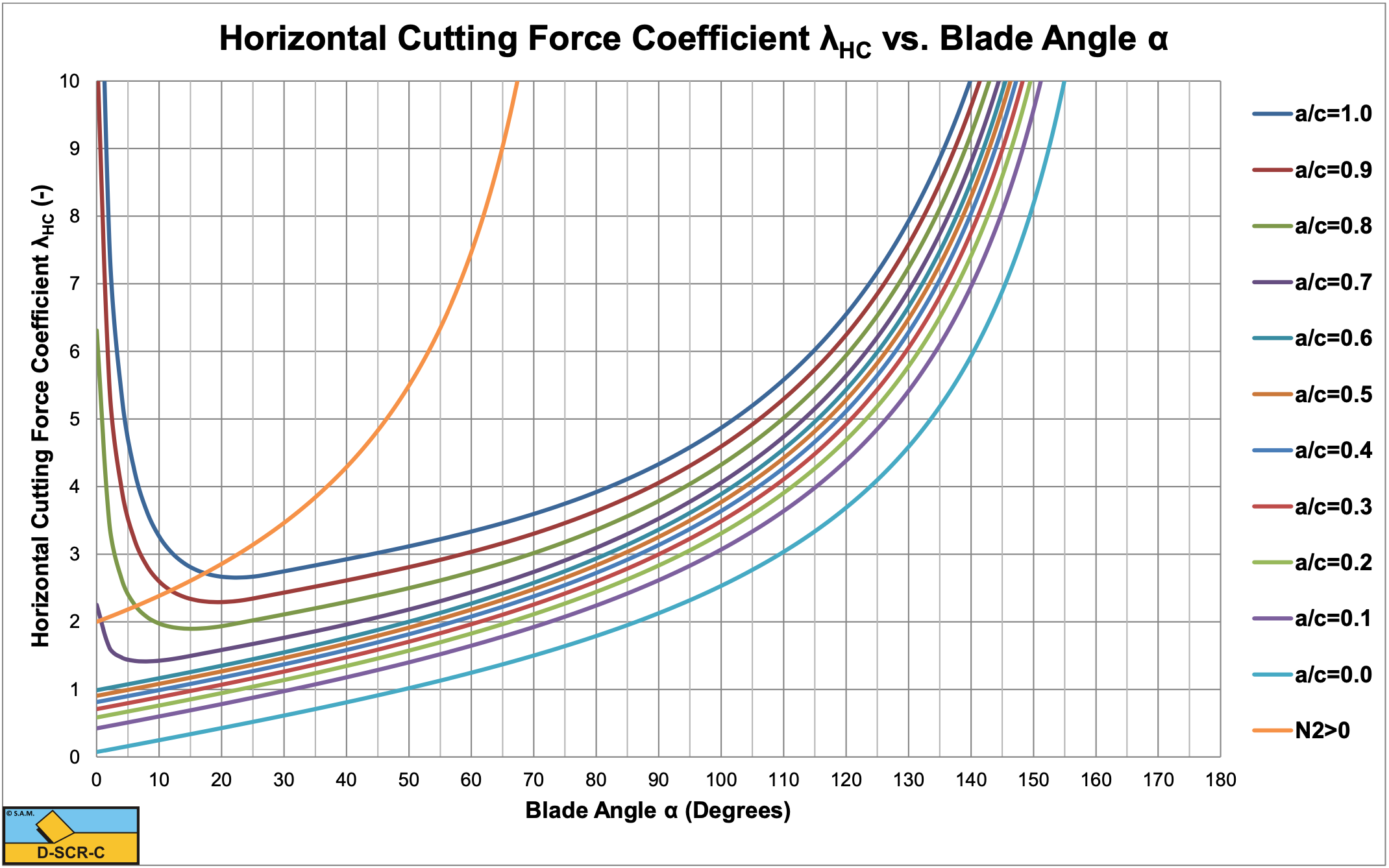
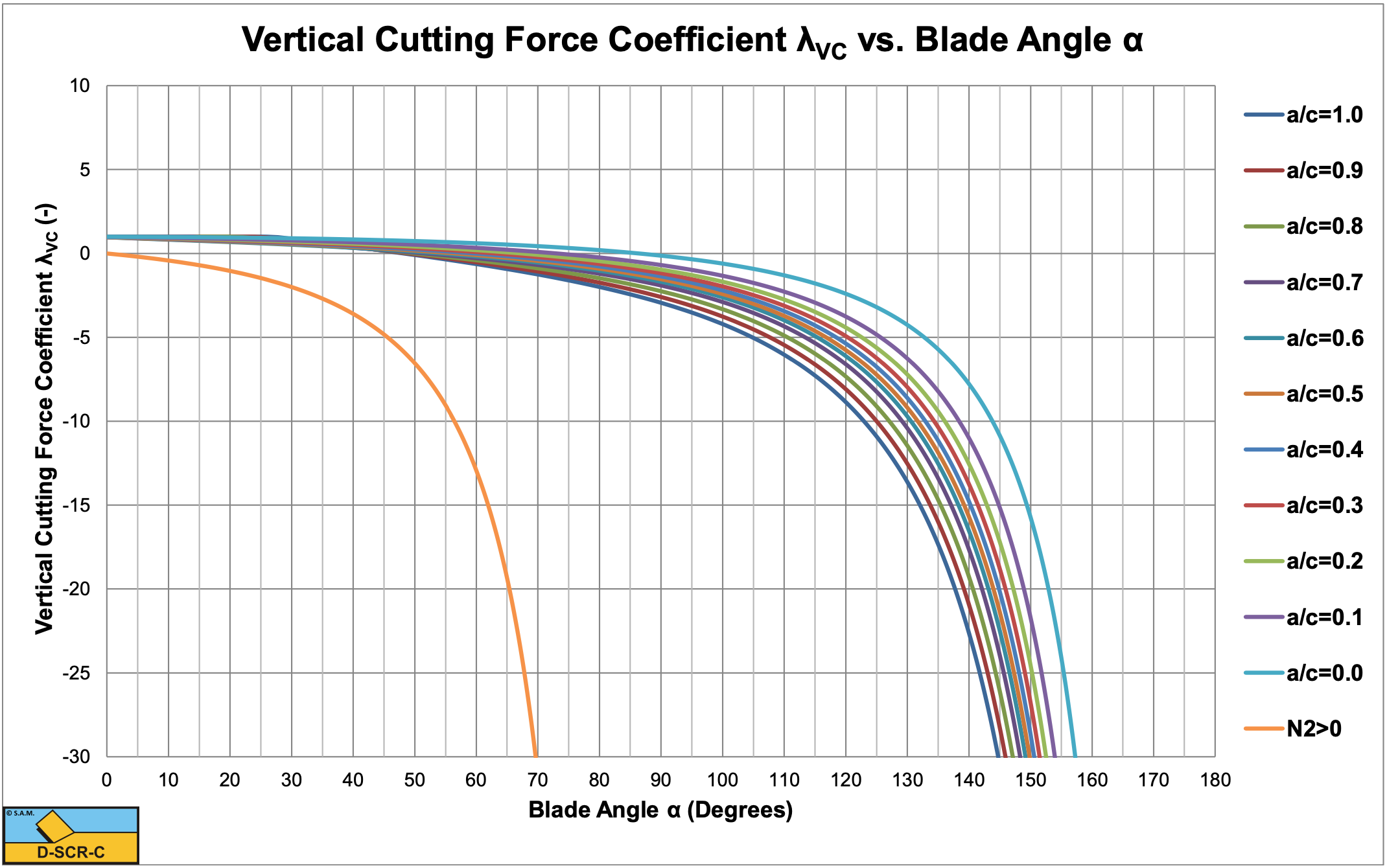
Figure 7-35, Figure 7-36 and Figure 7-37 show the shear angle and the horizontal cutting force coefficient and the vertical cutting force coefficient for the Curling Type. At large blade angles, both the horizontal and vertical forces become very large. In cases of large blade angles the Curling Type will hardly occur because the Flow Type results in smaller forces.
\[\ \mathrm{F_{\mathrm{h}}=\lambda_{\mathrm{s}} \cdot \mathbf{c} \cdot \mathbf{h}_{\mathrm{i}} \cdot \mathbf{w} \cdot \frac{\frac{\sin (\alpha)}{\sin (\beta)}+r_{\mathrm{m}} \cdot \frac{\sin (\beta)}{\sin (\alpha)}}{\sin (\alpha+\beta)}=\lambda_{\mathrm{s}} \cdot \mathbf{c} \cdot \mathbf{h}_{\mathrm{i}} \cdot \mathbf{w} \cdot \lambda_{\mathrm{HC}}}\tag{7-104}\]
\[\ \mathrm{F}_{v}=\mathrm{\lambda_{s} \cdot c \cdot h_{i} \cdot w \cdot \frac{\frac{\cos (\alpha)}{\sin (\beta)}-r_{m} \cdot \frac{\cos (\beta)}{\sin (\alpha)}}{\sin (\alpha+\beta)}=\lambda_{s} \cdot c \cdot h_{i} \cdot w \cdot \lambda_{V C}}\tag{7-105}\]

Figure 7-35, Figure 7-36 and Figure 7-37 clearly show the transition from the plus root solution to the minus root solution. This transition results in a discontinuity. How exactly this transition will take place in nature is still subject for further research. Confidential tests in clay with blade angles of 20, 30 and 40 degrees have shown that the plus root solution is valid at small blade angles, tests in hyperbaric rock cutting with a blade angle of 110 degrees have shown that the minus root solution is valid at large blade angles (see Chapter 9:). One should consider that the Curling Type only occurs with thin layers. Once the required mobilized blade height exceeds the actual blade height, the Flow Type will occur. So for example, if blade height and layer thickness are equal, the ratio cannot exceed 1 and depending on the a/c ratio, the Flow Type will occur above a certain blade angle.