8.4: The Flow Type (Based on the Merchant Model)
- Page ID
- 29467
Rock is the collection of materials where the grains are bonded chemically from very stiff clay, sandstone to very hard basalt. It is difficult to give one definition of rock or stone and also the composition of the material can differ strongly. Still it is interesting to see if the model used for sand and clay, which is based on the Coulomb model, can be used for rock as well. Typical parameters for rock are the compressive strength UCS and the tensile strength BTS and specifically the ratio between those two, which is a measure for how fractured the rock is. Rock also has shear strength and because it consists of bonded grains it will have an internal friction angle and an external friction angle. It can be assumed that the permeability of the rock is very low, so initially the pore pressures do no play a role or cavitation will always occur under atmospheric conditions. But since the absolute hydrostatic pressure, which would result in a cavitation under pressure of the same magnitude can be neglected with respect to the compressive strength of the rock; the pore pressures are usually neglected. This results in a material where gravity, inertia, pore pressures and adhesion can be neglected.
Merchant (1944), (1945A) and (1945B) derived a model for determining the cutting forces when machining steel. The model was based on plastic deformation and a continuous chip formation (ductile cutting). The model included internal and external friction and shear strength, but no adhesion, gravity, inertia and pore pressures. Later Miedema (1987 September) extended this model with adhesion, gravity, inertial forces and pore water pressures.
Definitions:
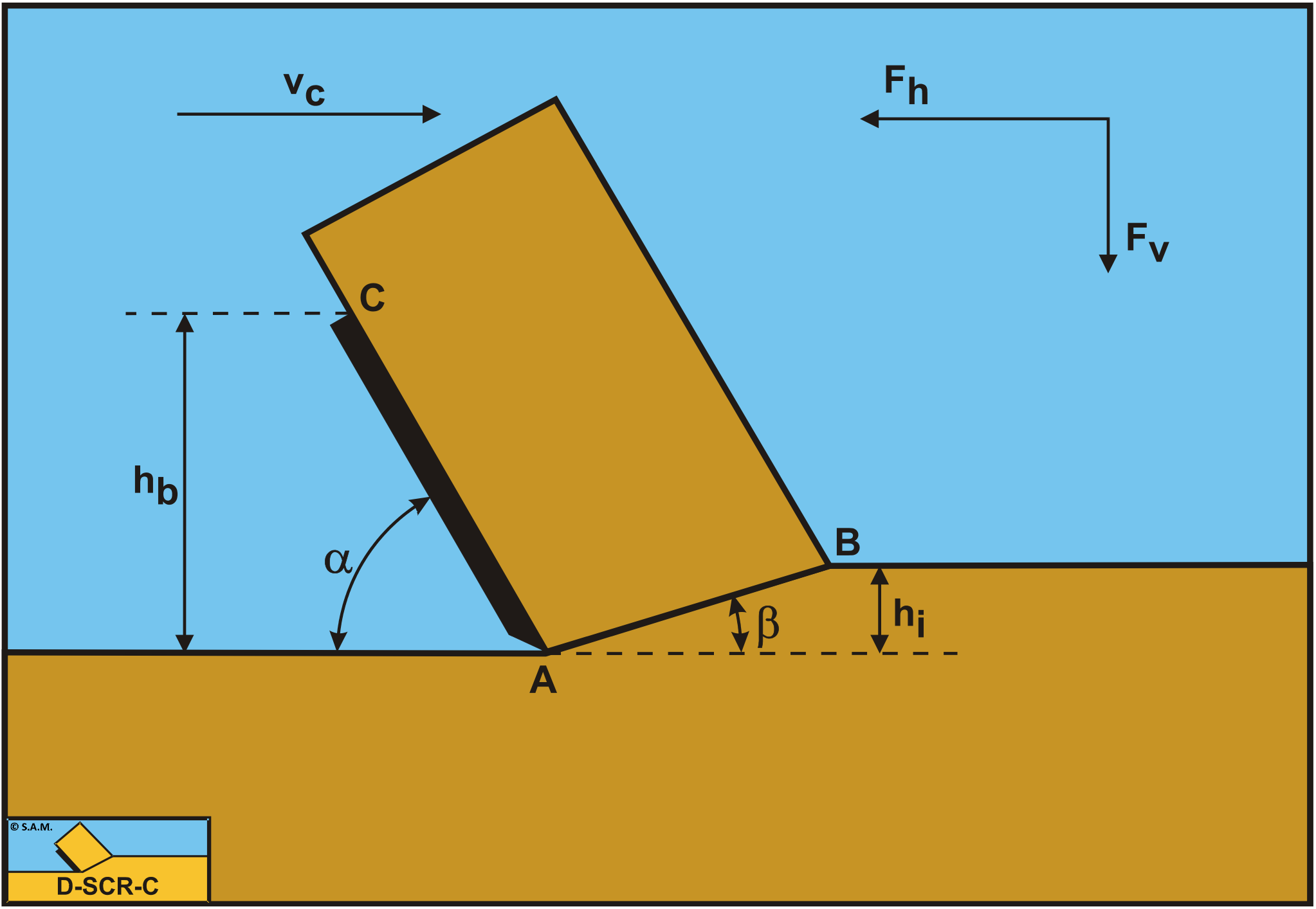
-
A: The blade tip.
-
B: End of the shear plane.
-
C: The blade top.
-
A-B: The shear plane.
-
A-C: The blade surface.
-
hb: The height of the blade.
-
hi: The thickness of the layer cut.
-
vc: The cutting velocity.
-
α: The blade angle.
-
β: The shear angle.
-
Fh: The horizontal force, the arrow gives the positive direction.
-
Fv: The vertical force, the arrow gives the positive direction.
Figure 8-26 gives some definitions regarding the cutting process. The line A-B is considered to be the shear plane, while the line A-C is the contact area between the blade and the soil. The blade angle is named α and the shear angle β. The blade is moving from left to right with a cutting velocity vc. The thickness of the layer cut is hi and the vertical height of the blade hb. The horizontal force on the blade Fh is positive from right to left always opposite to the direction of the cutting velocity vc. The vertical force on the blade Fv is positive downwards. Since the vertical force is perpendicular to the cutting velocity, the vertical force does not contribute to the cutting power Pc, which is equal to:
\[\ \mathrm{P}_{\mathrm{c}}=\mathrm{F}_{\mathrm{h}} \cdot \mathrm{v}_{\mathrm{c}}\tag{8-96}\]
The specific energy Esp is defined as the amount of energy used/required to excavate 1 m3 of soil/rock. This can be determined by dividing the cutting power Pc by the production Q and results in the cutting force Fh in the direction of the cutting velocity vc, divided by the cross section cut hi·w:
\[\ \mathrm{E}_{\mathrm{sp}}=\frac{\mathrm{P}_{\mathrm{c}}}{\mathrm{Q}}=\frac{\mathrm{F}_{\mathrm{h}} \cdot \mathrm{v}_{\mathrm{c}}}{\mathrm{h}_{\mathrm{i}} \cdot \mathrm{w} \cdot \mathrm{v}_{\mathrm{c}}}=\frac{\mathrm{F}_{\mathrm{h}}}{\mathrm{h}_{\mathrm{i}} \cdot \mathrm{w}}\tag{8-97}\]
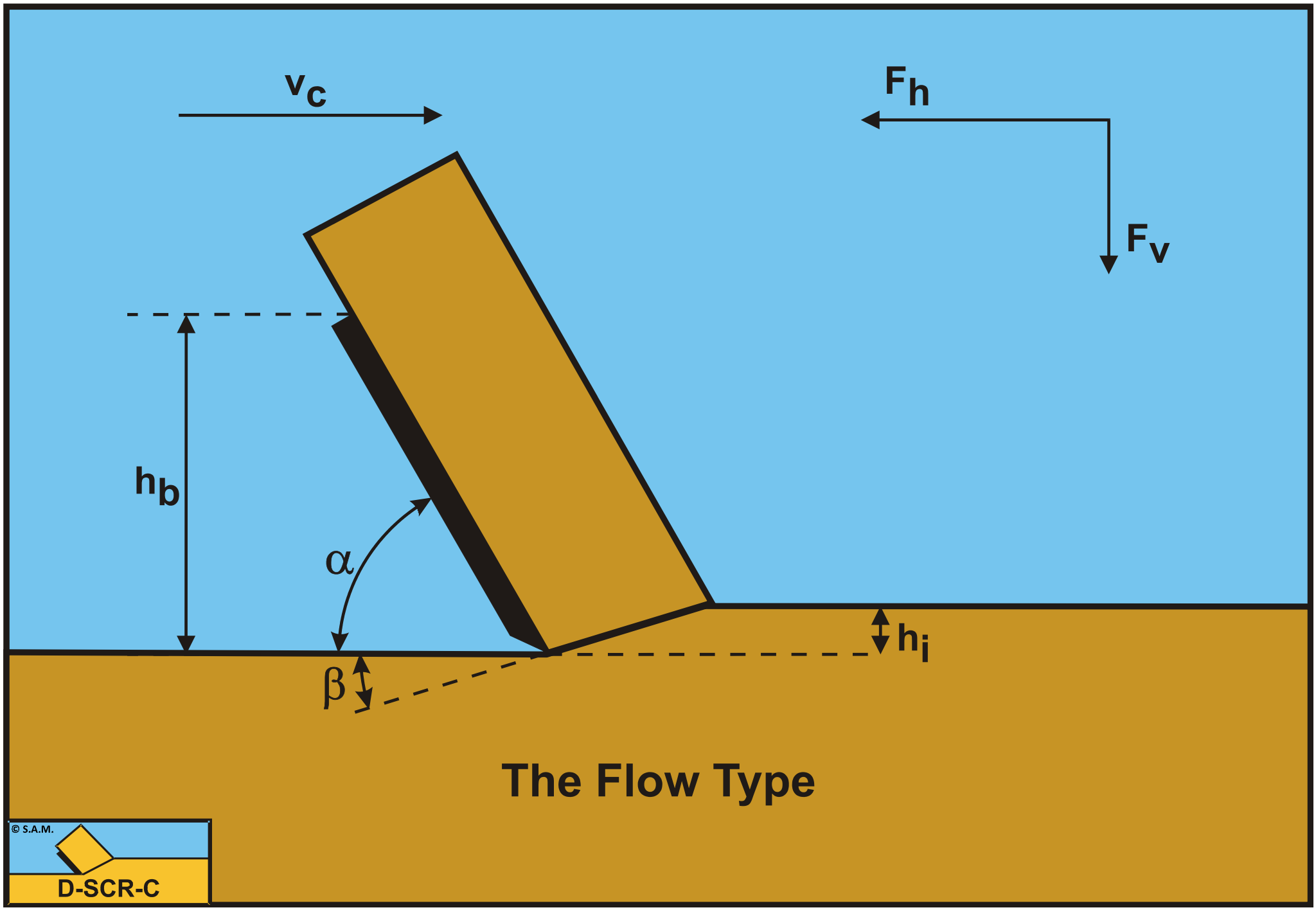
The model for rock cutting under atmospheric conditions is based on the Flow Type of cutting mechanism. Although in general rock will encounter a more brittle failure mechanism and the Flow Type considered represents the ductile failure mechanism, the Flow Type mechanism forms the basis for all cutting processes. The definitions of the Flow Type mechanism are shown in Figure 8-27.
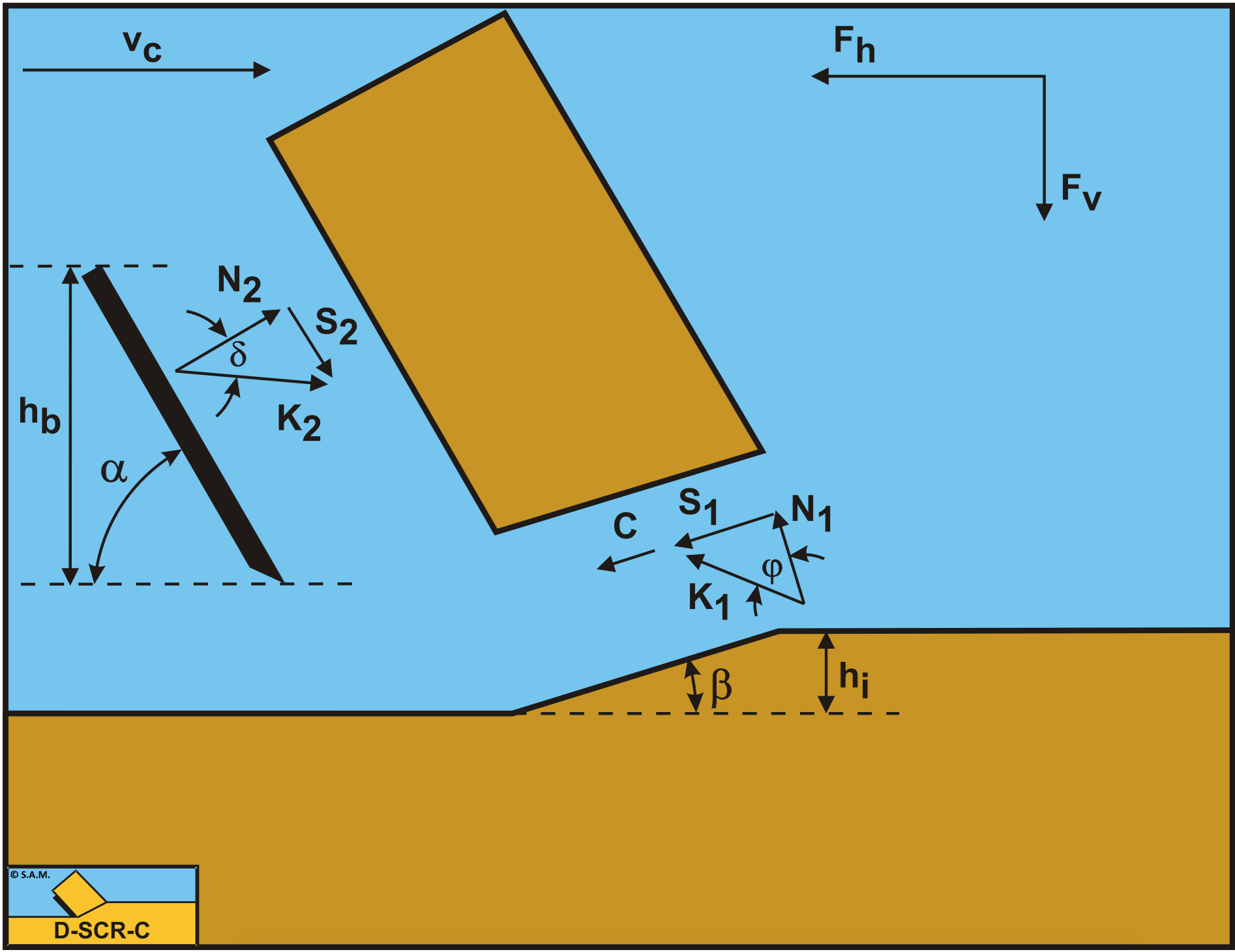
Figure 8-28 illustrates the forces on the layer of rock cut. The forces shown are valid in general. The forces acting on this layer are:
-
A normal force acting on the shear surface N1 resulting from the grain stresses.
-
A shear force S1 as a result of internal friction N1·tan(φ).
-
A shear force C as a result of the shear strength (cohesion) \(\ \tau\)c or c. This force can be calculated by multiplying the cohesive shear strength \(\ \tau\)c with the area of the shear plane.
-
A force normal to the blade N2 resulting from the grain stresses.
-
A shear force S2 as a result of the soil/steel friction N2·tan(δ) or external friction.
The normal force N1 and the shear force S1 can be combined to a resulting grain force K1.
The forces acting on a straight blade when cutting rock, can be distinguished as:
-
A force normal to the blade N2 resulting from the grain stresses.
-
A shear force S2 as a result of the soil/steel friction N2·tan(δ) or external friction.
These forces are shown in Figure 8-29. If the forces N2 and S2 are combined to a resulting force K2 the resulting force K2 is the unknown force on the blade. By taking the horizontal and vertical equilibrium of forces an expression for the force K2 on the blade can be derived.
The horizontal equilibrium of forces:
\[\ \sum \mathrm{F}_{\mathrm{h}}=\mathrm{K}_{\mathrm{1}} \cdot \sin (\beta+\varphi)+\mathrm{C} \cdot \cos (\beta)-\mathrm{K}_{2} \cdot \sin (\alpha+\delta)=\mathrm{0}\tag{8-98}\]
The vertical equilibrium of forces:
\[\ \sum \mathrm{F}_{\mathrm{v}}=-\mathrm{K}_{\mathrm{1}} \cdot \cos (\boldsymbol{\beta}+\boldsymbol{\varphi})+\mathrm{C} \cdot \sin (\boldsymbol{\beta})-\mathrm{K}_{\mathrm{2}} \cdot \cos (\boldsymbol{\alpha}+\boldsymbol{\delta})=\mathrm{0}\tag{8-99}\]
The force K1 on the shear plane is now:
\[\ \mathrm{K}_{1}=\frac{-\mathrm{C} \cdot \cos (\alpha+\beta+\delta)}{\sin (\alpha+\beta+\delta+\varphi)}\tag{8-100}\]
The force K2 on the blade is now:
\[\ \mathrm{K_{2}=\frac{C \cdot \cos (\varphi)}{\sin (\alpha+\beta+\delta+\varphi)}}\tag{8-101}\]
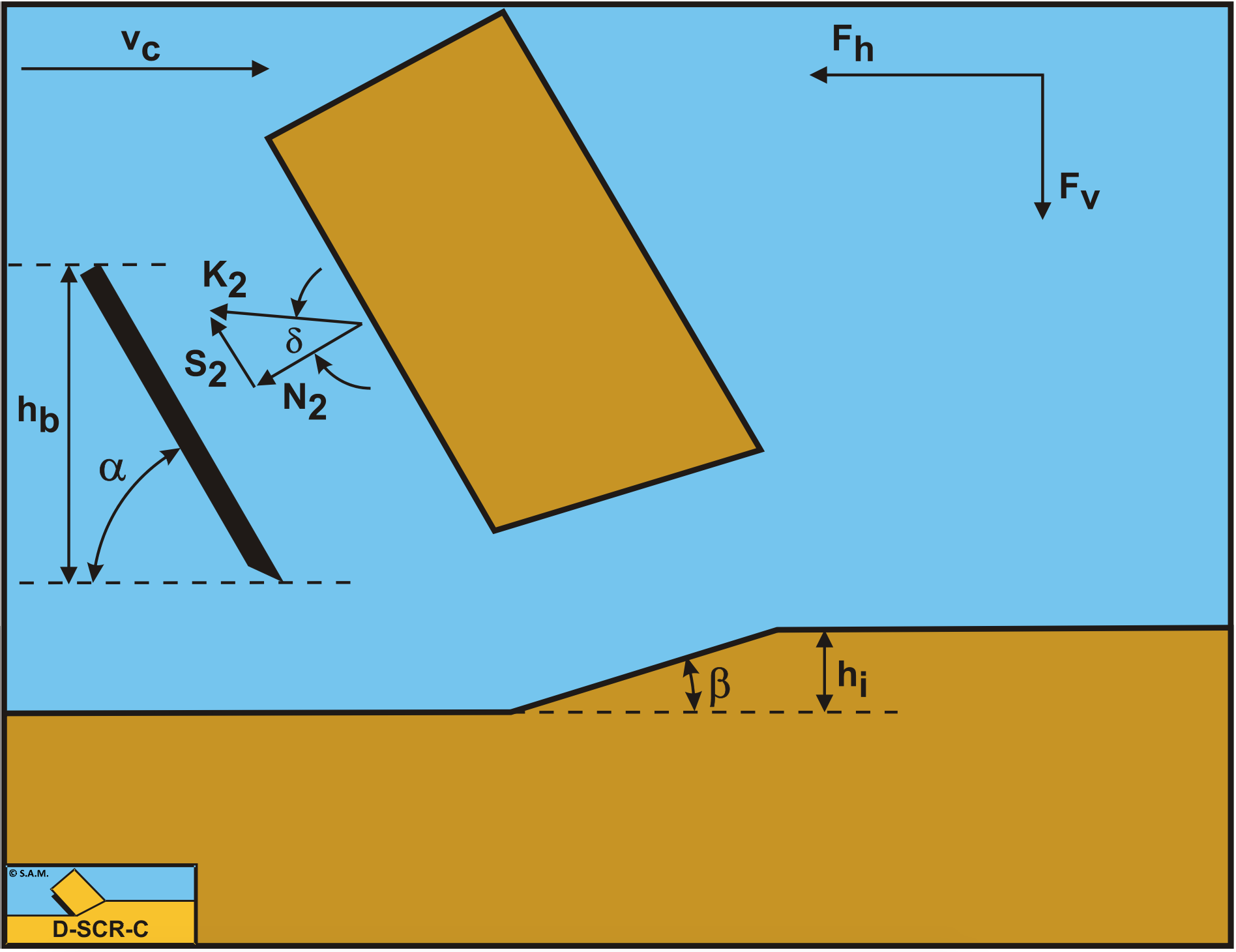
The force C due to the cohesive shear strength c is equal to:
\[\ \mathrm{C}=\frac{\lambda_{\mathrm{s}} \cdot \mathrm{c} \cdot \mathrm{h}_{\mathrm{i}} \cdot \mathrm{w}}{\sin (\beta)}\tag{8-102}\]
The factor λs in equation (8-102) is the velocity strengthening factor, which causes an increase of the cohesive shear strength. In clay (Miedema (1992) and (2010)) this factor has a value of about 2 under normal cutting conditions. In rock the strengthening effect is not reported, so a value of 1 should be used. From equation (8-101) the forces on the blade can be derived. On the blade a force component in the direction of cutting velocity Fh and a force perpendicular to this direction Fv can be distinguished.
\[\ \mathrm{F_{h}=K_{2} \cdot \sin (\alpha+\delta)}\tag{8-103}\]
\[\ \mathrm{F}_{v}=\mathrm{K}_{\mathrm{2}} \cdot \cos (\alpha+\delta)\tag{8-104}\]
Substituting equations (8-102) and (8-101) gives the following equations for the horizontal Fh and vertical Fv cutting forces. It should be remarked that the strengthening factor λs in rock is usually 1.
\[\ \mathrm{F_{h}=\frac{\lambda_{s} \cdot c \cdot h_{i} \cdot w \cdot \cos (\varphi) \cdot \sin (\alpha+\delta)}{\sin (\beta) \cdot \sin (\alpha+\beta+\delta+\varphi)}}\tag{8-105}\]
\[\ \mathrm{F}_{v}=\frac{\lambda_{\mathrm{s}} \cdot \mathrm{c} \cdot \mathrm{h}_{\mathrm{i}} \cdot \mathrm{w} \cdot \cos (\varphi) \cdot \cos (\alpha+\delta)}{\sin (\beta) \cdot \sin (\alpha+\beta+\delta+\varphi)}\tag{8-106}\]


