8.8: Specific Energy
- Page ID
- 34844
For the cases as described above, cutting with a straight blade with the direction of the cutting velocity vc perpendicular to the blade (edge of the blade), the specific cutting energy Esp is:
\[\ \mathrm{E}_{\mathrm{sp}}=\frac{\mathrm{F}_{\mathrm{h}} \cdot \mathrm{v}_{\mathrm{c}}}{\mathrm{h}_{\mathrm{i}} \cdot \mathrm{w} \cdot \mathrm{v}_{\mathrm{c}}}=\frac{\mathrm{F}_{\mathrm{h}}}{\mathrm{h}_{\mathrm{i}} \cdot \mathrm{w}}\tag{8-137}\]
The specific energy of the Flow Type or Crushed Type of cutting mechanism can be written as:
\[\ \mathrm{E}_{\mathrm{s p}}=\lambda_{\mathrm{H F}} \cdot \mathrm{c}\tag{8-138}\]
The specific energy of the Tear Type or Chip Type of cutting mechanism can be written as:
\[\ \mathrm{E}_{\mathrm{s p}}=\lambda_{\mathrm{H T}} \cdot \sigma_{\mathrm{T}}\tag{8-139}\]
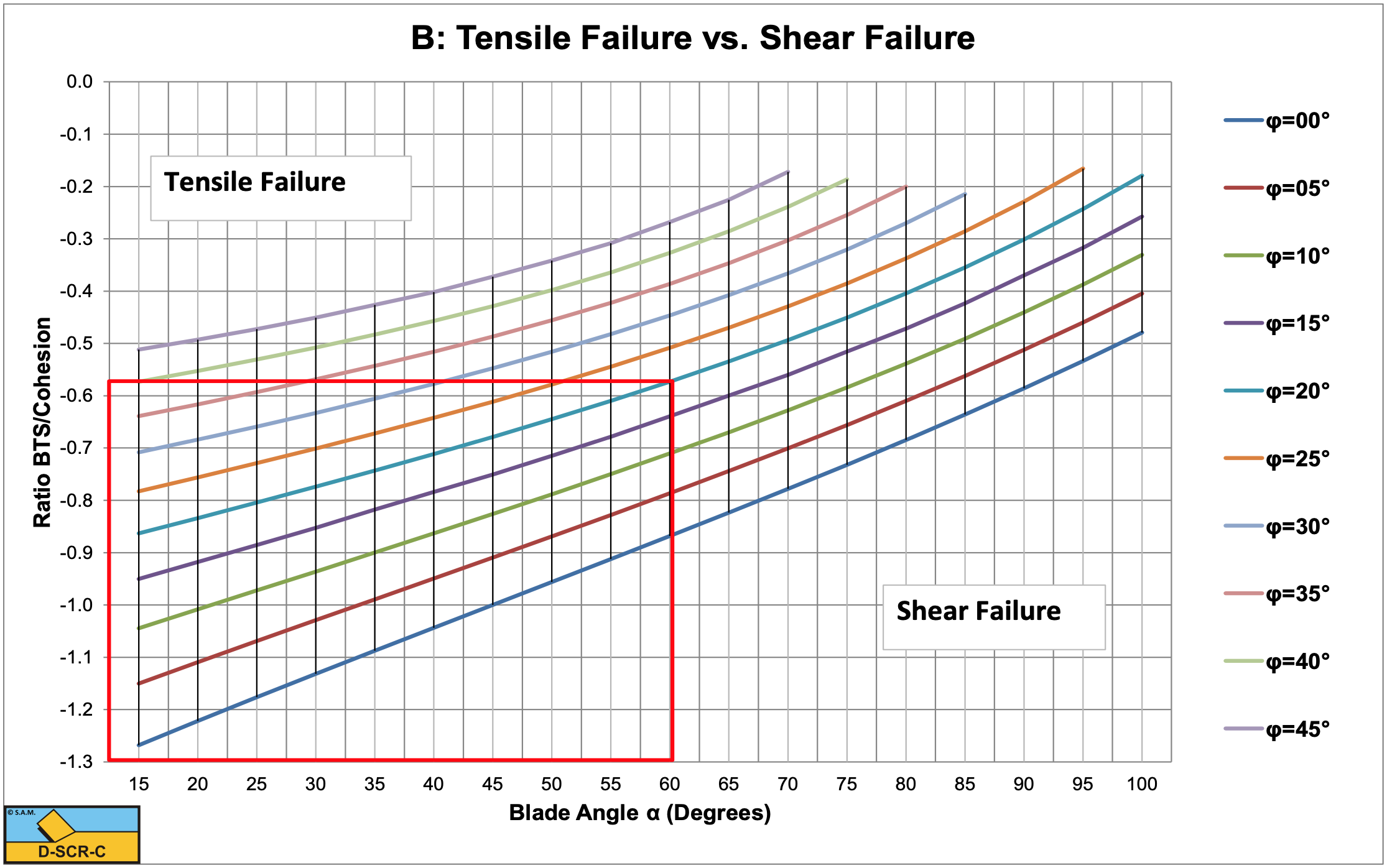
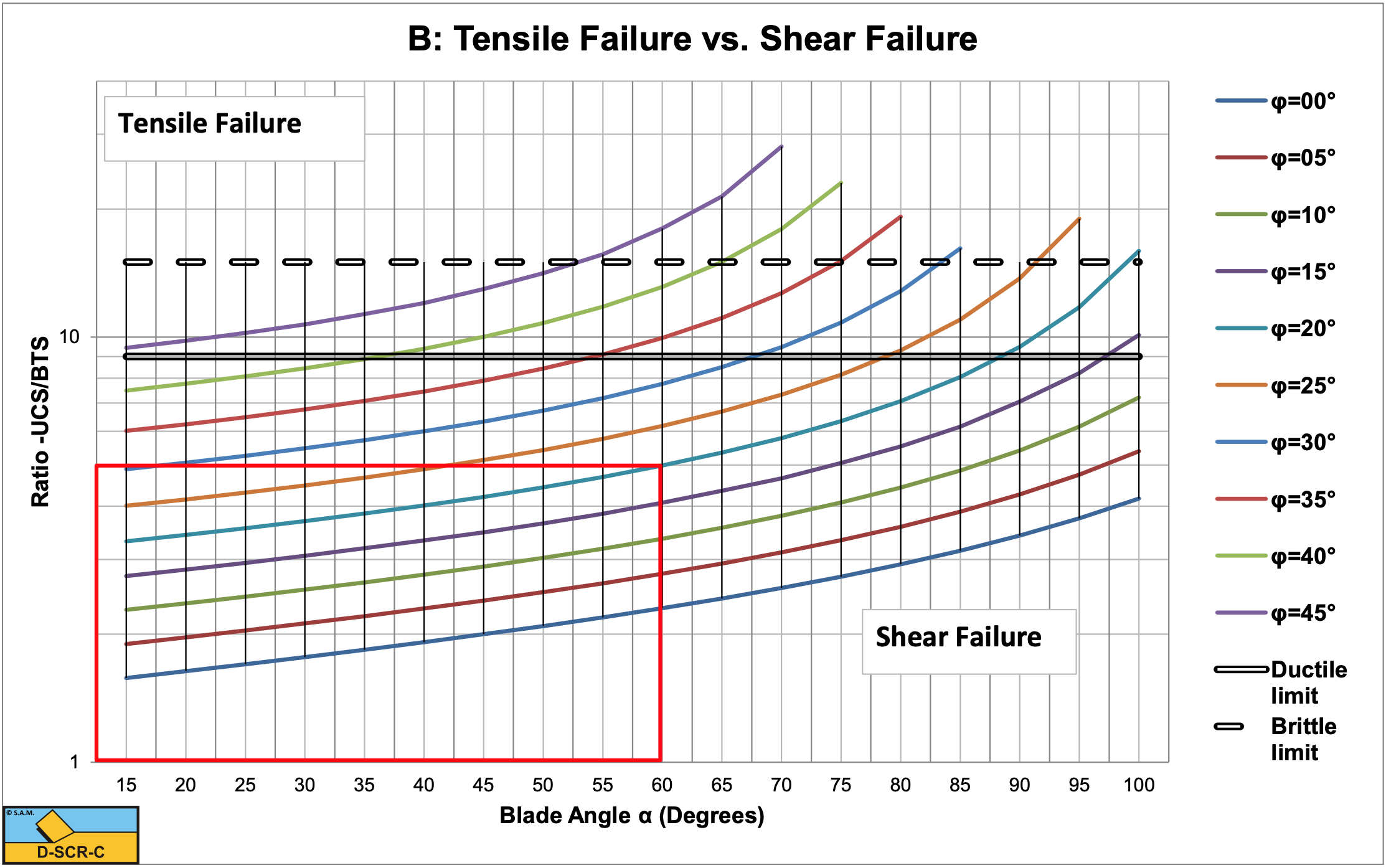
Since the specific energy equations are based on the maximum horizontal cutting forces, where the cutting process is most probably either brittle shear or brittle tensile, the average cutting forces will be smaller. How much smaller depends on the type of rock, but literature mentions reductions by 30% to 70%. Since the specific energy is based on the average cutting forces, the values found with the above equations should be multiplied by a factor of 0.3- 0.7.