11.1: Introduction

Last updated
Save as PDF

Page ID: 29352

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

The cutting theories until now works well for small blade angles, however when the blade angle and the other angles involved increase, a problem with the model may occur. The basic equations contain a denominator with the sine of the sum of the blade angle, the shear angle, the internal friction angle and the external friction angle. So if the sum of these angles equals 180 degrees, the denominator is zero, meaning a division by zero giving infinity. Even worse, if the sum of these angles is greater than 180 degrees the sine gives a negative result, meaning the cutting forces become negative. But already if the sum of these angles approach 180 degrees the sine becomes very small and since it is in the denominator, the cutting forces would become very high. Now nature will normally choose the road of least resistance, nature will try to find another mechanism for the cutting process and this mechanism might be the occurrence of a wedge in front of the blade. This wedge will form a pseudo cutting blade A-C with a blade angle much smaller than the angle of the real blade. The probability of the occurrence of a wedge is large for sand and rock since all 4 angles mentioned play a role there. For clay the probability is much smaller, since in clay cutting normally the internal and external friction angles do not play a role.

Now nature may choose another mechanism which will result in even smaller cutting forces, like the model of Hettiaratchi & Reece (1975), but their model is more complicated. The philosophy here is that if a mechanism can be found resulting in smaller cutting forces than the model used for small blade angles, this model will give a better prediction than the model for small blade angles. The wedge mechanism is such a mechanism, with the advantage that it is relatively simple to use and the cutting forces predicted with this model match the cutting forces from the experiments of Hatamura & Chijiiwa (1977B) pretty close. So from a pragmatic point of view this mechanism will be discussed for large blade angles.

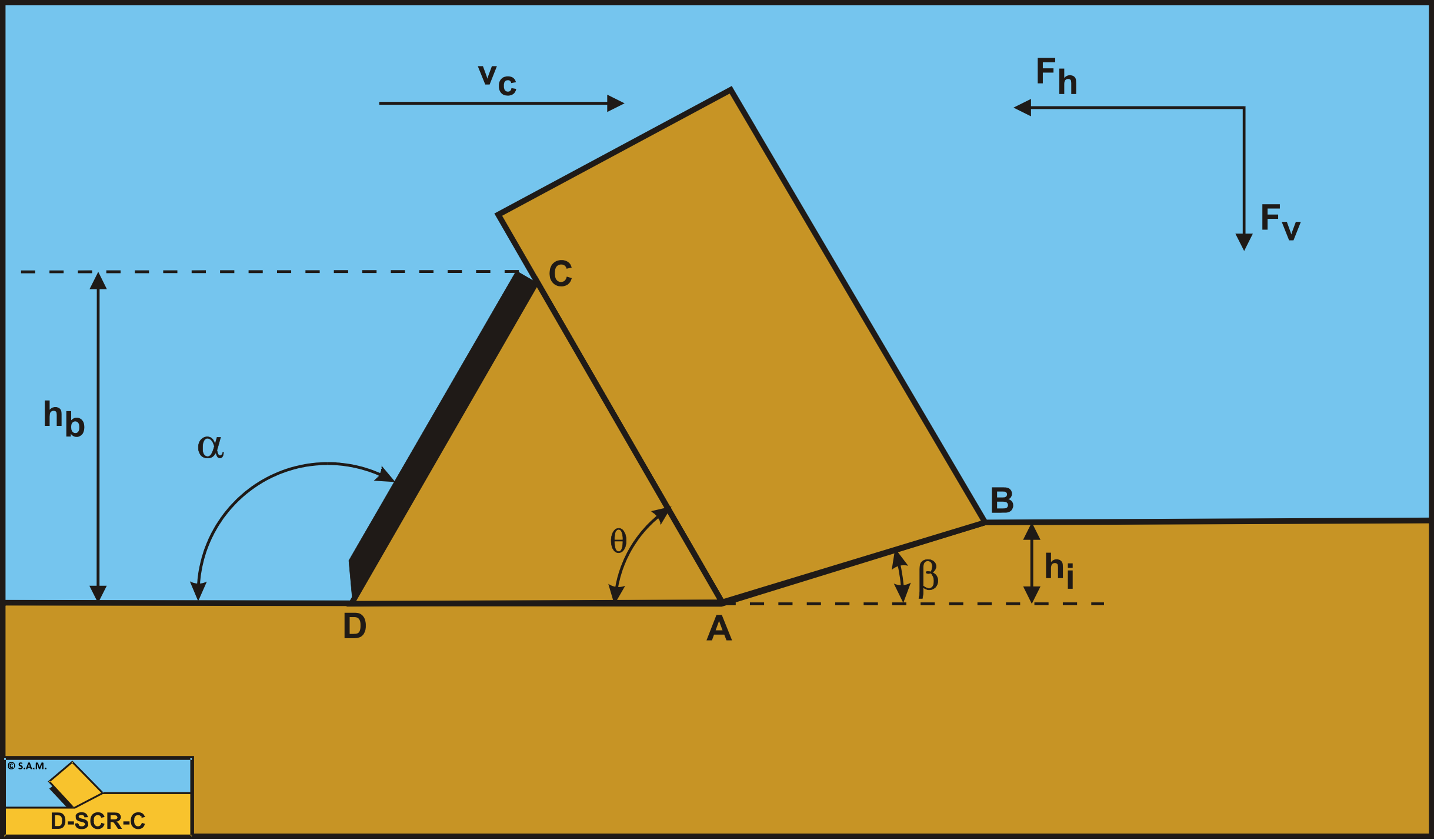
Screen Shot 2020-08-24 at 5.00.57 PM.png — Figure 11-1: Definitions.

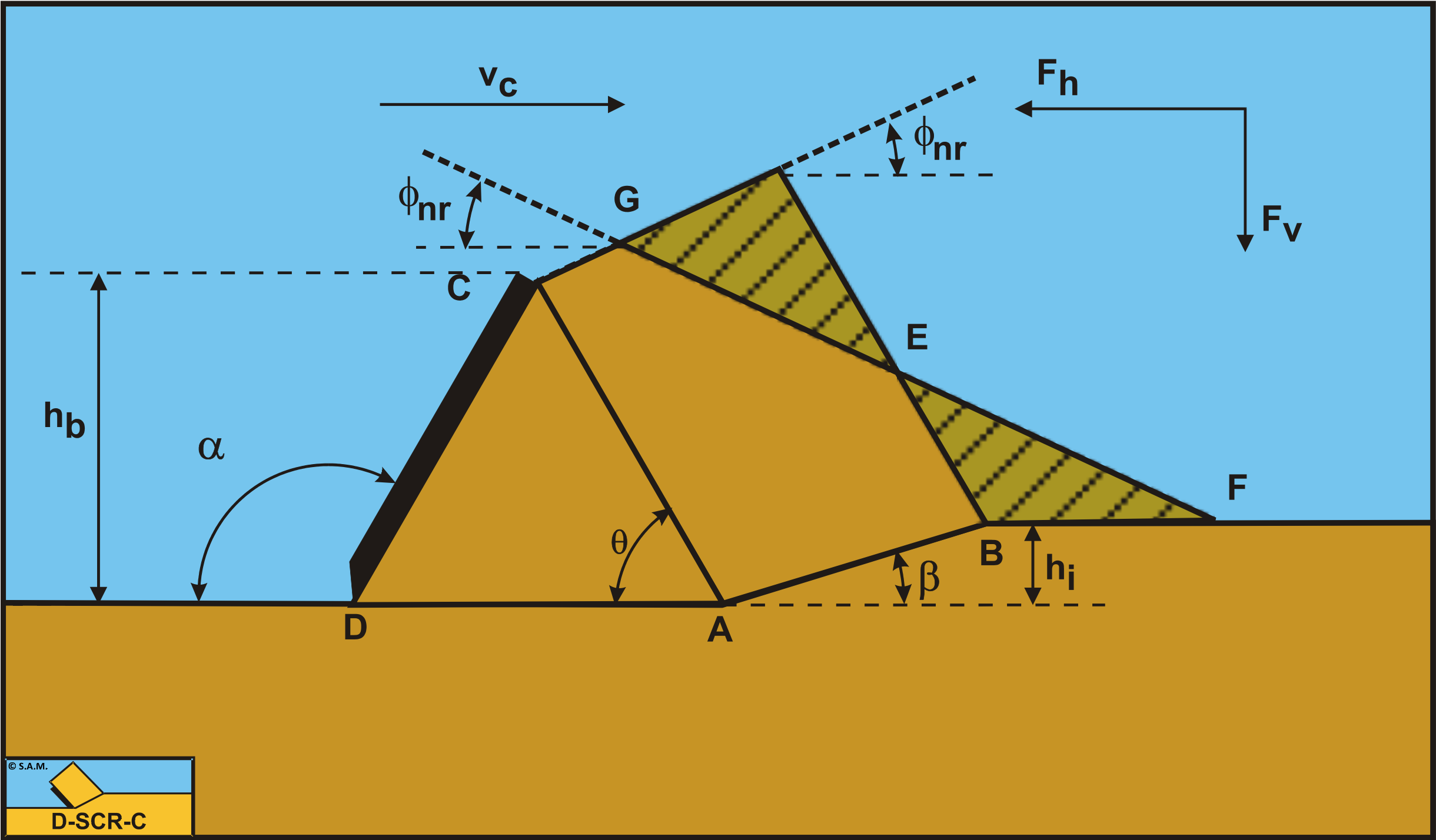
Screen Shot 2020-08-24 at 5.02.01 PM.png — Figure 11-2: Alternative geometry of the layer cut.

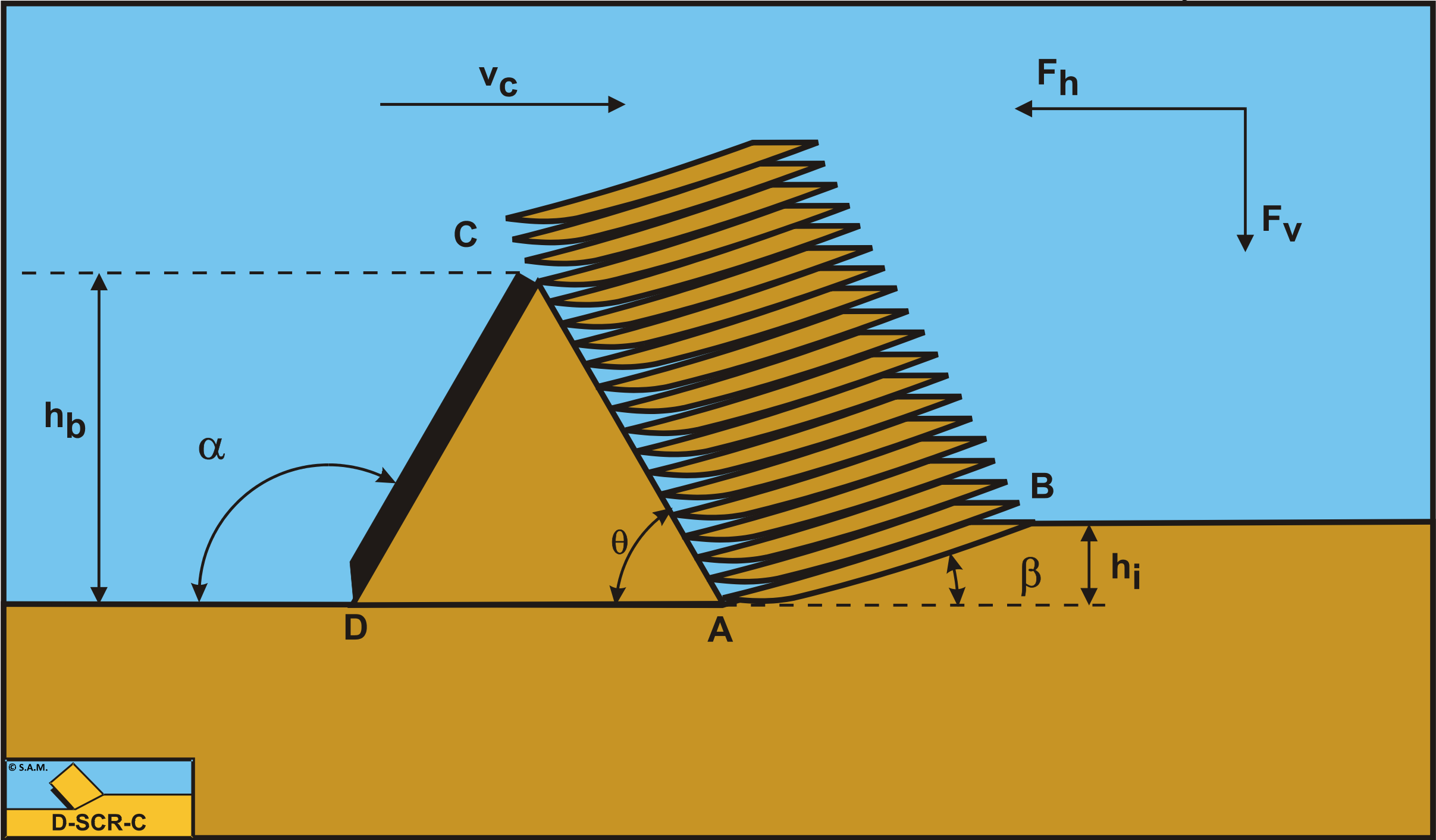
Screen Shot 2020-08-24 at 5.03.11 PM.png — Figure 11-3: The cutting mechanism.

Definitions:

A: The wedge tip.
B: End of the shear plane.
C: The blade top.
D: The blade tip.
A-B: The shear plane.
A-C: The wedge surface.
A-D: The wedge bottom.
D-C: The blade surface.
h_b: The height of the blade.
h_i: The thickness of the layer cut.
v_c: The cutting velocity.
α: The blade angle.
β: The shear angle.
F_h: The horizontal force, the arrow gives the positive direction.
F_v: The vertical force, the arrow gives the positive direction.

For the weight of the layer cut G₁, see chapter 5: Dry Sand Cutting.

The weight of the wedge G₂ is given by:

\[\ \mathrm{G}_{2}=\rho_{s} \cdot \mathrm{g} \cdot \frac{\mathrm{h}_{\mathrm{b}}^{2}}{2} \cdot\left(\frac{1}{\tan (\theta)}-\frac{1}{\tan (\alpha)}\right) \cdot \mathrm{w}\tag{11-1}\]