11.4: Results of some Calculations

Last updated
Save as PDF

Page ID: 29355

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Since the wedge model depends on many parameters, some example calculations are carried out with the parameters as used by Hatamura & Chijiiwa (1977B). The calculations are carried out with a blade height h_b=0.2 m, a blade width w=0.33 m, an angle of internal friction φ=38°, an angle of internal friction δ=2/3·φ, an angle of internal friction on the pseudo blade of λ=32°, a dry density of ρ_s=1.59 ton/m³ and a cutting velocity of v_c=0.05 m/sec. The difference with the Hatamura & Chijiiwa (1977B) experiments is that here the blade height is constant, while in their experiments the blade length was constant. Further layer thicknesses of h_i=0.066 m, 0.10 m and 0.20 m are used in the calculations. Based on these and many more calculations an empirical equation has been found for the wedge angle θ.

\[\ \mathrm{\theta=(90-\varphi) \cdot\left(0.73+0.0788 \cdot \frac{h_{\mathrm{b}}}{h_{\mathrm{i}}}\right)}\tag{11-28}\]

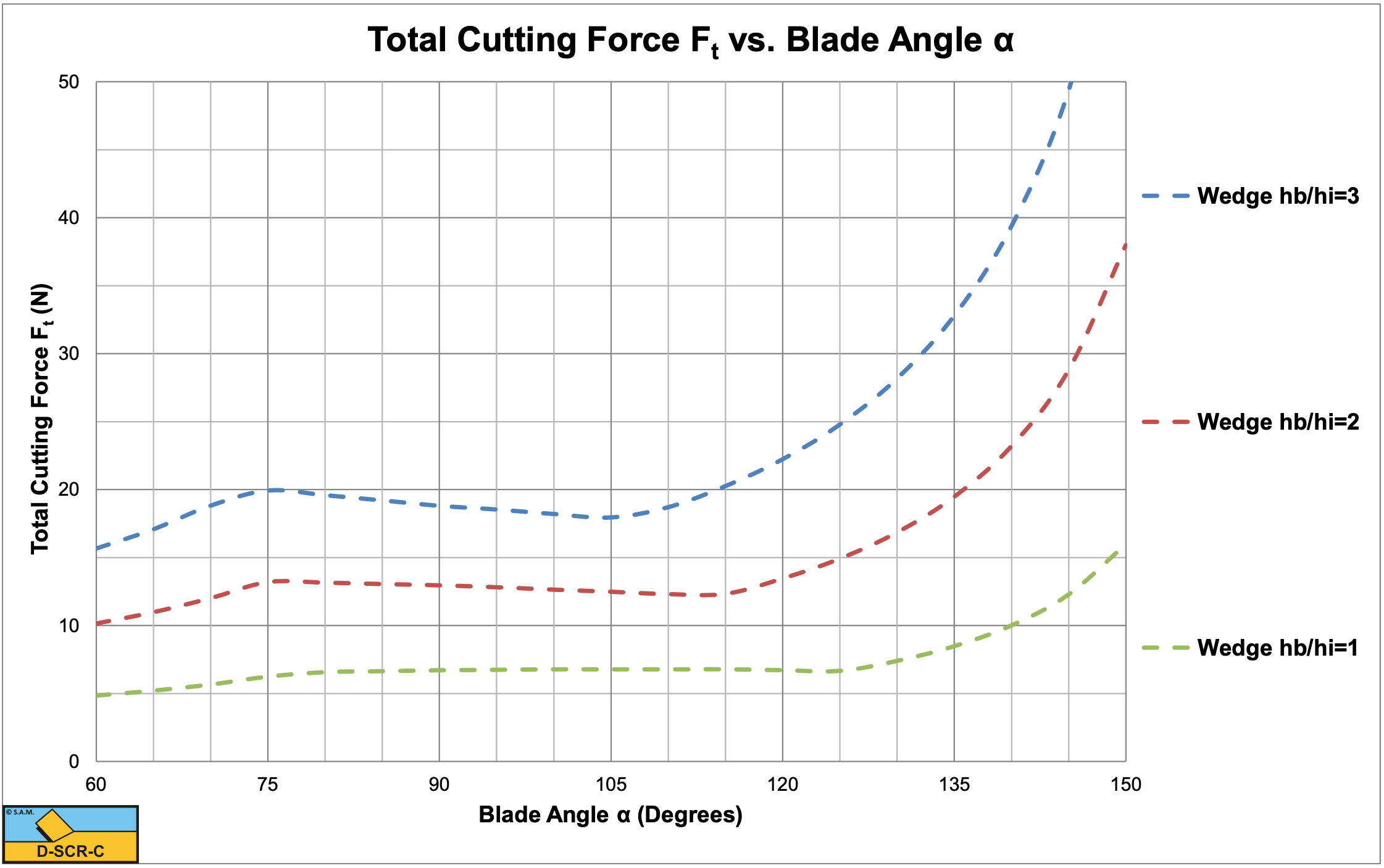
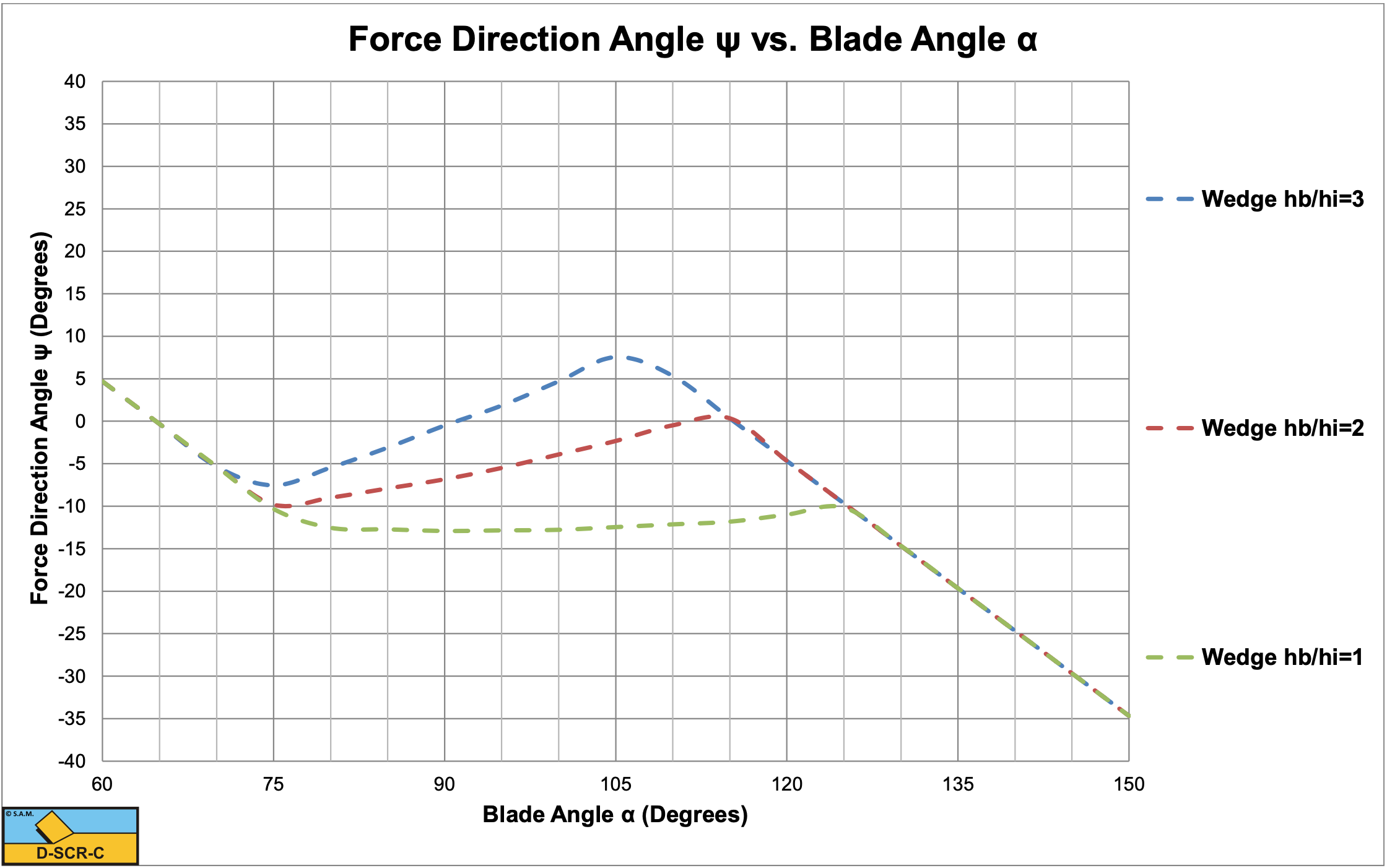
Figure 11-8, Figure 11-9 and Figure 11-10 show the shear angle, the mobilized external friction angle, the wedge angle, the total cutting force and the direction of the total cutting force.

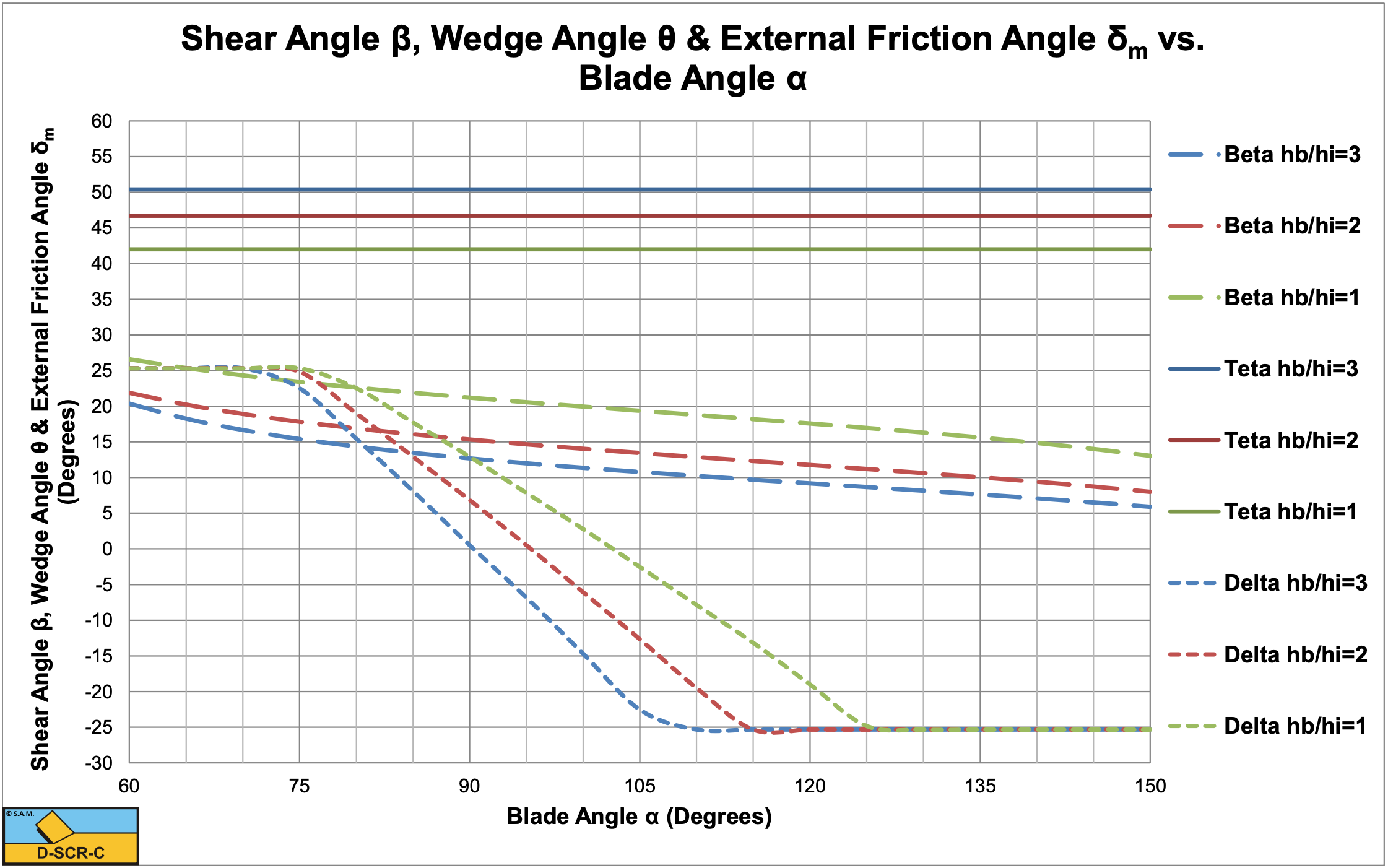
Screen Shot 2020-08-24 at 6.25.26 PM.png — Figure 11-8: The shear angle, wedge angle and mobilized external friction angle calculated with wedge.

In the region where the mobilized external friction angle changes from plus the maximum to minus the maximum value, an equilibrium of moments exists. In the case considered this means that a wedge may exist in this region. When the mobilized external friction angle equals minus the maximum value there is no equilibrium of moments. In this region the total cutting force increases rapidly with an increasing blade angle in the calculations, but most probably another mechanism than the wedge mechanism will occur, so the values of the cutting forces in that region are not reliable. In the region of the mobilized external friction angle between plus the maximum to minus the maximum value the total cutting force is almost constant.

Screen Shot 2020-08-24 at 6.26.50 PM.png — Figure 11-9: The total cutting force.

Screen Shot 2020-08-24 at 6.27.32 PM.png — Figure 11-10: The direction of the total cutting force.