12.1: Introduction
- Page ID
- 29359
In the last decennia extensive research has been carried out into the cutting of water saturated sand. In the cutting of water-saturated sand, the phenomenon of dilatation plays an important role. In fact the effects of gravity, inertia, cohesion and adhesion can be neglected at cutting speeds in the range of 0.5 – 10 m/s. In the cutting equations, as published by Miedema (1987 September), there is a division by the sine of the sum of the blade angle, the shear angle, the angle of internal friction and the soil/interface friction angle. When the sum of these angle approaches 180o, a division by zero is the result, resulting in infinite cutting forces. This may occur for example for α=80o, α=30o, α=40o and α=30o. When this sum is greater than 180 degrees, the cutting forces become negative. It is obvious that this cannot be the case in reality and that nature will look for another cutting mechanism.
Hettiaratchi and Reece (1975) found a mechanism, which they called boundary wedges for dry soil. At large cutting angles a triangular wedge will exist in front of the blade, not moving relative to the blade. This wedge acts as a blade with a smaller blade angle. In fact, this reduces the sum of the 4 angles mentioned before to a value much smaller than 180o. The existence of a dead zone (wedge) in front of the blade when cutting at large cutting angles will affect the value and distribution of vacuum water pressure on the interface. He et al. (1998) proved experimentally that also in water saturated sand at large cutting angles a wedge will occur. A series of tests with rake angles 90, 105 and 120 degrees under fully saturated and densely compacted sand condition was performed by He et al. (1998) at the Dredging Technology Laboratory of Delft University of Technology. The experimental results showed that the failure pattern with large rake angles is quite different from that with small rake angles. For large rake angles a dead zone is formed in front of the blade, but not for small rake angles. In the tests he carried out, both a video camera and film camera were used to capture the failure pattern. The video camera was fixed on the frame which is mounted on the main carriage, translates with the same velocity as the testing cutting blade. Shown in the static slide of the video record, as in Figure 12-1, the boundary wedges exist during the cutting test. The assumption of an alternative failure mechanism is based on a small quantity of picture material, see Figure 12-1. It is described as a static wedge in front of the blade, which serves as a new virtual blade over which the sand flows away.

Although the number of experiments published is limited, the research is valuable as a starting point to predict the shape of the wedge. At small cutting angles the cutting forces are determined by the horizontal and vertical force equilibrium equations of the sand cut in front of the blade. These equations contain 3 unknowns, so a third equation/condition had to be found. The principle of minimum energy is used as a third condition to solve the 3 unknowns. This has proved to give very satisfactory results finding the shear angle and the horizontal and vertical cutting forces at small cutting angles. At large cutting angles, a 4th unknown exists, the wedge angle or virtual blade angle. This means that a 4th equation/condition must be found in order to determine the wedge angle. There are 3 possible conditions that can be used: The principle of minimum energy, the circle of Mohr, The equilibrium of moments of the wedge. In fact, there is also a 5th unknown, the mobilized friction on the blade. New research carried out in the Dredging Engineering Laboratory shows that a wedge exists, but not always a static wedge. The sand inside the wedge is still moving, but with a much lower velocity then the sand outside the wedge. This results in fully mobilized friction on the blade. The bottom boundary of the wedge, which is horizontal for a static wedge, may have a small angle with respect to the horizontal in the new case considered.
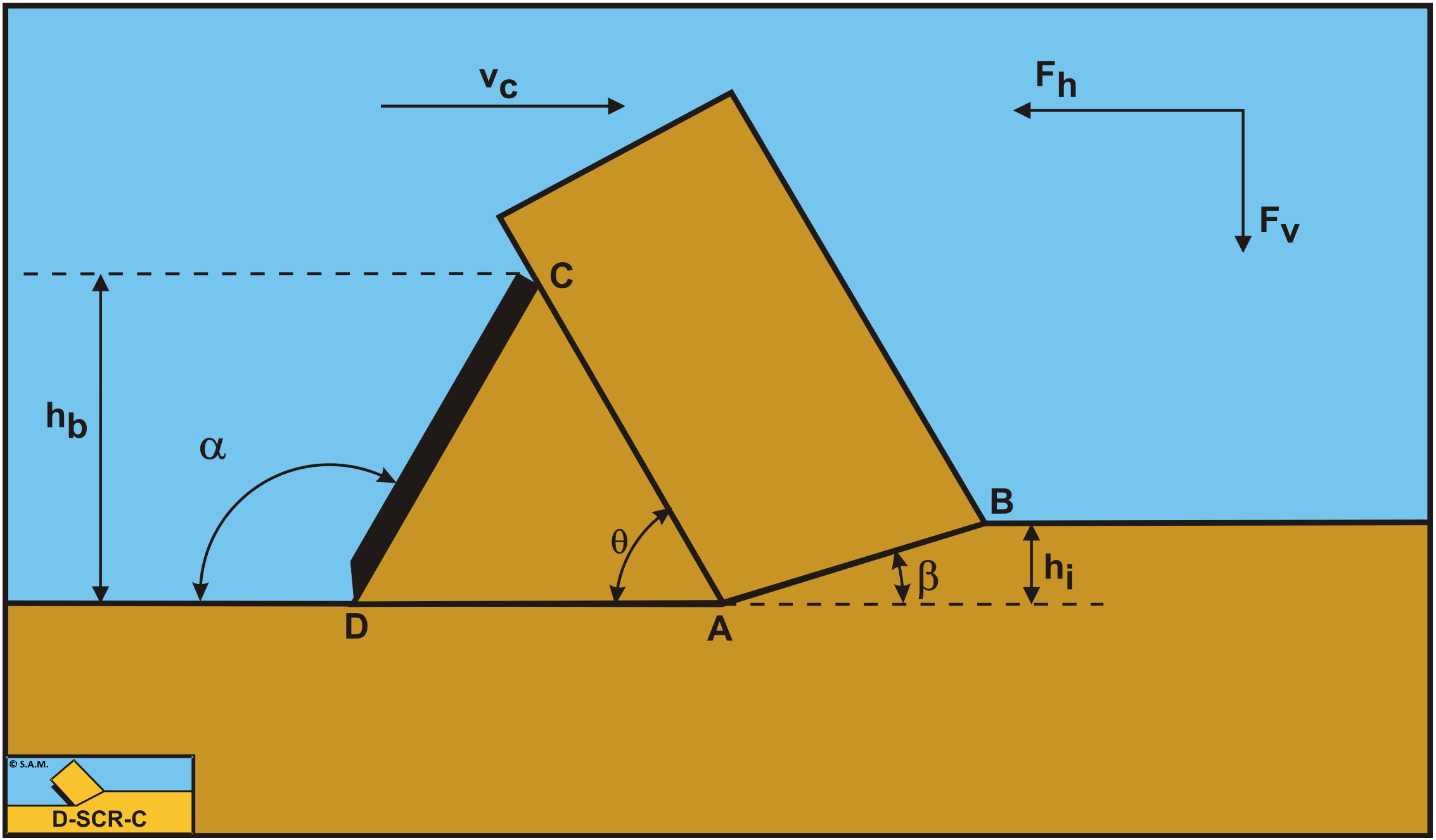
Definitions:
-
A: The wedge tip.
-
B: End of the shear plane.
-
C: The blade top.
-
D: The blade tip.
-
A-B: The shear plane.
-
A-C: The wedge surface.
-
A-D: The wedge bottom.
-
D-C: The blade surface.
-
hb: The height of the blade.
-
hi: The thickness of the layer cut.
-
vc: The cutting velocity.
-
α: The blade angle.
-
β: The shear angle.
-
Fh: The horizontal force, the arrow gives the positive direction.
-
Fv: The vertical force, the arrow gives the positive direction.
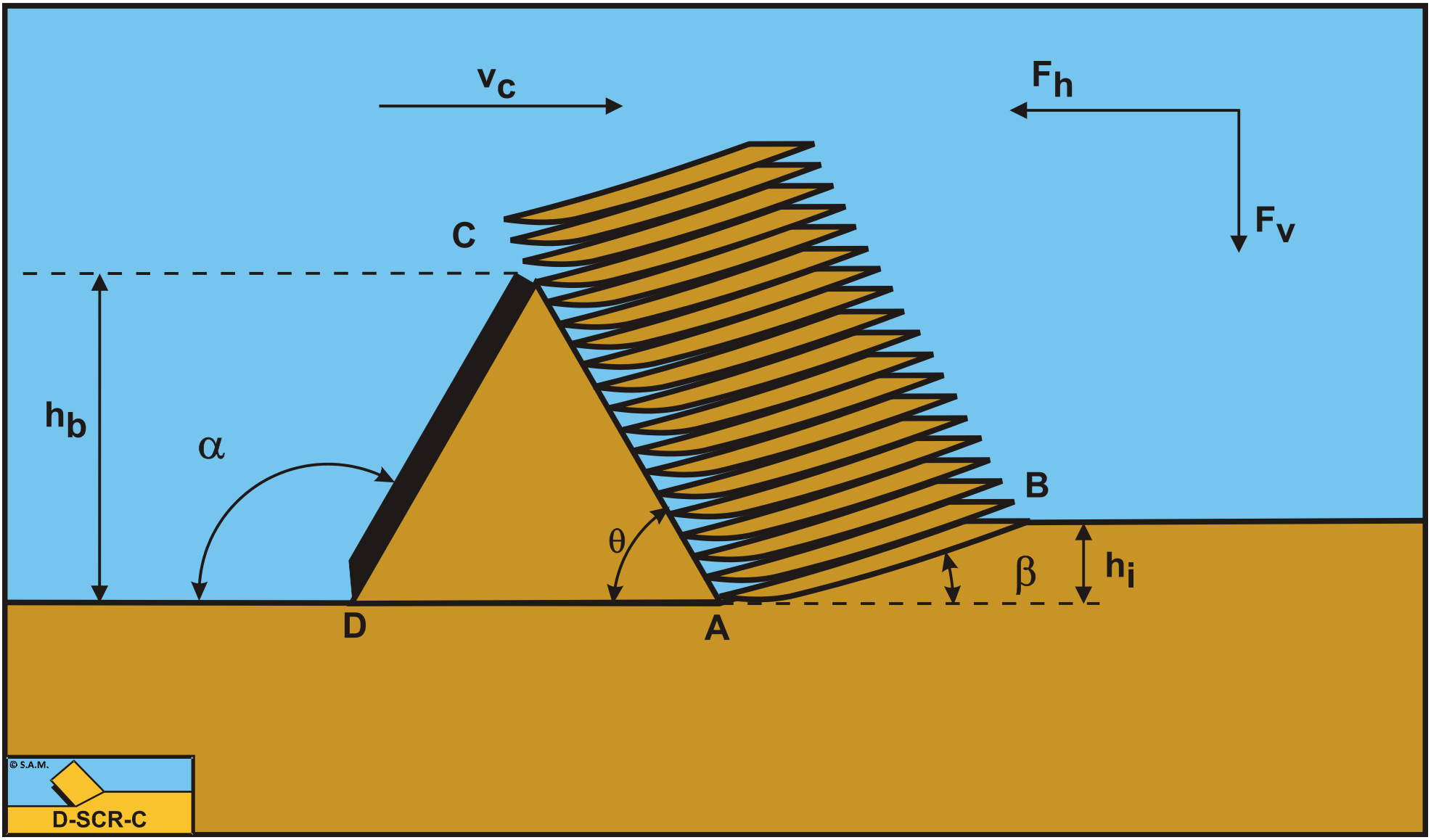
Figure 12-2 shows the definitions of the cutting process with a static wedge. A-B is the shear plane where dilatation occurs. A-C is the front of the static wedge and forms a pseudo cutting blade. A-C-D is the static wedge, where C- D is the blade, A-D the bottom of the wedge and A-C the pseudo blade or the front of the wedge.
The sand wedge theory is based on publications of Hettiaratchi and Reece (1975), Miedema (1987 September), He et al. (1998), Yi (2000), Miedema et al. (2001), Yi et al. (2001), Ma (2001), Miedema et al. (2002A), Miedema et al. (2002B), Yi et al. (2002), Miedema (2003), Miedema et al. (2003), Miedema (2004), Miedema et al. (2004), He et al. (2005), Ma et al. (2006A), Ma et al. (2006B), Miedema (2005), Miedema (2006A), Miedema (2006B).


