Skip to main content
Engineering LibreTexts

12.2: The Equilibrium of Forces

  1. Last updated
  2. Save as PDF
  • Page ID
    29360

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

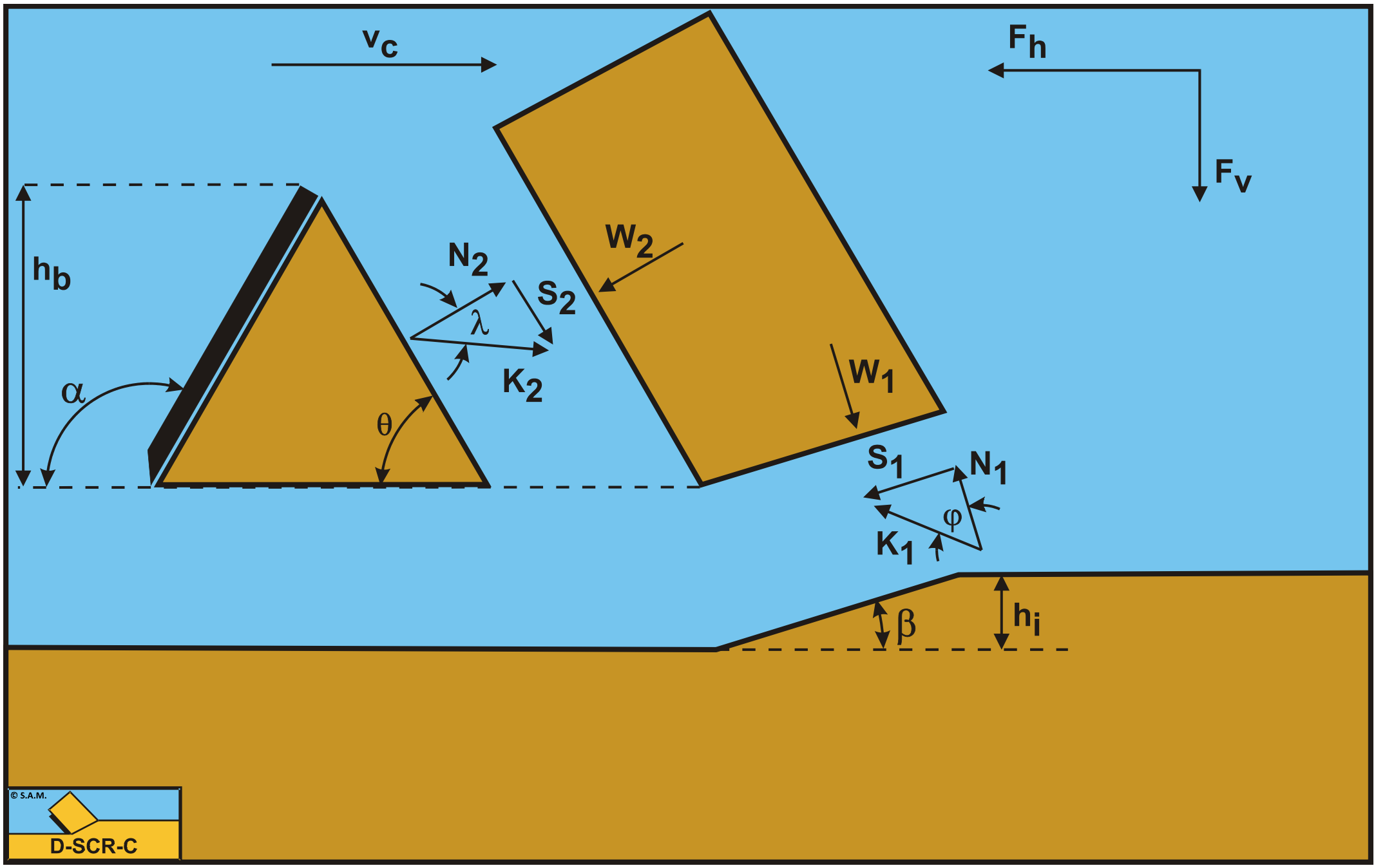
    Figure 12-4, Figure 12-5 and Figure 12-6 show the forces occurring at the layer cut, the wedge and the blade, while

    Figure 12-18 shows the moments occurring on the wedge. The forces are:

    The forces acting on the layer A-B are:

    1. A normal force acting on the shear surface N1, resulting from the effective grain stresses.

    2. A shear force S1 as a result of internal friction N1·tan(φ).

    3. A force W1 as a result of water under pressure in the shear zone.

    4. A shear force S2 as a result of the soil/soil friction N2·tan(λ) between the layer cut and the wedge pseudo blade. The friction angle λ does not have to be equal to the internal friction angle φ in the shear plane, since the soil has already been deformed.

    5. A force W2 as a result of water under pressure on the wedge.

    The forces acting on the wedge front or pseudo blade A-C when cutting soil, can be distinguished as:

    1. A force normal to the blade N2, resulting from the effective grain stresses.

    2. A shear force S2 as a result of the soil/soil friction N2·tan(λ) between the layer cut and the wedge pseudo blade. The friction angle λ does not have to be equal to the internal friction angle φ in the shear plane, since the soil has already been deformed.

    3. A force W2 as a result of water under pressure on the pseudo blade A-C.

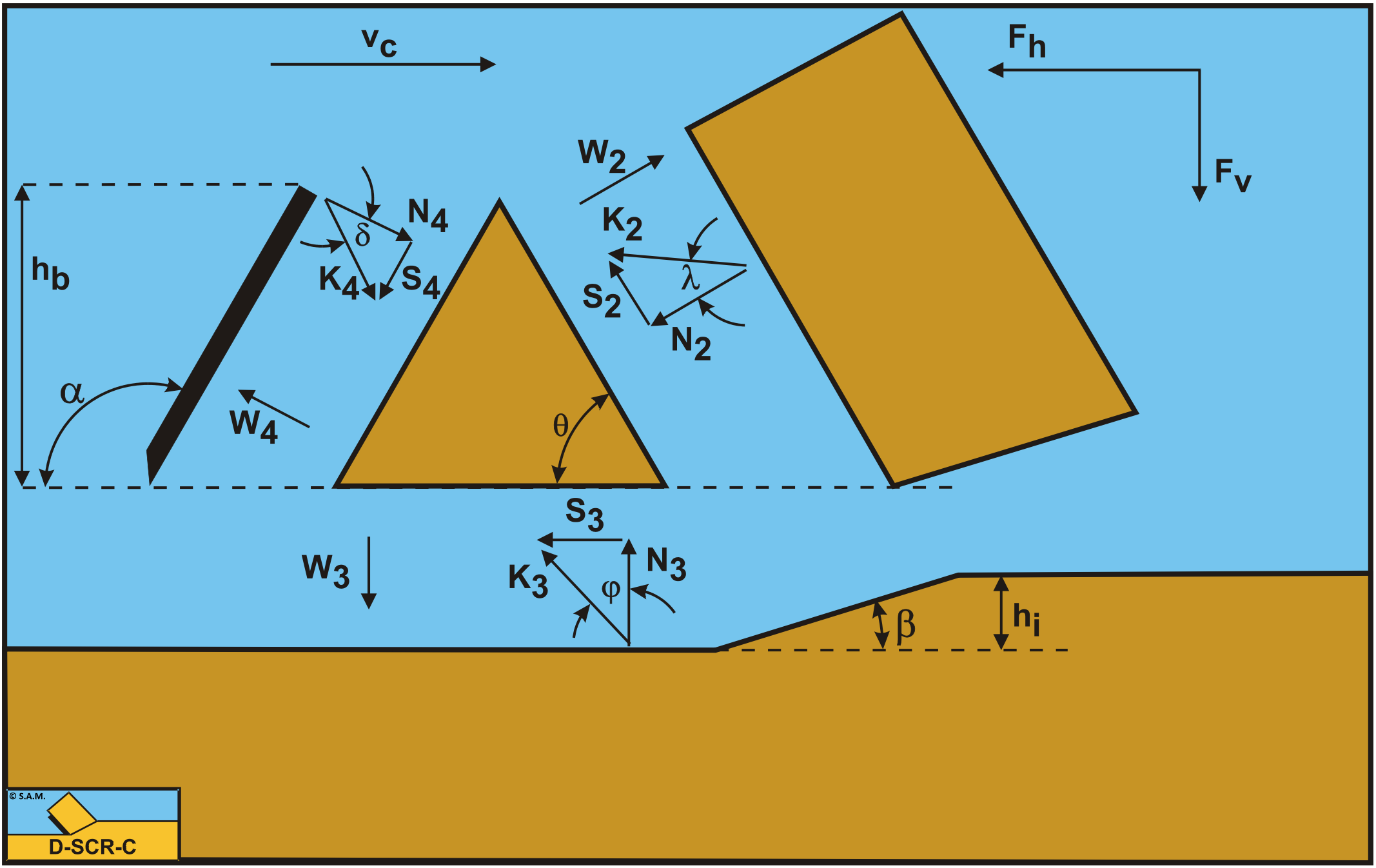
    The forces acting on the wedge bottom A-D when cutting soil, can be distinguished as:

    1. A force N3, resulting from the effective grain stresses, between the wedge bottom and the undisturbed soil.

    2. A shear force S3 as a result of the soil/soil friction N3·tan(φ)  between the wedge bottom and the undisturbed soil.

    3. A force W3 as a result of water under pressure on the wedge bottom A-D.

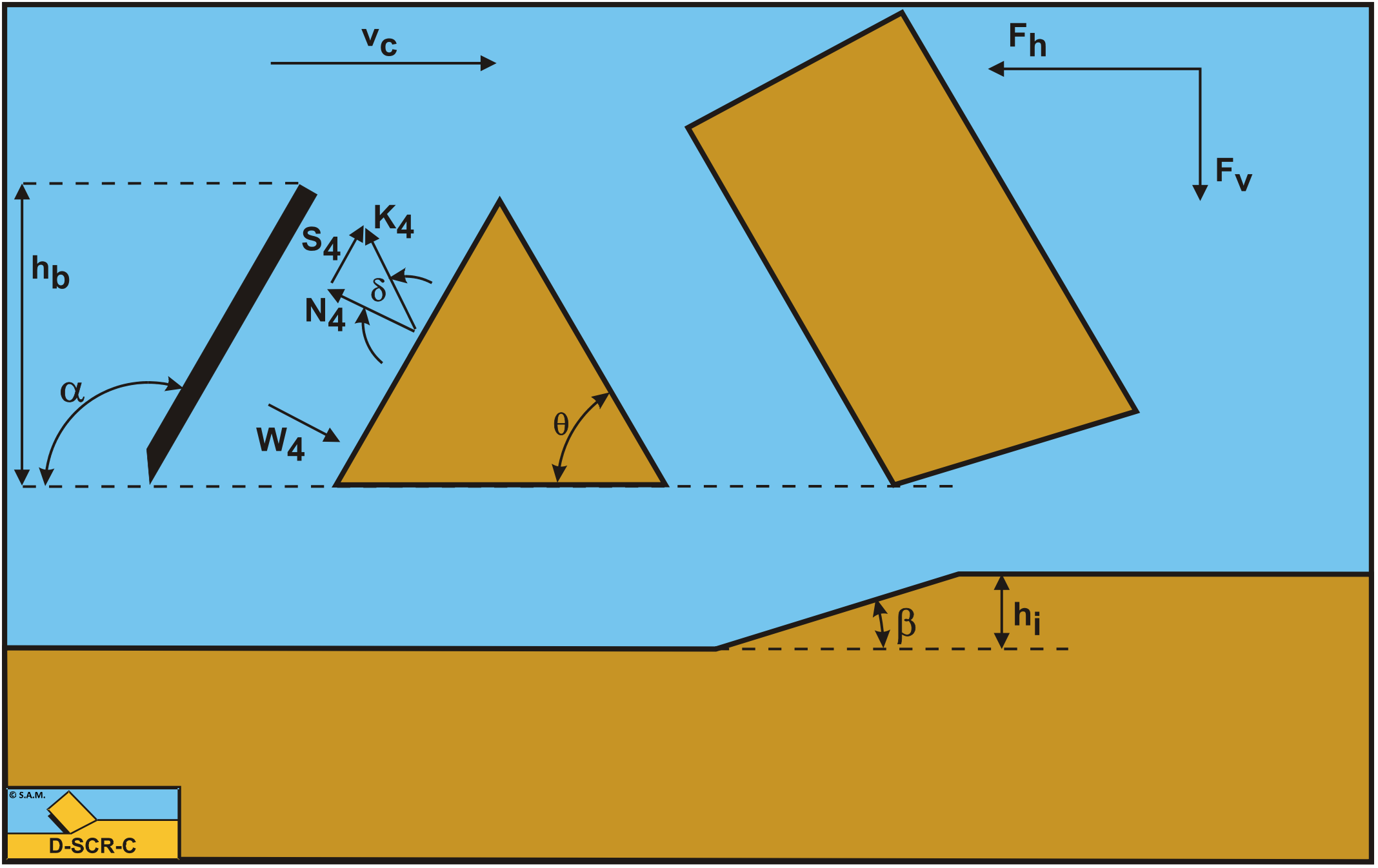
    The forces acting on a straight blade C-D when cutting soil, can be distinguished as:

    1. A force normal to the blade N4, resulting from the effective grain stresses.

    2. A shear force S4 as a result of the soil/steel friction N4·tan(δ) between the wedge and the blade.

    3. A force W4 as a result of water under pressure on the blade.

    To determine the cutting forces on the blade, first the cutting forces on the pseudo blade have to be determined by taking the horizontal and vertical equilibrium of forces on the layer cut B-A-C. The shear angle β is determined by minimizing the cutting energy.

    The horizontal equilibrium of forces:

    \[\ \sum \mathrm{F}_{\mathrm{h}}=\mathrm{K}_{\mathrm{1}} \cdot \sin (\boldsymbol{\beta}+\boldsymbol{\varphi})-\mathrm{W}_{\mathrm{1}} \cdot \sin (\boldsymbol{\beta})+\mathrm{W}_{\mathrm{2}} \cdot \sin (\boldsymbol{\theta})-\mathrm{K}_{\mathrm{2}} \cdot \mathrm{\operatorname { sin } ( \boldsymbol { \theta } + \lambda )}=\mathrm{0}\tag{12-1}\]

    The vertical equilibrium of forces:

    \[\ \sum \mathrm{F}_{\mathrm{v}}=-\mathrm{K}_{\mathrm{1}} \cdot \cos (\boldsymbol{\beta}+\boldsymbol{\varphi})+\mathrm{W}_{\mathrm{1}} \cdot \cos (\boldsymbol{\beta})+\mathrm{W}_{\mathrm{2}} \cdot \mathrm{\operatorname { cos } ( \boldsymbol { \theta } ) - \mathrm { K } _ { \mathrm { 2 } }} \cdot \cos (\boldsymbol{\theta}+\lambda)=\mathrm{0}\tag{12-2}\]

    The force K1 on the shear plane is now:

    \[\ \mathrm{K}_{1}=\frac{\mathrm{W}_{2} \cdot \sin (\lambda)+\mathrm{W}_{1} \cdot \sin (\theta+\beta+\lambda)}{\sin (\theta+\beta+\lambda+\varphi)}\tag{12-3}\]

    The force K2 on the pseudo blade is now:

    \[\ \mathrm{K}_{2}=\frac{\mathrm{W}_{2} \cdot \sin (\theta+\beta+\varphi)+\mathrm{W}_{1} \cdot \sin (\varphi)}{\sin (\theta+\beta+\lambda+\varphi)}\tag{12-4}\]

    Screen Shot 2020-08-24 at 7.39.00 PM.png
    Figure 12-4: The forces on the layer cut in saturated sand with a wedge.
    Screen Shot 2020-08-24 at 7.39.40 PM.png
    Figure 12-5: The forces on the wedge in saturated sand.
    Screen Shot 2020-08-24 at 7.40.21 PM.png
    Figure 12-6: The forces on the blade in saturated sand with a wedge.

    From equation (12-4) the forces on the pseudo blade can be derived. On the pseudo blade a force component in the direction of cutting velocity Fh and a force perpendicular to this direction Fv can be distinguished.

    \[\ \mathrm{F}_{\mathrm{h}}=-\mathrm{W}_{2} \cdot \sin (\theta)+\mathrm{K}_{2} \cdot \sin (\theta+\lambda)\tag{12-5}\]

    \[\ \mathrm{F}_{v}=-\mathrm{W}_{\mathrm{2}} \cdot \cos (\theta)+\mathrm{K}_{2} \cdot \cos (\theta+\lambda)\tag{12-6}\]

    The normal force on the shear plane A-B is now:

    \[\ \mathrm{N}_{1}=\frac{\mathrm{W}_{2} \cdot \sin (\lambda)+\mathrm{W}_{1} \cdot \sin (\theta+\beta+\lambda)}{\sin (\theta+\beta+\lambda+\varphi)} \cdot \cos (\varphi)\tag{12-7}\]

    The normal force on the pseudo blade A-C is now:

    \[\ \mathrm{N}_{2}=\frac{\mathrm{W}_{2} \cdot \sin (\theta+\beta+\varphi)+\mathrm{W}_{1} \cdot \sin (\varphi)}{\sin (\theta+\beta+\lambda+\varphi)} \cdot \cos (\lambda)\tag{12-8}\]

    Now the force equilibrium on the wedge has to be solved. This is done by first taking the horizontal and vertical force equilibrium on the wedge A-C-D.

    The horizontal equilibrium of forces:

    \[\ \mathrm{\sum F_{h}=+W_{4} \cdot \sin (\alpha)-K_{4} \cdot \sin \left(\alpha+\delta_{e}\right)+K_{3} \cdot \sin (\varphi)
    -W_{2} \cdot \sin (\theta)+K_{2} \cdot \sin (\theta+\lambda)=0}\tag{12-9}\]

    The vertical equilibrium of forces:

    \[\ \sum \mathrm{F}_{\mathrm{v}}=+\mathrm{W}_{4} \cdot \cos (\alpha)-\mathrm{K}_{4} \cdot \cos \left(\alpha+\delta_{\mathrm{e}}\right)+\mathrm{W}_{3}-\mathrm{K}_{3} \cdot \cos (\varphi)
    -\mathrm{W}_{2} \cdot \cos (\theta)+\mathrm{K}_{2} \cdot \cos (\theta+\lambda)=\mathrm{0}\tag{12-10}\]

    The grain force K3 on the bottom of the wedge is now:

    \[\ \mathrm{K}_{3}= \frac{-\mathrm{W}_{2} \cdot \sin \left(\alpha+\delta_{\mathrm{e}}-\theta\right)+\mathrm{K}_{2} \cdot \sin \left(\alpha+\delta_{\mathrm{e}}-\theta-\lambda\right)}{\sin \left(\alpha+\delta_{\mathrm{e}}+\varphi\right)}+\frac{+\mathrm{W}_{3} \cdot \sin \left(\alpha+\delta_{\mathrm{e}}\right)+\mathrm{W}_{4} \cdot \sin \left(\delta_{\mathrm{e}}\right)}{\sin \left(\alpha+\delta_{\mathrm{e}}+\varphi\right)} \tag{12-11}\]

    The grain force K4 on the blade is now:

    \[\ \begin{aligned} \mathrm{K}_{4}=& \frac{-\mathrm{W}_{2} \cdot \sin (\theta+\varphi)+\mathrm{K}_{2} \cdot \sin (\theta+\lambda+\varphi)}{\sin \left(\alpha+\delta_{\mathrm{e}}+\varphi\right)}+\frac{+\mathrm{W}_{3} \cdot \sin (\varphi)+\mathrm{W}_{4} \cdot \sin (\alpha+\varphi)}{\sin \left(\alpha+\delta_{\mathrm{e}}+\varphi\right)} \end{aligned}\tag{12-12}\]

    From equation (12-12) the forces on the pseudo blade can be derived. On the pseudo blade a force component in the direction of cutting velocity Fh and a force perpendicular to this direction Fv can be distinguished.

    \[\ \mathrm{F}_{\mathrm{h}}=-\mathrm{W}_{\mathrm{4}} \cdot \sin (\alpha)+\mathrm{K}_{4} \cdot \sin \left(\alpha+\delta_{\mathrm{e}}\right)\tag{12-13}\]

    \[\ \mathrm{F}_{\mathrm{v}}=-\mathrm{W}_{4} \cdot \cos (\alpha)+\mathrm{K}_{4} \cdot \cos \left(\alpha+\delta_{\mathrm{e}}\right)\tag{12-14}\]

    This page titled 12.2: The Equilibrium of Forces is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Sape A. Miedema (TU Delft Open Textbooks) via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.