12.4: The Equilibrium of Moments
- Page ID
- 29362
Based on the equilibrium of forces on the layer cut B-A-C, FEM calculations of pore water pressures and the minimum of cutting energy the forces N2, S2 and W2 are determined; see Miedema (1987 September). To determine the forces on the blade there are still a number of unknowns. W3 and W4 can be determined using FEM calculations of pore water pressures, given the wedge angle θ. Assuming λ=φ as a first estimate, the forces K3 and K4 depend on the wedge angle θ and on the effective external friction angle δe. For a static wedge, meaning that there is no movement between the wedge and the blade, the effective external friction angle can have a value between + and – the maximum external friction angle δ, so –δ<δe<δ. Combining this with the minimum energy principle results in a varying δe and a force N3 being equal to zero for a static wedge. The value of δe follows from the equilibrium of moments. For small values of the blade angle α, smaller than about 60o, the effective external friction angle δe=δ and most probably there will not be a wedge. For intermediate values of the blade angle α around 90o, there will be a static wedge and the effective external friction angle δe will decrease from +δ to –δ. For very large values of α, larger than about 120o, the effective external friction angle δe=–δ and N3 will have a positive value, meaning an upwards direction. Probably there will be a movement of soil under the blade. To find the value of the effective external friction angle first the equilibrium of moments has to be solved. Figure 12-18 shows the moments that occur on the wedge as a result of the forces and their acting points.
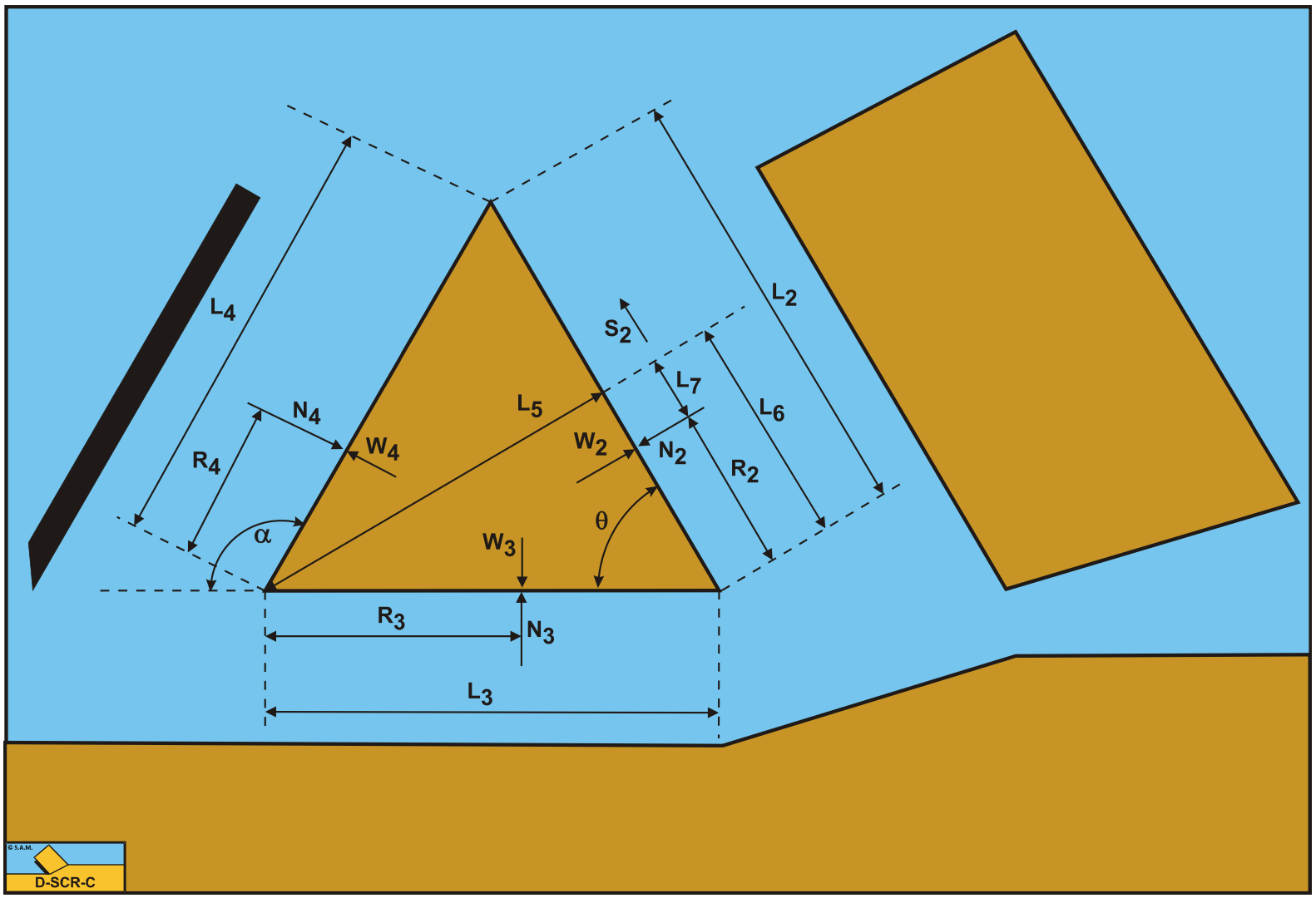
To determine the moment on the wedge, first the different lengths and distances have to be determined. The length of the shear plane A-B is:
\[\ \mathrm{A}-\mathrm{B}=\mathrm{L}_{1}=\frac{\mathrm{h}_{\mathrm{i}}}{\sin (\beta)}\tag{12-31}\]
The length of the pseudo blade or front of the wedge A-C is:
\[\ \mathrm{A}-\mathrm{C}=\mathrm{L}_{2}=\frac{\mathrm{h}_{\mathrm{b}}}{\sin (\theta)}\tag{12-32}\]
The length of the bottom of the wedge A-D is:
\[\ \mathrm{A}-\mathrm{D}=\mathrm{L}_{3}=\mathrm{h}_{\mathrm{b}} \cdot\left(\frac{1}{\tan (\theta)}-\frac{1}{\tan (\alpha)}\right)\tag{12-33}\]
The length of the blade D-C is:
\[\ \mathrm{D}-\mathrm{C}=\mathrm{L}_{4}=\frac{\mathrm{h}_{\mathrm{b}}}{\sin (\alpha)}\tag{12-34}\]
The distance between the blade edge and the wedge side A-C (perpendicular) is:
\[\ \mathrm{L}_{5}=\mathrm{L}_{3} \cdot \sin (\theta)\tag{12-35}\]
The distance from point A and the line L5 is:
\[\ \mathrm{L}_{6}=\mathrm{L}_{3} \cdot \cos (\theta)\tag{12-36}\]
The arm of the acting point of N2 and W2 is now:
\[\ \mathrm{L}_{7}=\mathrm{L}_{6}-\mathrm{R}_{2}\tag{12-37}\]
The equilibrium of moments can be determined using all those distances:
\[\ \sum \mathrm{M}=\left(\mathrm{N}_{4}-\mathrm{W}_{4}\right) \cdot \mathrm{R}_{4}-\left(\mathrm{N}_{3}-\mathrm{W}_{3}\right) \cdot \mathrm{R}_{3}+\left(\mathrm{N}_{2}-\mathrm{W}_{2}\right) \cdot \mathrm{L}_{7}-\mathrm{S}_{2} \cdot \mathrm{L}_{5}=\mathrm{0}\tag{12-38}\]
Equation (12-38) still contains the unknown arms R2, R3 and R4. Based on the FEM calculations for the pore pressures, values of 0.35·L2, 0.55·L3 and 0.32·L4 are found, Ma (2001). Figure 12-19 shows the moments on the wedge with respect to the cutting edge as a function of the wedge angle θ for different values of the shear angle β and a blade angle α of 90o. The moment is zero for a wedge angle θ between 50o and 55o.
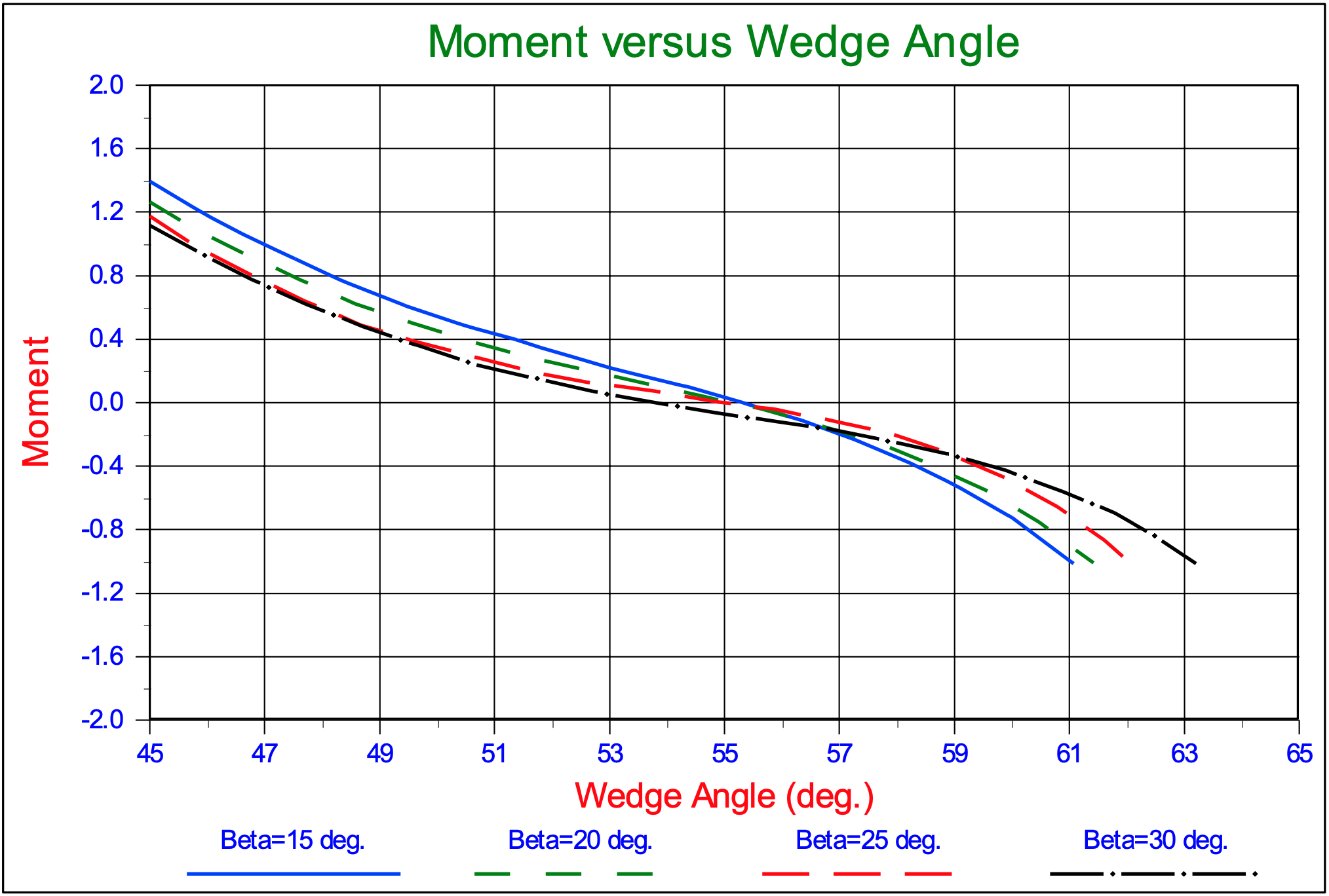
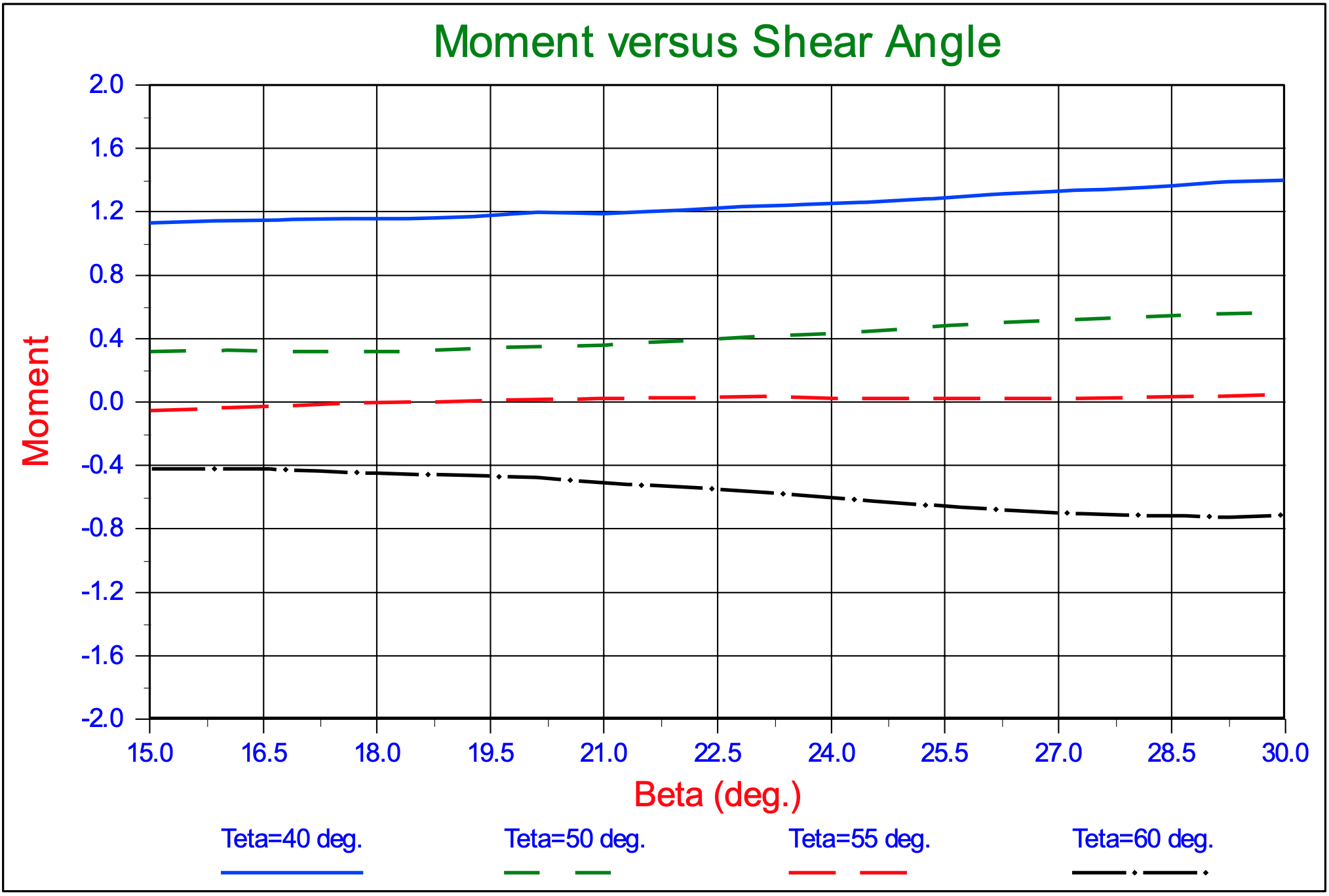
Figure 12-20 shows the moments as a function of the shear angle β for 4 values of the wedge angle θ. The moment is zero for the wedge angle θ=55o at a shear angle β=18o. It is clear from these figures that the shear angle where the moment is zero is not very sensitive for the shear angle and the wedge angle.
Figure 12-21 shows the force triangles on the 3 sides of the wedges for cutting angles from 60 to 120 degrees. From the calculations it appeared that the pore pressures on interface between the soil cut and the wedge and in the shear plane do not change significantly when the blade angle changes. These pore pressures p1m and p2m, resulting in the forces W1 and W2, are determined by the shear angle β, the wedge angle θ and other soil mechanical properties like the permeability.
The fact that the pore pressures do not significantly change, also results in forces K2, acting on the wedge that do not change significantly, according to equations (12-4), (12-5) and (12-6). These forces are shown in Figure 12-21 on the right side of the wedges and the figure shows that these forces are almost equal for all blade angles. These forces are determined by the conventional theory as published by Miedema (1987 September). Figure 12-21 also shows that for the small blade angles the friction force on the wedge is directed downwards, while for the bigger blade angles this friction force is directed upwards.
\[\ \mathrm{R}_{2}=\mathrm{e}_{2} \cdot \mathrm{L}_{2}, \quad \mathrm{R}_{3}=\mathrm{e}_{3} \cdot \mathrm{L}_{3}, \quad \mathrm{R}_{4}=\mathrm{e}_{4} \cdot \mathrm{L}_{4}\tag{12-39}\]
Now the question is, what is the solution for the cutting of water saturated sand at large cutting angles? From many calculations and an analysis of the laboratory research is described by He (1998), Ma (2001) and Miedema (2005), it appeared that the wedge can be considered a static wedge, although the sand inside the wedge still may have velocity, the sand on the blade is not moving. The main problem in finding acceptable solutions was finding good values for the acting points on the 3 sides of the wedge, e2, e3 and e4. If these values are chosen right, solutions exist based on the equilibrium of moments, but if they are chosen wrongly, no solution will be found. So the choice of these parameters is very critical. The statement that the sand on the blade is not moving is based on two things, first of all if the sand is moving with respect to the blade, the soil interface friction is fully mobilized and the bottom of the wedge requires to have a small angle with respect to the horizontal in order to make a flow of sand possible. This results in much bigger cutting forces, while often no solution can be found or unreasonable values for e2, e3 and e4 have to be used to find a solution.
So the solution is, using the equilibrium equations for the horizontal force, the vertical force and the moments on the wedge. The recipe to determine the cutting forces seems not to difficult now, but it requires a lot of calculations and understanding of the processes, because one also has to distinguish between the theory for small cutting angles and the wedge theory.
The following steps have to be taken to find the correct solution:
-
Determine the dimensionless pore pressures p1m, p2m, p3m and p4m using a finite element calculation or the method described by Miedema (2006B), for a variety of shear angles β and wedge angles θ around the expected solution.
-
Determine the shear angle β based on the equilibrium equations for the horizontal and vertical forces, a given wedge angle θ and the principle of minimum energy, which is equivalent to the minimum horizontal force.
This also gives a value for the resulting force K2 acting on the wedge. -
Determine values of e2, e3 and e4 based on the results from the pore pressure calculations.
-
Determine the solutions of the equilibrium equations on the wedge and find the solution which has the minimum energy dissipation, resulting in the minimum horizontal force on the blade.
-
Determine the forces without a wedge with the theory for small cutting angles.
-
Determine which horizontal force is the smallest, with or without the wedge.



