12.7: Limits
- Page ID
- 35012
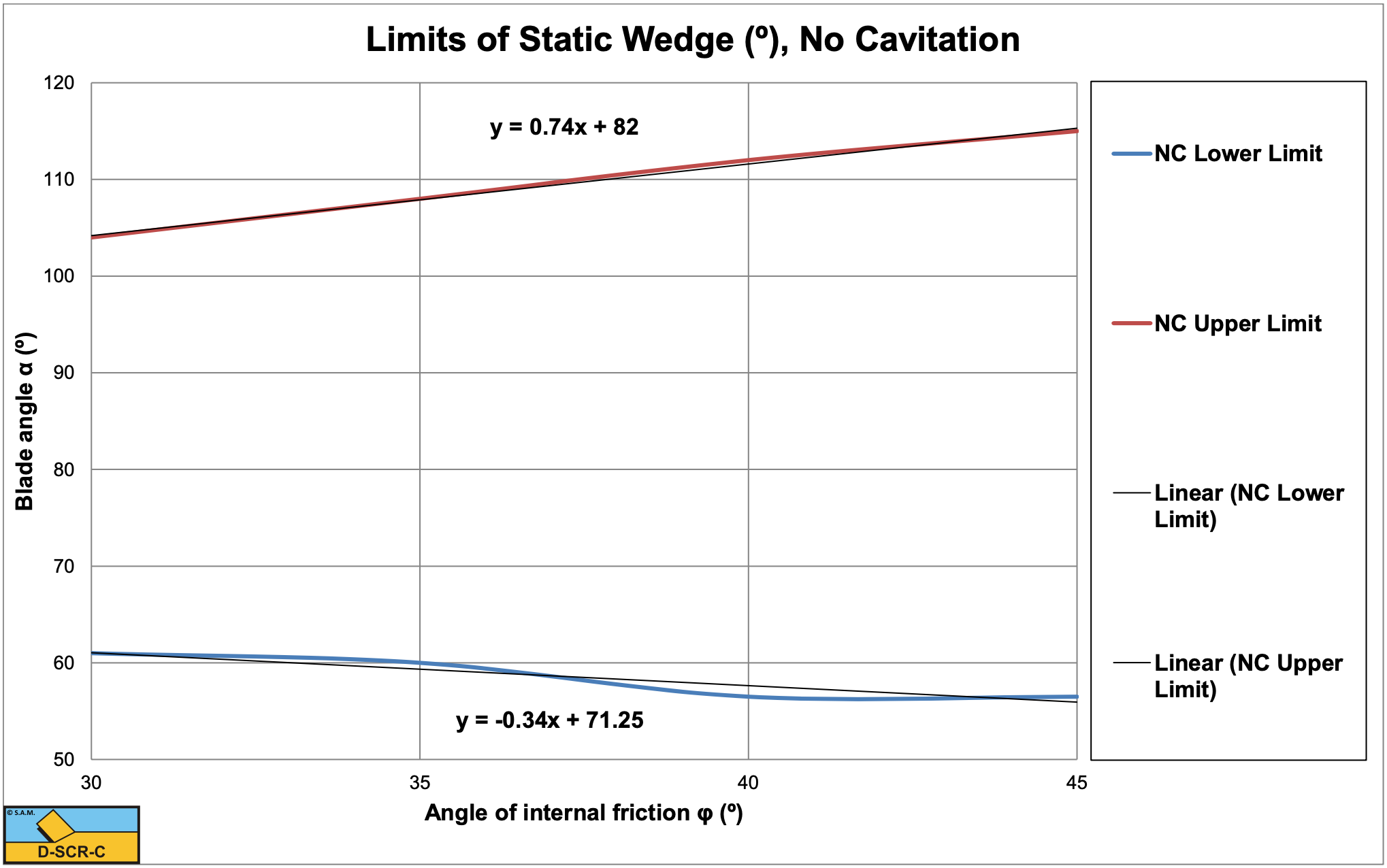
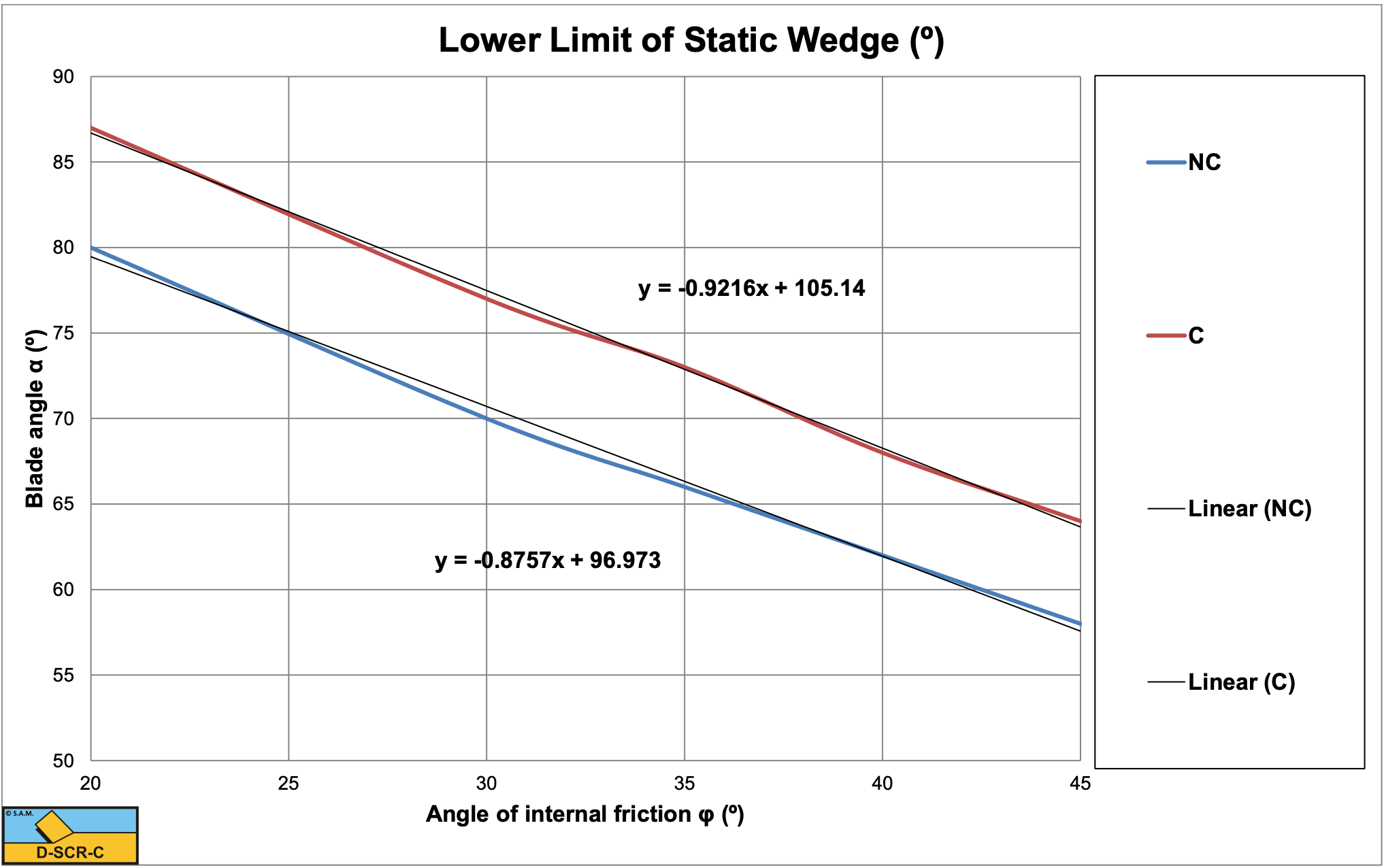
Instead of carrying out the calculations for each different case, the limits of the occurrence of the wedge can be summarized in a few graphs. Figure 12-26 shows the upper and lower limit of the wedge for the non-cavitating case as a function of the angle of internal friction φ. It can be concluded that the upper and lower limits are not symmetrical around 90o, but a bit lower than that. An increasing angle of internal friction results in a larger bandwidth for the occurrence of the wedge. For blade angles above the upper limit most probably subduction will occur, although there is no scientific evidence for this. The theory developed should not be used for blade angles above the upper limit yet. Further research is required. The lower limit is not necessarily the start of the occurrence of the wedge. This depends on whether the cutting forces with the wedge are smaller than the cutting forces without the wedge. Figure 12-28 shows the blade angle where the wedge will start to occur, based on the minimum of the horizontal cutting forces with and without the wedge. It can be concluded that the blade angle where the wedge starts to occur is larger than the minimum where the wedge can exist, which makes sense. For high angles of internal friction, the starting blade angle is about equal to the lower limit.
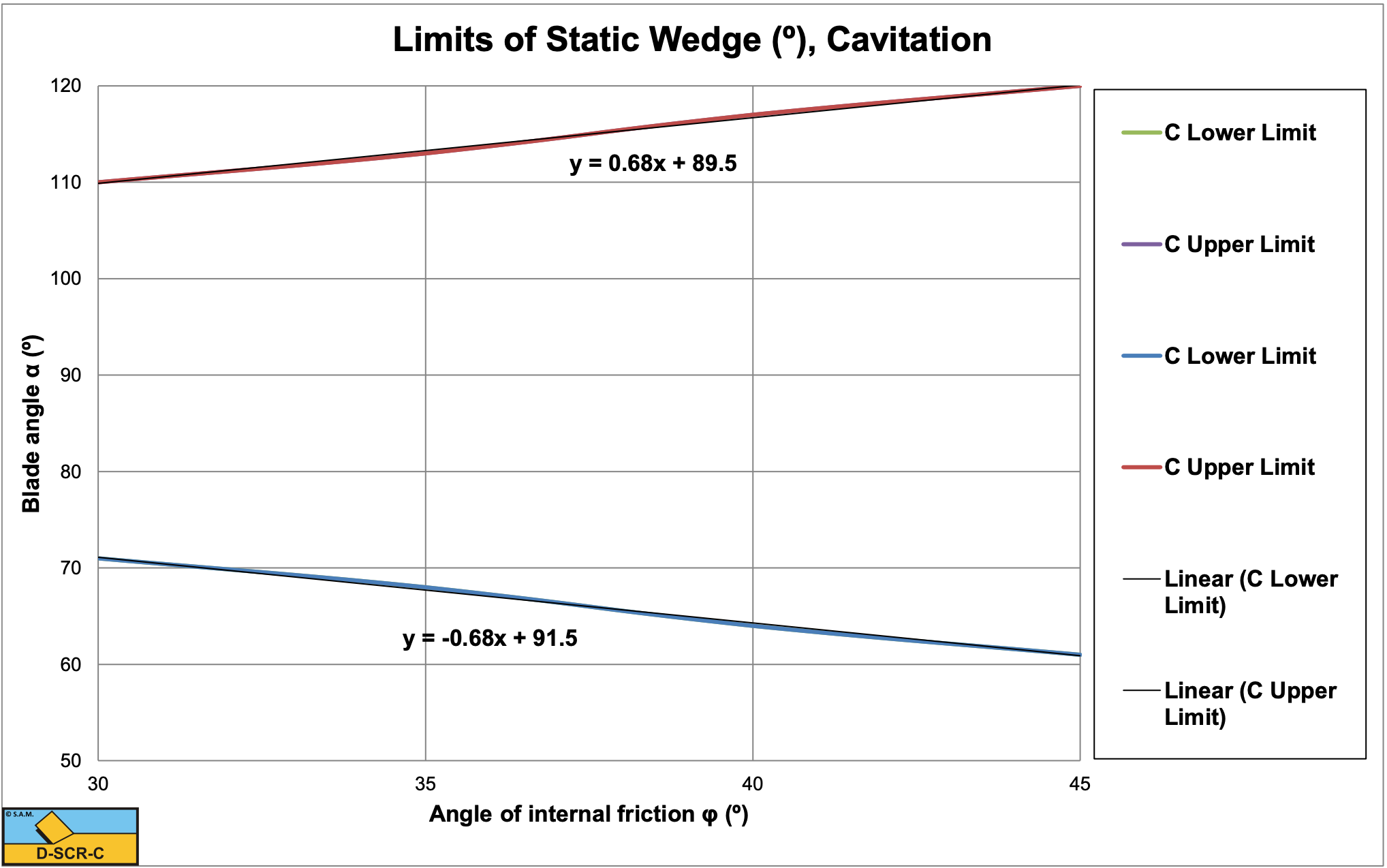
For the cavitating case the upper and lower limit are shown in Figure 12-27. In this case the limits are symmetrical around 90o and with an external friction angle of 2/3 of the internal friction angle it can be concluded that these limits are 90o+δ and 90o-δ. The blade angle where the wedge will start to occur is again shown in Figure 12-28.
The methodology applied gives satisfactory results to determine the cutting forces at large cutting angles. The results shown in this paper are valid for the non-cavitating and the cavitating cutting process and for the soils and geometry as used in this paper. The wedge angles found are, in general, a bit smaller then 90o-δ for the non- cavitating case and exactly 90o-δ for the cavitating case, so as a first approach this can be used.
The mobilized external friction angle δe varies from plus the maximum for small blade angles to minus the maximum for large blade angles, depending on the blade angle.
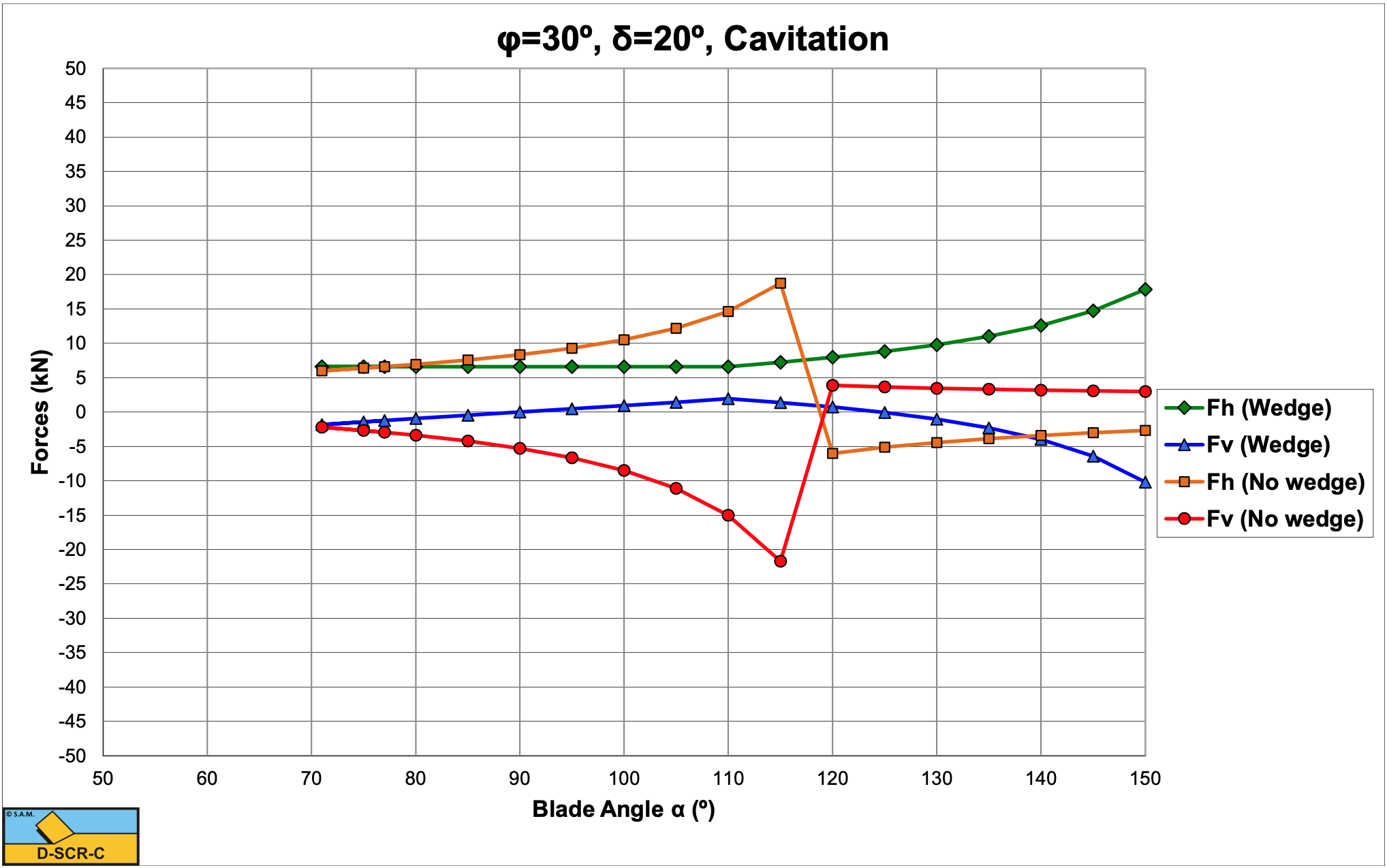
The cutting forces with the wedge do not increase much in the non-cavitating case and not at all in the cavitating case, when the cutting angle increases from 60o to 120o.
If the ratio between the thickness of the layer cut and the blade height changes, also the values of the acting points e2, e3 and e4 will change slightly.
It is not possible to find an explicit analytical solution for the wedge problem and it’s even difficult to automate the calculation method, since the solution depends strongly on the values of the acting points.
Figure 12-26, Figure 12-27 and Figure 12-28 are a great help determining whether or not a wedge will occur and at which blade angle it will start to occur.
The theory developed can be applied to cutting processes of bulldozers, in front of the heel of a drag head, ice scour, tunnel boring machines and so on.