14.3: The Equilibrium of Moments
- Page ID
- 29375
In order to solve the problem, also the equilibrium of moments is required, since the wedge is not subject to rotational acceleration. The equilibrium of moments can be taken around each point of the wedge. Here the tip of the blade is chosen. The advantage of this is that a number of forces do not contribute to the moments on the wedge.
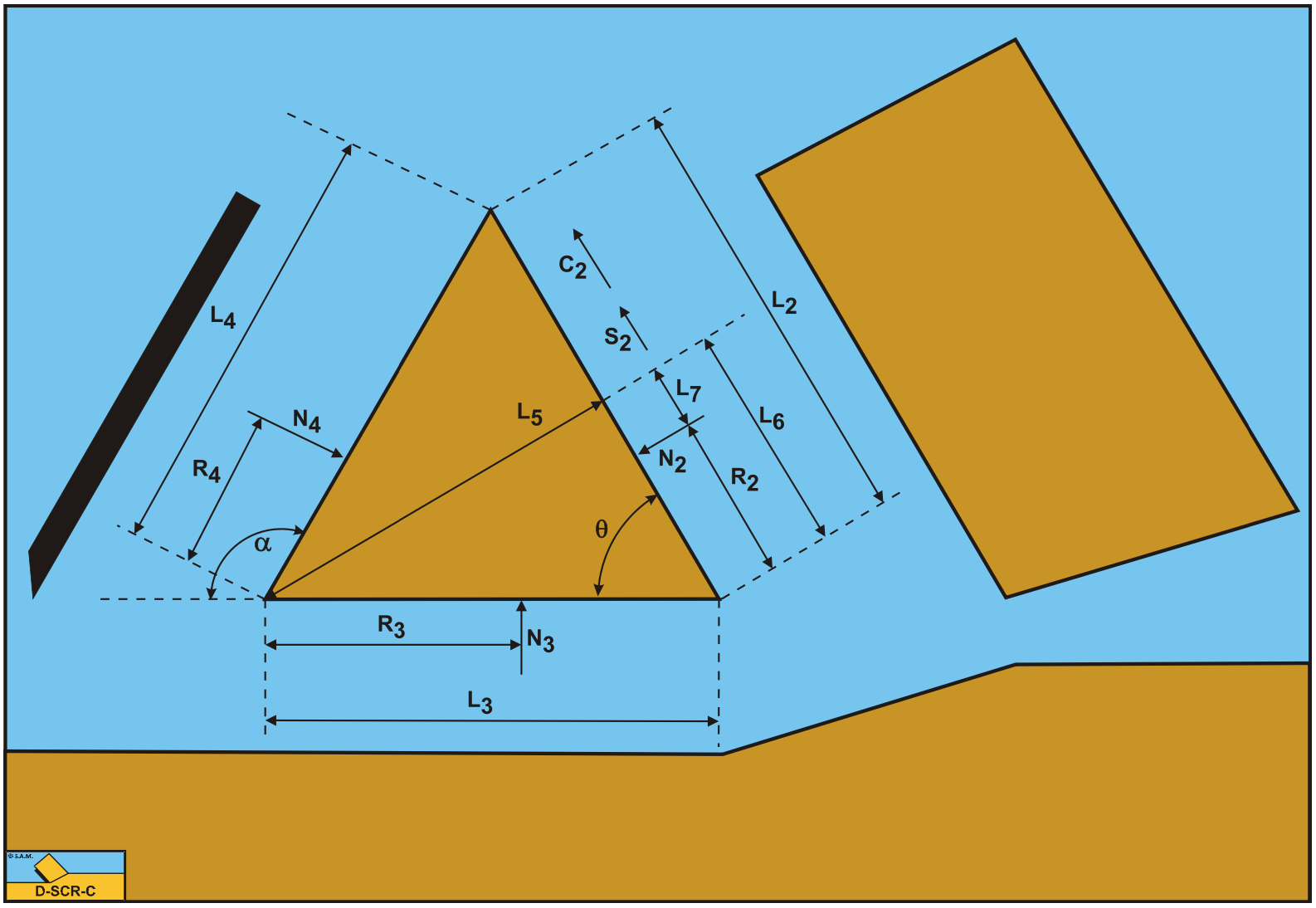
In order to derive the equilibrium of moments equation the arms of all the forces contributing to this equilibrium have to be known. Since these arms depend on the length of all the sides in the cutting process, first these lengths are determined. The length of the shear plane A-B is:
\[\ \mathrm{L}_{1}=\frac{\mathrm{h}_{\mathrm{i}}}{\sin (\beta)}\tag{14-19}\]
The length of the pseudo blade A-C is:
\[\ \mathrm{L}_{2}=\frac{\mathrm{h}_{\mathrm{b}}}{\sin (\theta)}\tag{14-20}\]
The length of the bottom of the wedge A-D is:
\[\ \mathrm{L}_{3}=\mathrm{h}_{\mathrm{b}} \cdot\left(\frac{\mathrm{1}}{\tan (\theta)}-\frac{1}{\tan (\alpha)}\right)\tag{14-21}\]
The length of the blade C-D is:
\[\ \mathrm{L}_{4}=\frac{\mathrm{h}_{\mathrm{b}}}{\sin (\alpha)}\tag{14-22}\]
The length of the line from the tip of the blade to the opposite side of the wedge and perpendicular to this side is:
\[\ \mathrm{L}_{5}=\mathrm{L}_{3} \cdot \sin (\theta)\tag{14-23}\]
The length of the line from point A to the intersection point of the previous line with side A-C is:
\[\ \mathrm{L}_{\mathrm{6}}=\mathrm{L}_{\mathrm{3}} \cdot \cos (\theta)\tag{14-24}\]
The distance from the acting point of the pore pressure force on side A-C to the intersection point of the previous line with side A-C is:
\[\ \mathrm{L}_{7}=\mathrm{L}_{6}-\mathrm{R}_{2}\tag{14-25}\]
The values of the acting points R2, R3 and R4 follow from calculated or estimated stress distributions.
The equilibrium of moments is now:
\[\ \sum \mathrm{M}=\mathrm{N}_{4} \cdot \mathrm{R}_{4}-\mathrm{N}_{3} \cdot \mathrm{R}_{3}+\mathrm{N}_{2} \cdot \mathrm{L}_{7}-\left(\mathrm{S}_{2}+\mathrm{C}_{2}\right) \cdot \mathrm{L}_{5}=\mathrm{0}\tag{14-26}\]


