2.7: Probability of connectivity

Last updated
Save as PDF

Page ID: 46582

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Figure \(\PageIndex{1}\): Probability of connectivity with n=10 and a range of p. The vertical line shows the predicted critical value.

Figure \(\PageIndex{2}\): Probability of connectivity for several values of n and a range of p.

For given values of n and p, we would like to know the probability that G(n, p) is connected. We can estimate it by generating a large number of random graphs and counting how many are connected. Here’s how:

def prob_connected(n, p, iters=100): 
    tf = [is_connected(make_random_graph(n, p)) 
        for i in range(iters)] 
    return np.mean(bool)

The parameters n and p are passed along to make_random_graph; iters is the number of random graphs we generate.

This function uses a list comprehension; if you are not familiar with this feature, you can read about it at http://thinkcomplex.com/comp.

The result, tf, is a list of boolean values: True for each graph that’s connected and False for each one that’s not.

np.mean is a NumPy function that computes the mean of this list, treating True as 1 and False as 0. The result is the fraction of random graphs that are connected.

>>> prob_connected(10, 0.23, iters=10000) 
0.33

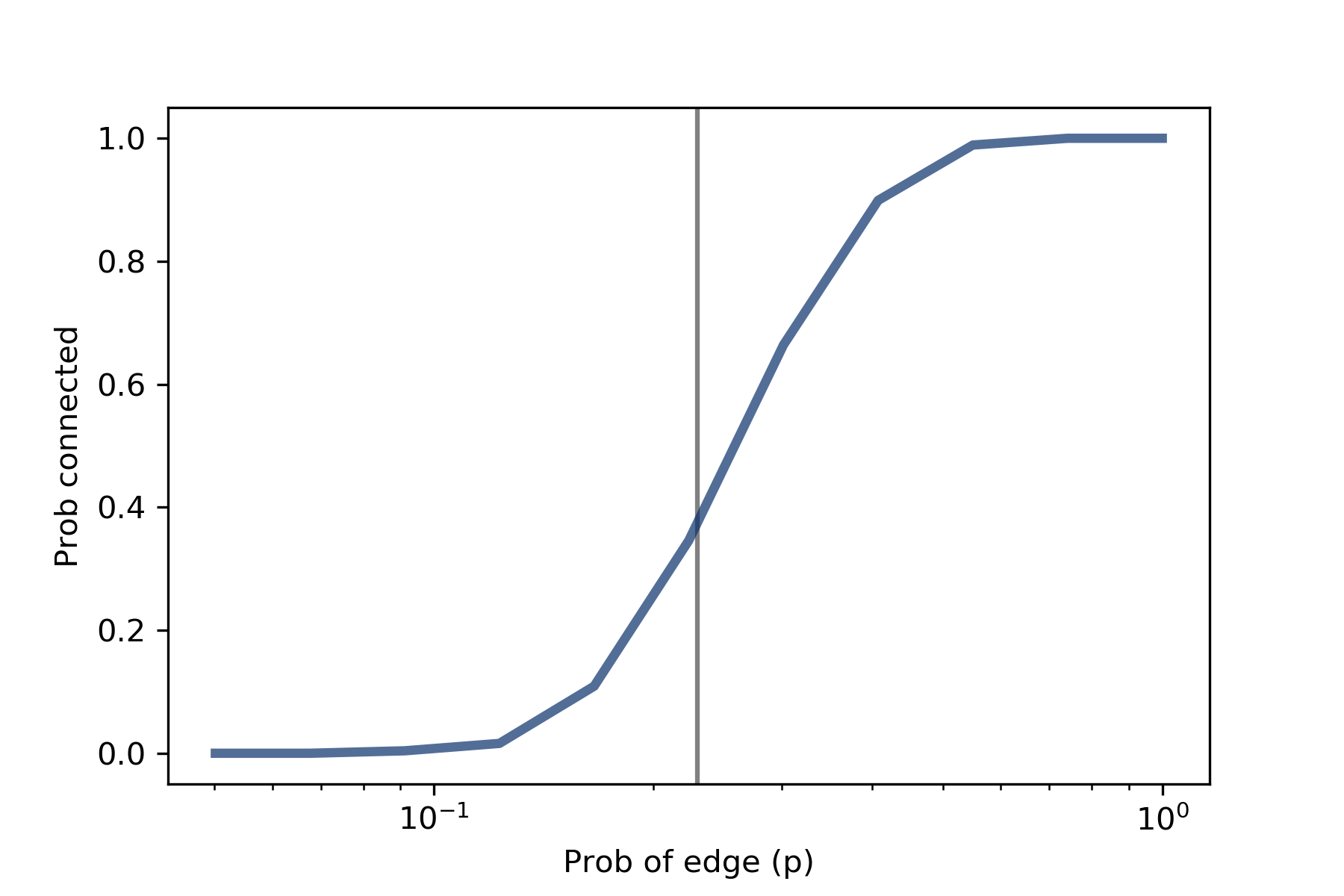
I chose 0.23 because it is close to the critical value where the probability of connectivity goes from near 0 to near 1. According to Erdős and Rényi, p^* = lnn / n = 0.23.

We can get a clearer view of the transition by estimating the probability of connectivity for a range of values of p:

n = 10 
ps = np.logspace(-2.5, 0, 11) 
ys = [prob_connected(n, p) for p in ps]

The NumPy function logspace returns an array of 11 values from 10^−2.5 to 10⁰ = 1, equally spaced on a logarithmic scale.

For each value of p in the array, we compute the probability that a graph with parameter p is connected and store the results in ys.

Figure \(\PageIndex{1}\) shows the results, with a vertical line at the computed critical value, p^* = 0.23. As expected, the transition from 0 to 1 occurs near the critical value.

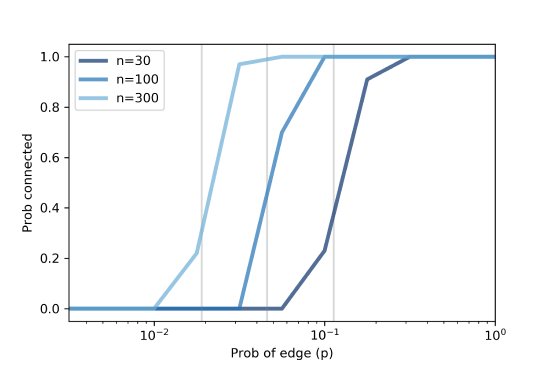
Figure \(\PageIndex{2}\) shows similar results for larger values of n. As n increases, the critical value gets smaller and the transition gets more abrupt.

These experimental results are consistent with the analytic results Erdős and Rényi presented in their papers.