1.8.1: Problem Set
- Page ID
- 9480
Write a script to plot function \(y=\frac{\sin (x)}{x}\) for \(\frac{\pi}{100} \leq x \leq 10 \pi\) using increments of \(\frac{\pi}{100}\). Publish your m-file to html.
- Answer
-
The m-file content: % This script plots a graph of Graph of y=sin(x)/x clc % Clear screen x = pi/100:pi/100:10*pi; % Create a row vector y = sin(x)./x; % Calculate y as function of x plot(x,y),title('Graph of y=sin(x)/x'),xlabel('x'),ylabel('y'),grid. The html output:
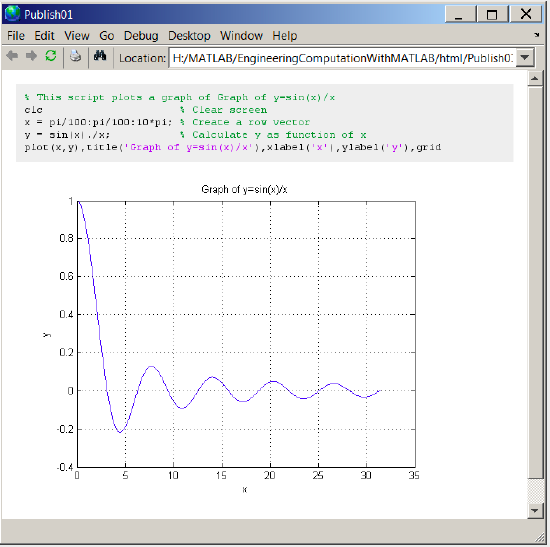
Figure \(\PageIndex{1}\). The published html file.
A gas is expanded in an engine cylinder, following the law PV1.3=c. The initial pressure is 2550 kPa and the final pressure is 210 kPa. If the volume at the end of expansion is 0.75 m3, write a script to compute the work done by the gas and publish your solution to an html file. This is the same problem as this Problem you have solved before.
- Answer
-
The m-file content: clc disp('A gas is expanded in an engine cylinder, following the law PV^1.3=c') disp('The initial pressure is 2550 kPa and the final pressure is 210 kPa.') disp('If the volume at the end of expansion is 0.75 m3,') disp('Compute the work done by the gas.') disp(' ') % Display blank line n=1.3; P_i=2550; % Initial pressure P_f=210; % Final pressure V_f=.75; % Final volume V_i=(P_f*(V_f^n)/P_i)^(1/n); % Initial volume c=P_f*V_f^n; v=V_i:.001:V_f; % Creating a row vector for volume, v p=c./(v.^n); % Computing pressure for volume WorkDone=trapz(v,p) % Integrating p*dv
The html output:
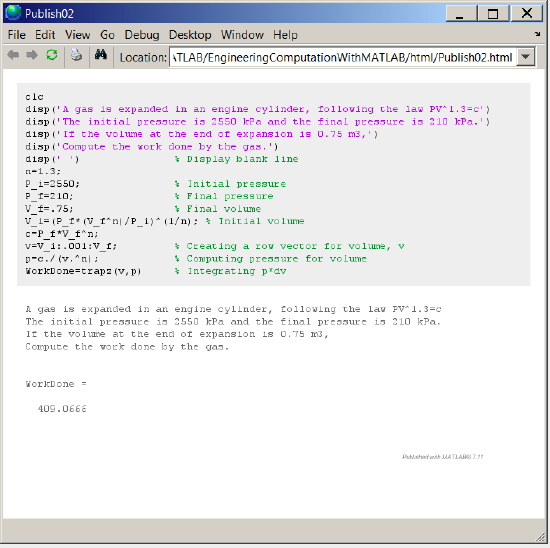
Figure \(\PageIndex{1}\). The published html file.
A force F acting on a body at a distance s from a fixed point is given by \(F=3 s+\frac{1}{s^{2}}\). Write a script to compute the work done when the body moves from the position where s=1 to that where s=10 and and publish your solution to an html file. Include a table of contents in the output file. This is the same problem as this Problem you have solved before.
- Answer
-
The m-file content: %% Work done % This script computes the work done on an object clc disp('A force F acting on a body at a distance s from a fixed point is given by') disp('F=3*s+(1/(s^2)) where s is the distance in meters') disp('Compute the total work done in moving') disp('From the position where s=1 to that where s=10.') disp(' ') % Display blank line %% Create a row vector for distance, s s=1:.001:10; %% Compute Force for s F=3.*s+(1./(s.^2)); % Computing Force for s %% Integrating F*ds over 1 to 10 meters. WorkDone=trapz(s,F) The html output:
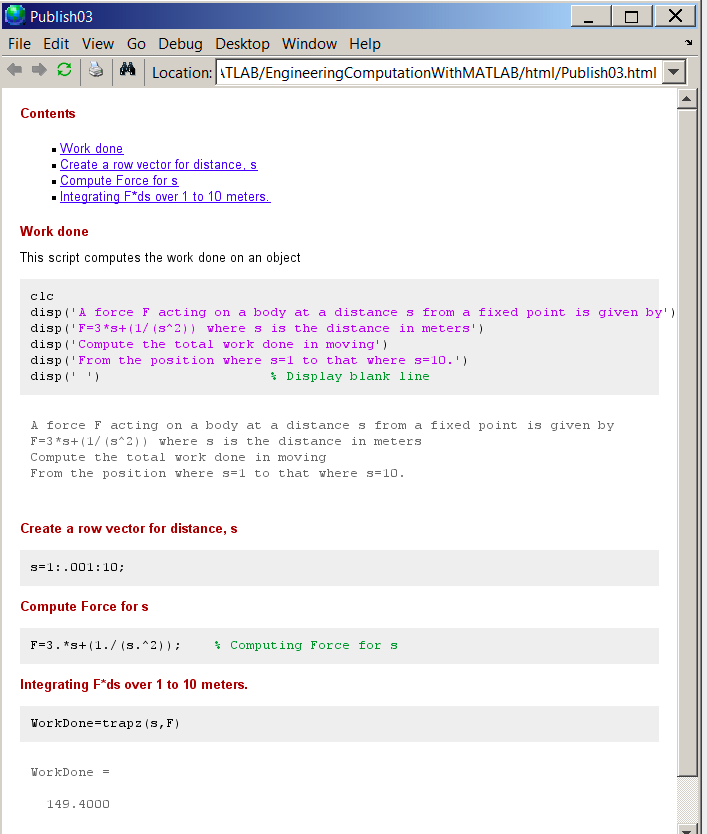
Figure \(\PageIndex{3}\). The published html file.


