7.2: Lighting and Material
- Page ID
- 13746
In this section, we turn to the question of lighting and material in WebGL. We will continue to use the basic OpenGL model that was covered in Section 4.1 and Section 4.2, but now we are responsible for implementing the lighting equation in our own GLSL shader programs. That means being more aware of the implementation details. It also means that we can pick and choose which parts of the lighting equation we will implement for a given application.
The goal of the lighting equation is to compute a color for a point on a surface. The inputs to the equation include the material properties of the surface and the properties of light sources that illuminate the surface. The angle at which the light hits the surface plays an important role. The angle can be computed from the direction to the light source and the normal vector to the surface. Computation of specular reflection also uses the direction to the viewer and the direction of the reflected ray. The four vectors that are used in the computation are shown in this lighting diagram from Subsection 4.1.4:
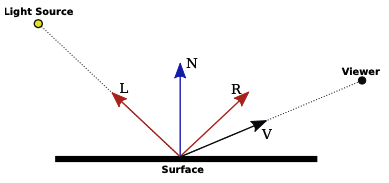
The vectors L, N, R, and V should be unit vectors. Recall that unit vectors have the property that the cosine of the angle between two unit vectors is given by the dot product of the two vectors.
The lighting equation also involves ambient and emission color, which do not depend the direction vectors shown in the diagram.
You should keep this big picture in mind as we work through some examples that use various aspects of the lighting model.
Minimal Lighting
Even very simple lighting can make 3D graphics look more realistic. For minimal lighting, I sometimes use what I call a “viewpoint light,” a white light that shines from the direction of the viewer into the scene. In the simplest case, a directional light can be used. In eye coordinates, a directional viewpoint light shines in the direction of the negative z-axis. The light direction vector (L in the above diagram), which points towards the light source, is (0,0,1).
To keep things minimal, let’s consider diffuse reflection only. In that case, the color of the light reflected from a surface is the product of the diffuse material color of the surface, the color of the light, and the cosine of the angle at which the light hits the surface. The product is computed separately for the red, green, and blue components of the color. We are assuming that the light is white, so the light color is 1 in the formula. The material color will probably come from the JavaScript side as a uniform or attribute variable.
The cosine of the angle at which the light hits the surface is given by the dot product of the normal vector N with the light direction vector L. In eye coordinates, L is (0,0,1). The dot product, \( N \cdot L \) or \( N \cdot (0,0,1) \), is therefore simply N.z, the z-component of N. However, this assumes that N is also given in eye coordinates. The normal vector will ordinarily come from the JavaScript side and will be expressed in object coordinates. Before it is used in lighting calculations, it must be transformed to the eye coordinate system. As discussed in Subsection 7.1.4, to do that we need a normal transformation matrix that is derived from the modelview matrix. Since the normal vector must be of length one, the GLSL code for computing N would be something like
vec3 N = normalize( normalMatrix * normal );
where normal is the original normal vector in object coordinates, normalMatrix is the normal transformation matrix, and normalize is a built-in GLSL function that returns a vector of length one pointing in the same direction as its parameter.
There is one more complication: The dot product \( N \cdot L \) can be negative, which would mean that the normal vector points away from the light source (into the screen in this case). Ordinarily, that would mean that the light does not illuminate the surface. In the case of a viewpoint light, where we know that every visible surface is illuminated, it means that we are looking at the “back side” of the surface (or that incorrect normals were specified). Let’s assume that we want to treat the two sides of the surface the same. The correct normal vector for the back side is the negative of the normal vector for the front side, and the correct dot product is \( (-N) \cdot L \). We can handle both cases if we simply use \( abs(N \cdot L) \). For \( L = (0,0,1) \), that would be \( abs(N.z) \). If color is a vec3 giving the diffuse color of the surface, the visible color can be computed as
vec3 visibleColor = abs(N.z) * color;
If color is instead a vec4 giving an RGBA color, only the RGB components should be multiplied by the dot product:
vec4 visibleColor = vec4( abs(N.z)*color.rgb, color.a );
The sample program webgl/cube-with-basic-lighting.html implements this minimal lighting model. The lighting calculations are done in the vertex shader. Part of the scene is drawn without lighting, and the vertex shader has a uniform bool variable to specify whether lighting should be applied. Here is the vertex shader source code from that program:
attribute vec3 a_coords; // Object coordinates for the vertex.
uniform mat4 modelviewProjection; // Combined transformation matrix.
uniform bool lit; // Should lighting be applied?
uniform vec3 normal; // Normal vector (in object coordinates).
uniform mat3 normalMatrix; // Transformation matrix for normal vectors.
uniform vec4 color; // Basic (diffuse) color.
varying vec4 v_color; // Color to be sent to fragment shader.
void main() {
vec4 coords = vec4(a_coords,1.0);
gl_Position = modelviewProjection * coords;
if (lit) {
vec3 N = normalize(normalMatrix*normal); // Transformed unit normal.
float dotProduct = abs(N.z);
v_color = vec4( dotProduct*color.rgb, color.a );
}
else {
v_color = color;
}
}
It would be easy to add ambient light to this model, using a uniform variable to specify the ambient light level. Emission color is also easy.
The directional light used in this example is technically only correct for an orthographic projection, although it will also generally give acceptable results for a perspective projection. But the correct viewpoint light for a perspective projection is a point light at (0,0,0) — the position of the “eye” in eye coordinates. A point light is a little more difficult than a directional light.
Remember that lighting calculations are done in eye coordinates. The vector L that points from the surface to the light can be computed as
vec3 L = normalize( lightPosition - eyeCoords.xyz );
where lightPosition is a vec3 that gives the position of the light in eye coordinates, and eyeCoords is a vec4 giving the position of the surface point in eye coordinates. For a viewpoint light, the lightPosition is (0,0,0), and L can be computed simply as normalize(−eyeCoords.xyz). The eye coordinates for the surface point must be computed by applying the modelview matrix to the object coordinates for that point. This means that the shader program needs to know the modelview matrix; it’s not sufficient to know the combined modelview and projection matrix. The vertex shader shown above can modified to use a point light at (0,0,0) as follows:
attribute vec3 a_coords; // Object coordinates for the vertex.
uniform mat4 modelview; // Modelview transformation matrix
uniform mat4 projection; // Projection transformation matrix.
uniform bool lit; // Should lighting be applied?
uniform vec3 normal; // Normal vector (in object coordinates).
uniform mat3 normalMatrix; // Transformation matrix for normal vectors.
uniform vec4 color; // Basic (diffuse) color.
varying vec4 v_color; // Color to be sent to fragment shader.
void main() {
vec4 coords = vec4(a coords,1.0);
vec4 eyeCoords = modelview * coords;
gl_Position = projection * eyeCoords;
if (lit) {
vec3 L = normalize( - eyeCoords.xyz ); // Points to light.
vec3 N = normalize(normalMatrix*normal); // Transformed unit normal.
float dotProduct = abs( dot(N,L) );
v_color = vec4( dotProduct*color.rgb, color.a );
}
else {
v_color = color;
}
}
(Note, however, that in some situations, it can be better to move the lighting calculations to the fragment shader, as we will soon see.)
Specular Reflection and Phong Shading
To add specular lighting to our basic lighting model, we need to work with the vectors R and V in the lighting diagram. In perfect specular reflection, the viewer sees a specular highlight only if R is equal to V, which is very unlikely. But in the lighting equation that we are using, the amount of specular reflection depends on the dot product \( R \cdot V \), which represents the cosine of the angle between R and V. The formula for the contribution of specular reflection to the visible color is
\( (R \cdot V)^{s} * specularMaterialColor * lightIntensity \)
where s is the specular exponent (the material property called “shininess” in OpenGL). The formula is only valid if \( R \cdot V \) is greater than zero; otherwise, the specular contribution is zero.
The unit vector R can be computed from L and N. (Some trigonometry shows that R is given by \( 2*(N \cdot L)*N - L. \)). GLSL has a built-in function reflect(I,N) that computes the reflection of a vector I through a unit normal vector N; however, the value of reflect (L,N) is −R rather than R. (GLSL assumes a light direction vector that points from the light toward the surface, while my L vector does the reverse.)
The unit vector V points from the surface towards the position of the viewer. Remember that we are doing the calculations in eye coordinates. For an orthographic projection, the viewer is essentially at infinite distance, and V can be taken to be (0,0,1). For a perspective projection, the viewer is at the point (0,0,0) in eye coordinates, and V is given by normalize(−eyeCoords) where eyeCoords contains the xyz coordinates of the surface point in the eye coordinate system. Putting all this together, and assuming that we already have N and L, the GLSL code for computing the color takes the form:
R = -reflect(L,N);
V = normalize( -eyeCoords.xyz ); // (Assumes a perspective projection.)
vec3 color = dot(L,N) * diffuseMaterialColor.rgb * diffuseLightColor;
if (dot(R,V) > 0.0) {
color = color + ( pow(dot(R,V),specularExponent) *
specularMaterialColor * specularLightColor );
}
The sample program webgl/basic-specular-lighting.html implements lighting with diffuse and specular reflection. For this program, which draws curved surfaces, normal vectors are given as a vertex attribute rather rather than a uniform variable. To add some flexibility to the lighting, the light position is specified as a uniform variable rather than a constant. Following the OpenGL convention, lightPosition is a vec4. For a directional light, the w-coordinate is 0, and the eye coordinates of the light are lightPosition.xyz. If the w-coordinate is non-zero, the light is a point light, and its eye coordinates are lightPosition.xyz/lightPosition.w. (The division by lightPosition.w is the convention for homogeneous coordinates, but in practice, lightPosition.w will usually be either zero or one.) The program allows for different diffuse and specular material colors, but the light is always white, with diffuse intensity 0.8 and specular intensity 0.4. You should be able to understand all of the code in the vertex shader:
attribute vec3 a_coords;
attribute vec3 a_normal;
uniform mat4 modelview;
uniform mat4 projection;
uniform mat3 normalMatrix;
uniform vec4 lightPosition;
uniform vec4 diffuseColor;
uniform vec3 specularColor;
uniform float specularExponent;
varying vec4 v_color;
void main() {
vec4 coords = vec4(a_coords,1.0);
vec4 eyeCoords = modelview * coords;
gl_Position = projection * eyeCoords;
vec3 N, L, R, V; // Vectors for lighting equation.
N = normalize( normalMatrix*a_normal );
if ( lightPosition.w == 0.0 ) { // Directional light.
L = normalize( lightPosition.xyz );
}
else { // Point light.
L = normalize( lightPosition.xyz/lightPosition.w - eyeCoords.xyz );
}
R = -reflect(L,N);
V = normalize( -eyeCoords.xyz); // (Assumes a perspective projection.)
if ( dot(L,N) <= 0.0 ) {
v_color = vec4(0,0,0,1); // The vertex is not illuminated.
}
else {
vec3 color = 0.8 * dot(L,N) * diffuseColor.rgb;
if (dot(R,V) > 0.0) {
color += 0.4 * pow(dot(R,V),specularExponent) * specularColor;
}
v_color = vec4(color, diffuseColor.a);
}
}
The fragment shader just assigns the value of v color to gl_FragColor.
This approach imitates OpenGL 1.1 in that it does lighting calculations in the vertex shader. This is sometimes called per-vertex lighting. It is similar to Lambert shading in three.js, except that Lambert shading only uses diffuse reflection. But there are many cases where per-vertex lighting does not give good results. We saw in Subsection 5.1.4 that it can give very bad results for spotlights. It also tends to produce bad specular highlights, unless the primitives are very small.
If a light source is close to a primitive, compared to the size of the primitive, the the angles that the light makes with the primitive at the vertices can have very little relationship to the angle of the light at an interior point of the primitive:
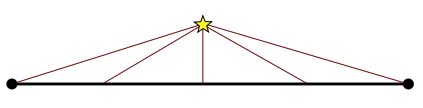
Since lighting depends heavily on the angles, per-vertex lighting will not give a good result in this case. To get better results, we can do per-pixel lighting. That is, we can move the lighting calculations from the vertex shader into the fragment shader.
To do per-pixel lighting, certain data that is available in the vertex shader must be passed to the fragment shader in varying variables. This includes, for example, either object coordinates or eye coordinates for the surface point. The same might apply to properties such as diffuse color, if they are attributes rather then uniform variables. Of course, uniform variables are directly accessible to the fragment shader. Light properties will generally be uniforms, and material properties might well be.
And then, of course, there are the normal vectors, which are so essential for lighting. Al- though normal vectors can sometimes be uniform variables, they are usually attributes. Per- pixel lighting generally uses interpolated normal vectors, passed to the fragment shader in a varying variable. (Phong shading is just per-pixel lighting using interpolated normals.) An interpolated normal vector is in general only an approximation for the geometrically correct normal, but it’s usually good enough to give good results. Another issue is that interpolated normals are not necessarily unit vectors, even if the normals in the vertex shader are unit vec- tors. So, it’s important to normalize the interpolated normal vectors in the fragment shader. The original normal vectors in the vertex shader should also be normalized, for the interpolation to work properly.
The sample program webgl/basic-specular-lighting-Phong.html uses per-pixel lighting. I urge you to read the shader source code in that program. Aside from the fact that lighting calculations have been moved to the fragment shader, it is identical to the previous sample program.
The on-line demo c7/per-pixel-vs-per-vertex.html lets you view objects drawn using per-vertex lighting side-by-side with objects drawn using per-pixel lighting. It uses the same shader programs as the two sample programs. Here is an example from that demo:

For this cylinder, all of the vertices are along the top and bottom edges, and the light source is fairly close to the cylinder. In this example, per-pixel lighting misses the specular highlight entirely.
Adding Complexity
Our shader programs are getting more complex. As we add support for multiple lights, additional light properties, two-sided lighting, textures, and other features, it will be useful to use data structures and functions to help manage the complexity. GLSL data structures were introduced in Subsection 6.3.2, and functions in Subsection 6.3.5. Let’s look briefly at how they can be used to work with light and material.
It makes sense to define a struct to hold the properties of a light. The properties will usually include, at a minimum, the position and color of the light. Other properties can be added, depending on the application and the details of the lighting model that are used. For example, to make it possible to turn lights on and off, a bool variable might be added to say whether the light is enabled:
struct LightProperties {
bool enabled;
vec4 position;
vec3 color;
};
A light can then be represented as a variable of type LightProperties. It will likely be a uniform variable so that its value can be specified on the JavaScript side. Often, there will be multiple lights, represented by an array; for example, to allow for up to four lights:
uniform LightProperties lights[4];
Material properties can also be represented as a struct. Again, the details will vary from one application to another. For example, to allow for diffuse and specular color:
struct MaterialProperties {
vec3 diffuseColor;
vec3 specularColor;
float specularExponent;
};
With these data types in hand, we can write a function to help with the lighting calculation. The following function computes the contribution of one light to the color of a point on a surface. (Some of the parameters could be global variables in the shader program instead.)
vec3 lightingEquation( LightProperties light,
MaterialProperties material,
vec3 eyeCoords, // Eye coordinates for the point.
vec3 N, // Normal vector to the surface.
vec3 V // Direction to viewer.
){
vec3 L, R; // Light direction and reflected light direction.
if ( light.position.w == 0.0 ) { // directional light
L = normalize( light.position.xyz );
}
else { // point light
L = normalize( light.position.xyz/light.position.w - eyeCoords );
}
if (dot(L,N) <= 0.0) { // light does not illuminate the surface
return vec3(0.0);
}
vec3 reflection = dot(L,N) * light.color * material.diffuseColor;
R = -reflect(L,N);
if (dot(R,V) > 0.0) { // ray is reflected toward the the viewer
float factor = pow(dot(R,V),material.specularExponent);
reflection += factor * material.specularColor * light.color;
}
return reflection;
}
Then, assuming that there are four lights, the full calculation of the lighting equation might look like this:
vec3 color = vec3(0.0); // Start with black (all color components zero).
for (int i = 0; i < 4; i++) { // Add in the contribution from light i.
if (lights[i].enabled) { // Light can only contribute color if enabled.
color += lightingEquation( lights[i], material, eyeCoords, normal, viewDirection );
}
}
Two-sided Lighting
The sample program webgl/parametric-function-grapher.html uses GLSL data structures similar to the ones we have just been looking at. It also introduces a few new features. The program draws the graph of a parametric surface. The (x,y,z) coordinates of points on the surface are given by functions of two variables u and v. The definitions of the functions can be input by the user. There is a viewpoint light, but two extra lights have been added in an attempt to provide more even illumination. The graph is considered to have two sides, which are colored yellow and blue. The program can, optionally, show grid lines on the surface. Here’s what the default surface looks like, with grid lines:
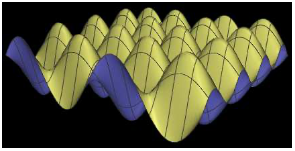
This is an example of two-sided lighting (Subsection 4.2.4). We need two materials, a front material for drawing front-facing polygons and a back material for drawing back-facing polygons. Furthermore, when drawing a back face, we have to reverse the direction of the normal vector, since normal vectors are assumed to point out of the front face.
But when the shader program does lighting calculations, how does it know whether it’s drawing a front face or a back face? That information comes from outside the shader program: The fragment shader has a built-in boolean variable named gl_FrontFacing whose value is set to true before the fragment shader is called, if the shader is working on the front face of a polygon. When doing per-pixel lighting, the fragment shader can check the value of this variable to decide whether to use the front material or the back material in the lighting equation. The sample program has two uniform variables to represent the two materials. It has three lights. The normal vectors and eye coordinates of the point are varying variables. And the normal transformation matrix is also applied in the fragment shader:
uniform MaterialProperties frontMaterial; uniform MaterialProperties backMaterial; uniform LightProperties lights[3]; uniform mat3 normalMatrix; varying vec3 v_normal; varying vec3 v_eyeCoords;
A color for the fragment is computed using these variables and the lightingEquation function shown above:
vec3 normal = normalize( normalMatrix * v_normal );
vec3 viewDirection = normalize( -v_eyeCoords);
vec3 color = vec3(0.0);
for (int i = 0; i < 3; i++) {
if (lights[i].enabled) {
if (gl_FrontFacing) { // Computing color for a front face.
color += lightingEquation( lights[i], frontMaterial, v_eyeCoords,
normal, viewDirection);
}
else { // Computing color for a back face.
color += lightingEquation( lights[i], backMaterial, v_eyeCoords,
-normal, viewDirection);
}
}
}
gl_FragColor = vec4(color,1.0);
Note that in the second call to lightEquation, the normal vector is given as −normal. The negative side reverses the direction of the normal vector for use on a back face.
If you want to use two-sided lighting when doing per-vertex lighting, you have to deal with the fact that gl_FrontFacing is not available in the vertex shader. One option is to compute both a front color and a back color in the vertex shader and pass both values to the fragment shader as varying variables. The fragment shader can then decide which color to use, based on the value of gl_FrontFacing.
There are a few WebGL settings related to two-sided lighting. Ordinarily, WebGL determines the front face of a triangle according to the rule that when the front face is viewed, vertices are listed in counterclockwise order around the triangle. The JavaScript command gl.frontFace(gl.CW) reverses the rule, so that vertices are listed in clockwise order when the front face is viewed. The command gl.frontFace(gl.CCW) restores the default rule.
In some cases, you can be sure that no back faces are visible. This will happen when the objects are closed surfaces seen from the outside, and all the polygons face towards the outside. In such cases, it is wasted effort to draw back faces, since you can be sure that they will be hidden by front faces. The JavaScript command gl.enable(gl.CULL_FACE) tells WebGL to discard polygons without drawing them, based on whether they are front-facing or back-facing. The commands gl.cullFace(gl.BACK) and gl.cullFace(gl.FRONT) determine whether it is back-facing or front-facing polygons that are discarded when CULL_FACE is enabled; the default is back-facing.
The sample program can display a set of grid lines on the surface. As always, drawing two objects at exactly the same depth can cause a problem with the depth test. As we have already seen at the end of Subsection 3.4.1 and in Subsection 5.1.3, OpenGL uses polygon offset to solve the problem. The same solution is available in WebGL. Polygon offset can be turned on with the commands
gl.enable(gl.POLYGON_OFFSET_FILL);
gl.polygonOffset(1,1);
and turned off with
gl.disable(gl.POLYGON_OFFSET_FILL);
In the sample program, polygon offset is turned on while drawing the graph and is turned off while drawing the grid lines.
Moving Lights
In our examples so far, lights have been fixed with respect to the viewer. But some lights, such as the headlights on a car, should move along with an object. And some, such as a street light, should stay in the same position in the world, but changing position in the rendered scene as the point of view changes.
Lighting calculations are done in eye coordinates. When the position of a light is given in object coordinates or in world coordinates, the position must be transformed to eye coordinates, by applying the appropriate modelview transformation. The transformation can’t be done in the shader program, because the modleview matrix in the shader program represents the transformation for the object that is being rendered, and that is almost never the same as the transformation for the light. The solution is to store the light position in eye coordinates. That is, the shader’s uniform variable that represents the position of the light must be set to the position in eye coordinates.
For a light that is fixed with respect to the viewer, the position of the light is already expressed in eye coordinates. For example, the position of a point light that is used as a viewpoint light is (0,0,0), which is the location of the viewer in eye coordinates. For such a light, the appropriate modelview transformation is the identity.
For a light that is at a fixed position in world coordinates, the appropriate modelview transformation is the viewing transformation. The viewing transformation must be applied to the world-coordinate light position to transform it to eye coordinates. In WebGL, the transformation should be applied on the JavaScript side, and the output of the transformation should be sent to a uniform variable in the shader program. Similarly, for a light that moves around in the world, the combined modeling and viewing transform should be applied to the light position on the JavaScript side. The glMatrix library (Subsection 7.1.2) defines the function
vec4.transformMat4( transformedVector, originalVector, matrix );
which can be used to do the transformation. The matrix in the function call will be the modelview transformation matrix. Recall, by the way, that light position is given as a vec4, using homogeneous coordinates. (See Subsection 4.2.3.) Multiplication by the modelview matrix will work for any light, whether directional or point, whose position is represented in this way. Here is a JavaScript function that can be used to set the position:
/* Set the position of a light, in eye coordinates
* @param u_position_loc The uniform variable location for
* the position property of the light.
* @param modelview The modelview matrix that transform object
* coordinates to eye coordinates.
* @param lightPosition The location of the light, in object
* coordinates (a vec4).
*/
function setLightPosition( u_position_loc, modelview, lightPosition ) {
var transformedPosition = new Float32Array(4);
vec4.transformMat4( transformedPosition, lightPosition, modelview );
gl.uniform4fv( u_position_loc, transformedPosition );
}
Remember that the light position, like other light properties, must be set before rendering any geometry that is to be illuminated by the light.
Spotlights
We encountered spotlights in three.js in Subsection 5.1.4. In fact, although I didn’t mention it, spotlights already existed in OpenGL 1.1. Instead of emitting light in all directions, a spotlight emits only a cone of light. A spotlight is a kind of point light. The vertex of the cone is located at the position of the light. The cone points in some direction, called the spot direction. The spot direction is specified as a vector. The size of the cone is specified by a cutoff angle; light is only emitted from the light position in directions whose angle with the spot direction is less than the cutoff angle. Furthermore, for angles less than the cutoff angle, the intensity of the light ray can decrease as the angle between the ray and spot direction increases. The rate at which the intensity decreases is determined by a non-negative number called the spot exponent. The intensity of the ray is given by \( I*c^{s} \) where I is the basic intensity of the light, c is the cosine of the angle between the ray and the spot direction, and s is the spot exponent.
This illustration shows three spotlights shining on a surface; the images are taken from the sample program webgl/spotlights.html:

The cutoff angle for the three spotlights is 30 degrees. In the image on the left, the spot exponent is zero, which means there is no falloff in intensity with increasing angle from the spot direction. For the middle image, the spot exponent is 10, and for the image on the right, it is 20.
Suppose that we want to apply the lighting equation to a spotlight. Consider a point P on a surface. The lighting equation uses a unit vector, L, that points from P towards the light source. For a spotlight, we need a vector that points from the light source towards P; for that we can use −L. Consider the angle between −L and the spot direction. If that angle is greater than the cutoff angle, then P gets no illumination from the spotlight. Otherwise, we can compute the cosine of the angle between −L and the spot direction as the dot product \( -D \cdot L \), where D is a unit vector that points in the spot direction.
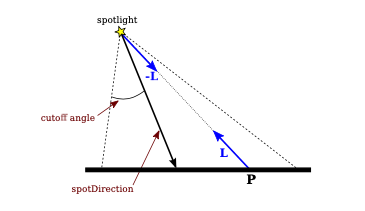
To implement spotlights in GLSL, we can add uniform variables to represent the spot direction, cutoff angle, and spot exponent. My implementation actually uses the cosine of the cutoff angle instead of the angle itself, since I can then compare the cutoff value using the dot product, \( -D \cdot L \), that represents the cosine of the angle between the light ray and the spot direction. The LightProperties struct becomes:
struct LightProperties {
bool enabled;vec4 position;
vec3 color;
vec3 spotDirection;
float spotCosineCutoff;
float spotExponent;
};
With this definition, we can compute the factor \( c^{e} \) that is multiplied by the basic light color to give the effective light intensity of the spotlight at a point on a surface. The following code for the computation is from the fragment shader in the sample program. The value of \( c^{e} \) is assigned to spotFactor:
L = normalize( light.position.xyz/light.position.w - v_eyeCoords );
if (light.spotCosineCutoff > 0.0) { // the light is a spotlight
vec3 D = normalize(light.spotDirection); // unit vector!
float spotCosine = dot(D,-L);
if (spotCosine >= light.spotCosineCutoff) {
spotFactor = pow(spotCosine,light.spotExponent);
}
else { // The point is outside the cone of light from the spotlight.
return vec3(0.0); // The light will add no color to the point.
}
}
// Light intensity will be multiplied by spotFactor
You should try the sample program, and read the source code. Or try the demo in the on-line version of this section, which is similar to the sample program, but with an added option to animate the spotlights.
The spotDirection uniform variable gives the direction of the spotlight in eye coordinates. For a moving spotlight, in addition to transforming the position, we also have to worry about transforming the direction in which the spotlight is facing. The spot direction is a vector, and it transforms in the same way as normal vectors. That is, the same normal transformation matrix that is used to transform normal vectors is also used to transform the spot direction. Here is a JavaScript function that can be used to apply a modelview transformation to a spot direction vector and send the output to the shader program:
/* Set the direction vector of a light, in eye coordinates.
* @param modelview the matrix that does object-to-eye coordinate transforms
* @param u_direction_loc the uniform variable location for the spotDirection
* @param lightDirection the spot direction in object coordinates (a vec3)
*/
function setSpotlightDirection( u_direction_loc, modelview, lightDirection ) {
var normalMatrix = mat3.create();
mat3.normalFromMat4( normalMatrix,modelview );
var transformedDirection = new Float32Array(3);
vec3.transformMat3( transformedDirection, lightDirection, normalMatrix );
gl.uniform3fv( u_direction_loc, transformedDirection );
}
Of course, the position of the spotlight also has to be transformed, as for any moving light.
Light Attenuation
There is one more general property of light to consider: attenuation. This refers to the fact that the amount of illumination from a light source should decrease with increasing distance from the light. Attenuation applies only to point lights, since directional lights are effectively at infinite distance. The correct behavior, according to physics, is that the illumination is proportional to one over the square of the distance. However, that doesn’t usually give good results in computer graphics. In fact, for all of my light sources so far, there has been no attenuation with distance.
OpenGL 1.1 supports attenuation. The light intensity can be multiplied by \( 1.0 / (a + b*d + c*d^{2}) \), where d is the distance to the light source, and a, b, and c are properties of the light. The numbers a, b, and c are called the “constant attenuation,” “linear attenuation,” and “quadratic attenuation” of the light source. By default, a is one, and b and c are zero, which means that there is no attenuation.
Of course, there is no need to implement exactly the same model in your own applications. For example, quadratic attenuation is rarely used. In the next sample program, I use the formula \( 1 / (1 + a*d) \) for the attenuation factor. The attenuation constant a is added as another property of light sources. A value of zero means no attenuation. In the lighting computation, the contribution of a light source to the lighting equation is multiplied by the attenuation factor for the light.
Diskworld 2
The sample program webgl/diskworld-2.html is our final, more complex, example of lighting in WebGL. The basic scene is the same as the three.js example threejs/diskworld-1.html from Subsection 5.1.5, but I have added several lighting effects.
The scene shows a red “car” traveling around the edge of a disk-shaped “world.” In the new version, there is a sun that rotates around the world. The sun is turned off at night, when the sun is below the disk. (Since there are no shadows, if the sun were left on at night, it would shine up through the disk and illuminate objects from below.) At night, the headlights of the car turn on. They are implemented as spotlights that travel along with the car; that is, they are subject to the same modelview transformation that is used on the car. Also at night, a lamp in the center of the world is turned on. Light attenuation is used for the lamp, so that its illumination is weak except for objects that are close to the lamp. Finally, there is dim viewpoint light that is always on, to make sure that nothing is ever in absolute darkness. Here is a night scene from the program, in which you can see how the headlights illuminate the road and the trees, and you can probably see that the illumination from the lamp is stronger closer to the lamp:

But you should run the program to see it in action! And read the source code to see how it’s done.
My diskworld example uses per-pixel lighting, which gives much better results than per-vertex lighting, especially for spotlights. However, with multiple lights, spotlights, and attenuation, per-pixel lighting requires a lot of uniform variables in the fragment shader — possibly more than are supported in some implementations. (See Subsection 6.3.7 for information about limitations in shader programs.) That’s not really serious for a sample program in a textbook; it just means that the example won’t work in some browsers on some devices. But for more serious applications, an alternative approach would be desirable, hopefully better than simply moving the calculation to the vertex shader. One option is to use a multi-pass algorithm in which the scene is rendered several times, with each pass doing the lighting calculation for a smaller number of lights.
(In fact, even on my very old computer, which advertises a limit of 4096 uniform vectors in the fragment shader, I had a problem trying to use five lights in the diskworld example. With five lights, I got weird color errors. For example, the red or green color component might be completely missing from the image. I solved the problem by using the same light for the sun and the lamp, which are never both on at the same time. The program worked fine with four lights. Admittedly, I have an eight-year old computer with a somewhat buggy GPU, but this shows some of the issues that can come up for certain WebGL programs on certain devices.)


